基于模糊控制的光伏微电网复合储能控制策略优化研究
何飞帆,高文根,於 跃
安徽工程大学 电气工程学院,安徽 芜湖 241000
1 引 言
新型可再生能源已然成为解决能源危机的最佳手段,伴随着国家对低碳生活的要求和政策,以光能、风能和水能为代表的一系列可再生能源在电网中所占比例持续增加,但新能源发电受天气、环境和温度等各方面影响,导致并网发电功率波动较大,给电网调度方面带来诸多困难[1-2]。为了缓解这一棘手问题,以光伏发电为例,现有的大型光伏电站一般都通过对光伏发电量进行预测并规划发电计划,再通过竞标的形式获得并网权。即使如此,由于大型光伏电站的容量很大,向外输电的工程中存在很多问题,因此在规划与实际情况出现较大偏差或系统故障等情况时,会出现弃光现象,严重时甚至会引起电网解列[3-4]。
复合储能系统主要用于平抑系统中的功率波动,补偿功率缺额[5-6]。复合储能系统中的功率分配问题一直是业内研究的热点,在文献[7]中提出一种在储能系统独立运行时,根据储能元件SOC设计模糊控制器并通过模糊算法动态的调节下垂系数,但该论文将充放电过程在长周期内分开讨论,未能考虑到短周期内储能系统的充放转换;文献[8]根据各时间段电价和用电需求侧的变化,从宏观方面设计了一种针对光氢储微网的调度方案,但此方案未考虑新能源发电的不稳定性所带来的影响;文献[9]提出利用模糊控制和加权移动平均滤波算法对权重系数和滤波带宽进行实时调整,以此来达到自动调整储能系统SOC的目的,但由于其控制方式为实时控制,可能会造成储能系统充放次数频繁,缩短储能系统设备的使用寿命;文献[10]提出一种摒弃滤波方式,只根据超级电容SOC大小分配能量的方法,以此来消除使用滤波器带来的功率波动,但该方法更容易造成单个储能元件在长周期内频繁充放电,加速其元件损坏,缩短储能元件使用寿命。
文献[11]提出了一种基于能量预测的光伏微电网复合储能控制策略方法,首先在光伏和负载能量预测的基础上制定并网调度计划,再根据实际并网调度与计划并网调度的误差对储能系统进行调控,但该研究将能量差额平均分配给储能系统,没有考虑微电网功率波动的非线性特性。本文在该文献的控制方法基础上,综合考虑微电网功率波动的非线性特性,在预测能量与实际能量的误差分配环节加入模糊控制器,通过模糊控制对误差进行实时的分配以此来防止储能系统SOC越限,并实现蓄电池与超级电容的参考功率优化分配。仿真结果表明,经过模糊控制后的储能元件输出功率符合其特性,在长时间尺度上,实际并网功率能准确跟踪并网调度,蓄电池SOC保持在百分之五十左右波动,避免储能系统过充(过放)问题,提高了复合储能系统的鲁棒性。
2 含复合储能的光伏微电网结构
2.1 微电网简介
微电网(Micro-grid)又可称为微网,其结构是由电网和分布式发电单元组成电源,发电单元通过能量转换器将电量输入到母线,同时再由母线通过转换器将电能输送到用户。当发生特殊情况时,微电网不仅可以选择并网运行,还可以选择脱离电网进行离网运行。因此,微电网不仅可以解决大规模的分布式发电单元并联接入问题,而且还可以充分发挥其优势,在面对大规模紧急情况中发挥充分作用。微电网将从根本上改变传统的应对负荷增长的方式,在降低能耗、提高电力系统可靠性和灵活性方面具有巨大潜力[12]。
微电网可以根据其运行方式的不同分为以下两种模式:并网模式和离网模式。并网模式下的微电网由发电单元、负荷单元、控制单元、储能单元以及电网所组成。当微电网对电网的渗透率较低的情况下时,电网可以作为备用电源填补能量。但由于微电网内部的电源和负荷具有不确定性,故当电网中的微电网数量逐渐增大时,将会影响电网的稳定性。离网模式下的微电网失去了电网的支撑,其电源与负荷的功率平衡将由微电网自身来调节。但由于微电网体量较小,很容易引发电压过小、超频等现象,从而导致系统失稳。加入了新型可再生能源的微电网由于可再生能源受到环境与地理位置等因素的影响,其发电量具有随机性。同时,由于微电网中的负荷也具有随机性,因此由储能系统对微电网功率调节成为平衡源荷功率的重要途径。
2.2 复合储能系统组成
当电源提供能量不足以满足负载消耗时,储能系统放电补足空缺;同理,当电源提供能量大于负载消耗时,储能系统吸收能量并储存。储能系统可以按照其功能划分为两类,即功率型储能与能量型储能(如超级电容和磷酸铁锂电池等)。功率型储能主要是满足微电网系统功率调节需求,要求储能电池功率密度高、响应速度快、允许频繁充放电;能量型储能主要是微电网系统的能量吞吐需求,要求储能电池能量密度大[13]。本文选择以超级电容和磷酸铁锂电池所组成的复合储能系统(表1),超级电容作为功率型储能电池具有响应时间快,响应时间短,可频繁充放电等特点,可用于微电网的瞬态功率调整,维持电压和频率的稳定;磷酸铁锂电池作为能量型储能具有价格便宜、功率密度大、响应速度与超级电容形成互补等特点,主要用于满足微电网各单元功率调节需求。

表1 复合储能系统两种电池功能划分Table 1 Function division of two kinds of batteries in composite energy storage system
2.3 光伏-储能-负荷微电网结构
光伏微电网系统由光伏发电单元、储能单元和负荷三部分组成,其结构可根据不同的能量转换方式分为直流型、交流型和混合型。直流型微电网是通过直流母线将电源、储能和负载三者相连,然后通过直流母线直接进行能量转换;交流型微电网采用交流总线,实现电源、储能、负载互联和能量转换;混合型微电网采用内部直流总线将产生的直流电通过AC/DC逆变器转化为交流电输出到交流母线中。本文采用并网模式下的交流型光伏微电网,相对于直流型和混合型而言,交流型投入成本更低,结构相对简单,性价比更高。如图1所示,分布式光伏发电单元由逆变器将产生的直流电逆变为交流电输出到交流母线;直流母线通过电源转换系统(Power Conversion System,PCS)连接到交流母线,交流母线通过耦合(Point of Common Coupling,PCC)开关连接到电源变压器,然后通过变压器连接到电网。微电网通过PCC点与电网交换电能,交流和直流总线通过PCS交换电能。通过控制混合储能能量的放电,稳定直流侧光伏发电和交流侧负载功率的波动。复合储能单元由超级电容和蓄电池组成,通过PCS并联到交流母线,放电状态下通过功率变换系统将蓄电池中的直流电转换成交流电输出到交流母线;充电状态下通过功率变换系统将交流母线中的交流电转换为直流电储存在蓄电池当中;负载直接并联到交流母线当中。

图1 光伏、储能、负荷微电网结构图Fig.1 Structure diagram of photovoltaic,energy storage and load microgrid
光伏微电网中的各单元关系如图1所示,Ppvi为光伏微电网各支路发电单元,其中i∈[1,n],PLj为负荷单元用电功率,其中j∈[1,m],Pg为实际并网功率,Pc为超级电容输出功率,Pb为蓄电池输出功率;Ppv为各支路光伏发电功率之和,其对应的光伏预测值为Ppvp;PL为光伏微电网中负荷元件消耗的总功率,其对应的负荷预测值为PLp;同时,记光-荷的预测值之和为Ppp,其实际值为Pp。
3 基于能量预测与跟踪并网调度的复合储能控制策略
3.1 光伏微电网中复合储能系统的控制方法
此方案首先根据光伏发电量的预测值和负荷的预测值,计算出以一天(1 d)为周期的并网功率预测值;其次,获取并网计划调度曲线,再以小时(h)为周期更新能量预测值反馈到并网计划,通过控制储能系统进行充放电来平抑功率波动误差;最后,实现光伏微电网跟踪并网调度计划的控制目标。
由于并网调度计划与预测值的误差受到环境、天气等各种不确定因素的影响,所以其数值处于实时波动的状态。为了减少储能系统充放次数,针对并网调度计划与预测值的误差值设置一个误差带。当并网调度计划与预测值的差值没有超过误差取值范围时,储能系统不工作;当误差超过允许误差且实际并网功率大于调度并网功率时,储能系统进行充电吸收多余能量;同理,当误差超过允许误差且实际并网功率小于调度并网功率时,储能系统放电补偿并网功率。
假设交直流能量转化中不存在损耗,则令光伏微电网跟踪电网调度的计划并网功率为Ps,为了实现电网调度目标,需要跟踪计划并网功率输出,通过控制复合储能输出功率来平抑功率偏差ΔP,则有:
Pg=PPVp+PLp
ΔP=PS-Pp=PS-PPV-PL
为了实现并网调度目标,有必要跟踪规划的并网发电量,并通过控制混合储能装置的输出功率来稳定功率偏差,然后存在:
PH=PS-PG=PS-PL+PPV
当PH>0时,表示实际并网功率大于计划并网功率,此时储能系统应通过充电来吸收多余的电量;当PH=0时,表示实际并网功率等于计划并网功率,此时储能系统不工作;当PH<0时,实际并网功率小于计划并网功率,控制储能系统放电补足偏差。
3.2 光伏微电网复合储能系统控制流程
基于能量预测与并网调度计划的复合储能控制方案如图2所示。根据光伏和负荷一天的预测值,结合蓄能系统状态来制定并网调度计划,电网根据调度计划进行放电。再将每日预测值和实际电网调度总量分解成以小时为周期,再将得到预测值与实际调度值做对比,得到以小时为周期的差值ΔEp,h,最后由储能系统进行充放电对差值平抑补缺。与此同时,将差值ΔEp,h以小时为周期滚动预测下一个周期的能量状态,实际并网根据所得差值进行补缺,以此来修正日预测误差获得更加准确的储能功率修正参考值,达到更佳的控制目标。图2中Td表示为以1 d为周期;Th表示为以小时为周期;Ep,d表示为1 d的光伏与负荷能量预测值;Ep,h表示为以小时为周期的光伏与负荷能量预测值;ΔEp,h为以小时为周期实际电网输出值与光-荷能量预测值的误差。

图2 光伏微电网复合储能系统控制流程Fig. 2 Control process of photovoltaic microgrid composite energy storage system
3.3 跟踪并网调度的复合储能系统能量控制策略
由图2可知,并网调度1 d内(Td)能量预测值为
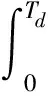
1 h(Th)内的并网能量预测值为
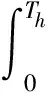
实际需要的并网能量为
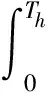
根据光伏微电网能量预测值和实际并网能量值,预计未来调度周期内的产生的能量误差为
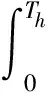
在文献[11]中,针对能量差额ΔEp,采用按时间平均分配到调度周期的方式,即:
(1)
式(1)中,kc为超级电容分配系数,kb为蓄电池分配系数。根据调度周期Td和分配系数,将能量差额平均分配给储能系统。由于采用均值算法没有考虑微电网系统功率波动的非线性特性,尤其是蓄电池的SOC非线性特性,可能会导致储能系统出现过充或过放现象,从而造成储能系统元件的损坏,例如:当储能系统SOC较低时,系统仍处于放电状态,由于线性算法的缘故使得储能元件无法根据自身状态来调整放电量,从而导致储能元件产生过放现象而退出系统;同理,当储能系统SOC较高时,系统仍处于充电状态,由于无法自动调整充电量,从而导致储能元件产生过充以至于导致微电网弃光现象的产生。故在此基础上加入模糊控制器,在考虑储能元件SOC状态的同时,对功率修正系数进行实时调控。
4 模糊控制优化的储能系统控制策略
4.1 模糊控制在复合储能系统上的应用
当实际并网调度与光-荷预测值出现差值时,需要储能系统介入平抑或补充差额。由于超级电容和蓄电池组成的储能系统本身具有容量限制,所以必须要考虑储能元件本身的荷电状态。
为了保证储能元件处于安全运行的状态,本文提出了一种以模糊控制为基础,可以实时监控并修正超级电容和蓄电池功率参考值的系统,更适合于解决系统运行过程中的非线性问题。
模糊控制流程如图3所示:首先,确定输入输出物理量;其次,确定模糊子集的隶属函数并制定模糊控制规则;最后,将得到的模糊值通过清晰化处理得到输出清晰量。

图3 模糊控制策略设计流程Fig. 3 Design process of fuzzy control strategy
加入模糊控制的作用:当储能元件容量即将到达限定容量,储能元件依旧保持充电或放电状态时,适当的调整功率参考值,避免储能元件因为过充或过放而造成损坏,提高储能系统的使用寿命。
4.2 复合储能系统模糊控制策略
在运用模糊控制之前,需要先表示出各储能元件的SOC值以及功率充放状态。由式(1)可知,蓄电池分配系数和超级电容分配系数互补,因此此处取蓄电池为例。
在应用模糊控制之前,需要先将蓄电池有功功率输出和荷电状态SOC进行归一化处理,蓄电池SOC归一化方程表示如下[14]:
其中,Sb,ref为蓄电池SOC的期望值,εb(t)的论域为[-1,1],取极端值说明:当εb(t)=-1时,表示蓄电池处于枯竭状态;当εb(t)=1时,表示蓄电池处于饱和状态。
有功功率参考值隶属度表示如下[15]:

目前,确定隶属度函数的常用方法有多种,本文采用最常用的专家经验法,根据专家实际经验给出的模糊信息,初步确定粗略的隶属函数,再进行多次试验,根据实际效果进行修正和调整隶属函数。
如图4所示,将εb(t)和ηb(t)作为两个输入连接到模糊控制器两个输入接口,取两者论域为[-1,1],其输入模糊集合表示为{NB,NS,ZO,PS,PB},分别代表储能系统中蓄电池的SOC含量为:低、较低、适中、较高、高。其模糊控制器输出值为功率修正值,记为kb(t),将其离散论域定义为[-1,-0.6,-0.3,0,0.3,0.6,1],模糊子集为[NB,NM,NS,ZE,PS,PM,PB]。
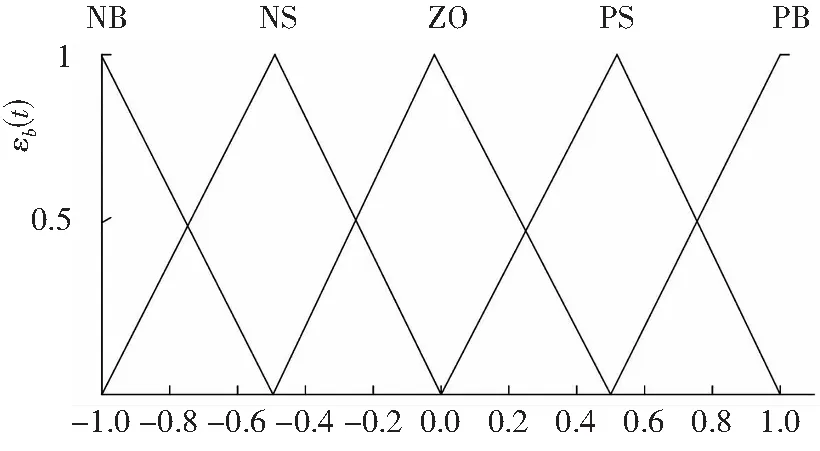
图4 蓄电池输入隶属度函数Fig. 4 Battery input membership function
本文的模糊规则主要根据以下几条原则设计:当蓄电池的SOC含量较小,且蓄电池放电功率仍处于较大时,则减小有功功率输出值,避免过放现象的产生;当蓄电池SOC处于中间值时,按照功率参考值进行补偿;当蓄电池SOC较大时,而蓄电池仍处于充电状态,则减小有功功率输入值,避免过充现象的产生。根据以上理论,得出输入隶属函数(图4)和输出隶属函数(图5)。
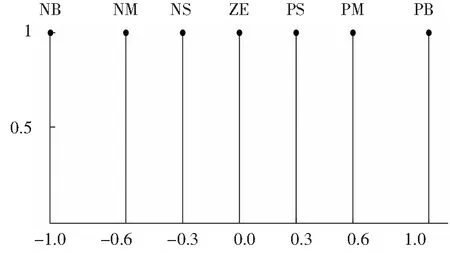
图5 蓄电池输出隶属度函数Fig. 5 Battery output membership function
模糊控制表如表2所示,选取一条加以说明:

表2 控制规则表Table 2 Control rules
Ifεb(t)is ZO andηb(t)is ZO,thenkb(t) is ZE.
规则表明:当蓄电池中SOC含量与参考值含量相差适中(ZO),且蓄电池有功功率参考值与有功功率实际值相差适中时(ZO),此时蓄电池修正系数输出为0(ZE)。除此以外,考虑蓄电池本身特性,当蓄电池荷电状态处于适中范围时,可适当增大其充电或放电功率。
由于得到的输出值为模糊变量,因此需要进行清晰化处理:清晰化计算通常有加权平均法(重心法),最大隶属度法,和中位数法等。本文采用重心法对输出的模糊集合进行清晰化处理,得到实时功率修正数据kb(t),从而得到储能设备功率修正值为
4.3 模糊控制下的复合储能系统能量调控
根据文献[11]可知:工作状态下,蓄电池放电/充电的SOC的表达公式为
(2)
(3)
其中,T为SOC更新周期;Pfa为放电功率;Pch为充电功率;μc为充电效率;Sn为额定容量;μf为放电效率。
将储能设备功率修正值加入式(2)中,得到在放电状态下,蓄电池的放电有功功率参考值为
将储能设备功率修正值加入式(3)中,得到在充电状态下,蓄电池的充电有功功率参考值为
同时,储能元件的充放电功率应该保持在其元件规定的范围内。因此,为了保证储能元件的充放功率保持在允许的范围内,应对其功率加以约束条件来保证系统的安全:
5 仿真分析
基于上述理论,本文在仿真软件MATLAB/Simulink中搭建模型并进行仿真分析。在本文的算例中,储能元件的允许充电(放电)深度设为0%~100%,SOC初始值设定为50%,仿真时间尺度为24 h,光伏能量预测和负荷能量预测以1 h为周期滚动更新。仿真参数如表3所示,储能元件容量配置方案如表4所示。

表3 仿真参数Tabel 3 Simulation parameters

表4 储能容量配置方案Table 4 Configuration scheme of energy storage capacity
通过仿真验证复合储能控制策略的有效性,得到超级电容与蓄电池的功率如图6所示,超级电容充放次数大于蓄电池充放次数,蓄电池的充放功率大于超级电容,符合超级电容和蓄电池功率特性。
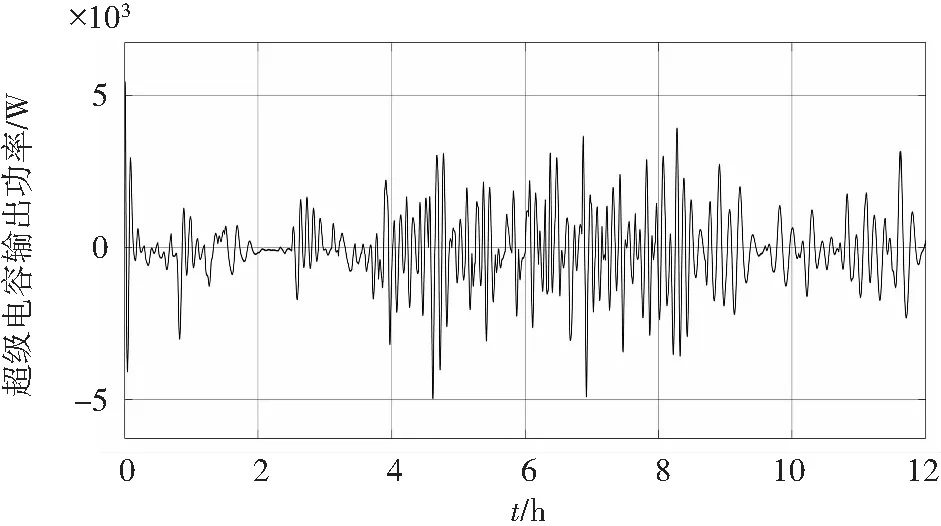
图6 优化后的超级电容与蓄电池功率曲线Fig. 6 Optimized supercapacitor and battery power curves
由图7可知,光伏微电网实际并网功率曲线Pg能够跟踪并网调度曲线Ps。且由于超级电容由于本身元件的物理特性,使其响应时间更短,可进行频繁的充放电,因此利用低通滤波器将波动功率中分解后的高频分量由超级电容平抑;由于蓄电池输出功率缓慢,承担功率较大,因此可用来补偿波动功率中的低频分量。
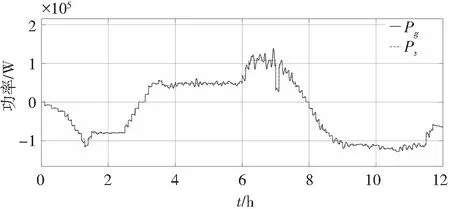
图7 实际并网功率跟踪并网调度曲线Fig. 7 Actual grid-connected power tracking grid-connected dispatching curve
图8为1 d时间内负荷功率变化图。以蓄电池为例,为验证模糊控制对SOC控制的时效性和调节的有效性,图9为蓄电池未经过模糊控制的SOC变化曲线,图10为蓄电池经过模糊控制优化后的SOC变化曲线,图11为蓄电池经过模糊控制时的功率修正曲线。

图8 负荷功率曲线Fig. 8 Load power curve
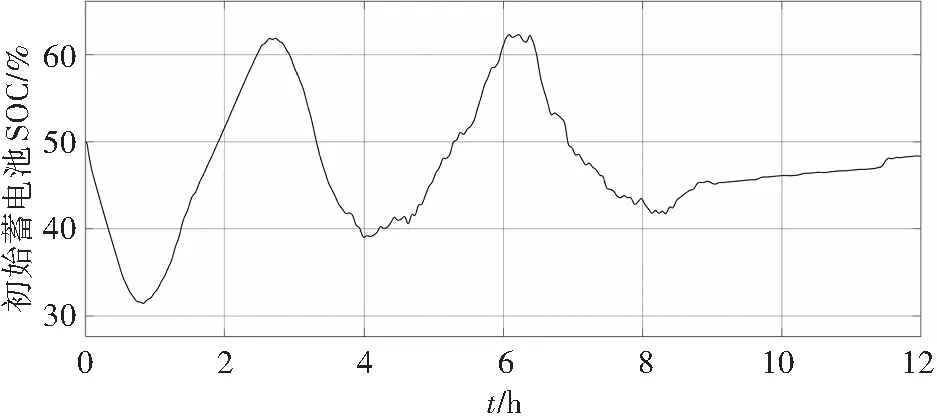
图9 优化前蓄电池SOC变化曲线Fig. 9 Change curve of battery SOC before optimization

图10 优化后的变化曲线Fig.10 Change curve of battery SOC after optimization
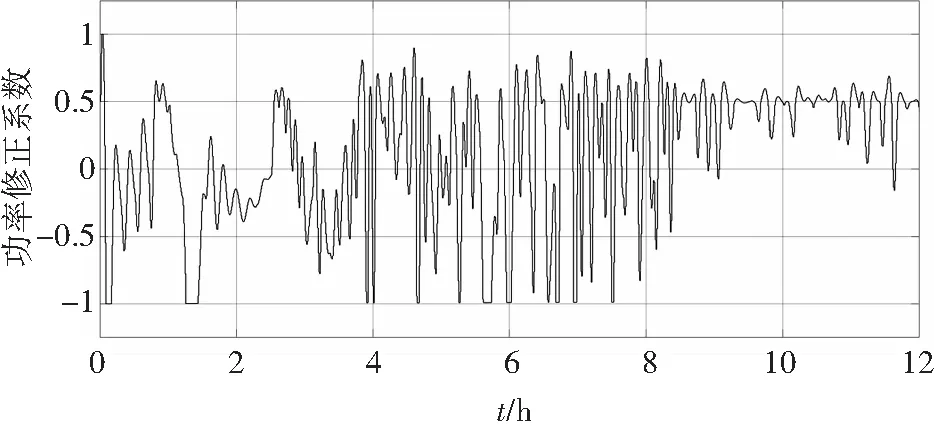
图11 蓄电池功率修改系数Fig.11 Modification factor of battery power
由图10可知,模糊控制下的蓄电池SOC值在50%左右波动,当蓄电池SOC达到设定的敏感区域时能够及时的进行功率修正,使得SOC保持在合理的位置,防止蓄电池过充过放。
6 结 论
选择了一种以能量预测为基础,跟踪并网调度的复合储能控制策略,此策略实现了在更长时间尺度上稳定响应系统的控制需求。在此储能控制控制策略的基础上进行优化,利用模糊算法对非线性问题处理优势,在储能元件功率分配的情况中加入模糊控制器。兼顾考虑储能电池SOC的非线性特性,设计微电网预测能量与实际并网能量的差额分配算法,对储能系统有功功率参考值进行实时修正,从而达到调节储能系统SOC的效果。实现在长时间尺度中,实际并网功率能准确跟踪并网调度的情况下,储能元件不会产生过充或过放的情况,降低了储能元件的损坏率,提高了复合储能系统运行的安全稳定性能,延长了储能系统的使用寿命。仿真结果表明,与优化前的控制策略相比,在相同工况下优化后的控制策略使蓄电池SOC波动范围缩小15.6%,一直保持在40%~60%之间波动。

