常数变易法教学研究

旷雨阳, 李兴华, 王太荣

(贵州省安顺学院 数计学院, 贵州 安顺 561000)

0 引 言

研究非齐次线性微分方程的通解方法很多,如比较系数法、拉普拉斯变换法及其降阶法,本文所研究的常数变易法也是解非齐次线性微分方程通解的一种常用方法[1]。

常数变易法本质上是一种变量替换的思想,通过这种变量替换,可以将不容易直接利用初等积分法求解的复杂方程,转化成已知的、可求解的方程类型,进而求出原方程的通解[2]。因此它除了能够对一阶线性常微分方程进行求解以外,在其他类型的微分方程求解中也同样能够得到良好的应用[3]。

因此常数变易法在微分方程中应用很广,甚至在计算数学、工程科学等领域中应用甚广。张琬等通过常数变易法构造了一个求解非线性系统逼近的迭代过程来消除长期项[4];王敏利用常数变易法与变系数思想构出了常数替换法,利用常数替换法研究了几种周期激励下多频耦合动力系统的近似解析解[5];翟俊杰借助Lyapunov函数法和常数变易法研究了对互联车辆系统在脉冲作用下的稳定性[6];Douglas R利用常数变易法分别研究了一阶h差分方程的Ulam稳定性和二阶h差分方程Hyers-Ulam稳定性[7];Cǎruau Vasile利用常数变易法解决了具有不同形式P(x)的自由项n阶常系数线性微分方程的特解[8];Al Hallak M等用常数变易法讨论了强耦合情形下的暖膨胀和通货膨胀[9];Xuejun Yi等利用常数变易法研究Duffing型振荡器系统的全局渐近同步[10]。因此综上所述,常数变易法在实际问题中应用很广,值得学习与进一步研究探讨。

1 预备知识

y0(n-1),这里x0,y0,y0(1),…,y0(n-1)是给定的n+1个常数。满足初值条件的解称为微分方程的特解。

定义1.3:如果一个n×n矩阵的每一列都是线性微分方程组x′=A(t)x的解,就称这个矩阵为x′=A(t)x的解矩阵。它的列在a≤t≤b上是线性无关的解矩阵称为在a≤t≤b上的x′=A(t)x的基解矩阵。其中A(t)是n×n矩阵,x是n维列向量。

性质1.4(指数矩阵的性质):如果矩阵A,B是可交换的,即AB=BA,则exp(A+B)=expAexpB;对于任何矩阵A,(expA)-1存在,且(expA)-1=exp(-A)。

定理1.5(克莱姆法则):一个含有n个未知量n个方程的线性方程组

2 常数变易法在求解常微分方程中的应用研究

2.1 常数变易法在求解一阶线性微分方程中的应用

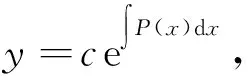
(2.1.1)

对此式微分之,得到:

(2.1.2)

将(2.1.1),(2.1.2)代入原方程得

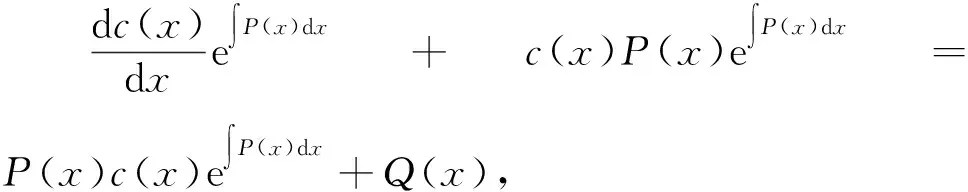
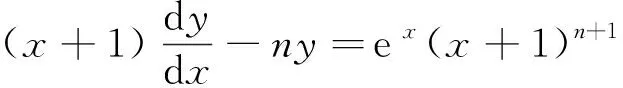
①

②

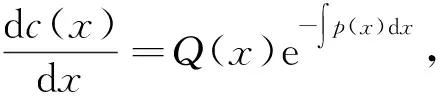
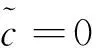
2.2 常数变易法在求解高阶线性微分方程中的应用

设正规形n阶非齐次线性微分方程为

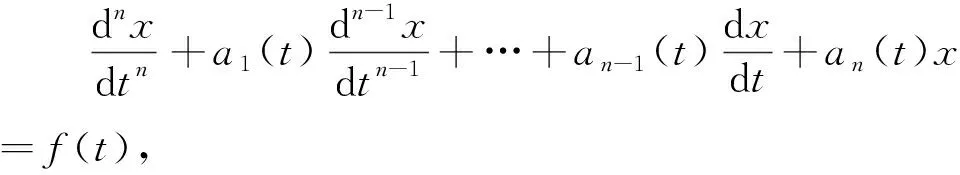
(2.2.1)

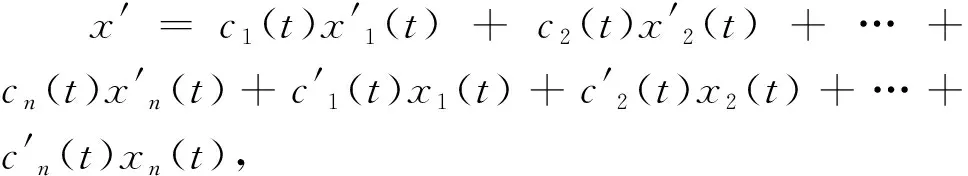
(2.2.2)1

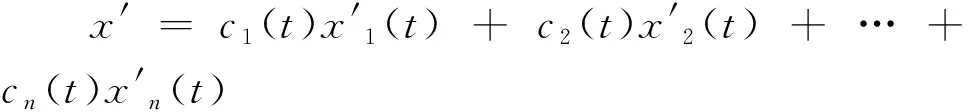
(2.2.3)1

(2.2.2)2

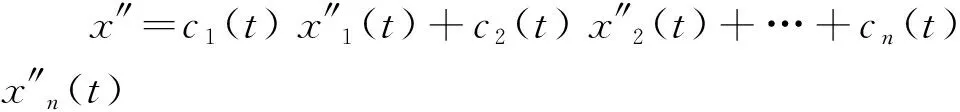
(2.2.3)2

继续上面做法,在最后一次得到第n-1个条件

(2.2.2)n-1

和表达式

x(n-1)=c1(t)x1(n-1)(t)+c2(t)x2(n-1)(t)+…+cn(t)xn(n-1)(t)

(2.2.3)n-1

最后,式(2.2.3)n-1对t微分得到

(2.2.3)n

现将式(2.2.1),式(2.2.3)1,式(2.2.3)2,…,式(2.2.3)n代入原方程,并注意到x1(t),x2(t),…,xn(t)是齐次线性微分方程的解,得到

(2.2.2)n

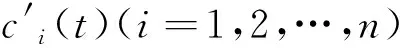
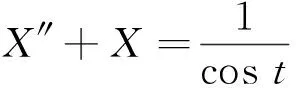
解:对应齐次微分方程为X″+X=0,特征方程为λ2+1=0,特征根为λ1,2=±i,因此对应齐次微分方程的基本解组为x1(t)=cost,x2(t)=sint,因此齐次微分方程通解为x=c1cost+c2sint,应用常数变易法,令c1=c1(t),c2=c2(t),即x=c1(t)cost+

c2(t)sint。

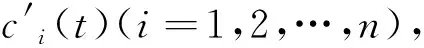
从此原方程通解可以看出,它是由两项迭加而成的,第一项是相应线性齐次微分方程的通解;第二项是线性非齐次微分方程的一个特解(令所有γi=0得此解)。由此便得结论:高阶线性非齐次方程的通解,等于它的相应线性齐次方程的通解与它的一个特解之和。

2.3 常数变易法在求解线性微分方程组中的应用

设非齐次线性微分方程组x′=A(t)x+f(t),其中A(t)是区间[a,b]上的n×n连续矩阵,f(t)是区间[a,b]上的n维连续列向量,x为n维列向量。

若f(t)=0,则原方程组化为齐次线性微分方程组x′=A(t)x,设Φ(t)是齐次线性微分方程组的基解矩阵,则齐次线性微分方程组的通解为x=Φ(t)C,其中C是任意常数列向量,令C=C(t),从而X=Φ(t)C(t)是原方程组的解,这里C(t)为待定的向量函数,将X=Φ(t)C(t)代入原方程组得

Φ′(t)C(t)+Φ(t)C′(t)=A(t)Φ(t)C(t)+f(t)

(2.3.1)

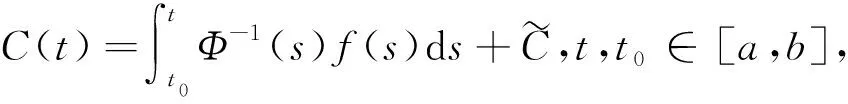
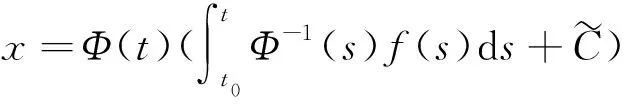
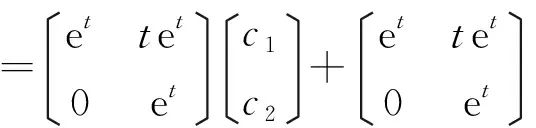
这里c1,c2为任意常数。

教学小结:求解非齐次线性微分方程组的一般步骤为(1)求出原线性微分方程组的相应齐次线性微分方程的基解矩阵;(2)常数变易,作变换C=C(t),把原方程化为Φ(t)C′(t)=f(t),积分后,将之代入X=Φ(t)C(t)中,就得到原方程组的通解。

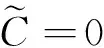
教学总结:从上述用常数变易法求解三类微分方程的过程可以看出,首先都是要求解对应齐次线性微分方程(组)的通解,再常数变易法,令C=C(t)(或ci=ci(t)),求出C(t)(或ci(t)),回代对应的线性齐次微分方程(组)通解中的作常数变易法的C(t)(或ci(t))后,就得到原微分方程(组)的通解,故此三类线性微分方程(组)常数变易法解题步骤思路都是一致的。且此三类线性微分方程(组)的通解都是由相应线性齐次方程(组)的通解与它的一个特解之和。