非均匀采样非线性多智能体系统无模型控制
李昊哲,王宏伟,2*,郭明霄,杨仕旗
(1. 新疆大学电气工程学院,新疆 乌鲁木齐 830047;2. 大连理工大学控制科学与工程学院,辽宁 大连 116024)
1 引言
随着计算机技术、通信技术和网络技术的发展,在解决大型复杂的实际问题时,可采用多智能体间的合作机制,代替单个系统获得更好的工作效率和性能。其中,一致性问题是多智能体系统控制的基础,基本思想是为每个智能体设计控制协议,通过局部信息交互构成网络系统,因此控制协议的设计仅取决于本地和邻居的信息,以便所有智能体都能收敛于相同的轨迹[1]。由于多智能体系统在分布式协同控制和群体决策方面的优势,现已被广泛应用于诸多领域:如卫星编队的姿态控制、无人机密集编队飞行控制、自主水下机器人导航、移动机器人编队控制和智慧工厂等[2-6]。对于线性的多智能体系统,为了避免全局状态信息的使用,文献[7]提出了一种完全分布式的自适应控制方法。文献[8,9]利用投影算法和确定性等价原理,研究一类带有耦合参数的非线性多智能体系统的控制问题。文献[10,11]讨论了网络拓扑中存在虚拟者领导者情况下的一致性跟踪问题。文献[12-14]分别研究了时变拓扑情况下的一致性跟踪问题。文献[15]考虑了具有输出量化和通信延迟情况下的一致性跟踪问题。
分析上述文献发现,目前多智能体系统一致性控制的相关成果,大多是在确定的系统模型上展开的研究。然而,实际的多智能体系统却很难建立精确的数学模型,且往往是异构的,非线性的。因此,数据驱动控制被广泛应用在多智能体领域。Chen等提出分布式合作学习控制方法解决一组未知非线性系统的跟踪控制问题[16,17]。Milad等提出了分布式自适应神经网络控制策略[18]。虽然这些控制方法可以通过神经网络来逼近每个智能体未知的非线性部分,无需建立精确的数学模型。但是,却需要大量的I/O数据来训练神经网络,以获得对未知非线性部分更好的逼近效果。针对神经网络控制需要大量训练数据的缺点,文献[19]利用动态线性化技术,提出了一种分布式无模式自适应控制(MFAC)方法,解决非线性多智能体系统的一致性跟踪控制问题。针对具有周期运行特点的非线性多智能体,文献[20]研究了自适应迭代学习控制策略。
然而,上述数据驱动控制策略大多是由均匀刷新的零阶保持器实现。但是由于传感器设备受到物理、机械等因素限制,以及在网络控制系统中控制信号的传输存在丢失和延时现象,因此控制信号需使用非均匀刷新的方案,即在固定的框架周期内多次刷新,以获得较好的控制效果。非均匀多采样率系统在增加控制系统复杂性的同时,提高了系统的控制性能。当系统的输入信号非均匀周期刷新,输出信号周期采样,是一类特殊的非均匀采样系统。针对此类系统,文献[21]将非均匀采样系统分解为多个子系统,提出了多模型自校正控制方法。文献[22]基于最优控制原理对非均匀采样系统进行了研究。为解决一类非均匀采样非线性系统的控制问题,文献[23]提出了一种无模型自适应控制策略。但是这些方法仅适用于单一系统的控制,并不适用于多智能体系统的控制。主要困难在于:①已有方法不能很好解决非均匀采样多智能体系统控制的一致性问题,即所有智能体输出跟踪误差一致有界;②多智能体的模型信息是未知的,不同智能体的动力学信息往往是异构的。
针对以上问题,本文主要研究了一类输入非均匀刷新和输出周期采样的非线性多智能体系统一致性跟踪控制问题。首先,利用提升变量技术将未知的非均匀采样非线性系统,转化为基于当前工作点处的紧格式动态线性化(CFDL)数据模型;然后,利用输入和输出数据对(CFDL)数据模型中的伪雅可比向量进行参数估计;在此基础上,引入虚拟领导者产生期望轨迹,并对每个智能体设计分布式无模型自适应控制策略,实现对参考信号的一致性跟踪;另外,本文还对控制算法的收敛性能,以及控制器参数选择等进行了分析,并给出跟踪误差收敛的必要条件。
2 预备知识和问题的描述
2.1 符号说明
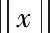
2.2 代数图论
对于q个智能体构成的多智能体系统可用有向图G(V,E,A)表示,q个智能体可视为q个节点,V={v1,v2,…,vq}表示节点集合,每个节点表示一个智能体系统。E⊆V×V表示边集合,其中E={e1,e2,…,en},有向边(vi,vj)∈E表示节点i可以接收到节点j的信息,信息传递方向不可逆[24]。A=[aij]q×q是权值邻接矩阵,若(vi,vj)∈E,则aij>0,否则,aij=0。度矩阵被定义为D=diag{d1,…,dq},其中图G的Laplacian矩阵L[lij]∈Rq×q被定义为L=D-A。
2.3 问题的描述
考虑异构多智能体控制系统是由q个智能体组成的,其结构如图1所示,其中Hτ是非均匀保持器,刷新间隔是{τ1,τ2,…,τl},作用是将控制器产生的离散信号ui(kT+tl)(t1=0,tl=tl-1+τl=τ1+,…,τl,l=1,…,p)经过刷新产生连续的控制信号ui(t)。

图1 跟随者智能体分布式控制方案

其中,控制信号ui(t)为

(1)

(2)
其中,xi(t)∈Rn是智能体i的状态变量,ui(t)∈R1和yi(t)∈R1分别是智能体i的输入和输出变量。
在输入数据ui(kT+tl)和输出数据yi(kT)是可观测的情况下,令xi(kT+T)是(2)式离散方程的解,其离散状态方程为

(3)

∈Rp×1,i=1,2,…,q
(4)
对于(3)式的非均匀采样离散系统,可采用多模型形式表示。首先考虑一个线性的非均匀采样系统,其状态空间方程如下

(5)
其中xi(t)∈Rn,ui(t)∈R1和yi(t)∈R1分别是状态,控制信号和输出信号。Aci,Bci和Ci是适当维数的参数矩阵。
参考文献[21],对式(5)进行离散化

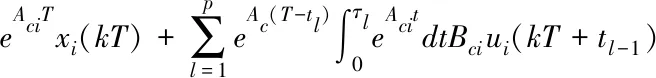

(6)
yi(kT)=Cixi(kT)
(7)
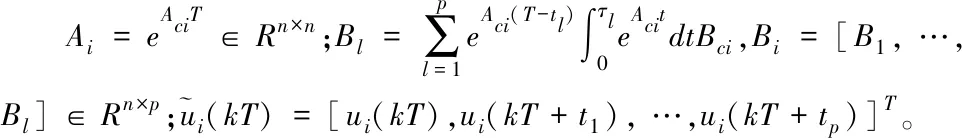
然后,引入前移算子z,zxi(kT)=xi(kT+T),则式(7)表示为

(8)
其中
a(z)=z-ndet[zIn-Ai]=1+a1z-1+a2z-2+…anz-n,aj∈R1;
b1(z)=Ciz-nadj[zIn-Ai]B1=b10+b11z-1+b12z-2+…blnz-n,b1j∈R1,b10=0,bl(z)=Ciz-nadj[zIn-Ai]Bl=bl1z-1+bl2z-2+…blnz-n,blj∈R1,l=2,…,p-1,j=1,2,…,n.


(9)
其中
ςi(kT)=[-yi(kT-T), -yi(kT-2T), …,-yi(kT-nT),
ui(kT),ui(kT-T),ui(kT-nT),ui(kT-T+t1),
ui(kT-2T+t1), …,ui(kT-nT+t1), …,
ui(kT-T+tp-1),ui(kT-2T+tp-1), …,
ui(kT-nT+tp-1)]T
fh[ςi(kT)]是第h个非线性加权函数;gh[ςi(kT)]是在第h个工作点处的局部线性模型。
最后,得到了描述系统(3)的多模型一般表达形式
yi(kT)=fi[ςi(kT)],i=1,2,…,q
(10)
注1:由于每个智能体的fi(·)的函数结构是不同的,因此q个智能体组成的多智能体系统是异构的。

3 分布式无模型自适应控制
对于模型(10),各个智能体可视作多输入单输出(MISO)的非线性系统.其中,第i个智能体的动态模型如下:
yi(kT+T)=fi[ςi(kT+T)]
=fi(yi(kT),…,yi(kT-nyT),ui(kT),…,
ui(kT-nuT)),ny=nu=n-1,i=1,2,…,q
(11)
其中,
分别表示智能体i在kT,…,kT-nuT时刻的输入数据,ui∈Rp;ny和nu是未知的正整数;fi(…)是非线性函数。
假设1[25]:fi(…)关于第(nu+ny+2)个变量具有连续的偏导数。



(12)
其中

证明:由式(12)知
Δyi(kT+T)
=fi(yi(kT),…,yi(kT-nyT),ui(kT),…,ui(kT-nuT))-fi(yi(kT),…,yi(kT-nyT),ui(kT-T),
ui(kT-T),…,ui(kT-nuT))+fi(yi(kT),…,yi(kT-nyT),ui(kT-T),ui(kT-T),…,ui(kT-nuT))-fi(yi(kT-T),…,yi(kT-nyT-T),
ui(kT-T),…,ui(kT-nuT-T)),i=1,2,…,q
(13)
令
ψi(kT)=fi(yi(kT),…,yi(kT-nyT),ui(kT-T),
ui(kT-T),…,ui(kT-nuT))-fi(yi(kT-T),…,yi(kT-nyT-T),ui(kT-T),…,ui(kT-nuT-T)),
i=1,2,…,q
根据假设1和微分中值定理,式(13)可整理成如下形式

(14)
固定采样时刻k,考虑含变量Ηi(kT)∈R1×p的方程为
ψi(kT)=Ηi(kT)Δui(kT),i=1,2,…,q
(15)


根据一致性理论,考虑通信拓扑结构固定,对多智能体系统(11)设计如下控制协议(16)~ (19)。
i=1,2,…,q
(16)
sign(il(kT))≠sign(il(T)),l=1,2,…,p
(17)
为使各个智能体的输出都跟踪上期望轨迹,本文设计如下的控制律

(18)
Θi(kT)=ci[y*(kT+T)-yi(kT)]

(19)
其中,y*(kT+T)是参考信号;若ci=1表示智能体i可以接收虚拟领导者的参考信号,否则ci=0;aij表示网络拓扑中权值邻接矩阵A=[aij]n×n中元素;λ>0是权重因子,用于控制智能体i的输入量的变化.ρ是步长因子。
现在的任务是,控制器的步长因子ρ的取值满足什么条件时,多智能体系统能够实现的一致的跟踪效果。
4 一致性分析
为便于收敛性分析,下面给出如下假设和引理。
引理 1:对于非均匀采样非线性多智能体系统(11),在满足假设1和假设2的条件下,如果η∈(0,1),μ>0,则各个智能体线性化参数估计算法(16)给出的伪偏导数估计值i(kT)是有界的。


Φi(kT-T)-Φi(kT)
(20)
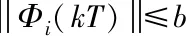
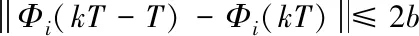
(21)
结合(21)式,将式(20)两边同时取范数,

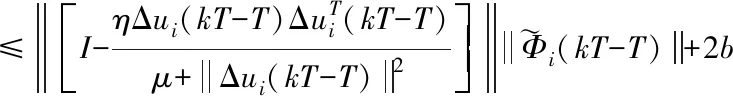
(22)
对(22)式不等式右边第一项取平方有
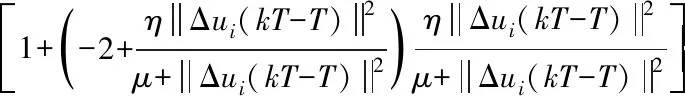


(23)
因此存在常数d,满足

(24)
根据式(22)和式(24),可得到如下的递推不等式
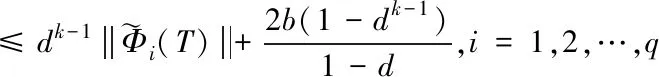
(25)
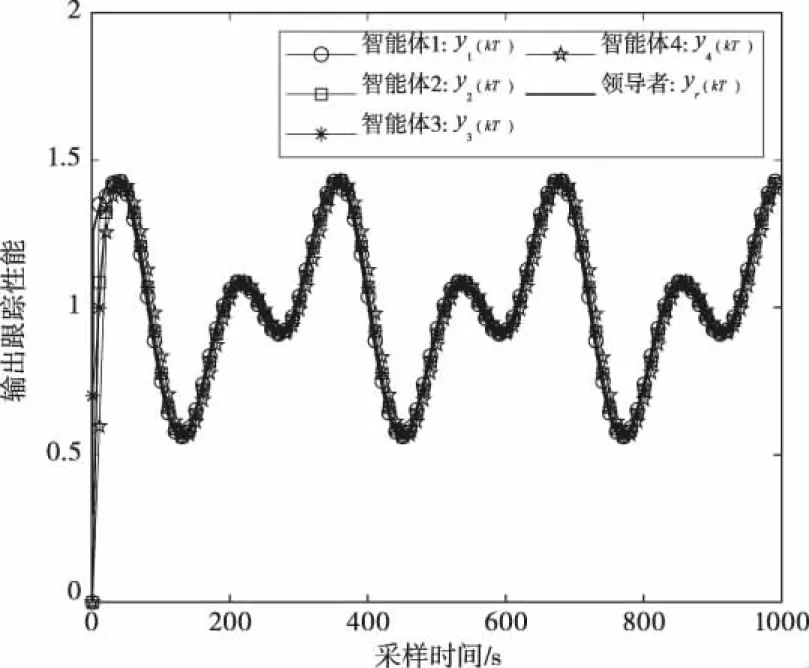
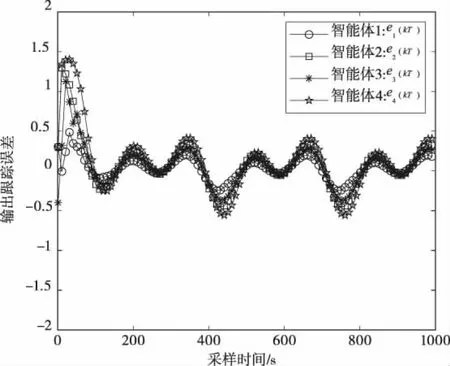
0 (26) 证明:令 0 引理3[26]:令W(t)是一个时变的主对角线元素为正的不可约的次随机矩阵.其中,W⊂RN×N表示所有可能的W(k)组成的集合。使得 其中,0<ϖ<1,且W(t),t=1,2,…,L。L个矩阵是从集合W中任意选取。 假设3:拓扑图G是强连通的,且者少有一个智能体可以获取领导者的参考轨迹信息。 注2:假设3中的通信条件是多智能体系统一致性控制问题可解性的必要条件。如果存在一个孤立的智能体,它甚至不知道控制目标,那么该智能体就不可能遵循领导者的参考轨迹。 根据上述分析,下面给出以下的结论: 定理 2:非均匀采样非线性异构多智能体系统(11),在假设1、2和3满足的条件下。若虚拟领导者的期望轨迹输出为y*(kT+T)=y*=const,采用式(16)~式(19)的控制协议,且控制器的参数满足,μ>0,η∈(0,1),λ>λmin。当下面的条件成立时 则所有智能体的输出在k→∞时,存在 证明: 定义跟踪误差ei(kT) ei(kT)=y*(kT+T)-yi(kT) (27) 式(19)重新整理为 i=1,…,q (28) 为便于收敛性分析,需定义如下的堆栈向量: (29) 因此,考虑网络中的q个智能体,结合式(12)和式(28),则式(27)可改写成以下紧凑形式 E(kT+T)=[I-Φ(kT)P(kT)[L+C]]E(kT) (30) 其中,L[lij]∈RN×N是拉普拉斯矩阵,表示智能体i与虚拟领导者之间的联系,若ci=1表示智能体i有权获取虚拟领导者的期望轨迹y*,否则ci=0。 令Ψ(kT)=I-M(kT)[L+C],其中 M(kT)=Φ(kT)P(kT)=ρ×diag[mi(kT)] (31) 因此,式(30)可重新整理为 E(kT+T)=Ψ(kT)E(kT) (32) 因为不同智能体间的网络拓扑图是强联通的,则矩阵Ψ(kT)一定是不可约矩阵.当ρ满足下面的条件时, (33) 由引理2知0 下面对式(32)进行递推运算,并对不等式两边同时取范数得 (34) 由引理1可知,不等式(34)可重新整理为, (35) 又因为0<ϖ<1,k>L,则 (36) 定理 3.对于网络通信拓扑是强联通结构的非均匀采样非线性异构多智能体系统(11),在假设1、2和3满足的条件下,若虚拟领导者的期望轨迹输出为有界的时变信号y*(kT+T),采用式(16)~式(19)的控制协议,且控制器的参数满足,μ>0,η∈(0,1),λ>λmin。当下面的条件成立时 各个智能体的输出在k→∞时,跟踪误差有界。 证明: 定义跟踪误差ei(kT)以及时变参考信号在采样周期T内的变化Δy*(kT+T)如下 ei(kT)=y*(kT)-yi(kT) (37) Δy*(kT+T)=y*(kT+T)-y*(kT) (38) 根据式((37)和式(38)将式(19)重新整理为 Θi(kT)=ci[y*(kT+T)-yi(kT)]+ ciΔy*(kT+T) (39) 因此q个智能体的控制协议可改写成以下紧凑形式, ΔU(kT)=P(kT)[L+C]E(kT)+P(kT)CΔR(kT+T) (40) 其中,ΔR(kT+T)=Δy*(kT+T)⊗1q。 下面考虑跟踪误差的紧凑形式 E(kT+T)=E(kT)-Φ(kT)ΔU(kT)+ΔR(kT+T) (41) 将式(40)带入到式(41)中得 E(kT+T)=[I-Φ(kT)P(kT)[L+C]]E(kT) -Φ(kT)P(kT)CΔR(kT+T)+ΔR(kT+T) (42) 令Ψ(kT)=I-Φ(kT)P(kT)[L+C]=I-M(kT)[L+C]∈Rq×q S(kT)=Φ(kT)P(kT)C∈Rq×q 则式(42)重新整理为 E(kT+T)=Ψ(kT)Ψ(kT-T)Ψ(kT-2T)…Ψ(kT-LT) ·Ψ(kT-LT-T)Ψ(kT-LT-2T)…Ψ(kT-2LT)… Ψ(kT-nLT-T)Ψ(kT-nLT-2T)…Ψ(kT-(n+1)LT) …Ψ(3T)Ψ(2T)Ψ(T)E(T)+Ψ(kT)Ψ(kT-T)… Ψ(2T)ΔR(2T)+Ψ(kT)Ψ(kT-T)…Ψ(3T)ΔR(3T)+ …+Ψ(kT)Ψ(kT-T)ΔR(kT-T)+Ψ(kT)ΔR(kT)+ΔR(kT+T)+Ψ(kT)Ψ(kT-T)…Ψ(2T)S(T)ΔR(2T) +Ψ(kT)Ψ(kT-T)…Ψ(3T)S(2T)ΔR(3T)+… +Ψ(kT)Ψ(kT-T)S(kT-2T)ΔR(kT-T)+Ψ(kT)S(kT-T)ΔR(kT)+S(kT)ΔR(kT+T) (43) 当步长因子ρ满足 由引理2可知0 对式(43)两边同时取范数得 (44) 因为 S(kT)=Φ(kT)P(kT)C(kT)∈Rq×q 因此式(44)可重新整理为 (45) 根据向下取整函数⎣·」的特点,下面令 r×[d2+1](λ(k)+λ(k-1)+…+λ(1)+λ(0)) (46) 因此 (47) 综上所述,由式(45),(46)和(47)可知,当k→∞时, (48) 因此,跟踪误差是有界的,证明完毕。 考虑4个智能体按图2所示的网络拓扑结构连接,每个智能体的模型为 图2 网络拓扑结构 +1.4u1(kT+t1-T)+0.7sin(0.5(y1(kT)-y1(kT-T))) Agent2:y2(kT+T)=u2(kT)+1.1u2(kT+t1-T)× +1.4u3(kT+t1-T)+0.7cos(0.5(y3(kT)-y3(kT-T))) (49) 其中,各个智能体的非均匀采样方案为,T=1s,p=2,t1=0.4s。通过对非线性系统的分析,每个智能体都是异构的、非最小相位系统。值得说明的是本文讨论的是动态特性未知的异构多智能体系统,在控制协议的设计中不包含任何模型参数信息,上述模型只是用来产生相应的输入和输出数据。 图2中的节点0表示虚拟领导者,作用是为网络中的部分智能体提供期望的参考信号。该网络拓扑只有智能体1和智能体3可以直接获得虚拟领导者的参考信号,而智能体2和智能体4只能通过与邻居智能体的数据交换来实现跟踪。 (50) 显然,拓扑图G是强连通结构,且 下面给出恒定的参考信号形式如下 (51) 由图3~图4可知,虽然多智能体系统中,有部分智能体无权获得虚拟领导者的参考信号,但是所有智能体都能随着采样时间的增加实现输出跟踪的一致性。即使参考信号在500s发生变化,系统也能在520s左右继续跟踪上参考信号,且跟踪误差最终收敛于0,这验证了定理2有效性。从图5看出,系统伪偏导数估计值φi1(kT)和φi2(kT),i=1,2,3,4是慢时变的有界函数,显然满足引理1。 图3 输出跟踪性能 图4 输出跟踪误差 图5 系统的伪偏导数变化 下面给出时变的参考信号形式如下, (52) 由图6~图8看出,网络中的所有智能体均跟踪上虚拟领导者的期望轨迹,且不同智能体的跟踪误差是有界的,验证了定理3的有效性。同时,系统伪偏导数估计值φi1(kT)和φi2(kT),i=1,2,3,4是变化较为平稳的慢时变有界函数,其动力学行为与各个智能体的闭环系统工作点、控制信号有关。 图6 输出跟踪性能 图8 输出跟踪误差 此外,为验证所提方法的性能,采用固定增益的一致性控制方法跟踪参考信号(52)。考虑P型分布式控制算法[19],ui(kT)=ui(kT-T)+KiΘi(kT),i=1,2,…,p。在仿真过程中使用相同的初始条件,对于所有的智能体选择Ki=[0.01 0.01]T。图9给出了输出跟踪误差的仿真结果。从图8和图9的比较中,可以明显的看出本文方法的跟踪误差较小。 图9 输出跟踪误差 针对非均匀采样非线性多智能体系统的一致性控制问题,提出一种基于数据驱动的分布式控制策略。首先,采用多模型方法表示非均匀采样非线性系统,推导出每个智能体在当前工作点处等价的紧格式动态线性化(CFDL)数据模型。然后,利用系统的输入和输出数据估计伪雅可比矩阵(PJM)的参数,并利用一致性理论对各个智能体设计出相应的分布式无模型自适应控制器,该控制器仅依靠非均匀刷新的输入信号和周期采样的输出信号以及邻居智能体的输出数据,无需被控对象的准确模型信息。同时该方法克服了传统的神经网络控制需要大量的训练数据的缺点,计算效率更高,更便于工程实现。 在未来的工作中,将进一步深入研究切换拓扑结构下的非均匀采样非线性多智能体系统的一致性控制问题,以及在事件触发机制下的分布式无模型控制方法。因此,这方面的后续研究非常有意义。














5 数值分析









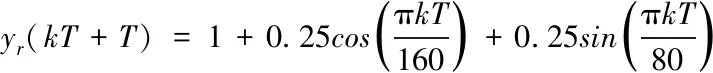

6 结论

