基于快速SBL的ISAR稀疏孔径机动目标成像方法
朱瀚神,胡文华,郭宝锋,朱常安
(陆军工程大学石家庄校区,河北石家庄 050003)
1 引言
逆合成孔径雷达具有全天时、全天候、作用距离远和分辨率高等特点,能够获得目标的二维图像,有利于目标分类与识别,在民用和军用领域应用广泛[1]。当ISAR对非合作目标进行成像时,补偿形成的转台模型往往具有复杂的机动分量,其方位向多普勒频率具有时变性,导致传统RD算法对其成像时发生散焦。
为了对机动目标清晰的成像,国内外进行了深入研究,其方法主要包括两种:1、基于时频分析的瞬时距离多普勒(Range-Instantaneous-Doppler,RID)成像方法,通过时频分析技术对补偿后的一维距离像对每个距离单元进行时频变换,选择最优时刻的瞬时频谱作为目标瞬时ISAR像[2]。但这类方法通常需要对每一个距离单元进行分析,计算代价大,实时性能差。2、基于参数化建模的成像方法,参数化建模的方法旨在处理同一距离单元中的回波信号时,建立对应的数学模型,根据算法估计模型参数,重构方位向信号,获得相应的ISAR图像。根据机动目标的运动形式,通常把回波建立为线性调频信号(Linear Frequency Modulation,LFM)模型或立方相位信号(Cubic Phase Signal,CPS)模型[3]。但参数估计需要针对每个散射点建立数学模型,在复杂电磁背景下,散射点的个数难以确定,参数估计得准确性难以得到保证,补偿时理论上也只能补偿同一距离单元内等效散射点的相位偏差。
雷达宽窄带信号交替发射难以长时间连续观测目标、提升抗干扰性能使用的频率捷变技术、非合作目标姿态的不确定性导致难以测量等情况都会引起雷达方位向回波的缺失,这种信号不连续的情况被称为稀疏孔径[4]。压缩感知(Compressed sensing,CS)[5]理论提出在满足欠采样的条件下,可以通过少量测量精确恢复稀疏信号与雷达中稀疏孔径采样模式相契合,因此CS理论因其采样率低,成像清晰等优点广泛的应用于ISAR成像中。但是在稀疏ISAR成像中,现有的大多数成像方法大多基于两个假设:1、目标在相干处理间隔(Coherent Processing Interval,CPI)内均匀旋转。2、没有产生跨距离单元距离徙动(Migration Through Resolution Cell,MTRC)[6]。机动目标因其转动的非均匀性,散射点运动会跨距离门产生徙动,所以这些假设对于是无效的。目前通过CS理论对ISAR稀疏孔径机动目标重构恢复成像的方法主要分为基于l1范数的凸优化类算法;贪婪迭代类方法,如正交匹配追踪法(Orthogonal Matching Pursuit,OMP),这种方法成像速度快,但成像精度较低;基于统计理论将稀疏信号重构问题转化为统计问题的贝叶斯学习法(Sparse Bayesian Learning,SBL),如文献[7]提出的多响应稀疏贝叶斯学习(Multi-response Sparse Bayesian Learning,MSBL)方法,但是MSBL涉及到大量的矩阵求逆运算,计算量较大,且该算法抗噪性能较差。本文提出了一种基于快速稀疏贝叶斯学习的ISAR稀疏孔径机动目标成像算法。首先对平动补偿后的回波稀疏化处理,根据机动目标回波特性建立含参数γ的稀疏基矩阵,然后在实数域通过多维矢量分组处理的方式利用SBL的快速边缘似然函数最大化算法进行图像重构,最后合成得到二维目标图像。仿真验证了算法的有效性和优越性。
2 ISAR稀疏孔径机动目标成像模型
2.1 ISAR机动目标回波模型
本文以匀加速旋转目标为例,假设平动补偿已经完成,目标运动可等效为转台模型,如图1所示。

图1 机动目标转台模型
远场条件下,以目标旋转中心O点建立笛卡尔直角坐标系,X轴为方位轴,Y轴为雷达视线轴。在相干处理时间内,瞬时雷达视角为θ(t),0≤t≤T0,其中T0为观测时间,目标上一点P(xn,yn)距雷达的瞬时距离为
R(t)=r(tm)+xnsinΔθ(t)+yncosΔθ(t)
(1)
Δθ(t)为成像时间内的旋转角度,小角度情况下可近似认为sinΔθ(t)≈Δθ(t),cos Δθ(t)≈1,而在目标机动情况下,Δθ(t)由泰勒级数展开为

(2)
式中,t0表示成像初始时刻,ω为目标的角速度,ω′为目标的角加速度。雷达通常发射LFM信号

(3)

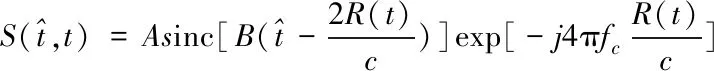
(4)
式中,c为光速,B=Tpμ为发射信号带宽,假设距离单元内包含K个散射点,将式(1)带入式(4)中,可得到信号为

(5)
由上式可以看出,当目标机动飞行时,散射点的多普勒频率会产生时变。正是这个性质导致传统的RD算法成像发生散焦,此时的多普勒频率为

(6)
2.2 含参数γ的匹配稀疏基建立

矩阵FR=[FR(1),FR(2)…FR(q)…FR(Q-1)]代表距离向含参数傅里叶变换字典。每一个元素为,FR(q)=exp[-j2π(1+γtn/2)tnfdq],其中,fd=[-Q/2:Q/2-1]*Δfdq,Δfd=1/M*PRT为多普勒分辨率,Q=fr/Δfd为多普勒单元数。矩阵FA=[FA(1),FA(2)…FA(m)…FA(M-1)]代表方位向含参数傅里叶变换字典,每一个元素为FA(m)=exp[-j2π(1+γtn/2)tnfdq],其中tm=[1:M]TΔtm为方位向慢时间序列,Δtm=1/fr,N为脉冲数。由此建立出含二次项的稀疏基矩阵F,该矩阵相比于通常使用的傅里叶矩阵更加符合ISAR机动目标回波特征,仿真验证了它的优越性。
2.3 稀疏孔径成像模型
式(5)为方位全孔径信号表达式,前文所提到的实际中的各种问题都会引起雷达方位向回波的缺失,这种缺失分为数据随机缺失和数据块缺失两种情况。假设S为有效孔径全部回波,其中含有K(K SK×N=TK×LSL×N=TFALLA+ε=FA+ε (7) 式中,TK×L为数据选择矩阵,可以消除SL×N中缺失孔径,合并有效孔径。FALL为稀疏基字典,A为所求高分辨图像,ε为K×N的复噪声矩阵。 目前的稀疏恢复算法主要包括基于lp范数正则化、贪婪追踪和稀疏贝叶斯学习三类方法。其中,最常见的lp范数正则化类恢复算法包括l0范数的非凸优化算法和l1范数的凸优化算法,这类算法运算时间长,恢复精度不高。贪婪追踪算法运算效率较高,但同样面临重构精度不高的问题。而稀疏贝叶斯重构方法不仅考虑了信号的稀疏特性,而且引入了稀疏目标的先验统计信息即测量过程中的加性噪声因而能够更好的进行参数求解,重构精度较高[10]。 为了减少计算量,采用文献[6]的拆分思想,将二维回波矩阵SK×N按距离单元分成若干块后逐块进行处理。假设每块数据矩阵中包含N1个距离单元的回波数据,则N个距离单元的回波数据一共可分为H=「N/N1⎤块(「⎤表示向上取整),在求解时先逐块数据进行重构,再合成二维图像。对于其中每一块数据块都首先进行回波矩阵是矢量化,把数据写成稀疏贝叶斯回归模型形式,即 (8) 另一方面,进行ISAR成像时的回波信号通常为复数信号,而SBL算法的求解一般基于实数求解,所以需要通过变换矩阵把复信号转化至实数表示,其转化形式如下 (9) 式中,Re()和Im()分别表示实部和虚部。转化之后再利用快速SBL算法求得包含实部和虚部信息的目标矢量a1[11]。 设噪声ε的虚、实部分别服从方差为σ2的实高斯分布,假设观测数据sm之间相互独立,则观测数据集的似然函数可表示为 (10) 对a1赋予零均值的高斯先验分布 (11) 其中,ai表示a中的第i个元素,这一种先验分布被称为自动相关(Automatic relevance)先验分布。该先验分布中矢量α有N+1个超参数矢量。为完成分层先验概率的描述,对α和模型中的剩余参数(如σ2)定义超先验概率,这些参数量可用尺度参数来进行描述,并适合用Gamma先验分布来进行描述,即 (12) P(β)=Gamma(β|c,d) (13) 图2 稀疏系数多层概率图模型 (14) (15) (16) 此时对于超参数α的估计可以通过type-II模型得到,也就是说,稀疏贝叶斯“学习”被公式化为相对于边际似然度α的(局部)最大化,或者等价地,其对数L(α): (17) 为使代价函数最大化,将矩阵C进行分解,可得到 (18) 展开代价函数,可得 =L(α-i)+L(αi) (19) 式中,α-i表示从α中除去第i个超参数αi后剩下的超参数集合,为了简化后文的表达式,定义 (20) (21) 由文献[14]可知L(α)相对于αi具有唯一的最大值 (24) (25) 式中,B=σ-2I,则 (26) (27) 图3 算法流程图解 图4 散射点模型图5全孔径RD成像结果 如图所示,基于快速SBL算法的ISAR稀疏孔径机动目标成像过程可描述如下:在转台模型的回波基础上,构造含参数γ的匹配稀疏基矩阵,然后利用数据选择矩阵T消除缺失孔径、合并有效孔径,得到稀疏孔径二维回波SK×N,并按距离单元进行分块处理,将每块回波矢量化并转入实数域,通过快速SBL算法得到目标图像估计值μ后进行合成形成稀疏孔径机动目标二维图像估计值。 通过仿真验证本文方法对于机动目标的成像能力。雷达参数设置如下:雷达载频为10GHz,脉冲宽度为20μs,带宽为800MHz,脉冲重复频率为50Hz,观测时间内发射500个脉冲;目标做匀加速旋转,其中转动角速度为0.005rad/s,转动角加速度为0.0005rad/s,下图为目标的等效散射点模型。为了便于说明,首先使用RD算法对全孔径回波进行成像。 为了能够得到清晰完整的ISAR机动目标图像,根据回波特征建立了相匹配的稀疏基字典。为了说明所建立匹配稀疏基的优越性,在使用本文算法,SNR为5dB,稀疏孔径为50%随机稀疏的条件下,分别使用Fourier稀疏基和匹配稀疏基进行仿真,得到成像结果如图5所示。 图5 使用Fourier基(左)与匹配稀疏基(右)成像结果 图6 SNR5dB 50%随机稀疏成像结果 图7 SNR5dB 75%随机稀疏成像结果 图8 SNR5dB 50%块稀疏成像结果 图9 SNR5dB75%块稀疏成像结果 图10 不同信噪比算法成像结果 由结果可知,由于目标的非均匀转动,在Fourier稀疏基下的CS成像出现了大量的虚假散射点,能量聚焦效果差,散焦严重。而基于本文方法的机动目标成像效果较好,散射点聚焦清晰,能量汇聚集中,成像质量高,验证了所建立与回波相匹配的稀疏基字典对提升成像质量的有效性。 为了验证算法的成像性能,通过典型的RD算法、OMP算法、MSBL算法和本文算法同时对ISAR机动目标稀疏孔径回波进行成像。 首先,为了验证不同算法在不同孔径缺失下的成像性能,统一设置SNR为5dB,通过改变孔径缺失情况,使用上述四种算法进行成像。从上至下为50%数据随机缺失、75%数据随机缺失、50%数据块缺失、75%数据块缺失的情况,从左至右依次是RD算法、OMP算法、MSBL算法和本文算法的成像结果。 从成像结果可以看出,使用RD算法对ISAR机动目标成像会因其多普勒的时变而产生散焦现象,而在稀疏孔径情况下继续使用RD算法成像会产生大量的能量泄露,并加重散焦的程度。为更好说明算法性能,采用TBR、图像对比度C和熵作为说明成像质量的指标,并记录下成像所用时间,列表如下。其中,TBR能有效表征目标图像的能量聚焦程度,可以评价目标图像的噪声抑制能力和聚焦能力,值越大越好;图像对比度可以评价目标图像的整体聚焦质量,也是值越大越好;熵反映了图像中平均信息量的多少,图像信息熵越小说明其散焦抑制较好,虚假散射点较少,成像质量越好。 表1 成像方法性能对比 表2 成像时间对比 表3 不同信噪比算法成像指标对比 由上表可以看出,在使用含参数γ的匹配稀疏基矩阵情况下采用OMP算法和MSBL算法成像可以提高成像质量,散焦现象得以抑制。但是,孔径缺失较多时,OMP算法不能清晰的分辨出原散射点,发生模糊并产生虚假散射点,MSBL抗噪性能较差,受噪声影响较大,成像质量迅速下降。采用本文算法进行成像时,不仅抑制了散焦现象,能够清晰分辨出各个散射点,在孔径缺失数量较多时,也仍然能够清晰的重构出目标图像。在使用SBL算法求解时,本文算法相比于MSBL算法所用时间更少,运行速度更快,体现了本文算法时间上的优越性。 另一方面,为了验证算法在不同SNR条件下成像效果,以OMP算法作为对比算法,验证在不同SNR条件下,上述指标的变化情况。统一设置为50%随机缺失稀疏孔径,同时上图为SNR为5dB成像结果,下图为SNR为10dB结果,左侧为OMP算法结果,右侧为快速SBL算法成像结果。 从表中数据可以看出,在同一SNR条件下,本文算法成像结果相较于OMP算法TBR值和C值都有提高,说明同一SNR条件下,本文算法成像结果相对于OMP算法来说能力聚焦能力强、噪声抑制能力好。另一方面,随着SNR减小,两种算法所得图像的TBR值和C值均减小,但本文算法的指标均好于OMP算法,说明在低SNR条件下,利用快速SBL的ISAR稀疏孔径机动目标成像算法能够得到比OMP算法得到更高质量的图像,实现更高精度的重构,体现了本文算法的优越性。 本文根据机动目标回波特征建立含参数γ的匹配稀疏基矩阵,提出一种通过快速边缘似然函数最大化的方式求解SBL问题的快速SBL的ISAR稀疏孔径机动目标的成像方法。在机动目标多普勒频率时变情况下,得到了较为清晰的ISAR图像。仿真结果表明,本文算法相比于经典的OMP算法和MSBL算法成像质量更高,运算效率更高,孔径缺失数据较多情况下重构效果更好,抗噪性能更优。3 快速稀疏贝叶斯学习算法

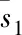

3.1 稀疏先验模型





3.2 快速边缘似然函数最大化求解


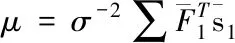


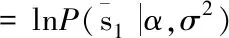










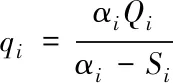



4 仿真与分析
4.1 基于匹配稀疏基的SBL算法成像


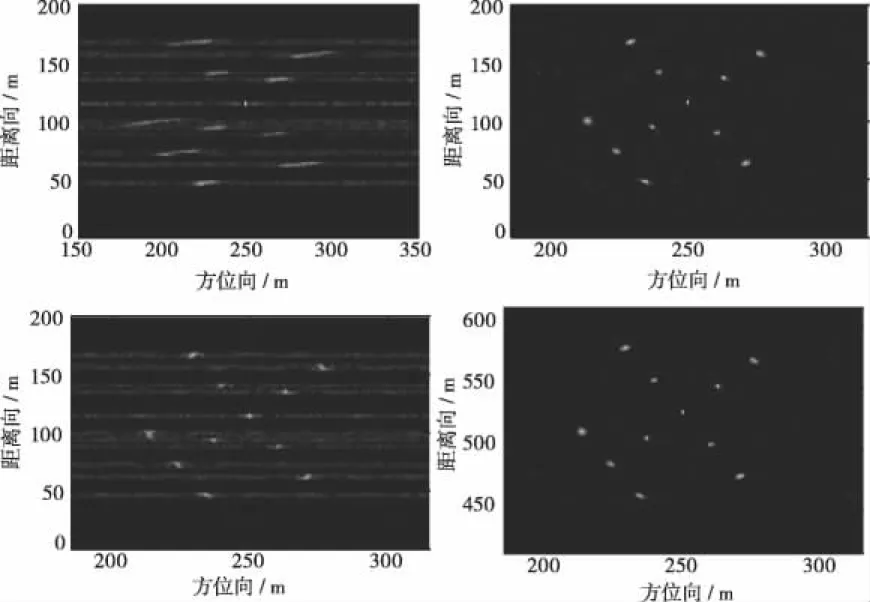


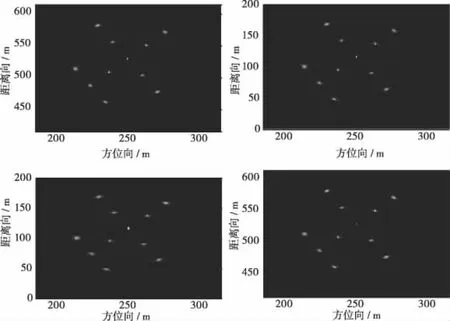
4.2 ISAR机动目标稀疏孔径成像仿真
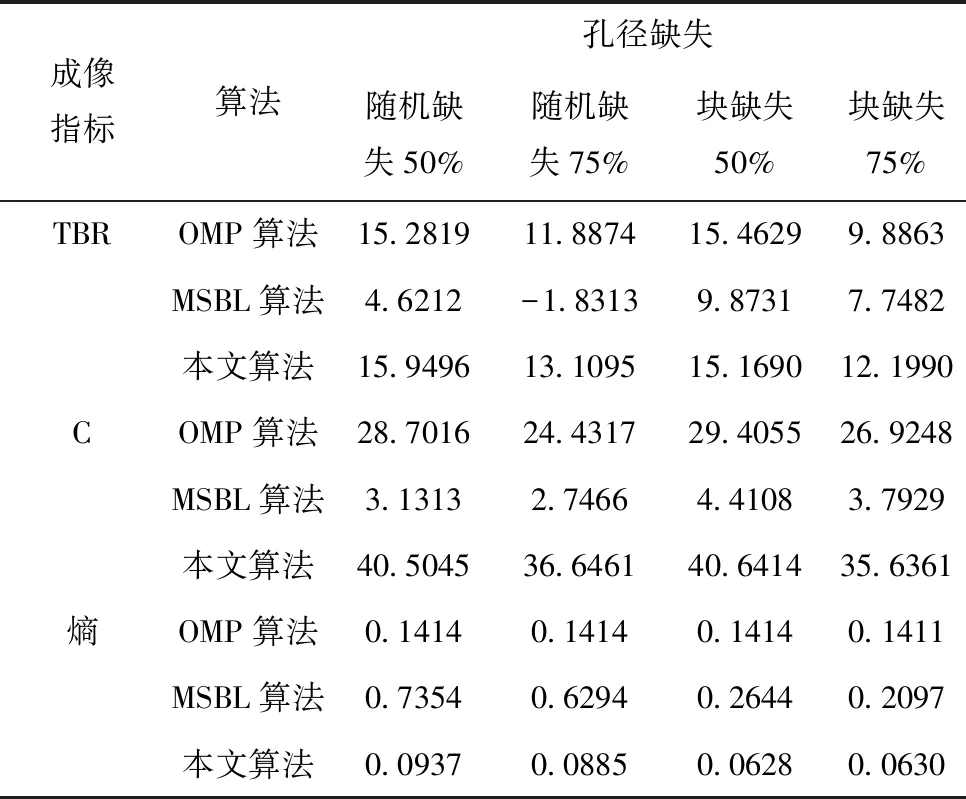


4.3 算法抗噪性能验证
5 结束语

