基于SA的光伏出力概率密度预测方法

邢 晨,温 蜜,张照贝

(上海电力大学计算机科学与技术学院,上海,201303)

1 引言

为加快能源转型,构建清洁能源电网,大规模发展风力、光伏、潮汐等新能源势在必行[1]。新能源是基于新时代背景下衍生的全新能源,其具有储备丰富、可再生且低污染的优点,这也是未来经济社会发展的主要趋势。光伏发电作为较为成熟的可再生能源发电技术之一,近几年发展得十分迅速[2]。然而光伏发电受天气条件影响显著,光伏发电存在间歇性工作的特点,这给制订发电计划和电网调度带来了巨大挑战。因此,如何建立准确的光伏出力预测模型,对电力系统运营商制定发电计划和调度具有重要意义。

目前预测方法根据预测结果的不同可分为确定性预测和概率预测两类。确定性预测方法主要包括长短期记忆网络(LSTM)[3,4]和时间卷积网络(TCN)[5,6]等深度学习模型。文献[7]提出一种基于卷积神经网络(CNN)的光伏出力预测模型,证实CNN具有良好的特征提取能力。文献[8]建立以门控循环神经网络(GRU)为基础的预测模型,验证了GRU相对于LSTM等在结构上更为高效和简单的优势。文献[9,10]采用Seq2seq网络结构进行预测,提高了模型的学习效率和预测水平,深度学习模型具有强大的学习能力和较高的预测精度。但是,确定性预测的预测结果为一个期望值,无法计及未来功率的波动范围,在涉及不确定性问题难以满足实际需求[11]。

概率预测可以更加全面的反映光伏出力相关信息,现如今已成为预测的主要方法[11-16]。文献[14]提出一种结合CNN和QRGRU的概率密度预测方法,可以很好的解决概率密度预测问题;文献[15]提出了一种基于QRLSTM的概率预测模型,验证了概率预测模型相对于传统模型预测的优越性;文献[16]提出了一种基于藤copula分位数回归的光伏功率预测模型;以上文献都证实了分位数回归在概率预测中的优越性,但以上方法大多是对模型的融合,未对影响光伏出力的特征进行分析和挖掘。

由以上分析可知,确定性预测方法不能反映光伏出力的不确定性,而近年来的不确定性预测方法虽然可以提供不确定性分析,但在特征挖掘方面存在不足,从而在预测精度方面往往难以满足要求。为此,提出一种基于Seq2seq-Attention的方法对光伏出力进行概率预测。首先,采用四分位法和三次样条插值法对数据进行预处理,增强数据的可用性;然后,分别采用K-shape, FCM和层次聚类三种聚类方法对数据进行分簇,构建新的输入特征,提高特征的有效性;最后,构造QR-Seq2seq-Attention模型预测光伏出力,再利用核密度估计得到未来时刻出力的概率密度曲线,反映光伏出力的不确定性。通过澳大利亚光伏电站数据集验证提出方法预测性能。

2 算法理论介绍

2.1 异常值检测和填充

2.1.1 四分位法

四分位法可以进行异常值检测。若一个数据点位于[QL,QU]之外,则这个数据即可被认为是异常值。其原理图如图1所示。

图1 四分位法原理

[QL,QU]=[q1-1.5*QR,q3+1.5*QR]

(1)

在计算公式中,下四分位数q1和上四分位数q3分别是第一和第三分位数。QR为四分位数区间,即QR=q3-q1,下限是QL,上限是QU。

2.1.2 三次样条插值

通过四分位法检测到的异常值可以通过样条插值进行修正。样条插值不仅获得了更高的多项式插值次数,且由于龙格现象也保持了稳定性。因此,本文中采用三次样条插值的方法进行异常值替换。

假设有N+1个数据样本,{(xi,yi),i=0,1,…,N},且x0≤x1≤…≤xN。构造了一个满足S(xi)=yi的样条函数S(x)。样条曲线是区间x∈[xi,xi+1]的三次多项式函数。

S(x)=ai+bix+cix2+dix3

(2)

其中ai,bi,ci,di为三次多项式系数,用于保证数据平滑性。且函数S(x)必须保证S(x),S′(x),S″(x)在任何地方都是连续的。

综上,通过上述异常值检测方法和插值对异常值进行修正获得连续平滑的曲线,这条曲线上的点有助于建立准确的光伏出力预测模型。

2.2 门控循环神经网络 (GRU)

GRU模型于2014年[17]提出,其内部结构类似于LSTM模型,如图2所示,其主要对LSTM的计算过程进行简化,没有明显降低计算精度。GRU模型将LSTM的两个状态变量合并为一个隐藏状态变量h,重新划分了门的结构,将LSTM中的输入门,遗忘门和输出门替换为重置门和更新门。以上改变使得计算参数减少,其计算过程如下所示。

图2 GRU模型原理

zt=σ(WZ[xt,ht-1]+bz)

(3)

rt=σ(Wr[xt,ht-1]+br)

(4)

(5)

(6)

近年来,通过实例[18]表明GRU作为LSTM的衍生模型,计算速度得到提升,计算复杂度降低,因此GRU模型在各个领域得到广泛应用。

2.3 聚类算法

2.3.1 K-shape

K-shape与传统的K-means聚类相似,计算过程包括一个迭代过程和一个细化过程。K-shape的原理是应用互相关信息找出集群的质心,然后对每个簇的成员进行不断的迭代更新。K-shape的距离度量不受时间尺度缩放和位移的影响[19],由于其存在位移不变性的优点,因此选择互相关最大的位置确定聚类的质心。K-shape对时间序列形状相似度计算如下

(7)

其中Cω(X,Y)为不同出力序列的互相关信息,R0为两出力序列没有相对位移时对应的互相关信息。

在细化的过程中,每个集群中更新的成员也会导致质心的变化,此算法的目标是使新的质心与其它时间序列数据的相似性最大化。

2.3.2 模糊C均值聚类(FCM)

FCM是K-shape的一种改进算法。其基于目标函数实现聚类。其基本思想是将被划分到同一簇的成员之间的相似度最大。令出力序列为X={x1,…,xn},A={a1,…,ac}为聚类中心的集合。FCM的目标函数公式如下

(8)

2.3.3 层次聚类

层次聚类是一种用于数据的分析的流行聚类技术之一[21]。分层聚类的优点在于其灵活且对底层数据的假设较少。层次聚类的过程中,最开始,所有的数据点都被视为一个单独的聚类。首先,它对两个彼此靠近的集群进行识别,然后合并这些集群成为一个大集群,不断重复这个过程,直至将整个数据集都包含到单个集群中,根据正在合并的两个集群之间的距离的变化,可以确定最后的聚类数量。

3 提出的Seq2seq-Attention的光伏出力概率密度预测方法

提出的光伏出力概率预测方法流程图如图3所示。预测过程分为四个阶段:数据预处理,特征重构、构造QR-Seq2seq-Attention预测模型及核密度估计。

图3 提出方法流程图

其详细步骤如下所示:

第一步,将输入的原始数据集进行归一化处理,采用四分位法和三次样条法进行异常值检测和异常值填充;

第二步,采用K-shape、FCM和层次聚类三种方法将特征集分为四类,将类别作为新的特征构建新的数据集;

第三步,将数据集划分为训练集和测试集,采用Seq2seq-Attention模型及基准模型对训练集分别进行分位数回归预测;

最后,通过核密度估计得到概率密度预测结果,绘制相关概率密度曲线。

3.1 数据预处理

由于数据存在不同的量级,因此需要对数据进行归一化处理,其计算公式为

(9)

式中x为原始数据值,xmax和xmin分别为原始数据的最大值和最小值。xn为经过归一化处理后的数据。

采集的光伏出力数据通常包含着客观的误差,这些误差可能是由传感器故障引起。以往的研究通常直接基于采集的数据,缺乏准确性。为了增加数据的可用性,首先采用四分位法进行异常数据检测;再采用三次样条插值法进行异常值填充,流程如图4所示。

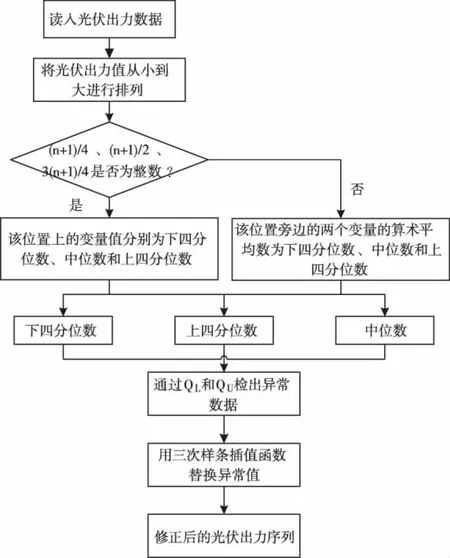
图4 数据预处理流程

其详细步骤如下:

Step1:将光伏出力值从大到小进行排列;

Step2:分别判断(n+1)/4、(n+1)/2、3(n+1)/4是否为整数,从而确定相应的下四分位数、中位数和上四分位数;

Step3:检出在上界和下界范围之外的异常值;

Step4:采用三次样条函数替换异常值得到修正后的光伏出力序列。

3.2 利用聚类进行特征重构

聚类的基本原理是将数据分成簇,以创建具有共同特征的不同区域,这些簇具有相似的特征。因此,文中将光伏的时间序列进行聚类,分为四类,将其作为标签重新构建数据集。为了得到更全面的影响光伏出力的特征,文中分别使用K-shape、FCM以及层次聚类对光伏序列进行聚类。其流程如图5所示。

图5 聚类构造特征图

3.3 构造分位数回归模型

3.3.1 分位数回归

假设被解释变量Y受个因素X1,X2,…,Xk的影响,其分位数回归模型为

QY(θ|X)=β0(θ)+β1(θ)X1+…+βk(θ)Xk=X′β(θ)

(10)

其中,X′=[X1,X2,…,Xk]是由解释变量组成的矩阵,QY(θ|X)为在第θ个分位点下的条件分位数,β(θ)为参数回归向量,其值随着θ的变化而变化。文中构造的目标函数如(11)所示

(11)

损失函数为

ρθ(ε)=ε(θ-I(ε))

(12)

其中I(ε)为指示函数

(13)

通过指示函数对残差的绝对值赋权重,从而通过调整分位点得到β(θ)的不同参数估计,从而得到不同分位数下的回归值。

3.3.2 构造QR-Seq2seq-Attention模型

1)注意力机制

注意力机制通过算法实现对生物注意力的模拟。注意力机制实际上是一种资源分配方案,可以解决信息过载问题。注意力机制可以对输入中的特征进行加权,减少非关键特征的权重从而突出关键特征的影响。为得到相应特征变量与出力的关系,其计算原理如图6所示。

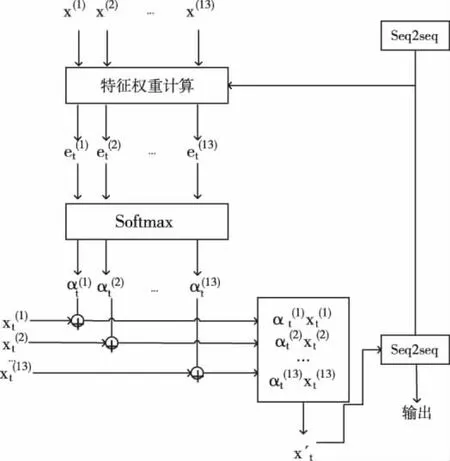
图6 特征注意力机制的编码模型

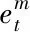
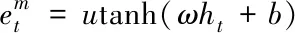
(14)

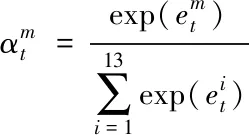
(15)

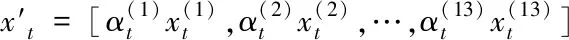
(16)

其中u和ω为权重系数;b为偏置系数。

2)构造QR-Seq2seq-Attention

图7显示了Seq2seq-Attention模型的主要架构。由Encoder的基本单元CNN,Decoder的基本单元GRU以及注意力机制组成。

图7 Seq2seq-Attention模型

CNN在特征提取方面具有良好的效果,可以实现从输入到输出的任意函数映射。卷积层的计算如式(17)所示

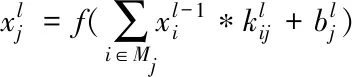
(17)

利用Seq2seq-Attention模型进行光伏出力预测的详细步骤如下:

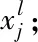
Step2:将CNN计算得到的隐藏状态与光伏出力数据传入解码器GRU层,经GRU计算得到解码器对应的隐藏向量;

Step3:计算语义矩阵,通过注意力机制的计算过程(14)-(16)计算出语义矩阵X′,从而建立相关特征与光伏出力值之间的关系;

Step4:将语义矩阵X′与解码器的隐藏向量结合起来得到光伏出力预测值。

Seq2seq-Attention模型在特征提取和短时预测上具有较好的效果,为预测不同分位数下的出力值进行不确定性分析,构造了QR-Seq2seq-Attention模型。其结构图如图8所示。

图8 QR-Seq2seq-Attention结构图

3.4 核密度估计

为得到光伏出力完整的概率密度曲线,本文采用核密度估计获得完整的概率密度曲线[14]。核密度估计是一种非参数估计方法。由于核函数具有强泛化能力,因此,将其应用于构造被解释变量分布的概率密度函数。根据条件分位数的理论,将由分位数回归获得的分位数函数作为核密度估计的输入。通过下式获得概率密度曲线

(18)

式中,n为分位数的个数,h为窗口宽度,一般由经验法计算,K为核函数,本文选择高斯核函数。计算如下

(19)

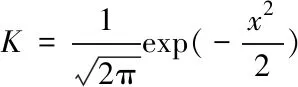
(20)

4 实验分析

4.1 实验数据及环境

算例实验数据来自全球能源竞赛公开的澳大利亚某光伏电站的数据集,采样间隔为一天,按照6:4的比例将数据分成训练集和测试集。模型的输入包括太阳辐照度等气象数据以及新构造的聚类特征数据,采用滑动窗口法对未来五天的光伏出力进行连续预测。

本实验采用的平台是Intel Core i7-10710U @ 4.70 GHz,16 GB内存。模型开发基于Python 语言编写,在Keras深度学习框架下实现。

分位数q的取值范围为区间[0.05,0.95],间隔为0.05,共19个。

本实验中,模型超参数设置如下:

表1 超参数设置

4.2 评价指标

文中从三个层面对预测的精度进行比较,包括确定性预测的指标RMSE,R2,区间预测的指标CPα和MWPα以及概率预测的指标弹球损失(Pinball Loss)。

1)均方根误差(RMSE)和决定系数(R2)用于描述模型的精度和拟合程度,RMSE的值越小证明精度越高,R2值越大证明模型拟合程度越高。其计算公式如下

(21)

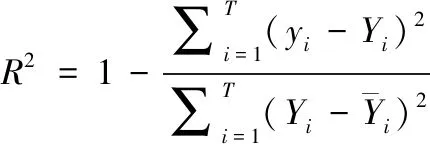
(22)

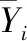
2)覆盖概率(CPα)和平均宽度百分比(MWPα)用于描述模型测值落在预测区间内的概率和间隔宽度与观察值的平均百分比。较高的CPα和较小的MWPα保证了预测间隔的有效性。其计算公式如下

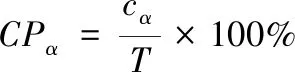
(23)

(24)

3)弹球损失(Pinball Loss)用于评估概率预测的优劣,越小证明概率预测越优。

(25)

4.3 实验结果及分析

4.3.1 异常值检测实验结果

图9显示了异常值检测的箱线图,通过计算得到光伏出力值的上下界,在界限范围外的即认为是异常值,将异常值用三次样条插值函数代替。

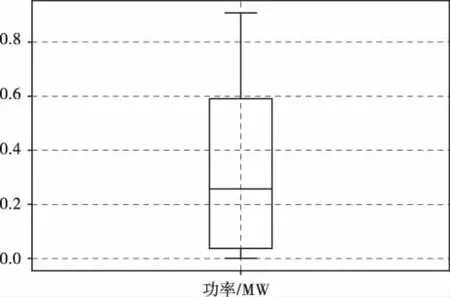
图9 异常值检测的箱线图

4.3.2 三种聚类方法预测结果比较

图10为采用三种聚类方法构造数据集进行预测与真实值的误差比较情况。事实上,三种方法都能获得较为准确的预测结果。这说明聚类方法能为光伏出力预测提供有效的信息。

图10 三种聚类构造特征的预测误差对比

表2为采用三种不同聚类方法构建数据集的预测误差比较。就三种聚类方法而言,层次聚类方法构造的数据集在确定性预测、区间预测和概率预测三个预测层位上都表现出了明显的优势,这主要是由于层次聚类的方法很灵活,可以更好的对波动性和间歇性大的光伏特征数据进行分类,从而得到特征更为准确的数据集输入到模型中进行预测。

表2 三种聚类方法评估指标比较

4.3.3 提出方法与基准模型预测效果对比

为了进一步验证模型的有效性,采用了三个基准模型QR-NN、QR-LSTM、QR-GRU与提出方法进行比较。表3显示了提出方法与三个基准模型的预测误差的定量比较结果。图11为使用各种方法进行光伏出力预测与真实值的比较情况。

表3 三种基准模型与提出方法评估指标比较

图11 与基准模型的预测误差对比

实验结果表明,提出方法在评估指标方面效果更优,其在RMSE方面相对于QR-NN、QR-LSTM、QR-GRU降低了0.19(MW)、0.14(MW)、0.05 (MW);在R2上分别提高了77%、44%、15%;在CPα上提高了56%、5%、1%;在MWPα方面表现出最小的情况。这是由于提出方法在特征提取的时间序列的预测分析方面存在着明显的优势。另外,分位数回归的间隔比较宽,这表明分位数回归获得的预测间隔是保守的,并且可以通过扩大间隔宽度来增加覆盖范围。在概率预测评估方面, QR-Seq2seq-Attention模型在预测精度方面具有明显优势,另外层次聚类的方法可以为预测模型提供更为全面和准确的信息。

由图11可知,QR-NN的方法不能有效拟合功率的变化曲线,而提出方法在平稳阶段和波动阶段均能较好的拟合实际值,表现出良好的预测性能。这证明了提出方法的有效性和可靠性。

4.3.4 KDE拟合结果

图12显示了4个未来任意时刻的太阳能概率密度曲线。由图可得,所有实际值基本都分布在概率密度曲线的中间,这进一步证明了提出方法获得的条件分位数结果进行概率分布估计的有效性。分析表明,基于Seq2seq-Attention的分位数回归的概率预测方法可以很好地描述概率密度预测曲线。

图12 时刻1～时刻4的KDE拟合结果

5 结语

本文提出了一种基于Seq2seq-Attention的用于短期光伏出力的概率密度预测方法,与现有研究方法相比具有以下特点:

1)数据预处理和聚类的方法分别提高了输入数据的质量和构建了重要的特征,分析了影响光伏功率序列的重要特征,提高了预测性能;

2)Seq2seq-Attention模型深度融合了CNN和GRU的特征提取和特征融合能力,对于波动性强的光伏出力序列有很好的预测结果,并能及时拟合出力变化曲线。

以澳大利亚光伏电站数据集进行仿真,实验数据显示提出方法在RMSE方面最高降低了0.19(MW),在CPα方面最大提高56%,在弹球损失方面最大降低0.13(MW)。结果表明,提出方法不仅得到了更加全面的特征,预测精度提高,并可为电力企业提供更加全面的信息参考。在未来的研究工作中,将聚焦于对不同预测尺度下的概率预测模型结构进行优化。