“数形”结合 构建“模型”
——《转化策略》教学实录与评析
文|陈 敏 蒋明玉(特级教师)
【教学内容】
苏教版五年级下册“转化策略”例2。
【教学过程】
一、导入
●第一组:下列计算都有什么特点?
生:分子是1,前一个分数是后一个分数的2 倍。
●第二组:下列计算都有什么特点?
生:分子是1,前一个分数是后一个分数的3 倍。
【评析:让学生从形式上感受以上分数加法的特点,从不同角度去表述,既可以激发学生探索规律的兴趣,又为学生之后探究规律提供了必要的基础。】
二、探究
1.出示例题
2.放手探究
学生通过通分的方法得到:
3.再次探究
在此基础上,引导学生画出如下的正方形图,运用数形结合的方法进一步研究。
结合图1,将“数”转化为“形”,学生很容易明白:求阴影部分的和就等于一个正方形减去空白部分的差。即:
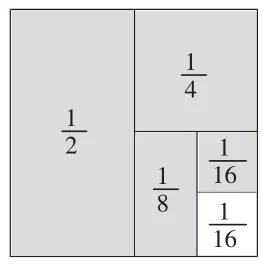
图1
师:你发现了什么规律?
生:分子是1,前一个分数是后一个分数的2 倍,求这样一组分数的和,只要用1 减去最后一个分数即可。
4.尝试运用
5.变式突破
师:下面这几道题也能用这个规律计算吗?把算式的意义画
在正方形图上。
(引导学生交流、展示,如下)
结合图2~4,灵活转化观察角度,得到新的发现:
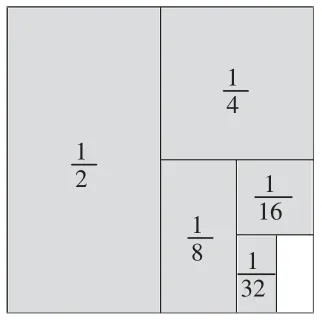
图2
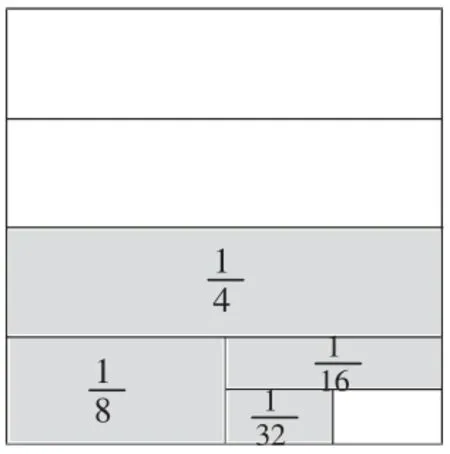
图3
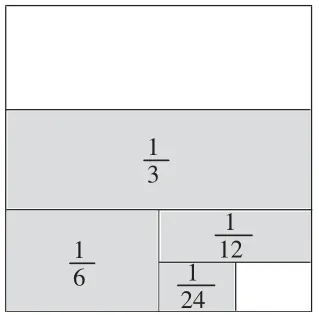
图4
6.规律推广
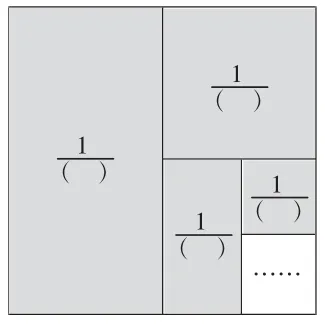
图5
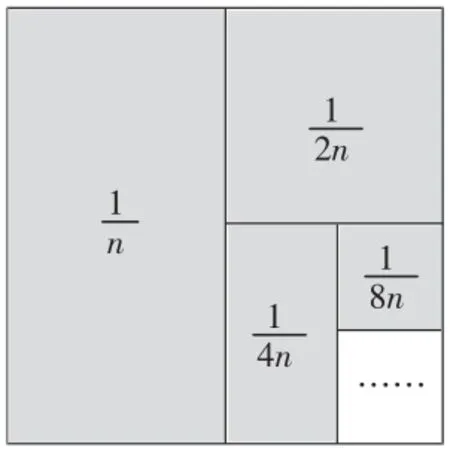
图6
在学生举例的基础上,推广并概括到普遍性规律,形成有关这类分数求和的计算模型。
根据图7,编一道前一个数依次是后一个数的2 倍,求这样一组数的和的题目,引导学生从“分数”拓展到“整数、小数”。
图7
生:8000+4000+2000+1000+500+250=8000×2-250=15750
生:3.2+1.6+0.8+0.4+0.2=3.2×2-0.2=6.2
【评析:先让学生利用数形结合的方法提出猜想:后一个数是前一个数的,其和等于用1 减去最后一个加数。然后进行验证,在验证过程中又产生新的问题,再次运用数形结合的方法,转换观察视角,深入探究,大胆提出新的猜想。最后让学生运用数形结合的方法仔细验证,进而发现了更为一般性、普遍性的规律,构建了一个数学模型:后一个数是前一个数的,其和等于第一个加数的2 倍减去最后一个加数。让学生在发现、猜想、验证中体验数学模型的形成过程,初步掌握探究数学模型的一般方法。】
三、运用
1.推广性运用
(1)128+64+32+16+8+4+2+1
(2)4.8+2.4+1.2+0.6+0.3+0.15
【评析:让学生从“分数”推广到“整数、小数”,引导学生灵活运用发现的规律拓宽思维,培养学生“举一反三”的能力。】
2.拓展性运用
利用数形结合,用正方形图来画一画(如图8、9)。第一题的和是,剩下的是;第二题的和是,剩下的是。可以发现:剩下的总比取出的多1 份。
图8
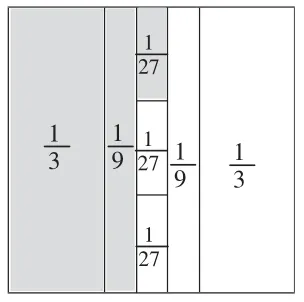
图9
3.你还能编出一些类似的算式,并且运用“数形结合”的方法发现其中的规律吗?
四、小结(略)
【评析:运用“数形结合”的方法,引导学生由2 倍的规律拓展到3 倍的规律,培养了学生思维的深刻性。最后让学生自己独立编写一些有规律的算式,既有效激发了学生探究规律的兴趣,又培养了学生独立探索、发现规律的能力,同时感受到数学规律的美妙和有趣。】
【全课评析】
史宁中先生强调:“任何一门学科都应该把培养学科直觉(或直观)作为一个根本的教育任务。数学要培养数学直观,数学的结论是‘看’出来的,不是‘证’出来的,因此培养数学直观是很重要的。”直观的培养是学生经验的积累,而不是老师说教的结果,所以要帮助学生培养基本活动经验。因此,本节课让学生充分地把算式“画”出来,引导学生将“数”转化为“形”,从而发现“计算模型”。通过题组对比,能够使学生深刻地领会到“几何直观”的作用:发现了一个规律(计算模型),而运用这个规律可以举一反三去解决更多、更复杂的相似问题。由此,不但加深了学生对“用画图找转化方法”的理解,还启发了学生在遇到复杂问题时,先用画图的方法从探索简单的问题起,发现其中的规律,然后运用所获得的规律去解决复杂的问题。
《义务教育数学课程标准(2022年版)》对“模型意识”的内涵是这样阐述的:模型意识主要是指对数学模型普适性的初步感悟。知道数学模型可以用来解决一类问题,是数学应用的基本途径。学生学习数学,不只是要记住某些规律与结论性的东西,更重要的是在学习数学的过程中领悟数学的思想方法,积累数学活动的经验。以上教学,在计算过程中发现有特点的分数加法问题,运用数形结合的方法,经历猜想与验证的过程,引导学生探索规律、发现规律和运用规律,在探索和运用规律的过程中培养学生积极探索、大胆猜想、仔细验证、灵活运用的能力。这样不断递进的猜想验证过程不仅让学生学会解决某一道题,更重要的是能让学生找到解决一类题的方法与规律,尤其是感悟了类比归纳性研究方法,并且因此修正得到更为科学完善的结论:如果前一个数(分数、整数或小数)依次是后一个数的2 倍,求这样一组数的和,只要用第一个数的2 倍减去最后一个数即可。事实上,这样丰实的猜想验证过程更符合数学教学内在的数理逻辑,不仅使“数”与“形”各展其长,实现抽象逻辑思维与具体形象思维完美地统一,也更高层次地实现了数学活动经验与数学思想方法建构以及后续“整体性”“结构性”地迁移运用,让学生后续的学习更加给力。
上述这样的拓展设计,在体验和感悟中,通过适时地概括、揭示和提炼,使隐性的数形转化思想显性化,从而被学生所认识、理解和掌握。通过运用,进一步加深对数形转化思想方法的理解和感悟,将数学思想内化为学生的数学素养。

