基于新型粒子群算法的结构动力学热振模型修正
王震宇,王计真,杨婧艺,何鹏远,潘成浩,周凌波,何成,何欢,*
1.南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016
2.南京航空航天大学 振动工程研究所,南京 210016
3.中国飞机强度研究所 结构冲击动力学航空科技重点实验室,西安 710065
4.中国船舶科学研究中心 船舶振动噪声重点实验室,无锡 214082
5.南京航空航天大学 无人机研究院,南京 210016
高速飞行器需要在热、声和机械载荷等极端组合环境中长时巡航,无法正确考虑环境/载荷、结构响应和不断变化的材料状态之间的非线性耦合是当前预测系统响应和结构寿命的主要问题[1]。高温环境对于结构振动特性的影响主要有2方面:一方面,由于材料参数随温度改变,结构本身的刚度也会随着温度的升高而降低;另一方面,结构在高温下不可避免地会在内部产生一定的热应力,因而附加的初始应力刚度矩阵会改变结构的整体刚度[2-3]。大型复杂结构通常由多组件连接构成。连接结构存在应力集中、几何或边界非线性、预紧力和摩擦等不确定因素,且在热环境下连接状态会随着线胀现象、材料软化及间隙状态等变化而变化[4]。有限元模型为理解高温环境下复杂多组件飞行器结构在各种载荷条件下的性能提供了一种方便的方法,减少动力学有限元模型的误差是成功预示结构振动响应的关键。模型修正作为利用较为准确的实验结果减少有限元模型计算误差的有效技术,已经广泛应用于航空、航天、建筑等领域。有限元模型修正方法依据修正对象的不同可分为直接修正方法和迭代修正方法[5-6]。随着计算机技术的发展,迭代修正方法因其物理意义明确、便于结合大型工程软件等优点逐渐成为主流方法。迭代修正方法的基本思路与结构优化理论相似,需要对复杂的非线性罚函数进行最小化处理[7]。
近几十年来,许多智能算法的出现极大地提高了迭代修正的效率和精度。张安平等[8]提出一种基于混合人工鱼群算法(HAFSA)的修正方法,并以GARTEURE飞机模型为例证明了该方法的可行性。He等[9]结合径向基函数(RBF)代理模型和非支配排序遗传算法(NSGA-Ⅱ)使用模型修正的方法实现了针对不同温度分布系统的热物性参数辨识。Tran-Ngoc等[10]基于正交对角化改进粒子群算法(IPSO)并应用到大型铁路桥梁模型修正中,显著降低了迭代计算成本。于开平和刘荣贺[11]提出一种多族群粒子群优化算法(MRPSO),降低了搜索陷入局部最优的概率,并将该算法成功引入模型飞行器的模型修正问题中。Yin和Zhu[12]介绍了贝叶斯神经网络(BNN)架构在模型修正中的一般设计方法,并通过对人行天桥的有限元模型修正证明了该算法的有效性。
粒子群优化算法(PSO)是一种模拟鸟群觅食行为的元启发式算法,在实际工程中得到越来越广泛的应用[13]。针对粒子群算法早熟收敛和易陷入局部最优等缺点的改进工作可以分为3个方向:①引入或优化超参数。例如,Shi和Eberhart[14-15]依次引入惯性权重和收缩因子,并比较了这2种时变参数的性能。Chatterjee和Siarry[16]在粒子群算法中使用自适应非线性变化的惯性权重,使得该算法可以在初期迭代中粗调,快速接近最优解,并在后续迭代中逐渐精调,更精确地逼近最优解。②改进粒子种群的拓扑结构和搜索策略,Al-Bahrani和Patra[17]根据适应度值将粒子群分为活性组和惰性组,采用正交对角化来替代原有的粒子更新策略,极大地提高算法的精度和速度。Zhan和Zhang[18]通过田口方法构造出新的粒子进行引导,避免了2种历史经验之间的冲突。③与其他优化算法进行融合,优势互补。Zhao等[19]将和声搜索(HS)与PSO融合为一种新的优化算法,并通过马尔可夫模型分析了其收敛性能。Zhang等[20]结合灰狼优化算法(GWO)和IPSO,得到一种混合算法。通过K-均值聚类优化实验表明该算法具有较好的优化性能和较强的通用性。
莱维飞行(Lévy Flight)是服从莱维分布(Lévy Distribution)的随机游走,其步长具有重尾分布的特点[21]。自然界中如黄蜂、驯鹿等许多生物的最佳觅食轨迹都满足莱维飞行。莱维飞行已广泛应用于布谷鸟算法(CS)等全局优化算法中[22]。在粒子群中,假设部分粒子有一定的概率失去先验的最优位置信息,此时粒子的搜索策略类似于生物觅食的随机游走行为。莱维飞行可以增强粒子群算法的全局搜索能力,Hakli和Hğuz[21]融合莱维飞行提出LFPSO算法,并在多个基准函数上证明LFPSO算法比遗传算法(GA)、差分进化算法(DE)、人工蚁群算法(ABC)以及其他粒子群变体算法搜索能力更强。在此基础上,Jensi和Jiji[23]提出的PSOLF算法在21个基准函数上的测试表现均优于标准粒子群算法、LFPSO等其他改进粒子群算法,但PSOLF算法依然没能避免传统算法中局部和全局2种引导经验之间的冲突[24],在搜索具有多个局部最优峰值的高维复杂函数时,仍然不能得到理论最优解。
本文针对高温环境复杂结构动力学问题输入输出关系复杂、多状态性、不确定性等有别于传统动力学问题的特点,提出一种基于田口试验设计和莱维飞行的新型粒子群算法——莱维正交粒子群算法(LOPSO),并应用于高温环境典型复杂多组件结构模型修正问题中。为了验证LOPSO算法的搜索能力,本文以轴系轴承-轴承座弹簧阻尼参数修正问题为例,与性能优异的PSOLF算法进行对比,验证LOPSO算法具的搜索能力。最后对比某典型结构在14、300、500 ℃温度环境下仿真模拟与实验测试的结果。在经所提出的算法修正后,结构的有限元模型精度得到了极大的提高。
1 新型改进粒子群算法
1.1 全局粒子群优化算法
全局粒子群优化算法(GPSO)用数学语言可以具体地描述为:在D维空间中,粒子群包含M个粒子。每个粒子表示优化问题的一个备选解,第k迭代步第i个粒子更新公式为
式中:vki=(vi1,vi2,···,viD),为粒子速度向量;xki=(xi1,xi2, ···,xiD),为第i个粒子的坐标位置;pki为粒子历史最优解;gk为粒子群历史最优解;°为Hadamard积;c1、c2为加速度因子,一般取值为2;r1、r2为D维的0~1之间的随机数向量;w为惯性权重因子;K为压缩因子;w、K一般设置为k的线性或非线性函数
式中:w的变化范围为[0.4,0.9],wmax=0.9和wmin=0.4;N为最大迭代总数。
将粒子群信息表示为矩阵形式可写为
式中:Xk、Vk、Pk(k=0,1,···,N)为M×D的矩阵;M为种群规模。
式(1)的搜索策略的优点是能够使粒子快速集中至极小值处,但其缺点也很明显。由于该搜索策略的数据缺乏多样性,所以算法一旦陷入极小值,则很难跳出局部最优,最终往往难以搜索到全局最优解。
1.2 粒子的莱维飞行搜索策略
假设粒子群中的部分粒子有一定的概率失去先验的最优位置信息,且此时这些粒子按照莱维飞行进行随机游走,更新公式为
式中:α为步长控制向量,与xki维度相同,其元素为0~1之间的随机数;s为步长,服从莱维分布,莱维分布常用Mantegna算法模拟
式中:β为稳定性指数,常取1.5;μ、ν服从正态分布
其中
式中:Γ为标准伽马函数。
文献[21-23]分别将莱维飞行融入不同的搜索机制以改进粒子群算法,并在21个基准函数上测试,证明莱维飞行可以对搜索空间进行深度探索,避免了粒子位置多样性的损失,增强了粒子群算法跳出局部最优的能力。然而对Rosenbrock、Rotated Schwefel等几类高维、多峰、强非线性函数,单纯引入莱维飞行机制仍然很难搜索到理论最优解。
1.3 莱维正交学习粒子群算法
本文提出一种新型的改进粒子群算法,该算法旨在利用莱维飞行的跳跃能力和田口设计的正交学习增强算法的全局搜索能力。首先介绍正交学习过程。
假设为粒子群算法中第i个粒子的3个历史经验坐标向量。田口设计以这3个1×D的向量作为水平,且以优化参数的个数D为因子数,则该D因子3水平田口设计正交表可表示为
式中:V为正交表中组合的总数;集合G中-1、0、1代表3个水平。为了清晰直观地表示出各水平元素的组合,定义函数
应用函数ϕ(x)和矩阵A将矩阵L转化为3个只有0、1元素的矩阵
式中:A的元素均为1,大小为V×D。经过田口设计后的粒子位置向量组合为
若为最小值优化问题,则令(i=1,2,···,M)中适应度最小的坐标向量为xb。再根据田口设计试验结果,运用极差分析法找出最优水平组合,其对应的坐标向量定义为xp。最后选择xb、xp中适应度值最小的向量,记为xkOi。以上过程可以记为
式中:OED代表田口设计及正交学习过程。该过程利用历史学习经验构造了一个合理的最佳经验用于指导粒子的更新。粒子仅使用一个经验来引导更新,避免了GPSO算法中2种经验之间的冲突,有利于算法更快地收敛到最优。
在莱维正交学习粒子群算法(LOPSO)中,飞行概率因子f∈(0,1],当0.5<f≤1时,将粒子当前位置xki、历史最优解pki、全局最优解gk作为田口设计的3水平;当f≤ 0.5时,xki按式(4)随机游走变为莱维飞行项Lxki,此时取Lxki、pki、gki为水平。
当k→+∞时,xki、pki、gk趋于接近,粒子不再更新,算法最终可以收敛。理想状态下有限元模型与实际模型误差函数Y最小值应为0,但这几乎是不可能的。所以设置一个阈值,当适应度值小于阈值时则认为结果收敛。若阈值设置过小时,很长时间的迭代后适应度值仍无法收敛到阈值以内,此时可通过最大迭代步数N来控制算法停止,当迭代步数达到N时亦可停止算法。LOPSO算法的具体步骤如下。
步骤1设置种群规模M、搜索维度D、最大迭代步数N、惯性权重因子最大值wmax和最小值wmin。
步骤2随机生成初始粒子群信息X0和V0。
步骤3令k=1;根据实验数据和有限元模型确定目标函数Y=F(X),F-1为其逆函数;评价初始适应度值;并令P0=X0、g0=F-1(minF(X0))。
步骤4根据式(2)计算惯性权重因子ω、压缩因子K;令i=1。
步骤5历遍种群中每个粒子,随机生成飞行概率因子f,根据其大小求XOk
步骤6更新粒子,计算公式为
式中:r为0~1间的随机数;c为加速度因子,取值2;压缩因子K、惯性权重因子w的值依照式(2)计算获得。
步骤7根据式(15)、式(16)更新历史经验
步骤8计算所有适应度值,判断是否收敛或达到最大迭代次数N,若未满足条件返回步骤4。若满足条件,则输出终步的全局最优解,即寻优结果,算法终止。
该算法的特点在于在种群计算时采用一种全新的更新策略,以唯一的最佳经验作为引导,避免了传统粒子群算法2种引导经验之间的冲突,并且飞行概率因子的设计既防止了局部收敛,又保证了算法的有效收敛。LOPSO方法流程如图1所示。

图1 LOPSO方法流程图Fig.1 Flowchart of LOPSO method
2 轴承等效弹簧阻尼参数修正
2.1 仿真算例
通过修正传动轴系轴承-轴承座等效建模的刚度和阻尼参数,简单验证上述算法的优越性。假设传动轴系通过3对轴承-轴承座与船体固接;轴的一端有一质量盘,轴之间采用联轴器相接。若仅需修正垂向等效参数,则该模型可在有限元软件MSC.Patran中简化为图2所示的梁单元模型。轴系各处材料相同,密度为7.8×103kg/m3,弹性模量为210 GPa,泊松比取0.3。质量盘和联轴器简化为对应位置节点上的附加集中质量。不考虑轴的内阻尼并将轴承-轴承座等效为一端固支的弹簧阻尼单元,则刚度系数k1、k2、k3和黏性阻尼系数c1、c2、c3即为需要修正的参数。
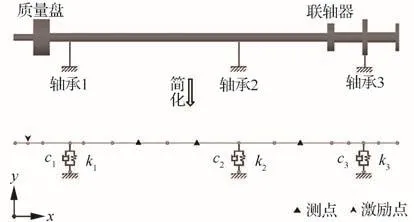
图2 轴系轴承数值算例Fig.2 Numerical example of shafting bearings
2.2 目标函数
考虑黏性阻尼,多自由度系统频域运动方程形式为
式中:ω为激振频率;M、K、C分别为总质量矩阵、总刚度矩阵、总阻尼矩阵;x为位移响应向量;f为激振力向量。对应的频响函数矩阵为
式中:HD、HV、HA分别为位移、速度和加速度复频响函数矩阵;为系统在第k自由度上施加单位激励后第i自由度的加速度响应,可以写成复数形式
式中:(ω)、(ω)分别为(ω)的实部和虚部。
频响函数同时包含了刚度和阻尼信息,共振频域的频响值主要受阻尼大小的影响,而非共振区的频响值则与刚度更为相关。因此可以采用单点激振、多点拾振的频响函数法获取轴系的动态响应特性。定义实验测量和计算响应的平均Y向加速度输出误差
假设仿真实验沿y负向加载单点单位激励,测试频段为10~2 000 Hz。则fj(ω)=1,可根据式(19)、式(20)定义目标函数Y(k1,k2,k3,c1,c2,c3)
为了模拟真实的实验状态并检验算法的抗噪声干扰能力,对仿真实验测得的加速度频响添加5%的随机白噪声。等效刚度和阻尼的修正问题可以转化为目标函数Y(k1,k2,k3,c1,c2,c3)的最小值问题,其中k1~k3为刚度系数,c1~c3为阻尼系数。
2.3 修正结果及对比
分别应用PSOLF和LOPSO算法解决上述最小值问题。为了定性地比较分析,控制各算法的总计算次数相等,最大迭代次数N取50,且将2种算法的超参数均设置为:c1=c2=c=2.0,ωmin=0.4,ωmax=0.9。表1展示了优化算法的参数设置及时间成本。图3中给出了迭代收敛曲线。可以看出当总计算数相同时,PSOLF和LOPSO方法的时间成本大致相同。前20步迭代PSOLF算法搜索得更快,后30步迭代LOPSO算法的优势逐渐体现。这是由于在迭代前期LOPSO算法中,莱维飞行项Lxki通过正交学习过程与历史最优解pki、全局最优解gk进行综合,所以粒子的更新较为谨慎。而PSOLF方法中粒子群得益于莱维飞行项快速向局部优解处聚拢。迭代后期3个引导经验的相互冲突使得PSOLF算法始终在局部优解附近徘徊。而LOPSO方法最终搜索到目标函数最小值明显优于前者的搜索结果。这表明LOPSO算法相比于PSOLF算法更不容易陷入局部优解,全局搜索能力更强。

表1 优化算法超参数设置Table 1 Optimization algorithm parameters

图3 收敛曲线Fig.3 Convergence curves
表2中比较了轴承-轴承座等效刚度和阻尼修正结果。LOPSO方法的修正值更为接近真实值,各参数误差均小于1%,而PSOLF方法修正后的参数最大误差超过6%。这进一步说明了本文所提算法搜索精度更高,可以有效应用于工程问题中。

表2 轴承等效参数修正结果对比Table 2 Comparison of updated results of bearing equivalent parameter
3 典型结构热振有限元模型修正
3.1 典型结构及有限元建模
图4给出了结构的剖面图和有限元模型。该结构分为12个部分,头部后端、二舱、三舱、四舱、尾舱、整流罩、翼面、发动机采用壳单元QUAD4和TRIA3建模;头部前端、舵面、舵面连接块、内部支架、内部质量块、整流罩连接部分以及滑块采用体单元CTETRA4建模,局部质量差用CONM2进行配平;各舱段连接部位采用加厚壳单元共节点的处理方式进行等效建模。模型材料统一为航空用钢30CrMnSiA,密度为7 750 kg/m3。

图4 结构及有限元模型Fig.4 Structure and finite element model
最终有限元模型共计66 272个单元、80 533个节点,其总质量、质心位置和转动惯量与实际模型的误差均在3%以内,可忽略不计。如图5,不同温度对应的材料热物性参数不同,因此考虑温度效的结构动力学计算是一个复杂的非线性过程。
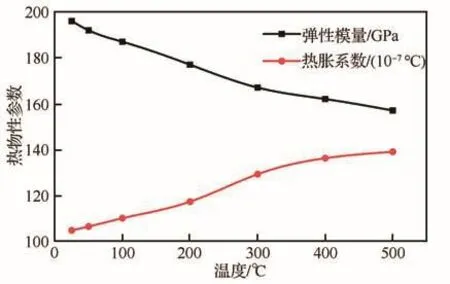
图5 30CrMnSiA热物性参数Fig.5 Thermophysical parameters of 30CrMnSiA
3.2 高温模态实验
开展地面高温模态实验,验证有限元模型的预示能力。令整流罩中面所在平面为俯仰方向,垂直于该平面方向为偏航方向。
如图6,结构通过2个弹性尼龙绳吊挂在固定横梁上,达到近似“自由-自由”的状态。尼龙绳采用绝热石棉布包裹进行保护。加热设备为环抱结构的石英灯阵,在外围包裹石棉布绝热保温,并在激振点和测点处预留小孔。实验采用单点随机激励的方式。激振器水平安装,并通过耐高温合金激振杆作用到激振点处。为了远离高温区域,力传感器安装在激振杆与激振器之间[25-26]。针对俯仰和偏航主模态在长度方向中线位置布置5个激光多普勒测振仪。测量扭转模态时分别在头部和尾部两侧各布置1个激光多普勒测振仪。测点和激振点在俯仰和偏航方向上的布置情况分别如图7、图8所示。各传感器通过数据采集器保持同步。考虑对称性,选取一个舵面进行测试。在舵面一侧布置4个激光测振仪,另一侧激励。图8中编号1、2、3、4的测点在图示局部系下坐标分别为(25,25)、(141,26)、(253,125)、(19,133);编号5处是激励点,坐标为(12,16)。

图6 高温模态实验Fig.6 Modal experiment in high temperature environment
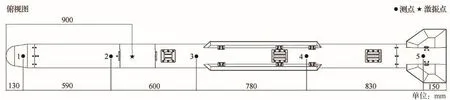
图7 测量结构俯仰模态时的测点Fig.7 Measurement points when measuring pitch modes
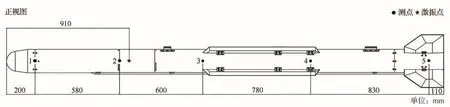
图8 测量结构偏航模态时的测点Fig.8 Measurement points when measuring yaw modes
实验测量了14、300、500 °C时的振动数据,其中14 °C为室温环境。高温实验开始前先将实验件预热至50 °C,温升速率为2.5 °C/s,达到预定温度后保温60 s。分区加热器共分为7个控温区,每个控温区在结构环向布置4个热电偶,共计28个温度测点用于测量和控制温度,保证整个结构的温度误差在足够的精度范围内。
模态实验在0~500 Hz内共获得8个主要模态,分别为:俯仰一弯、偏航一弯、俯仰二弯、偏航二弯、扭转一阶、舵面弯曲、舵面旋转、舵面扭转。采用模态置信准则(MAC)分析有限元计算模态与实验测试模态的相关性,识别出具有较高MAC值的模态对。图9给出了与实验结果匹配的模态振型云图,其中为了更清晰地显示振型,扭转振型图将翼面及舵面隐藏,舵面振型图将与其连接的结构主体部分隐藏。有限元模型和实验测量的模态振型相关度见图10。所有关键模态对的MAC值均高于0.7,说明有限元模型能够正确地获得与实验模态匹配的振型。
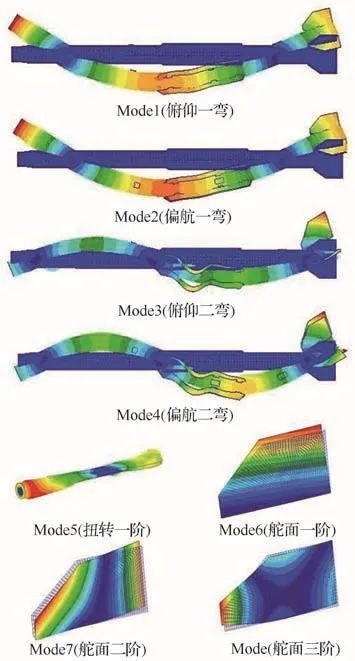
图9 主要模态振型Fig.9 Main modal shapes

图10 振型相关系数Fig.10 Correlative coefficient of mode
该结构各舱段、翼面、舵面和整流罩等部件间采用螺栓或螺钉连接,本文在建模过程中对于此类复杂连接结构直接采用共节点的方式进行简化处理。所以模型总体刚度偏大,初始有限元模型的各阶模态频率都比实验测量值高。误差主要来源于此类连接结构处的参数不确定性。
3.3 模型修正
本文建立的有限元模型的质量特性和几何特性均与实际结构的相应数据进行了核验。因此,在后续的模型修正问题中,本文假定有限元模型的质量特性和几何特性数据是可信的,无需进行修正。同时为了降低问题复杂度,本文假定材料的泊松比和热膨胀系数是可信的,仅修正材料的弹性模量参数。针对14、300、500 ℃这3种温度状态下的实验测量结果,本文暂不考虑高温下多状态的修正,分别对各温度下的弹性模量参数进行修正。弹性模量的不确定性主要表现在结构的连接部位。表3列出了8个主要连接部位的材料的弹性模量参数符号,所有材料的弹性模量初始值均为196 GPa。

表3 不确定的材料参数Table 3 Uncertain material parameters
定义基于结构模态实验的目标函数
式中:fEMAt、fFEMt分别为测量和计算的模态频率;t为模态序数;m=8。
直接用有限元模型进行迭代计算需耗费大量的计算力,因此该项研究工作借助开源的Scikit-Learn机器学习框架,构建随机森林代理模型[27]来近似修正参数和目标函数Y之间的映射关系,提高计算效率。为了降低构造代理模型的复杂度,通过灵敏度分析筛选修正变量。常见的灵敏度计算公式为
式中:xt+=(x1,x2,···,xt+Δxt,···,xn);xt-=(x1,x2,···,xt-Δxt,···,xn)。该式为有限差分法,通过对变量作微小的摄动Δxt来计算近似导数。
灵敏度计算结果如图11所示。通过灵敏度计算发现E1W、E2W主要影响舵面模态频率,灵敏度值最大;由于飞翼的弯曲模态与结构整体的弯曲模态耦合,E1R、E2R也是影响结构弯曲模态频率值的主要因素。此外E1F的灵敏度也相对较大,所以最终确定有限元模型的修正参数为E1R、E2R、E1W、E2W、E1F,共计5个。
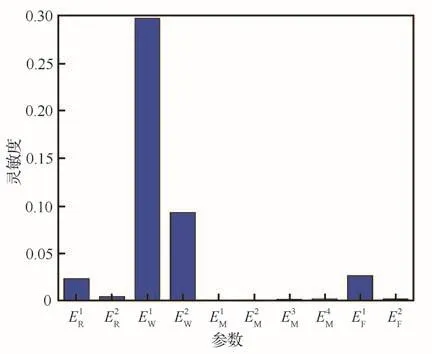
图11 参数灵敏度分析Fig.11 Parametric sensitivity
表4为结构在14、300、500 ℃下修正前后有限元模型与实验模型的模态频率比较,表中ef,b、ef,a分别为修正前、后模态频率的相对误差。
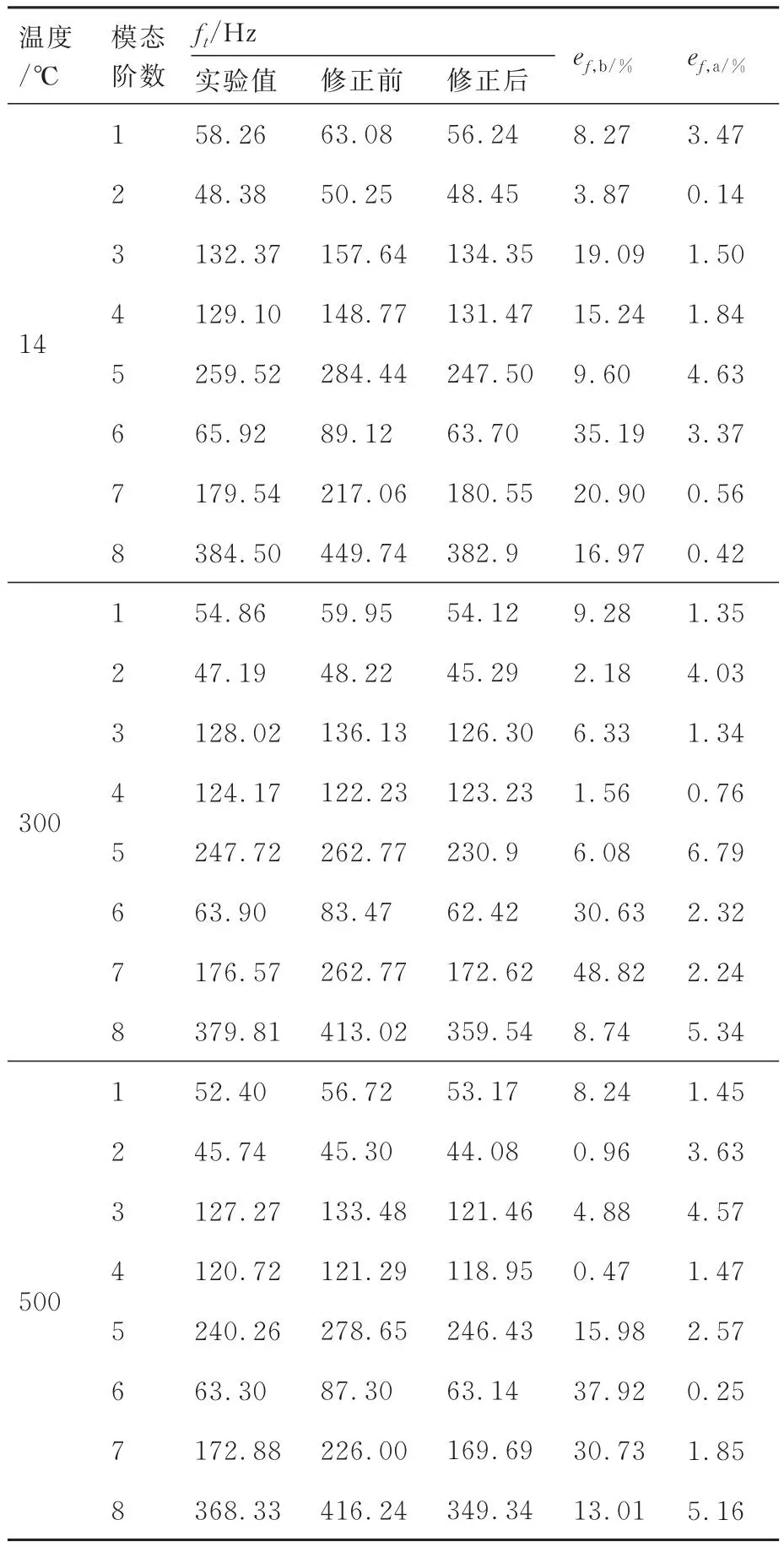
表4 实验与有限元模态对比Table 4 Comparison between measured and FEM modal results for main modes
修正前有限元模型与实验模型在频率上差异显著,室温14 ℃时频率误差最大为35.19%,300 ℃环境下最大误差为30.63%,高温500 ℃环境下频率误差最大达到37.92%。初始有限元模型的精度和可靠性值得怀疑,通过本文提出的模型修正方法进行修正后误差大幅降低,14 ℃时8阶频率的最大误差仅为4.63%,300 ℃情况下最大误差仅为6.79%,500 ℃时的最大误差仅为5.16%,动力学有限元模型精度得到提高。修正后的参数变量如表5所示。各连接部位单元的弹性模量修正值均小于初始值。这是由于连接处的等效建模导致结构的刚度过大,仅选择弹性模量作为修正参数,刚度的减小仅靠弹性模量的减小来实现,修正结果相当于局部结构的等效弹性模量。

表5 单元弹性模量修正情况Table 5 Comparison of parameters before and after modal updating
4 结论
1) 为求解复杂环境下结构动力学有限元模型修正等非线性优化问题,提出了莱维正交学习粒子群算法。该算法基于田口设计和正交学习选择最优的组合解作为唯一的更新引导,避免了传统算法中2种经验之间的冲突;同时引入莱维飞行机制增强算法跳出局部最优的能力。该新型改进粒子群算法不仅避免陷入局部最优,而且可以快速收敛获得更精确的解。
2) 轴承-轴承座等效弹簧阻尼参数修正结果表明,相比于其他先进的粒子群算法,所提出的算法搜索到的最优解最为接近真实值,精度更高。本文方法在仿真噪声的干扰的情况下,修正后刚度误差仅为0.5%,阻尼误差仅为0.3%,可以有效应用于复杂的结构动力学工程问题中。
3) 将LOPSO方法成功应用于高速飞行器热环境下的有限元模型修正。采用本文修正算法的动力学模型具有较大的预测精度,为理解工程结构在热振耦合条件下的动力学特性提供了一种可靠的方法。

