宽速域翼尖涡及其与斜激波相互作用

马印锴，李祝飞，黄琪，杨基明

中国科学技术大学 近代力学系，合肥 230026

带鸭翼的高马赫数飞行器［1-3］凭借更大的升阻比、更好的操控性和更强的机动能力［4］，在宽速域飞行过程中展现出潜力。然而，鸭翼产生的翼尖涡往往威胁其下游部件的飞行安全［5-8］。特别是在高速飞行时，鸭翼产生的翼尖涡容易与激波发生相互作用，引起翼尖涡破碎和激波变形，进而可能导致翼/舵升力下降、阻力增大，甚至诱发进气道不起动［9］等气动问题。因此，探究翼尖涡的演化及其与激波的相互作用规律成为宽速域飞行中的重要课题之一。

低速不可压缩来流中翼尖涡的研究帮助人们较早地意识到强翼尖涡对民航客机飞行安全的严重影响［10］。鉴于翼尖涡的强度与其切向速度和环量紧密相关［11］，认识这些参数的演化规律至关重要。1964年Batchelor［12］发现翼尖涡在不同流向站位处的切向速度剖面具有明显的自相似性。随后，Birch［13］、Beninati［14］和Ramaprian［15］等研究证实，翼尖涡的切向速度剖面符合Batchelor［12］提出的自相似关系式。进一步地，Grow［16］试验研究发现，翼尖涡的环量和切向速度峰值都会随着机翼展弦比和迎角的增大而增大。Mcalister和Takahashi［17］研究了来流雷诺数、机翼弦长等因素对翼尖涡环量分布和切向速度剖面的影响。Ramaprian和Zheng［18］发现翼尖涡的环量分布也存在自相似性，并给出了环量分布与翼尖涡半径的关系式。最近，Skinner等［19］通过风洞试验验证了Ramaprian和Zheng［18］给出的环量自相似关系式。切向速度以及环量分布自相似规律的发现，极大地提升了人们对不可压缩来流中翼尖涡的认知。

相对而言，超声速/高超声速来流中关于翼尖涡演化特性的研究非常有限。Smart等［20］在来流马赫数Ma∞=2.49条件下，测量了翼尖涡内部的压力分布和速度分布；Shevchenko等［21］在来流马赫数Ma∞=6条件下，对比了翼尖涡内部不同流向位置处的压力分布和温度分布。然而，超声速/高超声速来流中的翼尖涡是否也具有自相似性，却鲜见报道。

翼尖涡在激波作用下可能发生破碎，并导致飞行器性能骤降。已有的试验和数值模拟研究［22-25］主要集中于来流马赫数Ma∞=2～3，其结果表明，翼尖涡在激波作用下发生破碎时的主要特征包括激波面严重凸起变形、变形的激波下游存在亚声速回流区、局部流动出现滞止［23-24］。针对正激波诱导翼尖涡破碎现象的理论研究相对较多［26-29］，例如，Delery等［30］于1984年较早地提出了一种预测涡破碎的理论判据；Mahesh［28］进一步扩展了该预测理论的适用范围。然而，针对斜激波诱导翼尖涡破碎现象的理论研究却很少。Hiejima［26］曾提出一种理论判据，但仅在Ma∞=2～3时进行了验证。在宽速域飞行中，翼尖涡与斜激波相互作用将更加普遍，而现有的斜激波诱导翼尖涡破碎预测理论是否适用于宽速域，尚待进一步检验。

鉴于此，本文采用数值模拟方法，研究宽速域飞行过程中的翼尖涡演化特性及其与斜激波相互作用的规律，探讨宽速域条件下斜激波诱导翼尖涡破碎的理论预测方法，以期为工程应用提供参考。

1 模型及数值模拟方法

1.1 鸭翼简化构型

图1为MR2.4试验模型［31］。参考图1所示LAPCAT Ⅱ高马赫数飞行器MR2.4的鸭翼布局［31］，提炼鸭翼简化构型用于产生翼尖涡。如图2所示，该鸭翼构型呈直角梯形，展向截面为菱形，厚度为4 mm，根部弦长L=82 mm，宽度为75 mm，翼尖处的弦长为25 mm。以后缘根部顶点为坐标原点，定义流向为x方向，法向为y方向，展向为z方向。

图1 MR2.4试验模型［31］Fig.1 Test model of MR2.4［31］

图2 鸭翼简化构型Fig.2 Simplified model of canard

为模拟宽速域飞行条件，本文参考Mehta等［3］的来流参数设置，以飞行高度30 km、来流马赫数Ma∞=6为典型状态点，通过保持来流动压相等［32］，获得了来流马赫数Ma∞=0.2～6.0范围的飞行条件，如表1所示。此外，考虑宽速域飞行器的迎角变化［3］，本文研究了迎角α= 6°，9°，12°对翼尖涡演化特性的影响。

表1 模拟飞行条件Table 1 Simulated flight conditions

1.2 数值模拟方法

数值模拟采用雷诺平均的Navier-Stokes（RANS）方程求解器［33］，湍流模型采用k-ωSST（Shear Stress Transport）模型［34］，无黏通量采用Roe格式，对流项采用二阶迎风格式，黏性项采用二阶中心差分格式。空气采用量热完全气体假设（比热比γ=1.4），黏性系数采用Sutherland公式计算。

图3为计算域及边界条件，计算域采用六面体网格离散，来流参数设置与表1保持一致。鸭翼采用无滑移等温固壁条件，壁温为300 K，翼根处采用压力远场边界条件以突出单个鸭翼的流场。下游出口采用压力出口边界，其余边界均为压力远场条件。鉴于LAPCAT Ⅱ MR2.4飞行器［31］和SKYLON飞行器［3］的鸭翼与下游主翼之间的流向距离为3L～5L，将超声速工况计算域（见图3（a））的流向、法向和展向尺度分别设置为5.50L、1.46L和1.40L。如图3（b）所示，为避免亚声速扰动对翼尖涡造成影响，亚声速工况计算域的流向、法向和展向尺度分别增大至35.5L、31.5L和31.4L。

图3 计算域和边界条件设置Fig.3 Computational domain and boundary conditions setting

在超声速/高超声速来流条件下，翼尖涡与斜激波相互作用的示意图如图4所示，图中β为激波角，具体参数见2.2节。在进行翼尖涡与斜激波相互作用的数值模拟时，在图3（a）计算域的顶部边界上，根据Rankine-Hugoniot关系式［32］分别给定入射斜激波上游和下游的气流参数，则在图4中的红色虚线处将匹配出1道入射斜激波。若保持该入射斜激波的强度不变，通过设置边界条件，沿流向移动该斜激波的入射位置，可使其与不同强度的翼尖涡发生相互作用。

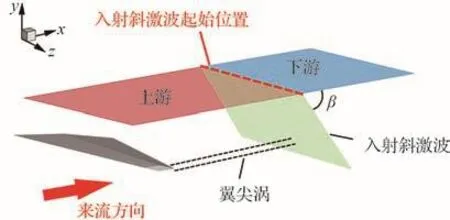
图4 翼尖涡与斜激波相互作用示意图Fig.4 Schematic of wingtip vortex/oblique shock wave interaction

表2为超声速工况采用的3套网格。如表2所示，以超声速工况为例，采用3套不同分辨率的网格考核了网格无关性，其中，Nx、Ny和Nz分别表示计算域流向、法向和展向的网格点数。为精细刻画翼尖涡结构，针对鸭翼及其下游流场附近的网格进行了局部加密，壁面y+＜1，3套网格的总网格量分别约为1.8×107、3.5×107和5.2×107。

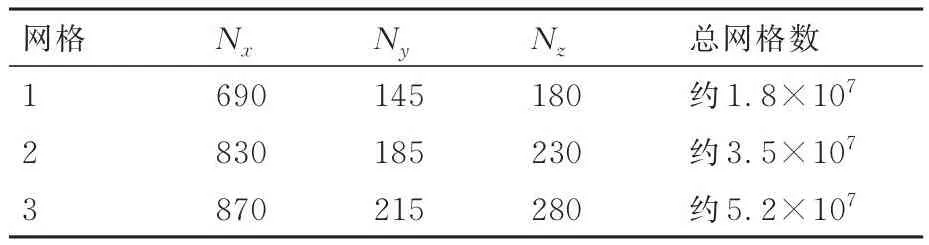
表2 超声速工况采用的3套网格Table 2 Three sets of grids used in supersonic flow

如图5所示，以来流马赫数Ma∞=2鸭翼下游无量纲流向站位x/L=2为例，提取了不同网格得到的当地翼尖涡内部静压分布曲线，其中，Ps为翼尖涡内部静压，P∞为来流静压，y/L为法向无量纲坐标。通过对比可以发现，由网格2和网格3得到的压力曲线基本重合。为提升计算效率，后续采用网格2对超声速工况进行数值模拟和流场分析。此外，针对亚声速工况，在网格2的基础上分别沿流向、法向和展向扩大计算域尺度（如图3（b）所示），其网格点分布如表3所示。

表3 亚声速工况采用的网格分布Table 3 Grid used in subsonic flow

图5 不同分辨率网格得到的压力曲线对比Fig.5 Comparison of pressure curves obtained by grids of different resolutions

为验证本文数值模拟方法对翼尖涡的刻画能力，采用Beresh等［35］在来流马赫数Ma∞=0.8、迎角α=10°条件下，通过试验得到的模型尾缘下游4.18倍弦长处的翼尖涡切向速度剖面，对数值模拟方法进行了考核。如图6所示，横坐标z/L为展向无量纲坐标，纵坐标为无量纲切向速度。对比切向速度Uθ的试验结果（图6中U∞为来流速度）和数值模拟结果可以看出，两者良好符合，表明本文采用的数值模拟方法能够可靠地刻画亚声速流动中的翼尖涡。

图6 亚声速流动中的数值模拟结果与试验结果对比Fig.6 Comparison between numerical and experimental data in subsonic flow

采用Smart等［20］在来流马赫数Ma∞=2.49、迎角α=10.4°条件下，通过试验测得的模型尾缘下游2.25倍弦长处的翼尖涡内部无量纲切向速度Mθ，考察了本文数值模拟方法对超声速流动中翼尖涡的刻画能力。图7为超声速流动中的数值模拟结果与试验结果对比，由图7可以发现，数值模拟结果与试验结果良好符合。此外，笔者前期研究工作［36-37］也表明所采用的数值模拟方法对旋涡结构的刻画是可靠的。

图7 超声速流动中的数值模拟结果与试验结果对比Fig.7 Comparison between numerical and experimental data in supersonic flow

采用Smart和Kalkhoran［23］在来流马赫数Ma∞=2.5条件下，利用29°斜劈进行的流向涡与斜激波相互作用试验，检验了本文数值模拟方法对翼尖涡与斜激波相互作用现象的刻画能力。图8为激波凸起程度的试验结果与数值结果对比。由图8可知，采用流向密度梯度云图（图8（b））显示的激波凸起位置仅比试验结果（图8（a））偏大约5%，表明本文数值模拟方法的可靠性良好。

图8 流向涡与斜激波相互作用的试验结果与数值结果对比Fig.8 Comparison of experimental and present numerical results of interaction between streamwise vortex and oblique shock wave

2 结果与讨论

2.1 宽速域翼尖涡演化特性

以来流马赫数Ma∞=6典型状态为例，图9采用流向涡量等值面显示了翼尖涡的三维结构，并以红色箭头标注了其旋转方向。本节以翼尖涡的切向速度剖面和环量分布为关键参数，分析宽速域翼尖涡的演化特性。

图9 翼尖涡三维结构（流向涡量等值面）Fig.9 Three-dimensional structure of wingtip vortex（iso-surface of streamwise vorticity）

2.1.1 翼尖涡的切向速度分布

图10为来流马赫数Ma∞=0.2～6.0、迎角α=6°时，流向站位x/L=1～5处翼尖涡的切向速度剖面。鉴于同一来流马赫数下不同流向站位的切向速度分布规律几乎一致，图10采用相同的图例表示不同流向站位，下文均采用这种简洁的标注方式。图10中：Uθ（r）为翼尖涡内部径向坐标r处的切向速度；Uθ，max为切向速度峰值；rc为翼尖涡的半径，通常取Uθ，max所在的径向坐标［35］。从图10可以看出，在低速至高超声速的宽速域范围内，不同流向站位的翼尖涡切向速度剖面均呈现明显的自相似性。作为对比，在图10中还画出了低速不可压缩流动中翼尖涡切向速度剖面的Batchelor［12］自相似关系式，其表达式为

图10 不同来流条件下的切向速度剖面Fig.10 Tangential velocity profiles at various flow conditions

式中：b=1.256 43为Lamb常数［38］。图10中的数据均与式（1）良好符合，表明超声速/高超声速流动中的翼尖涡同样遵循式（1）。

图11以来流马赫数Ma∞=6为例，在不同流向站位处（x/L=1～5）对比了迎角α对翼尖涡切向速度剖面的影响。可以看出，迎角变化对翼尖涡切向速度自相似性的影响可以忽略。

图11 Ma∞=6.0不同迎角的切向速度剖面Fig.11 Tangential velocity profiles at Ma∞=6.0 with different angles of attack

2.1.2 翼尖涡的环量分布

当0＜r/rc＜1.2时，Skinner等［19］通过试验发现低速不可压缩流动中的翼尖涡在不同流向站位处的环量Γ也具有自相似性，并通过拟合得

式中：Γ为翼尖涡内部径向坐标r处的环量；Γc为翼尖涡半径rc处的环量。

事实上，根据式（1）的翼尖涡切向速度剖面，也能够获得环量分布。由式（1）获得的环量分布曲线［12］与式（2）［19］的对比如图12所示，可以看出，两者的环量分布曲线几乎重合。

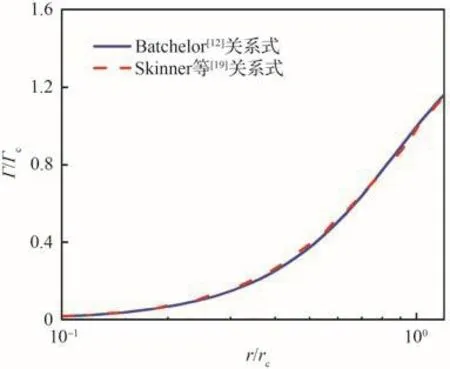
图12 环量分布曲线对比Fig.12 Comparison of circulation profiles

为检验式（2）是否适用于超声速/高超声速流动中的翼尖涡，图13给出了来流马赫数Ma∞=0.2 ～6.0范围、迎角α=6°时，流向站位x/L=1～5处翼尖涡的环量分布，并与式（2）的曲线进行了对比。可以看出，超声速/高超声速流动中翼尖涡的环量分布与式（2）均良好吻合。这表明式（2）可推广至宽速域，极大地拓展了式（2）的适用范围。

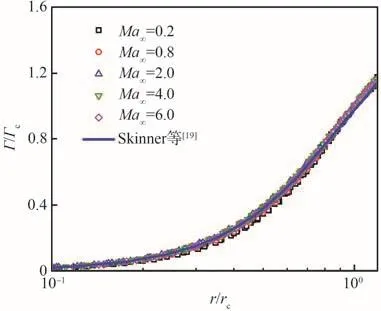
图13 不同来流条件下的环量分布曲线Fig.13 Circulation profiles at various flow conditions

图14以来流马赫数Ma∞=6.0为例，考察了不同流向站位处（x/L=1～5）迎角α对于翼尖涡环量分布自相似性的影响。从图14可以看出，不同迎角下的环量分布曲线几乎重合，表明迎角α不会改变翼尖涡环量分布的自相似性。

图14 Ma∞= 6.0条件下不同迎角的环量分布曲线Fig.14 Circulation profiles at Ma∞=6.0 with different angles of attack

2.1.3 翼尖涡旋流数

为描述宽速域条件下翼尖涡沿流向的演化，采用文献［28］定义的旋流数τ=Uθ，max/U∞衡量翼尖涡的强度。图15为来流马赫数Ma∞=0.2～6.0、迎角α=6°时，旋流数τ沿流向的变化曲线。可以看出，当来流马赫数较低时（Ma∞= 0.2，0.8），τ沿流向的变化较小，表明翼尖涡的强度相对稳定；当来流为超声速至高超声速时（Ma∞=2.0～6.0），τ沿流向迅速减小。宽速域条件下旋流数τ沿流向的变化趋势表明，当飞行器逐渐加速至高超声速时，翼尖涡强度沿流向的减弱趋势将更加明显，其对下游部件的影响也将相应地减弱。

图15 不同Ma∞下旋流数沿流向变化（α=6°）Fig.15 Variations of swirl number along streamwise direction at different Ma∞ （α=6°）

图16以来流马赫数Ma∞=6.0为例，对比了不同迎角α时旋流数τ沿流向的变化。可以看出，迎角α越大，翼尖涡越强。因此，在超声速和高超声速流动中，应重视大迎角情况下翼尖涡与激波的干扰问题。

图16 不同迎角下旋流数沿流向变化（Ma∞=6.0）Fig.16 Variations of swirl number along srteamwise direction at different angles of attack（Ma∞=6.0）

2.2 翼尖涡与斜激波相互作用

表4～表6对比了来流马赫数Ma∞=2，4，6和迎角α=12°时，翼尖涡在典型流向站位处的参数。其中：P1，c/P1，∞表征翼尖涡的压力亏损（P1，c为斜激波上游涡核处的静压，P1，∞为斜激波上游的来流静压）；U1，c/U1，∞表征翼尖涡的速度亏损（U1，c为斜激波上游涡核处的速度，U1，∞为斜激波上游的来流速度）。

表4 Ma∞=2典型流向站位处翼尖涡的物理参数Table 4 Physical parameters of wingtip vortex at typical locations in Ma∞=2 flow

表5 Ma∞=4典型流向站位处翼尖涡的物理参数Table 5 Physical parameters of wingtip vortex at typical locations in Ma∞=4 flow

表6 Ma∞=6典型流向站位处翼尖涡的物理参数Table 6 Physical parameters of wingtip vortex at typical locations in Ma∞=6 flow

从表4～表6可知，随着翼尖涡沿流向发展，其旋流数τ逐渐减弱，而P1，c/P1，∞和U1，c/U1，∞均逐渐增大，特别是P1，c/P1，∞的变化幅度更剧烈。这表明P1，c/P1，∞很可能会影响翼尖涡与斜激波的相互作用。鉴于在斜激波强度不变时，翼尖涡越强，越有可能发生涡破碎［23］。本节选取迎角α=12°工况，旨在暴露宽速域飞行过程中可能遇到的强翼尖涡情况。在来流马赫数Ma∞=2，4，6和入射斜激波的激波角β分别为60°、63°和55°工况下，分析斜激波诱导的翼尖涡破碎流场和翼尖涡不破碎流场的典型特征。

2.2.1 翼尖涡破碎流场

以来流马赫数Ma∞=2工况为例，图17为激波角β=60°、流向站位x/L=0.7处，翼尖涡与斜激波相互作用时的典型三维结构，其中，激波采用压力等值面显示，以有效地将其与剪切层、滑移线等流动现象相区分［39］；翼尖涡采用流向涡量等值面显示。从图17（a）可以看出，激波面在翼尖涡核轴线附近的凸起程度最剧烈，呈现为局部锥形凸起。为展示凸起激波面下游翼尖涡的变化，按照图17（a）中黑色箭头所示的方向，图17（b）进一步展示了下游三维流场结构。从图17（b）可以看出，翼尖涡在凸起激波面下游基本消失，表明翼尖涡与斜激波相互作用后发生了破碎。

图17 涡破碎典型三维流场Fig.17 Typical three-dimensional flowfield of vortex breakdown

图18为来流马赫数Ma∞= 2，4，6条件下，翼尖涡与斜激波相互作用流场中x/L=0.7站位处涡核轴线所在z截面的马赫数云图。可以看出，凸起激波的最前缘均出现在涡核轴线附近，且接近于1道正激波；凸起激波的下游均存在流动滞止点和大范围的亚声速区，并伴随明显的局部回流现象。这些特征，再次证实翼尖涡发生了破碎。

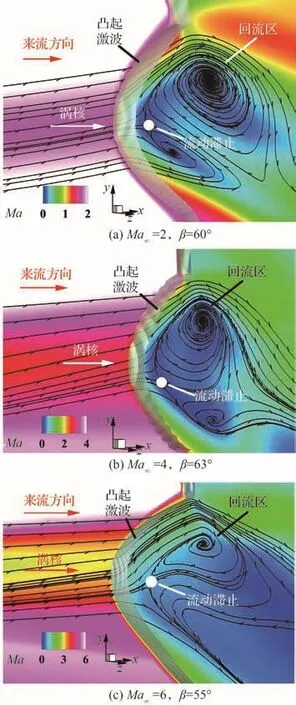
图18 涡破碎流场中涡核轴线截面马赫数云图Fig.18 Streamlines superimposed on Mach number contours near vortex core of vortex breakdown

2.2.2 翼尖涡不破碎流场

以来流马赫数Ma∞=2工况为例，图19为激波角β=60°、流向站位为x/L=4.9处，翼尖涡与斜激波相互作用的典型三维流场。其中，激波面、翼尖涡分别采用压力等值面、流向涡量等值面显示。从图19（a）可以看出，激波面在涡核轴线附近仅发生轻微凸起。图19（b）进一步展示了激波面下游的三维流场结构，可以看出，在斜激波下游翼尖涡并未消失，而是随波后气流向下偏转并继续向下游发展。这表明翼尖涡与斜激波相互作用后，未发生破碎。

图19 涡不破碎三维流场Fig.19 Three-dimensional flowfield of vortex nonbreakdown

图20为来流马赫数Ma∞=2，4，6条件下，翼尖涡与斜激波相互作用流场中x/L=4.9站位处涡核轴线所在z截面的马赫数云图。可以看出，激波面的凸起程度较小，波后虽然存在明显的亚声速区，但并未出现回流或流动滞止现象。这些特征再次证实翼尖涡没有破碎。

图20 涡不破碎流场中涡核轴线马赫数云图Fig.20 Streamlines superimposed on Mach number contours near vortex core of vortex non-breakdown

2.3 斜激波诱导翼尖涡破碎预测理论

在来流马赫数Ma∞=2～6范围内，翼尖涡与斜激波相互作用后，均有可能发生破碎（见2.2节）。现有理论［26-29］能否准确预测宽速域中斜激波诱导的翼尖涡破碎现象，是值得探讨的重要问题。

2.3.1 Mahesh预测理论

根据Mahesh［28］对翼尖涡与正激波相互作用问题的研究，翼尖涡发生破碎需满足：

式中：P为静压；ρ为密度；U为速度；1和2分别表示激波上游和下游；∞和c分别表示自由来流和涡核。在不考虑翼尖涡内部速度亏损的前提下，Mahesh［28］认为翼尖涡涡核与激波相互作用后所经历的最大压差为P2，∞-P1，c，当该压差大于其在激波前的动量通量ρ1，cU21，c时，涡核处的气流将在激波后出现局部流动滞止，进而导致翼尖涡发生破碎。所以式（3）两边取等号时，即为翼尖涡发生破碎的临界条件。

为便于对涡破碎进行理论预测，Mahesh［28］假设旋涡内部总温均匀分布，根据上述临界条件推导了翼尖涡恰好发生破碎时的临界旋流数τcri与自由来流马赫数Ma1，∞以及入射斜激波的激波角β之间的关系式为

需要注意的是，Mahesh［28］并未对式（4）能否准确预测斜激波诱导涡破碎现象进行检验。若事先已知自由来流马赫数Ma1，∞和入射斜激波的激波角β，则可以得到临界旋流数τcri。将翼尖涡的旋流数τ与临界旋流数τcri进行比较，若τ＞τcri，翼尖涡将会发生破碎。

为考察Mahesh［28］理论预测的准确性，本文在来流马赫数Ma∞=2，4，6条件下，对翼尖涡与斜激波相互作用现象进行了数值模拟，入射翼尖涡位置的变化范围为x/L=0.7～4.9（见表4～表6）。其中，Ma∞=2时，斜激波激波角的变化范围为β=37°～60°；Ma∞=4和6时，斜激波激波角的变化范围为β=30°～63°。本文数值模拟翼尖涡是否破碎的结果与Mahesh［28］预测理论式（4）的对比如图21所示。图中黑色实线表示式（4），该实线上方的区域表示发生涡破碎；该实线下方的区域表示不发生涡破碎。可以看出，Mahesh［28］理论的预测结果倾向于翼尖涡更容易破碎，这与本文的数值模拟结果不完全符合，表明该理论存在局限性。

图21 涡破碎理论预测Fig.21 Theoretical prediction of vortex breakdown

2.3.2 Hiejima预测理论

根据Hiejima［26］对斜激波诱导翼尖涡破碎问题的研究，翼尖涡发生涡破碎至少需要满足式（5）或式（6）之一。

式中：Maθ=Uθ，max/s，s为当地声速。假定翼尖涡与斜激波无相互作用，则来流和涡核处气流跨过斜激波产生的压差分别为P2，∞-P1，∞和P2，c-P1，c。根据式（5）可知，当两者之间的差量ΔP大于斜激波下游气流的动压（U2，∞为斜激波下游气流速度）时，翼尖涡将发生破碎。根据式（6）可知，若翼尖涡与斜激波相互作用前Maθ＞1，则翼尖涡会发生破碎。所以，翼尖涡发生破碎的临界条件分别为

事先通过数值模拟容易得到无斜激波入射时当地翼尖涡的Maθ。在本文来流马赫数Ma∞=2～6范围内的翼尖涡（见表4～表6），其Maθ始终＜1，均不满足式（6）。因此，本文主要关注式（5） 能否准确预测涡破碎。

为便于使用Hiejima［26］预测理论以及与Mahesh［28］理论（见2.3.1节）进行对比，本文参考Mahesh［28］的推导过程，将式（10）转化为τcri与Ma1，∞、β之间的关系式。首先，采用P1，∞对式（10）两边做无量纲化，整理可得

然后，根据Mahesh［28］的假设，认为旋涡内部总温均匀分布，得到P1，c/P1，∞与τcri的关系式为［28］

最后，在不考虑翼尖涡内部速度亏损的前提下，根据Rankine-Hugoniot关系式［32］，可得

再结合式（13），将式（12）转化为

式（16）可表示为图21中的蓝色实线，该实线上方的区域表示翼尖涡发生破碎；该实线下方的区域表示翼尖涡不破碎。从图21可以看出，Hiejima［26］理论式（16）的预测结果倾向于不发生涡破碎，这与本文的数值模拟结果不相符；同时，也表明在宽速域范围，该理论难以准确预测斜激波诱导的翼尖涡是否会发生破碎。

2.3.3 修正的预测理论

由上述分析可知，Mahesh［28］理论和Hiejima［26］理论均难以在宽速域范围准确预测斜激波诱导的翼尖涡破碎现象。结合2.2节的分析以及表4～表6可以看出，当来流马赫数和入射斜激波强度保持不变时，翼尖涡涡核处的压力亏损越剧烈，则翼尖涡越容易发生破碎。然而，Mahesh［28］理论和Hiejima［26］理论均未考虑压力亏损的影响，因此，有必要对其进行修正。鉴于Hiejima［26］理论本身就是针对斜激波诱导翼尖涡破碎问题而提出的，因此在其基础上恰当地引入压力亏损的影响，进一步挖掘潜力，很有可能获得更加准确的预测理论。

本文采用翼尖涡压力亏损值P1，c/P1，∞修正Hiejima［26］理论式（5）的左端项，修正后的预测理论为

当式（17）成立时，翼尖涡将发生涡破碎；反之，则翼尖涡不破碎。换言之，式（17）取等号时，即为修正后翼尖涡发生破碎的临界条件。式（17）两边取等号后，再同时除以P1，∞进行无量纲化，整理可得

为便于使用修正后的预测理论，采用与

2.3.2 节相同的推导思路，将式（18）转化为

类似地，可将式（19）表示为图21中的红色实线，该实线上方为翼尖涡发生破碎的区域，下方为翼尖涡不破碎的区域。从图21可以看出，在宽速域范围，修正理论的预测结果与本文的数值模拟结果均良好吻合。可见，考虑翼尖涡压力亏损的影响，并用于修正Hiejima［26］原有的预测理论，能够大幅提升其对斜激波作用下翼尖涡是否破碎的预测能力。这一发现，对于掌握翼尖涡与斜激波相互作用的规律，具有重要价值。

3 结论

本文在宽速域范围研究了翼尖涡的演化特性，分析了翼尖涡与斜激波相互作用的流场，并探讨了斜激波诱导翼尖涡破碎的预测理论，主要得到以下结论：

1）在宽速域范围（来流马赫数Ma∞=0.2～6.0），翼尖涡不同流向站位的切向速度剖面和环量分布仍然遵循低速流动中的自相似规律，并且迎角对这种自相似性的影响可以忽略。

2）相比于亚声速来流，在超声速来流中翼尖涡强度沿流向减弱地更快；随着迎角增大，翼尖涡增强，但其强度沿流向的减弱速度变化不明显。

3）通过引入涡核处压力亏损的影响，对现有斜激波诱导翼尖涡破碎理论进行修正，大幅提升了其在来流马赫数2～6范围内预测涡破碎的能力。

鉴于斜激波诱导翼尖涡破碎现象的复杂性，未来需在宽速域范围，尤其是高马赫数来流中，开展精细的试验研究。