拟合精度约束下航发叶片在机测量采样策略

2023-06-28 09:12:40万能庄其鑫郭彦亨常智勇王道

航空学报 2023年7期

万能，庄其鑫，*，郭彦亨，常智勇，王道

1.西北工业大学机电学院，西安 710072

2.中国航发南方工业有限公司，株洲 412002

航空发动机叶片是材料难切削、结构刚度弱和设计精度要求高的零件。为保证其日益增高的加工精度和效率要求，自适应加工技术成为叶片类零件精密加工的迫切需求。其中，在机测量是加工过程中识别工件当前真实形状的关键技术，能够在不卸装夹条件下检测零件上测量点位置得到工件的形状［1］。识别到工件真实形状后要能用于后续补偿加工，因此，不同于三坐标测量机只需评价检测结果是否符合设计公差的要求［2］，在机测量是需要依据离散检测结果拟合工件的实际形状。拟合工件形状的精度不仅取决于拟合方法，还与测量点采样策略密切相关。一般地，采样点数量越多，拟合工件的形状就越准确，对此，RENISHAW公司率先开发出了扫描式测头，每秒可采集1000个数据点，具有高精度、高效率等特点［3］。该测头依赖复杂的专用软件和机床配置，购置和应用成本很高，不利于在当前航空发动机制造企业中推广。但航发制造企业中大多数机床上都配有机械触发式测头，如何利用好现有的触发式测头，准确测量和拟合叶片形状更具有现实应用价值。

为了评价航空发动机叶片复杂曲面，其测量被简化为沿积叠轴方向测量一组截面轮廓线。国内高校学者针对叶片曲面测量开展了一系列的研究，卜昆等［4］研究了均匀采样、曲率采样、弦公差采样和曲率-弧长采样等方法对涡轮叶片型线上特征参数计算精度的影响。Zhao等［5］将自由曲面的检测简化为对一些截面线的测量，采用B样条曲线来逼近检测的截面线，并将构建B样条曲线所需的数据点作为测量点，通过多个拟合案例验证了所提方法的有效性。蔺小军等［6］针对薄壁叶片型线测量点分布不均问题，提出了一种测量点分区域采样方法，在测量点规划时考虑了叶片型线上前后缘和叶盆、叶背过渡区域加工误差的分布情况。于红英等［7］开发了叶片测量仪专用软件，集成了叶片上型线的拟合、偏置和匹配等功能。王进［8］采用三次 NURBS 曲线拟合叶片上规划的测量点与理论点，分别生成测量轮廓曲线和理论轮廓曲线，该方法已用于实际的叶片轮廓曲线拟合和匹配。这些研究工作为规划叶片上测量点分布提供了优化依据。

测量点的疏密直接影响在机测量的效率和拟合测量曲线的精度，对此许多国内外学者进行了研究。赵世田等［9］研究了三维型值点数据的B样条曲线重构技术，在设定逼近误差的要求下迭代计算出最终关键点和控制顶点。Sarkar和Menq［10］提出了曲线测量过程中自动控制测量点数量的算法，通过最小二乘拟合得到光滑参数曲线和实体模型上的合理测量点。Luche和Morken［11］提出了一种减少B样条函数节点数的方法，以限定样条函数的扰动偏差在给定容差内来缩减拟合曲线的数据点。Liu等［12］开发了一种基于较少测量点重建叶片曲面的算法，该方法在考虑叶片型面的设计信息和曲率连续性的情况下，使用B样条曲线重构获得高质量的曲面模型。上述文献重点分析了测量点采样策略对拟合精度的影响规律，侧重于拟合算法的改进研究，但没能揭示在机测量中测量点采样影响拟合误差的量化关系。

综上所述，基于在机测量结果拟合工件截面轮廓的几何形状会引入拟合误差。通常，测量点个数越多，工件形状拟合精度就越高，但同时可能造成部分测量点冗余，会降低在机测量检测效率，占用机床切削时间。因此，以叶片在机测量工艺规划为研究对象，定量分析了测量点分布对拟合误差的影响规律，提出了一种考虑拟合精度的航空发动机叶片在机测量采样策略，在给定拟合允差的前提下最小化测量点数量。最后基于检测离心式叶轮验证了该方法的可行性和有效性。

1 在机测量系统中误差源分析

1.1 核心概念定义

航空发动机叶片类零件在机测量前，通常在叶身设计曲面上规划若干截面轮廓线，测量点分布在这些截面轮廓线上［13］，如图1（a）所示。在这些轮廓线上布置测量点时，常用的采样方法有等弦高差法、等参数法、等步长法和自适应采样法等［14］。在工件切削结束后，依据叶片理论设计曲面上规划好的测量点，测量得到轮廓上离散的检测结果。通过拟合这些检测结果得到截面轮廓线，进一步拟合截面轮廓线获取叶片曲面，拟合的叶片曲面可作为优化后续加工工艺的依据，如图1（b）所示。

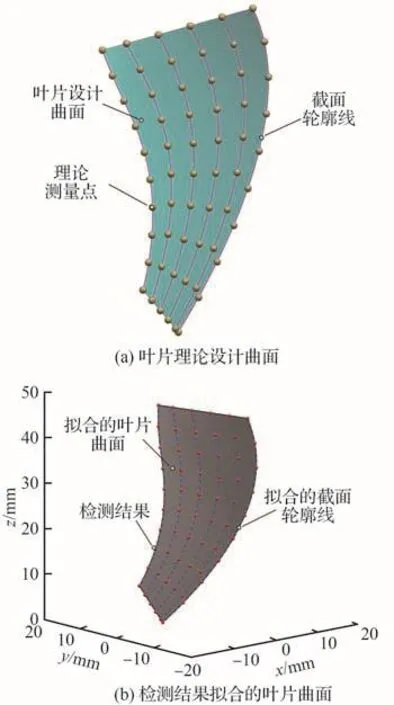
图1 叶片曲面降维成一组截面轮廓线Fig.1 Blade surface reduced to a set of section profile curves

三坐标测量机工作环境稳定且本身机械结构精度高，因此其检测结果是工件实际形状的参考值，可以认为不包含测量误差。为了后续分析在机测量系统中的拟合误差，先给出如下定义：

理论设计曲线：构建叶身理论设计曲面所依赖的一组平面轮廓曲线，记为Cd(t)，t∈[0，1]。

实际加工曲线：加工后叶身上真实的轮廓曲线，记为Cp(t)，该曲线是叶身工件截面轮廓的真值，但无法精确获取。

理论测量点拟合曲线：在叶片理论设计曲线上按照步长h采样，得到理论测量点集合，拟合该测量点集合得到曲线Ch(t)。

在机测量点拟合曲线：使用在机测头检测理论测量点获得在机测量检测结果，基于检测结果拟合得到的曲线Cf(t)。

三坐标测量点拟合曲线：依据理论测量点使用三坐标测量机检测，基于三坐标测量机检测结果拟合获得的曲线Cs(t)，作为实际加工曲线的参考值。

理论测量点、在机测量检测结果、三坐标测量机检测结果和各拟合曲线示意图见图2。

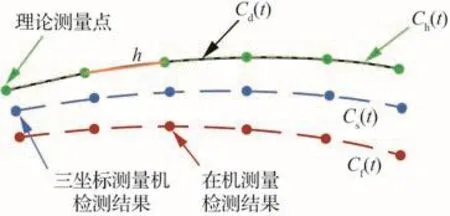
图2 测量点集、理论设计曲线和各拟合曲线示意图Fig.2 Diagram of measurement points， nominal design curve and each fitted curve.

在拟合上述理论点和检测结果时均选用三次准均匀B样条曲线［15］，该样条曲线的参数域为t∈[0，1]，参数表达式为

式中：r(t)为参数t的k次分段多项式；Ni，k(t)为B样条曲线的基函数；Vi为样条曲线的控制顶点。

1.2 拟合误差计算及误差关系建模

为了评价拟合曲线的拟合精度，提出一种拟合误差的计算方法，以图3为例阐述具体计算思路。

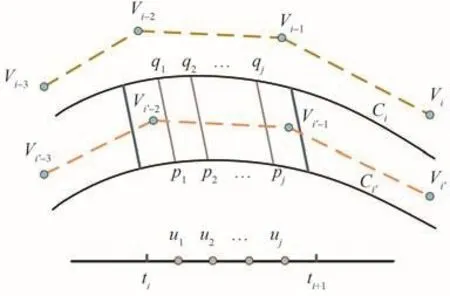
图3 两样条曲线间拟合误差计算原理Fig.3 Calculation principle of fitting error between two splines.

在节点矢量区间[ti，ti+1]内采集若干节点

ui(i=1，2，...，j)，通过采集的节点在样条曲线段Ci上取出对应的点集为qi，样条曲线段Ci′上的点集为pi，则曲线Ci和Ci′在节点矢量区间[ti，ti+1]内的拟合误差ε可表示为

叶片铣削后的实际加工曲面与理论设计曲面之间存在加工误差，该误差无法通过测量手段准确获取。此外，在机测量时检测结果中又会引入测量误差。因此与理论测量点相比，在机测量结果中包含了加工误差和测量误差。进一步，拟合在机测量检测结果时还会引入拟合误差。对于1.1节中定义的各曲线，相互之间的误差关系模型如图4所示。

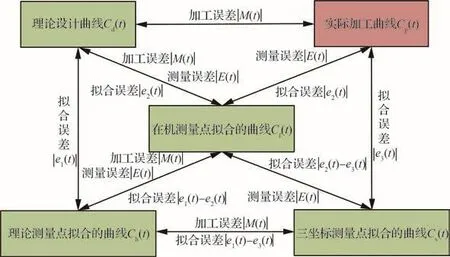
图4 各拟合曲线间的误差关系模型Fig.4 Error relationship model between fitted curves

分析该模型能够得到如下结论：

结论1由于叶片上实际加工曲线Cp(t)无法获得，因此无法建立与实际加工曲线相关的误差等式。

结论2在机测量点拟合曲线Cf(t)和理论设计曲线Cd(t)之间存在加工误差、测量误差和拟合误差。这些误差源耦合并作用于拟合曲线Cf(t)上，造成在机测量结果的拟合误差|e2(t)|无法直接计算。

由上述两个结论可知，在机测量结果的拟合误差无法直接计算，但通过对在机测量系统中多源误差的参数化建模，能够建立在机测量结果的拟合误差上界模型［16］。在本文中，以逼近程度评价拟合曲线与理论设计曲线之间的相似性，以相似程度评价两拟合曲线之间的相似性。

2 截面轮廓的在机测量拟合误差建模

2.1 在机测量拟合误差建模流程

由1.2节中结论可知，加工误差、测量误差和拟合误差等误差源相互耦合，造成在机测量拟合误差无法直接定量计算。借鉴放缩变换的思想［17］，将等式问题转化为不等式问题，利用不等式的传递性，在耦合误差源中通过不等式变换消除加工误差和测量误差，进而构建在机测量拟合误差上界模型。进一步，依据有限元理论中离散逼近误差原理构建拟合误差上界模型与采样步长之间关系，进而得到由采样步长表示的在机测量结果拟合误差上界等式，通过判断拟合误差上界值是否满足设定的拟合允差量迭代计算出最少的采样点个数，具体的计算流程如图5所示。

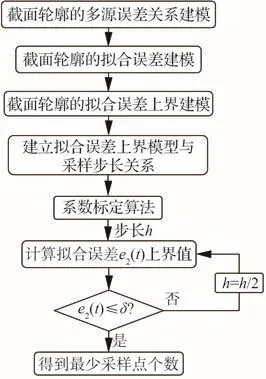
图5 最少测量点数量计算流程Fig.5 Flowchart of calculating the minimum number of measurement points

2.2 在机测量拟合误差上界建模

由1.2节中结论1可知，由于表示截面轮廓线真值的实际加工曲线Cp(t)不能精确获得，根据图4中各类曲线间存在的误差关系可归纳出理论设计曲线、理论测量点拟合曲线、在机测量点拟合曲线和三坐标测量点拟合曲线之间的误差等式，在机测量拟合误差上界的建模过程如下：

1）截面轮廓的在机测量中多源误差关系建模

2）截面轮廓的拟合误差建模

由于工件切削过程中的加工误差|M(t)|无法准确获得，同时与在机测量误差|E(t)|、拟合误差等误差项相耦合。因此，需要基于上述误差等式消除加工误差项和测量误差项，得到仅含有拟合误差项的等式，计算结果为

3）截面轮廓的拟合误差上界建模

根据1.2节中结论2和式（9）～式（12）可知，截面轮廓的拟合误差建模得到的等式关系中包含了理论测量点、在机测量结果和三坐标测量机结果拟合误差，无法获得仅含有在机测量结果拟合误差项的等式。但可以构建在机测量拟合误差的上界模型，以此分离出在机测量结果拟合误差。基于放缩变换思想先对式（11）右边的拟合误差进行两次变换，则有：

将式（6）代入式（13）中，式（13）可重写为

则测量误差|E(t)|可变换为

式（8）转变为|e3(t)|=|Cd(t)-Cs(t)|-|M(t)|，再结合式（9）对式（12）中右边项进行变换，具体过程为

进一步，加工误差|M(t)|可变换为

最后，由式（4）表示出在机测量拟合误差|e2(t)|，并结合式（15）和式（17）进行变换，得到在机测量拟合误差|e2(t)|的上界为

2.3 建立拟合误差上界模型与采样步长关系

在机测量拟合误差上界表达式由理论设计曲线、理论测量点拟合曲线、在机测量点拟合曲线和三坐标测量点拟合曲线相互间的误差项共同表示。依据有限元理论中离散逼近误差方法［18］以及1.2节中逼近程度、相似程度的定义，建立两样条曲线间误差与采样步长之间的关系：

式中：h为参数域内的步长；P为拟合曲线的次数；C1为由理论测量点拟合曲线Ch(t)向理论设计曲线Cd(t)的逼近程度；C2为由在机测量点拟合曲线Cf(t)向理论设计曲线Cd(t)的逼近程度；C3为由三坐标测量点拟合曲线Cs(t)向理论设计曲线Cd(t)的逼近程度；C4为在机测量点拟合曲线Cf(t)和三坐标测量点拟合曲线Cs(t)间的相似程度；C5为三坐标测量点拟合曲线Cs(t)和理论测量点拟合曲线Ch(t)间的相似程度。

因此，在机测量结果拟合误差|e2(t)|上界与采样步长之间的关系为

2.4 拟合误差上界模型中系数标定算法

由2.3节可知，在机测量拟合误差上界值可进一步采用步长和系数表示，式（20）中各个系数值均可采用系数标定算法计算得到，以计算C1值为例，该算法具体的实施步骤为

步骤1给定初始步长h=ha，依据等步长法和h在理论设计曲线Cd(t)上采样一组点集Θn；对于在机测量和三坐标测量机检测时，需要先根据经验值设定一个初始小步长hmin，离散得到一组密集的测量点［19］，使用在机测量和三坐标测量机一次检测所有采样点获得检测结果，此时再根据步长h=ha在检测结果中取出对应的测量点集合。

步骤2拟合采样点集Θn得到理论测量点拟合曲线Ch(t)；当计算系数C2-C5，涉及到在机测量点拟合曲线Cf(t)和三坐标测量点拟合曲线Cs(t)时，需要分别拟合在机测量检测结果和三坐标测量机检测结果得到对应的曲线。

步骤3计算样条曲线Ch(t)与Cd(t)之间的二范数表示为

式中：a、b为参数域内节点矢量区间；M为节点个数，由步长h和三次准均匀B样条曲线性质决定。

步骤4令式（21）中积分函数等于f(t)，则式（21）变为

步骤5选择4节点的高斯积分［20］，对应的高斯积分点值和权重如表1所示，将式（22）中一般定积分问题转化为高斯积分问题，得到：

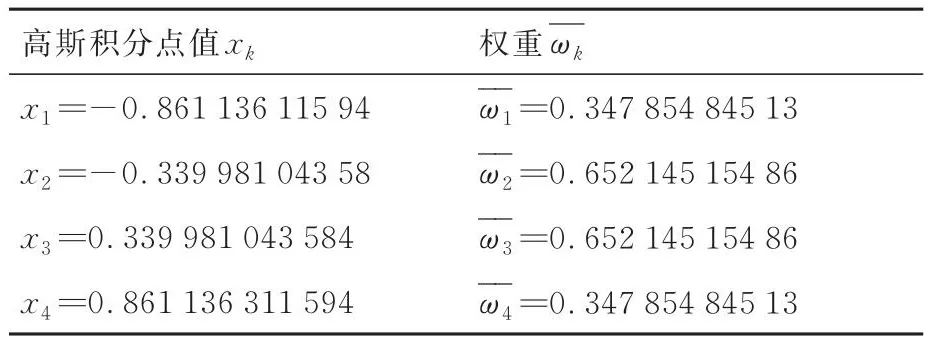
表1 高斯积分点值和权重Table 1 Gaussian integral points value and weights

步骤6将［-1，1］区间内的高斯积分点转换到样条基函数的节点矢量区间[a，b]内，故当积分节点数目为4时，有：

对于积分区间[a，b]，用线性变换将积分区间由[a，b]变成［-1，1］，根据可得：

将uk、ωk代入式（23）中得到：

则式（22）可以表示为

步骤7对等式|Ch(t)-Cd(t)|=C1·hP+1两端取对数，得到：

式中：设y=ln|Ch(t)-Cd(t)|，x=lnh，c=P+1，d=lnC1，则式（28）表示为y=cx+d，解出对应的系数值C1。

按照上述步骤可以得到系数C2～C5值，进一步计算得到在机测量结果拟合误差|e2(t)|的上界值。在规划测量工艺时，为了保证拟合曲线的连续几何形状，根据叶片的制造公差带指定在机测量结果拟合允差量［19］，记为δ，则根据式（29）可进行在机测量结果拟合允差量的判定。若符合条件，则对应的步长满足要求；反之步长取h=h/2 （对于在机测量点拟合曲线和三坐标测量点拟合曲线，需要根据变换后的步长在获得的检测结果中重新取出对应的测量点），重复执行步骤 1～步骤 7并结合式（29）进行拟合允差量的判定，直至符合精度要求。

3 实验验证与分析

借助本文提出的方法以测量某型号离心式叶轮上6个叶片为例验证其有效性，具体的实验规划流程如图6所示。实验中使用的主要设备有RENISHAW OMP 40-2小型高精度触发式测头、北京精雕JDGR200_A10H型五轴机床和蔡司CONTURA 7106型三坐标测量机。

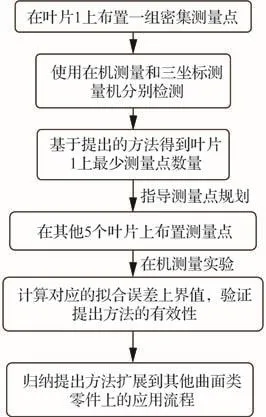
图6 实验验证流程Fig.6 Experimental verification process

3.1 叶片1实验规划与流程

根据2.4节中系数标定算法可知，在测量前需要在叶背的一条样条曲线上设置初始小步长，取步长h=0.006 25，布置161个测量点，如图7（a）所示，其部分理论坐标如表2所示。为了获取叶轮加工后的实际形状，需要先用三坐标测量机测量规划的测量点，如图7（b）所示，部分测量点的三坐标测量机检测结果如表3所示。

表2 叶片1上初始步长下测量点理论坐标Table 2 Nominal coordinates of measuring point under initial step on blade 1

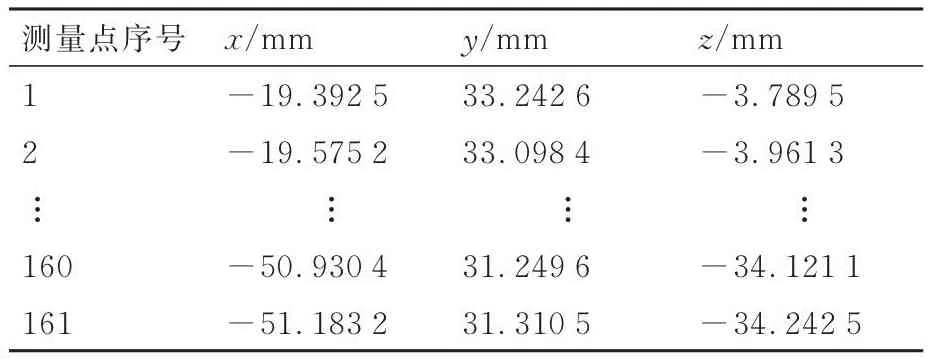
表3 叶片1上初始步长下测量点的三坐标测量机检测结果Table 3 CMM inspection results of measuring point under initial step on blade 1

图7 叶片上测量点规划和三坐标测量机检测过程Fig.7 Measuring point planning on blade and CMM inspection process

在机测量过程中，为了避免机床旋转轴发生突变以及测头与工件发生干涉，规划探针轴向时需要保证旋转轴安全、平稳的转动［21］。实验前，使用直径19.999 7 mm的标准球对在机测头进行校准，校准数据用于补偿在机测量检测结果，校准过程如图8（a）所示，对叶片1上161个测量点重复测量10次，取均值作为最终检测结果，其在机测量现场如图8（b）所示。对于直径为120 mm的离心式叶轮上叶片，其叶背制造公差带［22-23］一般为0.06～0.1 mm，设定在机测量结果的拟合允差量［19，24］为0.02 mm，则在机测量拟合误差上界值迭代计算过程如下：

图8 测头标定和叶片测量现场Fig.8 Probe calibration and blade measurement site

1）取步长h=0.2，在理论设计曲线上采样6个理论测量点，根据2.4节中步骤1及步长分别在初始的161个三坐标测量机检测结果和在机测量检测结果中取出对应的6个测量点坐标，对拟合误差上界模型中各曲线进行拟合，并求解系数C1～C5，由式（29）计算得到在机测量拟合误差上界值为0.064 3 mm，不满足在机测量结果拟合允差量0.02 mm的要求，减小步长再次迭代。

2）取步长h=0.1时共11个测量点，取出在机测量和三坐标测量机检测结果中对应的11个测量点坐标，用于拟合各曲线并求解出在机测量拟合误差上界值为0.028 8 mm，大于在机测量结果拟合允差量0.02 mm。进行下一次迭代，迭代步长h=0.05。

3）采样21个理论测量点，分别在三坐标测量机和在机测量检测结果中取出对应的21个检测点坐标用于拟合各曲线，计算得到的在机测量拟合误差上界值为0.018 6 mm，满足在机测量结果拟合允差量0.02 mm的要求，停止迭代。

因此，21个测量点为在满足拟合允差、保证测量工艺效率下的最少测量点数量。不同测量点数量下的在机测量拟合误差上界值如图9所示。

图9 不同采样点个数下的在机测量拟合误差上界值Fig.9 Upper bound of fitting error of on-machine measurement with different number of sampling points

3.2 叶片1计算结果分析

不同采样点数量下各曲线间的误差值如表4所示。在此案例中，步长h=0.05与步长为0.2、0.1时相比，理论设计曲线Cd(t)与理论测量点拟合曲线Ch(t)间误差值降低，小于0.3 μm，两曲线具有较高的重合度。而在机测量点拟合曲线Cf(t)、三坐标测量点拟合曲线Cs(t)与理论设计曲线、理论测量点拟合曲线间误差值均增大，这是由于随着采样点个数增加，计算拟合误差时引入的在机测量和三坐标测量机检测误差增大而造成的。但伴随着步长的减小，由曲线间误差和步长二者综合表征的在机测量结果拟合误差上界值减小。当迭代计算出的在机测量结果拟合误差上界满足设定的拟合允差时，既能够保证在机测量结果拟合曲线的连续几何形状，同时测量点数量最少，有利于提升检测效率。

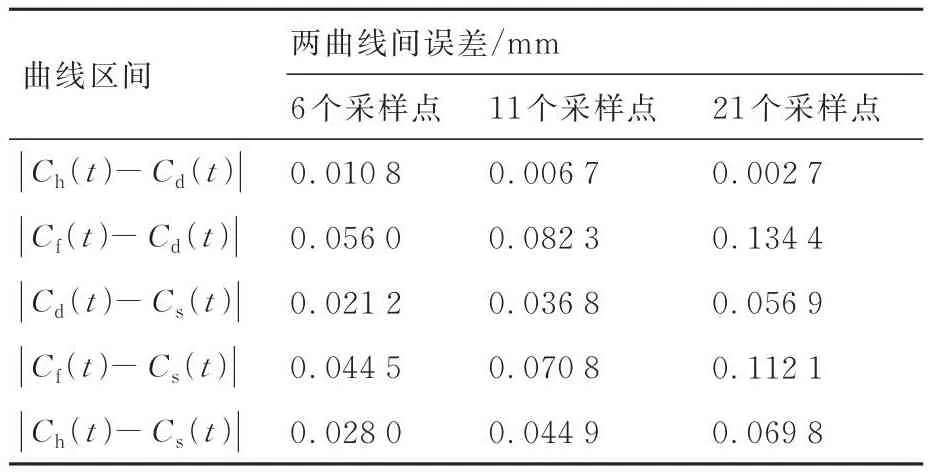
表4 不同采样点个数下各曲线间误差Table 4 Error between each curve with different number of sampling points

3.3 有效性验证与分析

为了进一步验证叶片1案例中计算结果的有效性，在其他叶片与叶片1加工质量一致性好以及测量工艺一致的前提下，将3.1节中得到的21个测量点布置在其他5个叶片上相同位置处，如图10所示。使用在机测量和三坐标测量机检测各个叶片，并基于提出的方法计算5个叶片上在机测量结果拟合误差的上界值，结果见图11。

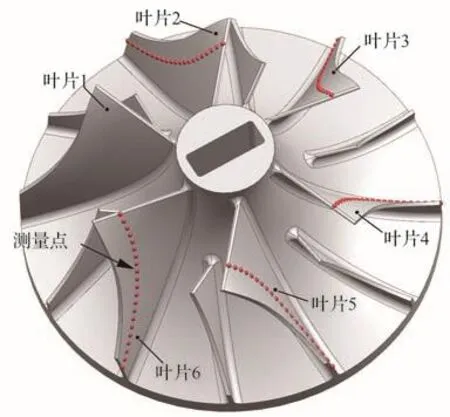
图10 其他叶片上布置的测量点Fig.10 Measuring points planned on other blades

图11 其他叶片上测量点拟合误差的上界值Fig.11 Upper bound of fitting error of measuring points on other blades

分析图11可知：① 叶片6上测量点的拟合误差上界值最大，为0.019 2 mm；叶片2上在机测量拟合误差上界值最小，为0.016 8 mm；5个叶片上测量点的拟合误差上界值均小于给定的拟合允差量0.02 mm；② 由叶片1案例中计算得到的最少测量点数量可用于规划其他5个叶片上采样点。这为叶片类曲面零件在机测量中的测量点规划提供了一种新思路，有助于提高叶片类零件测量工艺的规划效率，实现高效的在机测量。

3.4 其他曲面类零件上应用流程

提出的方法可推广应用于曲轴、模具和齿轮等具有曲面加工特征零件的在机测量采样点规划。通过获取截面轮廓线、规划测量点、拟合测量结果曲线、迭代计算采样步长等关键步骤，确定满足拟合允差时的最少采样点数量。以斜齿轮为例阐述具体应用流程：

步骤1在斜齿轮的齿廓曲面上规划一组截面轮廓线（即齿廓曲线），并在截面轮廓线上基于等步长法采集一系列初始的理论测量点，如图12所示。

图12 齿廓曲面的在机测量应用案例Fig.12 Application case of on-machine measurement of tooth profile surface

步骤2参考齿廓曲面的制造公差合理设定截面轮廓线的在机测量结果拟合允差量。

步骤3使用三坐标测量机和在机测量检测所有测量点，并保存测量结果。

步骤4根据初始步长h=ha在三坐标测量结果和在机测量结果中分别取出对应的检测点坐标，进而拟合理论测量点、在机测量结果和三坐标测量结果获得理论测量点拟合曲线、在机测量点拟合曲线和三坐标测量点拟合曲线。

步骤5根据2.3节和2.4节中方法计算该步长下在机测量结果的拟合误差上界值，并结合式（29）进行拟合允差量的判定。

步骤6若计算出的拟合误差上界值满足拟合允差量的要求，此时该步长对应的测量点数量最少；否则缩短步长h=h/2，重复执行步骤4～步骤6，直至符合设定的拟合允差量要求。

4 结论

1）提出了一种表征截面轮廓线拟合误差的方法，能够从在机测量系统的多源误差中分离并定量表示出在机测量检测结果拟合截面轮廓线的拟合误差。

2）建立了在机测量结果拟合误差上界模型，并提出了在满足给定的拟合允差量前提下、最小化测量点数量的优化方法。该方法适用于其他具有曲面加工特征的零件，并以斜齿轮为例阐述了其具体应用流程，是一种提升在机测量效率的测量工艺优化新思路。

3）以某型号离心式叶轮上叶片的在机测量为例，采用提出的规划方法在满足拟合允差0.02 mm时只需迭代计算3次就可确定最少测量点数量，并在其他5个叶片上进行了有效性验证。试验结果表明本文提出的方法可行、有效，适用于叶片曲面上测量点采样规划，可为大批量叶片在机测量时的采样点工艺规划提供参考。

4）阐述了在机测量中测量点分布对曲线拟合误差的影响规律，在此基础上，融合采样点位置以及由曲线扩展至曲面的在机测量检测点采样策略可作为下一步研究重点。