火箭高温高速喷流注水降噪数值计算与分析

刘俊林，徐希海，张志成，陈小前

1.国防科技大学 空天科学学院，长沙 410073

2.北京特种工程设计研究院，北京 100028

3.北京航空航天大学 航空发动机研究院，北京 100191

运载火箭发射起飞过程中会产生高强度的喷流噪声，能够形成声载荷直接作用在火箭、发射台以及地面操作设备上，产生严重的声振响应，威胁着火箭本体、有效载荷以及仪器设备的服役安全。注水降噪是目前针对火箭喷流噪声最有效的控制方法。20世纪50年代，美国NASA Langley 研究中心就针对飞机喷流噪声问题开展了一系列的注水降噪研究［1］。20世纪60年代以后，冷战背景下航天火箭技术飞速发展，美国、苏联相继开始将注水降温降噪的技术手段应用于降低运载火箭发射喷流噪声，以防护火箭发射设备及设施［2-3］。20世纪90年代中后期，欧洲航天局（ESA）在大型火箭起飞降温降噪方面也开始采用注水降噪技术［4-5］。此外，美国哥达德飞行中心的Alfonsi［6］，美国肯尼迪航天中心的Vu和 Kandula［7-8］，路易斯安那州立大学的Jones等［9］，NASA斯坦尼斯航天中心的Allgood、雅各布斯技术公司的Saunders和洛克希德·马丁公司的Langford［10］均基于缩比火箭发动机模型，针对火箭喷流噪声开展了注水流量、注水速度、注水角度等对降噪效果影响的一系列参数化研究。中国在火箭喷流注水领域的研究方面，对注水降温特性的研究相对较多，南京理工大学的卢晨宇和上海宇航系统工程研究所的施悦等［11］比较了长征七号采用2种不同的水冷却系统对发射台的冷却效果，利用可实现的k-ε湍流模型求解三维Navier-Stokes方程，建立了火箭羽流模型，采用欧拉分散相（EDP）模型对注入冷却水进行模拟，通过与实验对比，分别验证了模型的有效性。北京航天发射技术研究所的陈劲松等［12］基于其实际工程需求对大型火箭发射喷流噪声注水降噪技术进行了较为具体的综述。

火箭喷流噪声的有效控制，很大程度上得益于喷流噪声与注水降噪机理基础理论的研究。喷流噪声是气动声学领域的的经典科学问题。20世纪50年代，Lighthill［13-14］基于其对喷流噪声的研究工作创立了声类比理论，其关于喷流噪声的八次定律，在其后的几十年间都是喷流噪声预测、降噪设计的主要理论公式。20世纪50年代～70年代初，喷流噪声的后续理论大都试图改进或完善声类比理论［15-19］。Lighthill的声类比理论在工程应用上取得了巨大成功，但其本质上是一种“黑箱”，喷流噪声预测的准确与否很大程度上依赖实验或计算获得的声源信息［20-22］。

20世纪80年代中后期，计算气动声学（Computational Aeroacoustics， CAA）的高速发展给喷流噪声的研究提供了新的技术手段，至20世纪90年代中后期更成为气动声学的研究热点［23］。近年来，研究人员采用计算气动声学方法对亚声速和超声速喷流噪声进行了模拟，在准确预测各个噪声分量的基础上，对其发声机理进行了深入研究。李晓东等［24-27］采用计算气动声学高精度数值模拟方法准确捕捉到了超声速喷流啸音的频率与幅值，解释了超声速喷流啸音产生与辐射机理。但由于CAA方法对计算资源的庞大需求，目前尚难以用于火箭超高温高速喷流噪声、尤其是注水降噪多相流下的气动噪声数值模拟及工程预测。

鉴于半经验方法和高精度数值模拟方法在低噪声工程设计应用上的不足。研究者们在计算流体力学方法（CFD）高速发展的基础上建立了基于RANS的喷流噪声预测方法。1978年NASA Glenn实验室的Balsa等以Lilley方程为基础［28］，结合CFD得出的湍流平均信息发展了计算喷流噪声的MGB程序，而后Khavaran［29］又对该方法进行了一系列优化。20世纪70年代，Crow 和 Champagne［30］、Brown 和 Roshko［31］在实验中首次发现了喷流自由剪切层内存在大尺度湍流结构，为Tam（1994［32］，1995［33］）提出的两噪声源模型提供了有力的实验支持。在此基础上，Tam 和 Auriault［34］建立了小尺度湍流喷流噪声预测理论模型，在90°方向预测结果与实验符合得很好，但大尺度湍流结构噪声占主导的下游噪声预测一直难以解决。2009年以来，Obrist［35］、Cavalieri［36］、Reba［37］等研究者从波包理论的角度研究大尺度湍结构噪声的产生机理，并取得了一些成果，Jordan 和 Colonius在2013年给出了比较具体的研究综述［38］。但是目前基于波包理论喷流噪声预测方法的研究也仍然处在初级阶段。2019年徐希海和李晓东［39］在Tam喷流小尺度湍流噪声源模型的基础上，发展了针对喷流大尺度湍流结构噪声的各向异性湍流混合噪声模型，并采用军用与民用飞机的亚声、低超声速喷流噪声的实验数据进行了验证，但目前尚未在火箭超高温、超高声速喷流噪声上得到应用与验证。

本文以某火箭发动机缩比喷管为研究对象，针对火箭发射典型工况，基于计算流体力学及多相流数值计算方法分别开展了孤立火箭喷流与注水降噪条件下的平均流场数值计算研究。分析了注水条件下，水流对火箭喷流平均温度场、压力场、速度场和湍动能场的影响，并在此基础上采用先前发展的基于RANS的喷流噪声预测模型［39］，研究了注水对火箭喷流湍流混合噪声和宽带激波噪声的影响，分析了该预测模型在火箭喷流噪声预测与注水降噪设计方面的实用性，能够为后续实验方案的设计提供基础。

1 喷管模型及数值计算方法

1.1 喷管模型及计算工况

本文以典型拉瓦尔超声速喷管为研究对象，喷管构型如图1所示，喷管入口直径为50 mm，出口直径为67 mm，喷管长度为200 mm。具体的燃气喷流工况及燃气物性参数见表1及表2。

表1 燃气喷管尺寸及喷流工况Table 1 Gas nozzle size and jet flow conditions

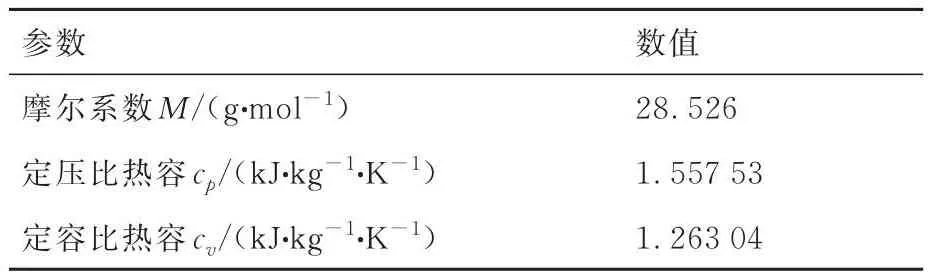
表2 燃气物性参数Table 2 Gas physical parameters

图2给出了注水管尺寸及与燃气喷管相对位置图，注水管中心与燃气喷管出口中心处于同一平面，并向射流方向偏转30°将水注入火箭高温高速射流。注水管出口为长方形，注水管尺寸及注水工况的具体参数见表3。

表3 注水管尺寸及注水工况Table 3 Water injection pipe size and water injection working conditions

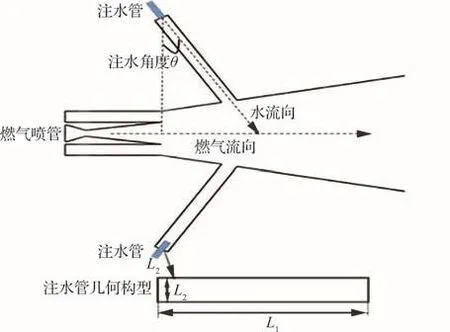
图2 注水管与燃气喷管相对位置Fig.2 Relative position of water injection pipe and gas nozzle

1.2 计算网格设置

计算域的整体网格如图3所示，网格全部采用结构化的六面体网格。如图4喷管附近x-y截面网格细节所示，对喷管固壁边界、喷管出口及喷流自由剪切层处进行加密处理，流向网格最小尺度约为0.000 2De，径向网格最小尺度约为0.000 2De。

图3 计算域和网格Fig.3 Computational domain and mesh

图4 x-y截面网格细节Fig.4 Mesh details on x-y section

1.3 喷流流场数值计算方法

火箭喷流注水流场数值计算软件采用ANSYS FLUENT 商业计算流体力学软件，孤立喷流计算设置为：采用压力基定常求解器，湍流模型为标准k-ɛ湍流模型，空间离散格式为二阶迎风格式，喷管近壁面采用壁面增强处理函数，同时边界层第1层网格为0.000 2De（y+＜1）。

对于火箭射流注水多相流计算问题，涉及燃气、水、水蒸气多相界面的运动、变形、破碎和再融合现象，结构极为复杂。本文选择简化欧拉多相流模型Mixture多相流模型进行数值模拟，Mixture多相流模型假设气液两相在计算单元内充分融合，使用相权重的加权平均方法计算得到混合物的物理参数。在相界面引入滑移速度的概念，允许不同相的流体以不同速度运动，通过求解混合物的连续方程、动量方程、能量方程、次要相的体积分数方程和相对速度的代数方程对多相流进行计算。

在燃气注水工况中，还存在液态水气化问题，高温高速燃气与液态水的两相交界面附近气化现象十分剧烈，会瞬时产生大量的水蒸气，向外扩散，本文中选择Fluent中Lee水蒸发-冷凝模型。火箭喷流注水流场数值计算设置为：采用压力基定常求解器，湍流模型为标准k-ɛ湍流模型，多相流模型为Mixture多相流模型，蒸发系数为1，冷凝系数为1，饱和温度为373.15 K，空间离散格式为二阶迎风格式，喷管近壁面采用壁面增强处理函数，同时边界层第1层网格为0.000 2De（y+＜1）。

1.4 基于RANS的喷流噪声预测方法

本文采用基于RANS的喷流湍流混合噪声预测方法研究火箭喷流噪声及注水降噪技术。图5是基于RANS噪声预测方法的预测流程。首先采用计算流体力学方法获得平均流动信息及湍流信息，而后针对已知的平均流动信息计算喷流内的格林函数，最后结合相应的声源模化函数积分得到远场噪声。

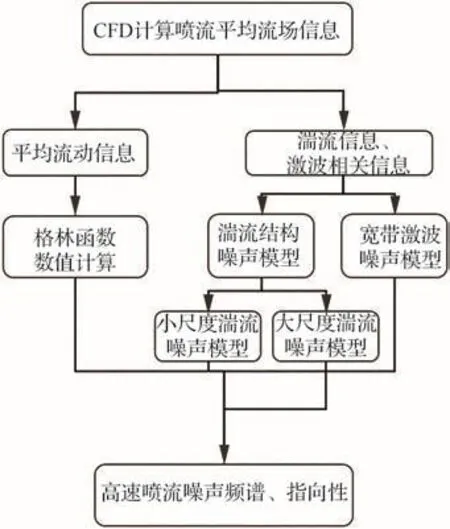
图5 基于RANS喷流噪声预测方法Fig.5 RANS based jet noise prediction method

从图5可以看出，平均流场的准确数值求解，格林函数计算以及气动噪声源模型都是影响喷流噪声预测精度的关键因素。其中平均流场的计算方法已经在1.2节和1.3节说明。喷流噪声格林函数计算方面，本文采用喷流噪声伴随格林函数计算方法，具体计算方法可参见Tam和Auriault［40］、徐希海和李晓东［41］的相关论文，在此处不再赘述。

声源模化方面，对于超声速喷流问题存在湍流混合噪声、宽带激波噪声、啸音3种噪声。本文中只考虑了湍流混合噪声、宽带激波噪声2种宽频噪声源，其中湍流混合噪声又分为小尺度湍流结构噪声与大尺度湍流噪声。喷流小尺度湍流结构噪声本文采用的是Tam和Auriault［34］在1999年发展的喷流噪声小尺度湍流噪声源模型，大尺度湍流结构噪声本文采用的是徐希海和李晓东［39］在2019年发展的喷流噪声各项异性湍流噪声源模型，宽带激波噪声预测本文采用的是NASA Langley 中心Miller［42］发展的宽带激波噪声预测模型。本文采用的喷流噪声预测基于广义声类比方程，具体为

式中：i=1， 2， 3；其余各参数的含义参见文献［39］。

式（1）中广义声类比动量方程及能量方程右边的声源项为

式（1）对应的频域内伴随格林函数方程为

式中：i，j=1， 2， 3；为密度伴随格林函数；分别是动量项相关伴随格林函数；为压力相关伴随格林函数；其余各参数含义参见文献［39］。

在格林函数及声源已知的条件下，喷流远场噪声声功率谱为声源与格林函数乘积的体积分，表达式为

式中：i=1， 2， 3；其余参数定义参见文献［39］。

在平均流场已知的基础上，格林函数G通过对式（3）的数值求解得到。噪声源的模化是基于RANS的喷流噪声预测关键问题，其模化函数的准确性直接关系着预测方法的准确性。

令

式（5）和式（6）中，声源主要分为只与湍流脉动相关的声源项小尺度湍流结构噪声源）以及与平均流动和湍流脉动相干的声源项（大尺度湍流噪声源项）。

本文中对声源模化采用TA方法［34］中的高斯形模化函数，具体为

式中：Afine为小尺度湍流结构声源强度系数；ρ为密度；k为湍动能；͂为喷流流向速度；τ=t1-t2；ξ=x1-x2；η=y1-y2；ζ=z1-z2；τs为小尺度湍流的特征耗散时间，模型中定义为

ls为各方向的特征长度，具体定义为

其中：ɛ为湍流耗散率；cτ、cl-fine分别为时间尺度及空间尺度的经验系数。

大尺度湍流噪声源模化函数为

式中：ls-large、τs、Alarge分别为大尺度湍流噪声源模型中的相干长度尺度、时间尺度及强度系数。其中时间尺度与小尺度湍流噪声源模型中的时间尺度相同，本文中大尺度湍流噪声源的长度尺度定义为

式中：cl-large为长度尺度系数；͂为喷流流向速度；c0为当地声速。其他更为具体的理论及公式细节可参见Tam［34］、徐希海［39］及Miller［42］等的相关论文。

1.5 计算方法验证

由于目前尚没有公开发表的与本文计算工况接近的高温高速燃气喷流及注水工况的流场测试数据，因此本文选择Norum和Brown［43］马赫数Ma=1.2的不完全膨胀喷流实验数据来验证本文定常流动计算方法及相关设置的正确性。验证喷管构型选择NASA ARN2喷管，喷管直径为50.8 mm，总温288 K，喷管出口马赫数为1.2，网格及计算设置与1.2节一致。

图6和图7分别给出了验证算例Ma=1.2不完全膨胀喷流平均速度和静压分布云图（图中r/De为柱坐标下喷流无量纲径向尺寸，x/De为柱坐标下喷流无量纲轴向尺寸），可以明显看见不完全膨胀喷流的激波系结构。图8给出了静压沿着中心轴线分布与Norum和Brown［43］的实验结果及高军辉［44］高精度非定常数值模拟结果的对比。横坐标为以喷管出口直径De无量纲的喷流流向x坐标，纵坐标为以环境压力（Pe=101 325 Pa）无量纲后的静压（P/Pe）。对比结果可以看出，本文数值结果与实验结果相比，前5个激波强度与实验一致性较好，激波位置存在一定偏移，但与高军辉［44］的非定常数值模拟结果一致性较好，且本文第4、第5个激波的数值结果与实验吻合更好。

图6 Ma=1.2不完全膨胀喷流平均速度场Fig.6 Average velocity field of underexpanded jet flow with Ma=1.2

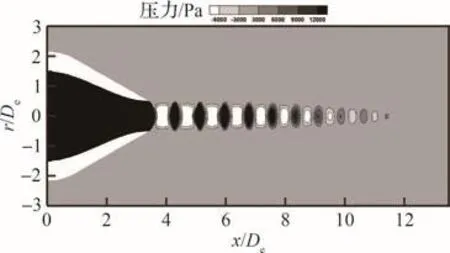
图7 Ma=1.2不完全膨胀喷流压力场Fig.7 Pressure field of underexpanded jet flow with Ma=1.2

图8 喷流中心轴线静压分布与实验结果及高精度非定常数值模拟结果的对比Fig.8 Comparison of pressure distribution on axis line of jet with experimental results and high precision unsteady numerical simulation results

为进一步验证数值计算方法的准确性，本文还针对马赫数3.3、总温3 500 K的热喷流开展了数值验证。并将数值结果与2015年北京理工大学于邵祯博士论文［45］中的高速摄影结果进行了对比。图9为数值计算温度云图与高速摄影结果对比，从图中可以看出仿真计算的燃气喷流流场与实验结果吻合良好，核心区内的温度分布范围、激波结构位置基本一致。

图9 x-y截面温度Fig.9 Temperature on x-y section

在平均流场计算方法准确性得到验证的基础上，本文对基于RANS的喷流噪声预测方法和预测程序进行了准确性验证。图10给出了采用基于RANS的喷流噪声预测方法对Ma=1.47不完全膨胀超声速喷流的预测结果。图中纵坐标SPL为声压级（Sound Pressure Level），横坐标为斯特劳哈尔数（St=fDeUj，Uj为喷管出口速度，f为分析频率）。从Miller［42］的小尺寸缩比模型实验结果中可以明显看出湍流混合噪声、喷流啸音和宽带激波噪声3个分量。本文重点关注超声速喷流宽带激波噪声与湍流混合噪声问题，绿色虚线为宽带激波噪声的预测结果、蓝色点线为湍流混合噪声的预测结果，红色实线为总噪声预测结果。与实验结果对比可以看出，预测方法准确预测了低频段的湍流混合噪声与中高频的宽带激波噪声，平均预测误差在3 dB以下。

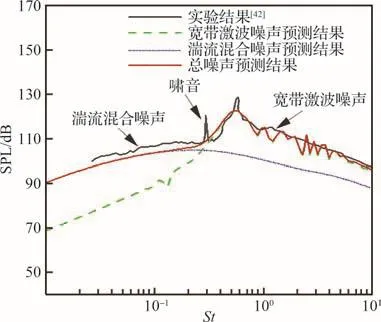
图10 Ma=1.47不完全膨胀喷流噪声预测结果Fig.10 Noise prediction results of underexpanded jet flow with Ma=1.47

2 火箭喷流注水多相流场分析

在计算方法及设置经过校核的基础上，本文依据表1～表3的工况，开展了火箭燃气喷流及注水降温降噪工况CFD数值计算研究。

图11（a）和图11（b）分别给出了孤立喷流与注水降噪条件下500、1 500、3 000 m/s的三维速度等值面分布，同时图11（b）还给出了密度250 kg/m3的等值面。从速度等值面可以直观地看出，在20 m/s的注水工况下，火箭燃气射流的核心区长度明显缩短，500 m/s的等值面流场长度约为孤立喷流的1/2。

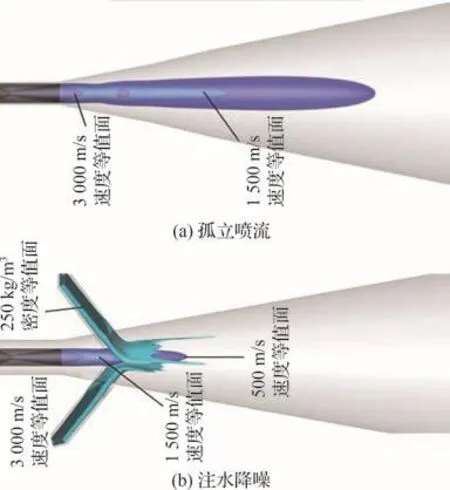
图11 三维速度等值面分布Fig.11 3D velocity isosurface distribution

图12（a）和图12（b）分别给出了孤立喷流与注水降噪条件下z=0截面的静压分布，从孤立喷流的静压分布云图可以看出明显的火箭过膨胀喷流激波系结构，在注水工况下，水流冲击在燃气射流第2个激波结构的位置，冲击下游的激波系在水流的影响下消失。

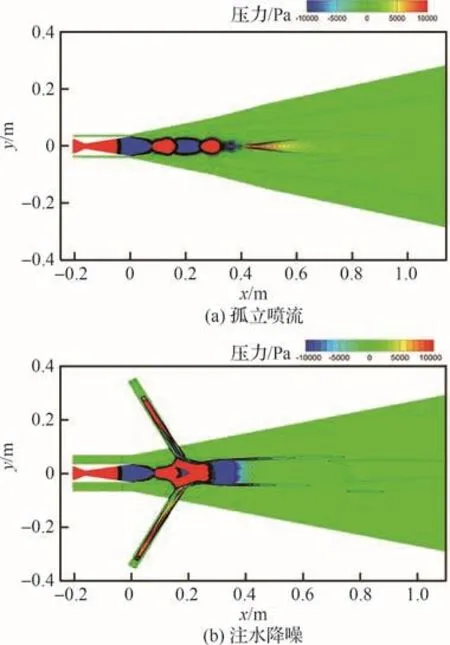
图12 z=0截面的压力云图Fig.12 Pressure contours of section z=0

图13（a）和图13（b）分别给出了孤立喷流与注水降噪条件下z=0截面的速度分布云图，与孤立喷流的速度云图相比，在20 m/s的注水工况下，水流-燃气射流冲击位置之后的水、水蒸气、燃气多相流的速度明显降低。

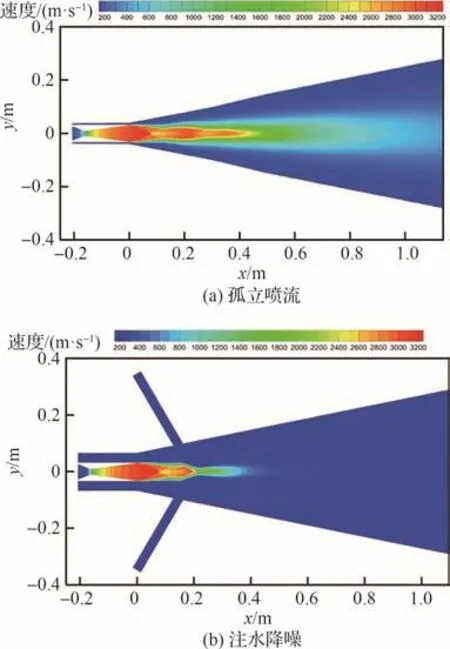
图13 z=0截面的速度云图Fig.13 Velocity contours of section z=0

图14（a）和图14（b）分别给出了孤立喷流与注水降噪条件下z=0截面的湍动能分布云图，与孤立喷流的湍动能云图相比，在20 m/s的注水工况下，水流-燃气射流冲击位置之后的湍动能分布范围变小，但是湍动能峰值明显增强，注水工况峰值强度是孤立喷流的2.5倍。

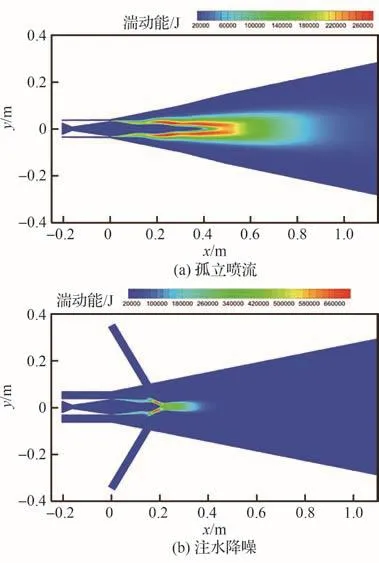
图14 z=0截面的湍动能云图Fig.14 Kinetic energy contours of section z=0

图15给出了高温燃气喷流沿中心轴线的速度分布，横坐标为无量纲喷流流向x坐标（以De无量纲），纵坐标为无量纲流向速度（以喷管出口速度Uj无量纲），可以看出由于过膨胀喷流激波系，孤立燃气喷流前8倍直径的中心轴线速度沿着流向存在大幅度波动，注水工况下，由于水流直接冲击在第2个激波位置，冲击位置后的激波结构在水流的影响下消失，且喷流速度快速降低。

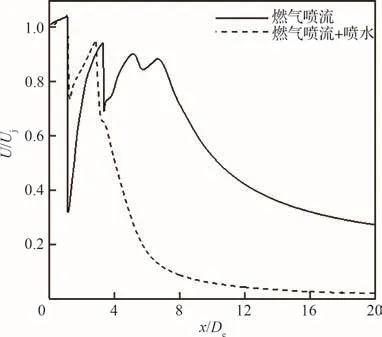
图15 喷流中心轴线速度分布Fig.15 Velocity distribution on axis line of jet

图16给出了高温燃气喷流中心轴线静压分布，横坐标为无量纲喷流流向x坐标（以De无量纲），纵坐标为无量纲静压（以环境压力Pe无量纲），与速度分布类似，由于过膨胀喷流激波系，孤立燃气喷流前8倍直径的中心轴线静压沿着流向存在大幅度波动，注水工况下，由于水流直接冲击，第2个激波后不再存在压力波动，压力趋于环境压力，但值得注意的是第2个激波的强度相对孤立燃气喷流有所增加。

图16 喷流中心轴线静压分布Fig.16 Pressure distribution on axis line of jet

3 火箭喷流注水降噪声学分析

在已经获得火箭高温燃气喷流与注水工况多相流流场的基础上，本文采用基于RANS的喷流湍流混合噪声预测方法研究火箭喷流噪声及注水降噪技术的效果。

3.1 湍流混合噪声

在喷流噪声分析中，斯特劳哈尔数是最重要的表达喷流噪声频率与喷管尺寸和喷流速度相似性的无量纲频率参数。表明了喷流噪声的频率与喷管直径线性负相关，与喷流速度线性正相关的基本特性。由于本文研究的是直径为67 mm的缩比模型，而非全尺寸火箭喷管模型，因此本文对喷流噪声的分析采用St代替频率，众多的研究表明喷流噪声尤其是喷流宽频噪声的能量分布空间主要在St=0.01～10的区间内，因此本文主要分析此频率区间的喷流噪声问题。

图17（a）和图17（b）分别给出了孤立喷流与注水降噪条件下St=2.6时声源分布云图，与孤立喷流的声源分布云图相比，在20 m/s的注水工况下，St=2.6时声源的幅值与分布位置均没有明显区别，这主要是由于火箭喷流高频噪声的声源区位于喷管出口附近，此处水流并未冲击到，因此注水对喷流高频噪声的影响相对较小。

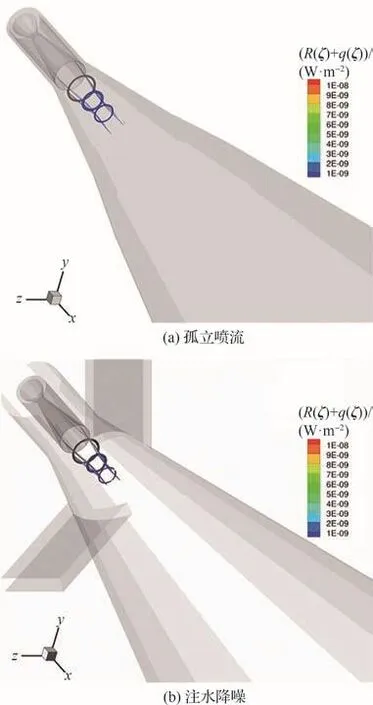
图17 St=2.6 （1 000 kHz）时的噪声源分布Fig.17 Noise source contours when St=2.6（1 000 kHz）

图18（a）和图18（b）分别给出了孤立喷流与注水降噪条件下St=0.026时的声源分布云图，与孤立喷流的声源分布云图相比，在20 m/s的注水工况下，St=0.026时声源的前半部分变化较小，而声源区后半部分分布则区域明显缩小，目前的注水工况，将有效降低以St=0.026为代表的中频噪声。

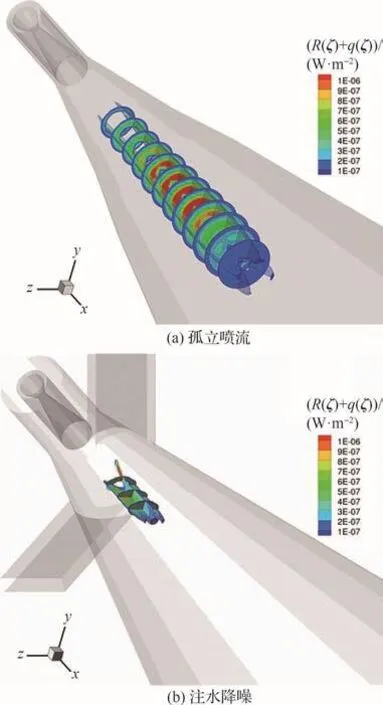
图18 St=0.026 （10 kHz）时的噪声源分布Fig.18 Noise source contours when St=0.026 （10 kHz）

图19给出了上游30°方向、边线90°方向、下游150°方向的燃气喷流湍流混合噪声的预测结果，其中观测点距离喷管出口中心的距离为100倍的喷管出口直径。横坐标为无量纲的斯特劳哈尔数，纵坐标为声压级。整体噪声频谱呈现宽带特征，且指向性明显，下游150°方向的大尺度湍流结构噪声占主导，噪声强度明显高于上游30°和边线90°方向。

图19 燃气喷流湍流混合噪声频谱Fig.19 Noise spectra of gas jet turbulent noise

注水工况下喷流噪声频谱发生明显变化，整体表现为低频噪声降低，高频噪声则有所升高。且各个方向的相对变化并不完全一致。对于喷流上游30°方向，只有在St＜0.01的极低频率下，喷流噪声才略有降低，约2 dB，而St＞0.1的中高频噪声整体提高2～6 dB。

对于喷流边线90°方向，只有在St＜0.06的低频下，注水导致喷流噪声降低，St=0.01时降噪约4 dB，而St＞0.2的中高频噪声整体提高2～4 dB。

对于喷流下游150°方向，注水对喷流湍流混合噪声有明显的降噪效果，在St＜0.3的中低频率整体降噪效果达到6 dB，但高频依然有所升高，约2 dB。

造成上述现象的主要原因是，喷流湍流混合噪声分为大尺度湍流结构噪声和小尺度湍流结构噪声，大尺度结构噪声随着喷流边界层发展逐渐产生、在喷流下游噪声中占主导地位。本文的注水工况下，水流冲击在距离喷管出口中心3倍直径的位置，水流注入后抑制了喷流剪切层大尺度湍流结构的发展，因此导致大尺度湍流结构噪声主导的下游噪声明显降低。但是燃气与水流也会形成一定的冲击效应，这导致了高频噪声的增加。

3.2 宽带激波噪声

对于喷流宽带激波噪声的预测，首先通过傅里叶变换将静压的空间分布转化到波数空间，转换公式为

式中：k1、k2、k3分别对应x、y、z这3个方向的波数。因为本文所涉及的火箭燃气射流的激波结构只在x方向呈现准周期性结构，因此本文只对x方向进行波数变换。

图20（a）所示为孤立喷流波数空间静压分布P(k1，y，z)。横坐标为波数，纵坐标为无量纲径向尺度（以喷管直径De无量纲），可以看出波数k1=50附近存在明显峰值。图20（b）所示为注水降噪喷流波数空间静压分布P(k1，y，z)。可以看出注水后，波数空间静压依然在k1=50附近存在峰值，但其峰值强度相对孤立喷流而言明显降低。

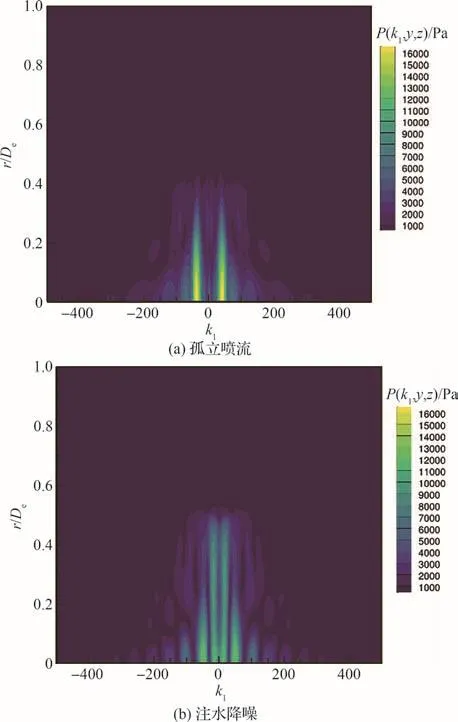
图20 波数空间静压分布P(k1，y，z)Fig.20 Static pressure distribution of P(k1，y，z) in wavenumber domain

图21（a）分别给出了上游30°方向、边线90°方向、下游150°方向的孤立喷流宽带激波噪声的预测结果，其中观测点距离喷管出口中心的距离为100倍的喷管出口直径。图21（a）中横坐标为无量纲的斯特劳哈尔数，纵坐标为声压级。可以看出对于边线90°的观测点，宽带激波噪声的预测频谱在St=0.3的位置存在明显峰值，对于上游30°方向的观测点，峰值频率则偏移到St=0.1附近。下游150°方向的频谱则没有出现类似上游或边线的明显峰值特征，呈现宽频特性。

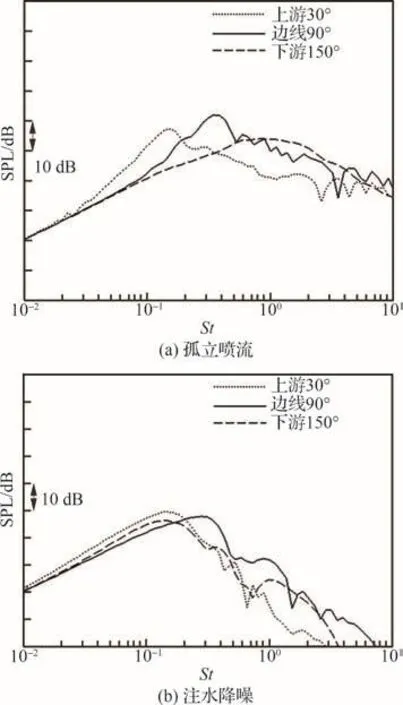
图21 宽带激波噪声的预测结果（上游30°，边线90°，下游150°）Fig.21 Predicted results of broadband shock noise spectra （upstream 30o， side line 90o， downstream 150o）

图21（b）分别给出了上游30°方向、边线90°方向、下游150°方向注水降噪后喷流宽带激波噪声的预测结果对比。相比于孤立喷流，注水喷流的宽带噪声预测结果在各个方向均不存在明显的峰值，这说明注水冲击燃气射流，导致燃气射流的激波系断裂。如图22所示，第2个激波后的激波结构消失有效降低了宽带激波噪声。

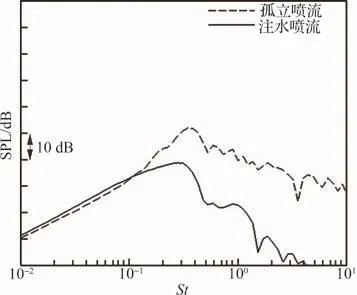
图22 孤立喷流与注水喷流宽带激波噪声对比（边线90o）Fig.22 Comparison of broadband shock noise between jet with and without water injection （side line 90o）

3.3 注水降噪燃气喷流总噪声

燃气射流的宽频噪声由湍流混合噪声与宽带激波噪声组成，图23（a）给出了孤立燃气射流边线上游30°方向喷流噪声，可以看出在喷流上游30°方向湍流混合噪声在低频部分占主导，中高频则是宽带激波噪声占主导。图23（b）则给出了孤立燃气射流边线90°方向喷流噪声，可以看出在喷流边线90°方向湍流混合噪声在低频部分占主导，中高频则是宽带激波噪声占主导。图23（c）给出了孤立燃气射流下游150°方向喷流噪声，可以看出对于下游的观测点，湍流混合噪声在中低频占据绝对的主导地位。

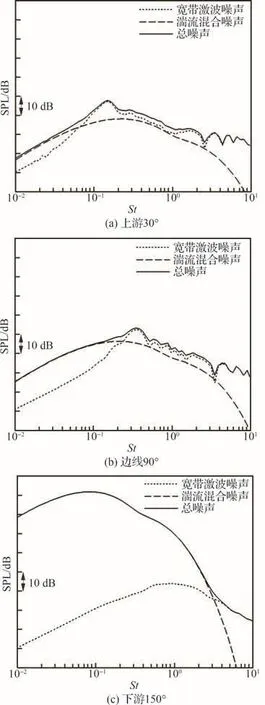
图23 孤立燃气射流在不同观测角度下的喷流噪声Fig.23 Noise spectrum at different viewing angles of gas jet without water injection

图24给出了孤立燃气射流不同观测角度下的噪声频谱对比，可以看出下游150°方向的喷流噪声要明显强于其他方向。趋势上与前人论文中［42］和本文不同工况喷流噪声的实验结果是一致的。

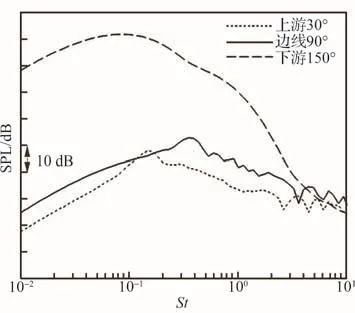
图24 孤立燃气射流总噪声Fig.24 Total noise spectrum of gas jet without water injection

图25（a）和图25（b）分别给出了注水燃气射流边线90°及下游150°方向的总噪声预测结果，可以看出与孤立燃气射流不同，由于注水工况下激波结构被破坏，宽带激波噪声明显降低，导致注水燃气喷流湍流混合噪声在各个方向都占主导地位。

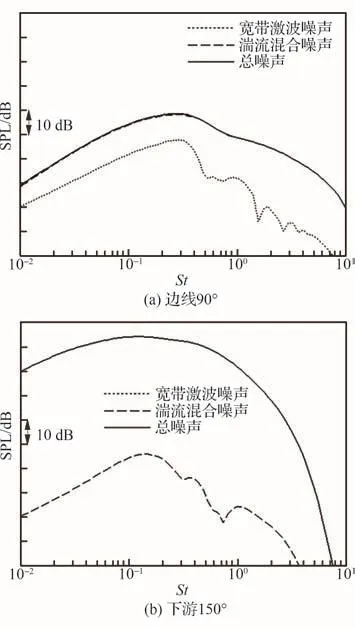
图25 注水燃气射流在不同观测角度下的喷流噪声Fig.25 Noise spectrum at different viewing angles of gas jet with water injection

图26给出了孤立燃气喷流与注水射流频谱在边线90°和下游150°方向总噪声频谱的对比。由于注水破坏了激波结构，同时也抑制了大尺度湍流结构的产生，因此90°方向除了St=0.1～0.2的中频噪声略有升高，其他低频与高频噪声均降低约2～4 dB。下游150°方向由于完全是喷流大尺度湍流结构噪声占主导，因此注水降噪效果最为明显，在St＜0.2的低频段整体降低6 dB。

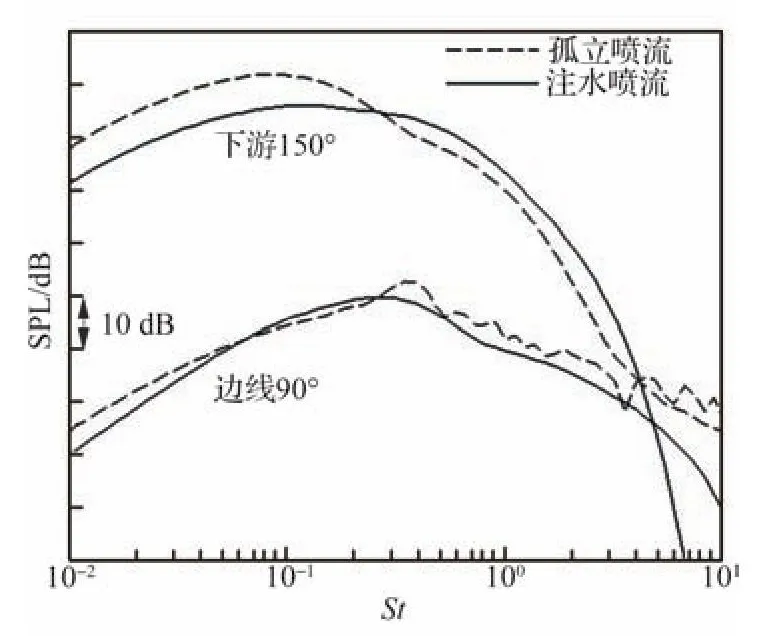
图26 孤立喷流与注水喷流总噪声对比Fig.26 Comparison of total noise between jet with and without water injection

4 结论

本文以某火箭发动机缩比喷管为研究对象，针对火箭发射典型工况，基于计算流体力学（CFD）及多相流模型数值计算方法结合基于RANS的喷流噪声预测模型，研究了火箭高温燃气喷流噪声特性及注水对喷流湍流混合噪声和宽带激波噪声的影响。结论如下：

1） 本文的注水工况下，火箭喷流的核心区明显缩短为孤立喷流的1/2，湍动能分布范围明显缩小，但湍动能幅值显著增大为孤立喷流湍动能的2.5倍。

2） 在本文的注水工况，水流冲击在距离喷管出口中心3倍直径的位置，第2个激波后的激波结构被破坏，大幅降低了宽带激波噪声。

3） 水流注入后抑制了燃气喷流剪切层大尺度湍流结构的发展，因此导致大尺度湍流结构噪声主导的下游噪声明显降低，150°方向St＜0.3的中低频率整体降噪效果达到6 dB。而注水对燃气高频噪声的影响相对较小，部分频段噪声略有升高1～2 dB。

4） 本文基于RANS的喷流噪声预测方法评估了注水对喷流湍流混合噪声和宽带激波噪声的影响，但目前缺乏实验数据验证，后续需要进一步开展相关机理性实验校核验证方法。此外，本文未考虑水蒸气对燃气喷流噪声的吸收效应，需要在未来进一步深入研究。