低烈度区重点设防类建筑的隔震设计与探讨

刘功良，姜伟，马令勇，郭巍，刘桂德

（1.黑龙江八一农垦大学土木水利学院，大庆 163319；2.东北石油大学土木建筑工程学院）

隔震结构是通过设置隔震层，使变形主要集中于刚度相对较小的隔震层[1-2]，从而延长了整体结构的基本周期，并通过上下部结构之间产生较大的相对位移，降低上部结构的地震力，提高建筑物的安全性能[3-5]，保护主体结构及构件在强地震中免遭破坏，确保主体结构在强地震中的安全[6]。根据我国GB 50011—2010《建筑抗震设计规范》规定隔震设计可用于对抗震安全性和使用功能有较高要求，或专门要求的建筑[7]。因此，隔震技术主要用在对使用功能有较高要求或高烈度区的建筑以及投资方愿意通过追加投资来提高抗震安全的建筑物。采用《抗规》给出的水平向减震系数法设计时，将隔震结构分为上部结构、隔震层和下部结构分别设计。这种分离式的设计方法需要使用多个软件，建立若干个不同的计算模型，又常由不同单位分工计算，模型转换和荷载输入等大量繁琐工作也给设计人员带来繁重的工作量，而且计算时间长[8]。所以隔震技术应用并不广泛。根据《建设工程抗震管理条例》第十六条位于高烈度设防地区、地震重点监视防御区的新建学校、幼儿园、医院、养老机构、儿童福利机构、应急指挥中心、应急避难场所、广播电视等建筑应当按照国家有关规定采用隔震减震等技术，保证发生本区域设防地震时能够满足正常使用要求[9]。这就意味着很多低烈度区的重点设防烈建筑也要进行隔震设计，对于没有隔震设计经验的低烈度区的设计师来说是一种挑战。《建筑隔震设计标准》GB T51408-2021 对隔震结构设计提出了不同于《建筑抗震设计规范》GB 50011-2010 的方法，该标准不再采用以前的分部设计方法，而是确立了以“整体分析法”、“CCQC 复振型分解反应谱法”和新一代隔震设计反应谱为代表性内容的方法体系。在抗震设防目标问题上，将原有的“小震不坏、中震可修、大震不倒”提升为“中震不坏、大震可修、巨震不倒”[10]，采用中震进行内力计算和构件设计。采用《建筑隔震设计标准》提出的整体设计法，简化了设计流程，并应用CCQC 复阵型法，结合PKPM-GZ 模块来研究低烈度区建筑物隔震设计的主要流程及探讨在设计过程中存在的问题，探索出的设计方法可为同类工程设计提供借鉴[11]。

1 工程概况

工程为钢筋混凝框架结构，计算模型如图1 所示。建筑功能为某中学食堂，结构共2 层，1～2 层层高均为4.5 m，总高度为9.0 m，平面尺寸为32.2 m×49.5 m，高宽比为0.28。混凝土强度采用了C30 级混凝土，工程抗震设防烈度为7 度，设计基本地震加速度为0.10 g。场地属中软土，场地类别为Ⅲ类，属抗震有利地段，设计地震分组为第一组，场地特征周期为0.45 s。

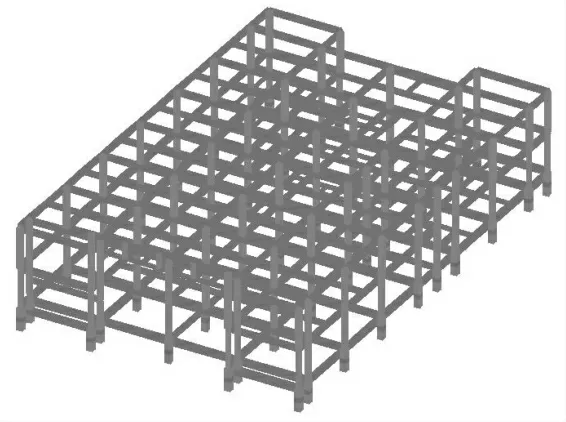
图1 结构计算模型Fig.1 Structure calculation model

2 隔震支座布置

工程采用基础隔震体系，能明显的减轻结构的地震反应，使上部结构处于弹性工作状态，隔震层阻尼大于其他层，消耗地震主要能量[12-16]，隔震层设置在基础和首层之间，工程共使用了45 个隔震支座，其中铅芯橡胶支座L500G4 为25 个，普通橡胶支座N500G 为7 个、N600 为13 个。铅芯橡胶支座见图2，普通橡胶支座见图3[17-19]。隔震支座平面布置见图4，隔震层屈重比为0.023，最大偏心率为2.13%，隔震支座的力学性能参数如表1 所示。

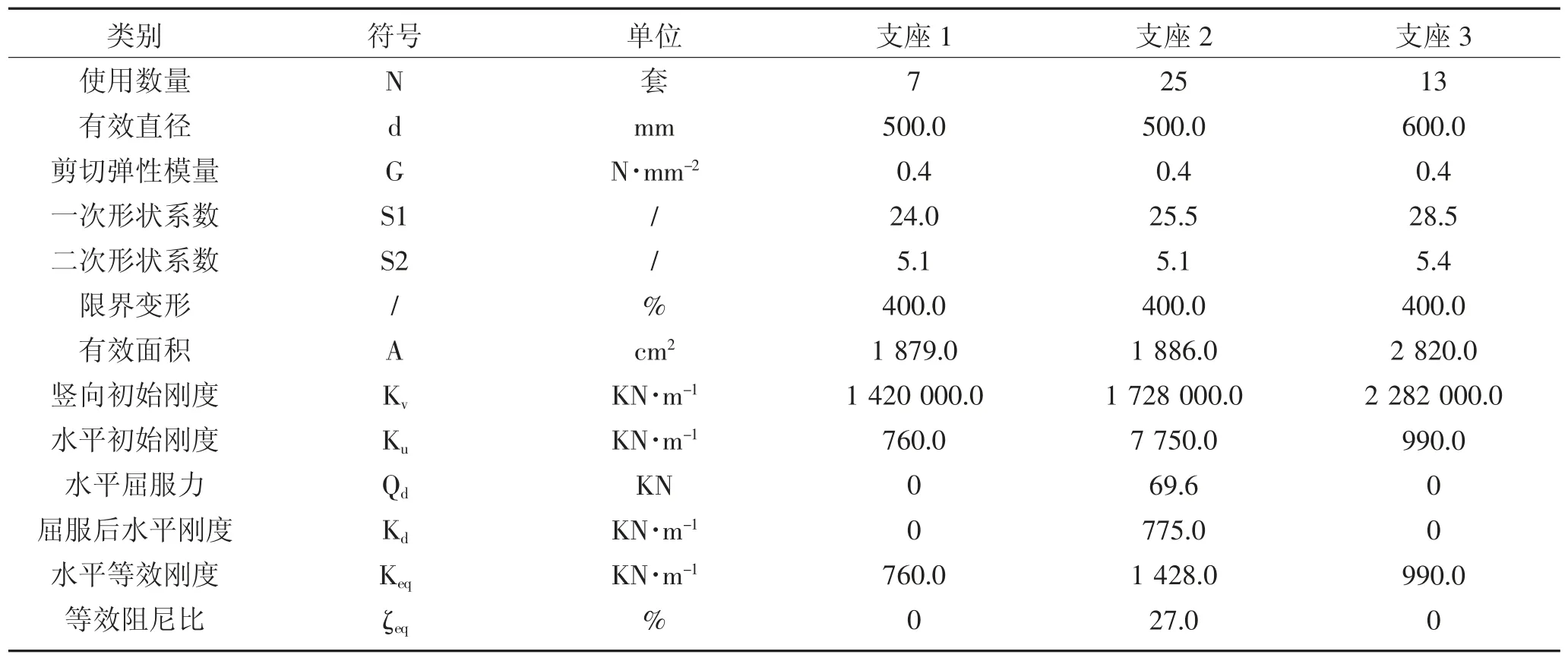
表1 隔震支座使用情况统计Table 1 Statistics of isolation bearing usage

图2 铅芯橡胶支座Fig.2 Lead rubber bearing

图3 普通橡胶支座Fig.3 Common rubber bearing

图4 隔震支座布置图Fig.4 Isolation bearing layout

3 隔震设计

采用《建筑隔震设计标准》中的整体设计法，使用PKPM-GZ 模块建立整体隔震结构模型，即：采用上下部结构、隔震层一体化分析设计，并顺接基础设计的设计分析方法。PKPM-GZ 模块可以根据前处理参数的设定一键生成中震隔震模型、中震非隔震模型及罕遇地震隔震模型，并且可以一并计算。通过在计算结果中切换不同计算模型的菜单来查看相应的计算结果，结构三维模型见图1。

3.1 支墩及隔震支座验算

《建筑隔震设计标准》要求隔震层支墩的设计不仅仅要按照关键构件进行中震弹性正截面及斜截面的承载力设计，同时《隔标》4.7.2 条还要求，隔震层支墩、支柱及相连构件应采用在罕遇地震作用下隔震支座底部的竖向力、水平力及弯矩进行承载力验算，并且要满足大震不屈服，斜截面大震弹性验算[10]，PKPM-GZ 自动生成罕遇地震计算模型，进行支墩构件的包络设计，支墩构件配筋采用设防地震性能设计、罕遇地震抗剪弹性及抗弯不屈服设计的较大值。经计算本工程支墩的截面尺寸为800×800，支墩的配筋结果满足大震不屈服，斜截面大震弹性验算。

《建筑隔震设计标准》要求隔震支座的布置应满足对在重力荷载代表值作用下支座压应力的要求；同时在罕遇地震作用下支座的最大压应力、支座最大拉应力、支座的最大水平位移均不应大于规范的限值。本工程通过计算结果表明，在重力荷载代表值作用下的最大压应力为11.21 Mpa 小于12 Mpa；在罕遇地震下的最大压应力为11.32 Mpa 小于25 Mpa；在罕遇地震下的最大拉应力为0；在罕遇地震下的最大水平位移116.82 mm 小于限值275 mm，以上数值均满足规范要求。

3.2 隔震前后的底层层间剪力比β 确定

工程建筑高度为9 m＜24 m，采用CCQC 复振型反应谱法计算地震作用，对比隔震前后的底层层间剪力比β，来确定隔震结构的抗震措施，层间剪力比β 见表2，隔震层位于2 层；根据2 表格可得，底层层间剪力比β 为0.31 小于0.5，上部结构可按降低一度采取抗震措施，因此，可按六度重点设防采取抗震措施，抗震等级为三级。

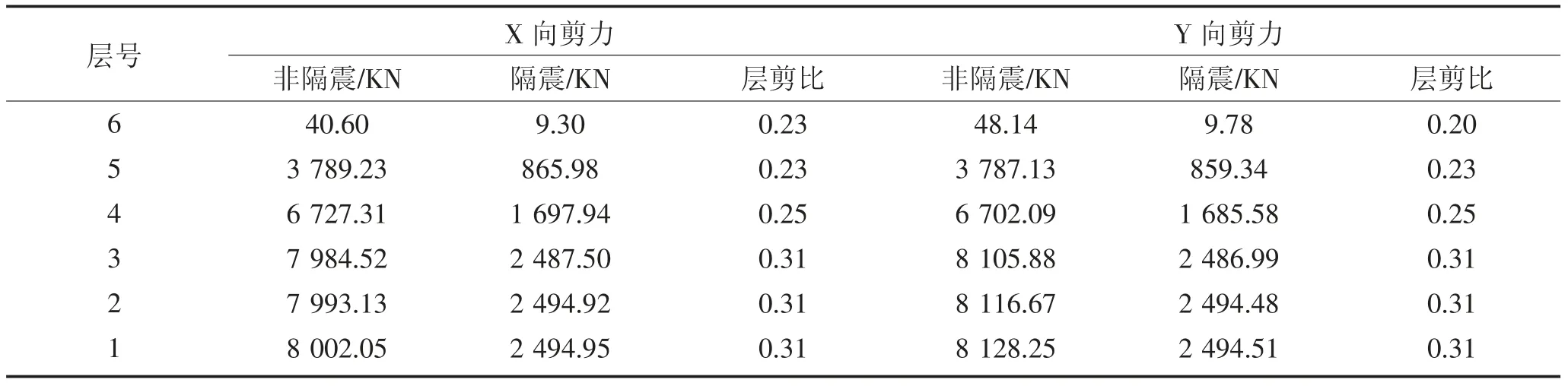
表2 层间剪力比Table 2 Layer shear force ratio

3.3 隔震前后结构自振周期对比

隔震前后结构的基本周期见图5、6，对比隔震前后结构的前三个阵型周期可知，隔震后结构周期明显延长，以第一振型为例，基本周期由隔震前的0.628 6 s 延长至2.233 1 s。周期被拉长，放大3.55倍，有效避开了场地特征周期0.45 s，从而抑制上部结构动力响应，隔绝部分地震能量，减小了地震力，可达到“中震不坏、大震可修、巨震不倒”的要求。

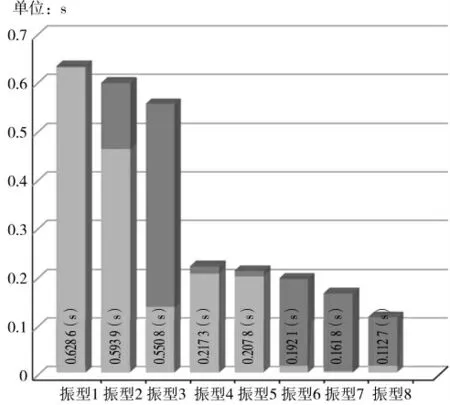
图5 隔震前结构基本周期Fig.5 Basic period of structure before isolation

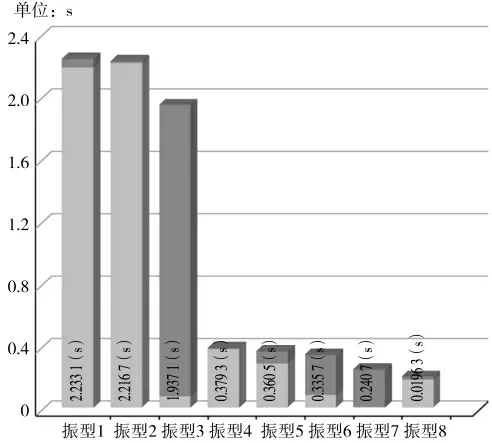
图6 隔震后结构基本周期Fig.6 Basic period of structure after isolation

3.4 隔震层抗风承载力验算

隔震层必须具备足够的屈服前刚度和屈服承载力，以满足风荷载和微振动的要求。《叠层橡胶支座隔震技术规程》[20]规定，抗风装置应按下式进行计算：

工程抗风装置计算结果如下：

X 向顺风向风荷载验算1.4Vwk=1 019.4＜1 738.9 KN（8）满足要求；

Y 向顺风向风荷载验算1.4Vwk=715.6＜1 738.9 KN（9）满足要求。

式中：VRw：抗风装置的水平承载力设计值。当不单独设抗风装置时，取隔震支座的屈服荷载设计值；γw：风荷载分项系数，取1.4；Vwk：风荷载作用下隔震层的水平剪力标准值。根据计算结果可知本工程隔震层具备足够的屈服前刚度和屈服承载力，以满足风荷载和微振动的要求。

3.5 弹性时程分析补充计算

由于项目为多层建筑，且结构形式并不复杂，按照《建筑隔震设计标准》的要求，可以不采用弹性时程分析法进行补充计算，但为了完整的展现低烈度区的隔震设计流程，为其它项目设计提供参考，因此，采用弹性时程分析法进行补充计算，计算结果与CCQC 计算结果包络设计。

3.5.1 地震波的选用

工程选取了实际7 条强震记录，包括5 条天然地震波：T1：TH026TG045；T2：TH035TG045；T3：KOBE，JAPAN；T4：TH113TG045；T5：CHI-CHI，TAIWAN。两条人工波：R1：RH7TG045；R2：RH3TG045。7 条波时程反应谱和规范反应谱曲线及地震影响系数的对比如图7 所示，各条地震波X、Y 方向剪力简图见8、9，其中横坐标为楼层剪力（KN），纵坐标为楼层号。根据地震剪力简图得出X 方向CCQC 计算的底部剪力为2 494.95KN，七条地震波计算的底部剪力平均值为2 700.35 KN，最大值为3 079.46 KN，Y 方向CCQC 计算的底部剪力为2 494.51 KN，七条地震波计算的底部剪力平均值为2 730.76KN，最大值为3 059.40 KN，从以上数据可知时程分析法所计算的底部剪力平均值大于振型分解反应谱法计算值的80%，每条波的计算值大于振型分解反应谱法计算值的65%，且地震波所计算的基底最大剪力不大于CCQC 计算值的135%，所选地震波满足规范要求。结构地震作用效应取时程法计算结果的平均值与振型分解反应谱法计算结果的较大值。取所有地震波楼层剪力的平均值与CCQC 结果进行对比得到各层地震力放大系数见表3，重新进行结构计算，并配筋。

表3 地震力放大系数Table 3 Amplification coefficient of earthquake force

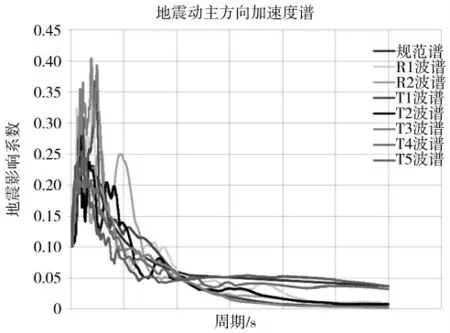
图7 7 条波时程反应谱与规范反应谱曲线对比Fig.7 7 Comparison of time-history response spectrum and standard response spectrum curve

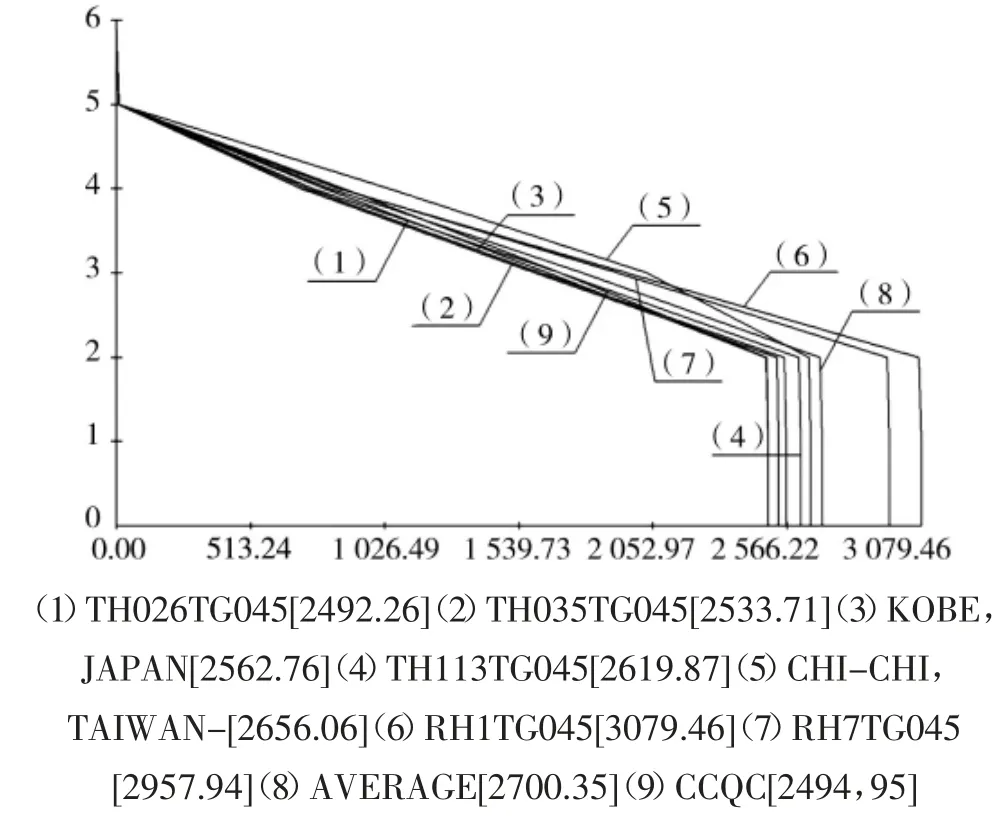
图8 X 方向楼层剪力包络简图Fig.8 X-direction floor shear envelope diagram

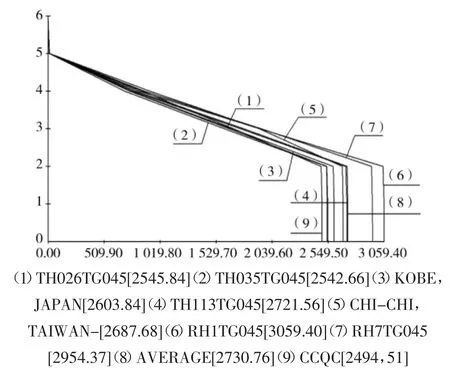
图9 Y 方向楼层剪力包络简图Fig.9 Y-direction floor shear envelope diagram

4 低烈度区隔震结构设计中的问题探讨

隔震设计与传统的抗震设计并不相同，抗震设计需要控制结构的整体指标，例如刚重比、层间位移角、周期比、层间刚度比、剪重比等等，但是隔震结构是否也需要按照抗震设计方法来控制相关指标呢?针对《抗规》与《建筑隔震设计标准》等有关规定，来对现阶段隔震结构设计所存在整体指标控制的问题进行以下探讨：

（1）刚重比：抗震设计时结构刚重比计算是假定荷载是一个倒三角形分布，在这种倒三角形荷载分布下，假定结构底部刚接，来计算结构的倾覆及二阶效应，但是结构隔震设计采用的是设防地震（中震），对于中震下的刚重比的限值是多少，要不要控制以及如何控制《建筑隔震设计规范》并未要求，那设计师要不要控制该指标呢？如果按照从严的标准来说应该控制，刚重比反应结构刚度的大小，如刚度过小，导致结构太柔，导致二阶效应过大。因此，隔震设计时应该按中震下的刚重比来控制，但现有《高规》限值是小震下的限值，这就产生了矛盾，该如何解决需要以后进一步探讨。

（2）层间位移角：因为隔震设计是中震设计，层间位移角按中震下的层间位移角控制。

（3）结构的周期比：从规范的角度来讲周期比主要是避免结构发生过大扭转效应，现行规范中对周期比的控制是针对框架柱底部为刚接的条件下控制的，但隔震结构的扭转效应已经在隔震层上体现了，隔震结构的变形均体现在隔震层上，《建筑隔震设计标准》规定上部结构的重心和隔震层的刚心宜重合，偏心率不超过3%，因此，一般情况下可认为隔震结构周期比不用控制。并且隔震结构的前三个周期均很长，如要控制周期比很难。

（4）结构楼层的刚度比：由于隔震层的存在，隔震层及以下楼层刚度比不需要控制，但是上部结构的刚度比需控制。

（5）结构楼层的位移比及层间位移比：这两个指标是描述结构平面不规则的程度，隔震层以上结构层应该进行控制。但是对于隔震层上一层的层间位移比一般都会超限，因此，对于这一层一般不控制。

（6）结构楼层的剪重比：根据规范要求按多遇地震的地震影响系数的最大值来控制。

（7）结构的抗倾覆控制：传统抗震结构是按照小震验算的抗倾覆，但是隔震结构采用的是大震验算，要求抗倾覆力矩为倾覆力矩的1.1 倍。

（8）轴压比：抗震设计时柱轴压比采用小震的组合计算，墙的轴压比采用的是重力荷载代表值下的轴压比，因此对于墙来说不影响，但对与柱来说是有影响的，因为隔震结构采用的是中震设计的，因此，柱轴压比的计算应采用中震计算。

（9）周期折减：《建筑隔震设计标准》中未提到周期折减，隔震结构不同于抗震结构，在进行振型分解反应谱法计算时，采用实验确定的支座参数计算隔震结构的基本周期不应折减，因为支座的等效刚度已经决定了结构的基本周期，且隔震结构中一般前三个阵型上对结构的有效质量系数的贡献达到99%，基底的剪力基本由前三个振型决定，而后面的振型对剪力的贡献很小，因此可以不考虑周期折减。

（10）隔震层偏心率：《建筑隔震设计标准》明确规定隔震层在两个主轴方向的偏心率不应超过3%。隔震层偏心率大于3%，则说明隔震层的质心与其刚心偏心过大，导致结构角部隔震支座水平位移过大，甚至超过位移限值，而此时结构中部个别隔震支座变形很小，导致结构扭转效应明显，整体隔震不合理，在罕遇地震下扭转变形过大容易引起隔震层支座出现破坏，并导致连续倒塌，因此，应该严格控制隔震层的偏心率。

5 结论

（1）采用《建筑隔震设计标准》中的整体分析法进行隔震设计，该标准确立了以“整体分析法”、“CCQC 复振型分解反应谱法”和新一代隔震设计反应谱为代表性内容的方法体系，方法大大的简化了隔震设计流程。

（2）经计算结构隔震前后的底部剪力比为0.31小于0.5，满足上部结构按本地区设防烈度降低一度的要求采取抗震措施，但竖向地震及相关构造不降低。采用隔震技术后，周期明显被拉长，放大3.55 倍，有效避开地震波中高频部分，削弱隔绝地震作用，从而降低结构响应。

（3）对于低烈度区隔震设计过程中存在的主要问题，提出了解决方法。所得成果可供设计师在低烈度区的重点设防类建筑隔震减震设计工程中参考使用。