基于多策略GWO 算法的不确定环境下异构多无人机任务分配

张安，杨咪，毕文豪，张百川，王雨农

西北工业大学 航空学院，西安 710072

随着军事领域的不断发展，无人机得到了广泛的应用［1-3］，但在执行复杂战场环境下的各类任务时，往往需要多架无人机相互协作完成，以发挥更好的综合作战效能［4-5］。现有的大多数多无人机任务分配问题都建立在任务环境静态且确定的基础上，未考虑如无人机自身性能不稳定，目标执行时长不明确，以及威胁、天气等对任务分配过程中参数的影响，导致预先制定的确定条件下的“最优”任务分配方案往往无法获得预想的结果，甚至无法完成［6-7］。因此，如何在对异构多无人机任务分配时提前考虑不确定性因素对任务分配结果的影响，以提高分配方案的鲁棒性，已成为解决实际战场环境下异构多无人机任务分配问题的关键［7］。

目前考虑不确定因素影响的异构多无人机任务分配研究相对匮乏，通常将不确定条件下的任务分配问题看作为优化问题，并采用随机规划、鲁棒优化和模糊规划等［8］方法进行求解。随机规划作为一种常用的处理不确定性的方法，其引入以概率分布函数描述的不确定性随机变量，并通过建立有关目标函数的随机变量模型，采用不同优化算法进行求解［9］，在求解不确定下的任务分配问题时得到了广泛应用，如文献［10］以两阶段随机规划模型的形式研究了具有随机速度和随机时间窗的异构无人机协同多任务分配问题。但随机规划方法应用的前提是需要估计不确定参数的分布情况，且估计的分布需要与实际分布足够接近，然而在实际战场中不确定事件的发生概率难以获得。因此有学者提出利用鲁棒优化方法求解不确定环境下的多无人机任务分配问题，通过控制决策保守参数，将不确定的优化模型转换为确定的线性规划模型，由于不用假设不确定参数的分布，比随机规划模型更容易求解［11］。文献［12］针对顾客需求不确定下的无人机调度问题，提出了一种两阶段鲁棒优化模型，其求解效果优于随机规划；文献［13］考虑无人机飞行油耗参数等不确定性，利用鲁棒优化方法构建原模型的鲁棒对等形式，实现了任务分配鲁棒性和最优性之间的有效平衡；文献［14］提出了一个鲁棒优化模块以提高时间成本不确定下任务分配方案的鲁棒性。但鲁棒优化方法所求解的任务分配方案存在过度保守的问题，难以权衡系统性能和对不确定性的保护。而模糊规划方法在求解不确定条件下的任务分配问题时，其不确定参数以模糊集的形式描述，仅需根据先验知识选取不确定变量的隶属函数即可，强调的是约束满足的可能性，其求解思路为将模糊规划的目标函数和约束条件转化为一般形式的规划模型，从而求解获得模糊最优解。如文献［15］针对执行时间不确定情况下的资源调度问题，基于模糊规划理论建立了时间-成本约束条件下的模糊资源调度模型，并提出一种改进的混沌蚁群算法对模型进行求解。文献［16］针对带模糊需求与模糊时间窗的车辆路径问题，构建了基于可信性测度理论的多目标模糊机会约束模型，并利用改进的混合遗传算法进行求解。文献［17］提出了一种基于模糊的资源再分配调度模型，将未完成的任务重新分配。文献［18］针对无人机协同对地攻击问题中目标威胁的模糊性，建立一种多阶段的模糊多目标任务分配规划模型，并提出基于多策略融合粒子群算法的纳什均衡求解方法。

本文针对具有不确定任务持续时间、目标的消失时间和无人机航行速度等不确定信息，以及多项复杂约束的异构多无人机任务分配问题，首先基于模糊可信性理论，构建以最小化总成本为优化目标的模糊机会约束规划模型，最后提出一种多策略融合的灰狼优化算法（Multi-Strategy Integrated Grey Wolf Optimization， IMSGWO），引入自适应控制参数调整策略、自适应惯性权重策略、最优学习策略和跳出局部最优策略等，提高算法的搜索能力。本文方法无需提前估计不确定变量的分布律，只需简单估计不确定变量的隶属函数即可。通过对不同测试问题的仿真实验和算法比较验证了IMSGWO 算法的有效性和鲁棒性。

1 不确定环境下的异构多无人机任务分配模型

1.1 问题描述

本文考虑不确定战场空间下，多架异构无人机协同对待摧毁目标执行侦察与打击任务的分配问题，其中任务持续时间、目标的消失时间和无人机的航行速度是不确定的，用三角模糊数表征。战场中不存在禁飞区、地形障碍和突发威胁等，且所有无人机飞行高度相同并具有相同的全局战场信息。要求在满足任务时序约束和时间窗约束的情况下，优化出一个任务分配方案，在上述不确定条件下，使任务的失败率更低，提高任务分配方案的鲁棒性。

1） 异构无人机参数描述

设有3 种类型的无人机（侦察类、打击类和察打一体类）共M架U=[U1，U2，...，UM]，其中侦察类无人机UD只能执行目标侦察任务，打击类无人机UA只能执行目标打击任务，而察打一体类无人机UI可执行侦察和打击任务2 种任务。

用多元组＜Uidi，Utypei，Uvali，ATi，Uposi，vi＞表示无人机i的属性，其所代表的内容分别为无人机i的编号、类型、无人机本身的价值、打击目标的概率、无人机的位置、无人机的巡航速度。用三角模糊数v͂i=[v1i，v2i，v3i]表示无人机i的巡航速度，无人机在执行任务过程中的巡航速度为恒定。本文假设无人机执行侦察任务时不消耗资源，且察打一体类无人机和打击类无人机都携带足够多的打击资源以完成所有目标的打击任务，即本文不考虑资源对任务分配方案的影响。

2） 目标参数描述

设二维不确定战场环境中有N个目标，用T=[T1，T2，...，TN]表示，由于需对每个目标执行侦察任务和打击任务，即战场环境中有2N个任务。

式中：Tjh为目标j的第h类任务（h=1，2），h=1 表示侦察任务，h=2 表示打击任务，每个目标在完成侦察任务之后才能执行打击任务。

1.2 模糊变量处理

与确定的任务环境相比，不确定的任务持续时间、目标的消失时间和无人机的航行速度使任务分配问题中的时间窗约束和时序约束更难以处理。因此，本文基于模糊可信性理论构建模糊机会约束规划模型对上述不确定变量进行处理。

1.2.1 模糊可信性理论

式中：cr∈[0，1]，cr越大表示͂的可能性越大，通过引入偏好值来表征决策者的态度，利用来约束͂的可信度大小。越小，则决策者越倾向于冒着失败的风险去基于͂的条件做决策，相反，越大，表明决策者宁愿重新做出决策，也不愿意基于λ͂≤θ͂的条件做决策。

1.2.2 时间窗约束

设某无人机i完成其待执行的任务序列ai中的前k-1 个任务，则无人机i到达第k个任务位置的时间为

即到达第k个任务的时间为前k-1 个任务的执行时间与无人机从起点依次达到前k个任务位置的旅行时间之和。

当无人机i执行其任务列表中第k个任务时，基于可信性理论，其到达任务k的时间小于任务k的最晚开始时间sk的可信度记为cr1，且cr1∈[0，1]，cr1越大表示无人机Ui到达任务k的时间早于任务k的消失时间的可能性越大，即满足任务k的时间窗约束的可能性越大。

1.2.3 时序约束

对于目标j，设Tj1=ai1L1，Tj2=ai2L2，即其侦察任务Tj1分配给无人机i1任务列表的第L1位置执行，打击任务Tj2由无人机i2任务列表的第L2位置执行，则可得到Tj1的任务完成时间为

则为满足任务的时序约束，基于可信性理论，目标j的侦察任务Tj1的完成时间小于打击任务Tj2的开始时间的可信度为记为cr2，且cr2∈[0，1]，cr2越大表示目标j的侦察任务完成时刻小于打击任务开始时刻的可能性越大，即满足目标j的时序约束的可能性越大。

1.3 收益与代价函数

异构多无人机摧毁目标的代价包括2 个方面：① 无人机执行任务过程中存在的威胁代价C1；② 无人机完成自身任务集的航程代价C2。

设第i架无人机经过目标j后的存活概率为PSi，则PKi=1-PSj，PKj为目标j击毁无人机的概率。因此，单架无人机i执行m个任务产生的威胁代价为

在不考虑路径障碍的假设下，无人机倾向于完成距离自身位置较近的任务，使得相应的飞行油耗较少。航程代价可表述为

式中：Dmax，j为所有无人机相距任务j的最远距离，即

异构多无人机摧毁目标的收益指对目标造成毁伤的价值，定义为目标的价值与毁伤概率，其大小体现了目标的重要程度和无人机的执行能力，能够在决策优化时引导最终分配结果趋向于作战效能最大化。设第i架无人机执行任务j的摧毁概率为Ati，则摧毁目标的收益为

1.4 任务分配模型

异构多无人机在具有不确定任务持续时间、目标消失时间和无人机航行速度等信息的环境下的任务分配问题为多目标模糊机会约束模型，首先通过线性加权和法将问题转化为单目标的模糊机会约束模型，并采用线性尺度变换法将各量纲转化为［0，1］集合内的数值。通过设置不同的权重向量来平衡各个因素对分配结果的影响程度，其中权重ω1、ω2和ω3分别代表攻击目标所产生的威胁代价C1的权重，航程代价C2的权重，以及摧毁目标所获得收益C3的权重，不同的权重取值反映了指挥决策人员的不同决策偏好。由此，基于模糊可信性理论，异构多无人机在上述不确定环境下的任务分配问题的模糊机会约束规划模型为

约束条件为

式（13）表示无人机到达每个任务的时刻早于对应目标消失时间的可信度不小于主观偏好值；式（14）表示每个目标的侦察任务的完成时间早于打击任务的开始时间的可信度不小于主观偏好值，本文设置式（15）确保每个目标的侦察和打击任务都能被执行；式（16）确保每个任务只能被执行1 次；式（17）表示每个无人机的航程约束，Vmaxi为无人机i的最大航程，式（18）表示决策变量xijh的取值。

2 IMSGWO 求解不确定环境下的多无人机任务分配问题

2.1 基本IGWO 算法

灰狼优化算法（Grey Wolf Optimization，GWO）是一种新型群体智能优化算法［19］，模拟了灰狼的社会等级制度和猎食行为，具有实现简单、收敛速度快和全局搜索能力强等优点。为提高基本GWO 算法中的群体多样性、平衡算法的开发和探索能力，并避免过早收敛，文献［20］受启发于狼群中单独狩猎的社会行为，于2021 年提出了改进的灰狼优化算法（Improved Grey Wolf Optimization，IGWO），利用基于维度学习的狩猎（Dimension Learning-based Hunting，DLH）搜索策略，通过选择和更新步骤进一步提高了算法的搜索效率。

IGWO 将狼群中每一个灰狼个体都视为一个潜在解，并通过初始化、移动、选择与更新等3个阶段完成问题的求解：

1） 初始化

N个灰狼被随机分布在给定范围［lj，uj］ 的搜索域中：

第i个灰狼在第t次迭代时的位置表示为：Xi(t)=[Xi1，Xi2，…，XiD]，其中D为问题的维度。整个灰狼群的位置被存在矩阵PopN×D中，每个灰狼Xi(t)的适应度值记为f(Xi(t))。

2） 移动

首先根据适应度值将最好的3 只灰狼依次记为α、β、δ，其余的灰狼记为ω狼，并将灰狼在移动过程中的包围行为建模如下：

式中：A和C为系数，控制参数a在迭代过程中由2 线性递减到0；r1和r2是在［0，1］中的随机向量；MaxIter 为最大迭代次数。

首先计算出狼群内个体与α、β、δ的距离，然后综合判断出个体向猎物移动的方向。

式中：Dα、Dβ、Dδ表示当前候选灰狼与α、β、δ狼之间的距离；Xα、Xβ、Xδ为α、β、δ狼的位置，C1、C2、C3和A1、A2、A3由式（20）得到。

3） 选择与更新

除了灰狼群中的群体狩猎之外，单独狩猎也是另一种重要的行为，因此IGWO 提出基于DLH 的搜索策略。首先为每只灰狼构建一个邻域，并且此邻域中的灰狼之间可以共享信息，通过向邻居灰狼学习，得到另一个候选位置；然后通过比较基本GWO 算法与DLH 搜索策略所求得的新位置候选解的适应度值，选择较优的位置更新为下一迭代过程中的猎物的位置X（t+1）。

首先采用欧氏距离计算灰狼i的当前位置X（it）与Xi～GWO(t+1)之间的距离Ri(t)

然后构建Xi(t)的邻居灰狼群为

并且通过式（26）完成多邻居学习

即DLH 搜索策略所求得的新位置Xi～DLH(t+1)的第d维是通过学习邻居灰狼Xn(t)和狼群中任意灰狼Xr(t)得到的。

在对所有灰狼个体完成DLH搜索后，比较2 个候选对象Xi～GWO(t+1)和Xi～DLH(t+1)，并更新猎物的最新位置：

然后继续迭代移动和选择与更新阶段，直至到达最大迭代次数，算法停止。

2.2 改进策略

对IGWO 算法进行分析可知，通过最优解、优解及次优解确定猎物的位置虽然可使算法具有更明确的指向性，在迭代初期的收敛速度较快，但在优化后期会导致种群多样性降低，优化效果不稳定，易陷入局部最优。同时，算法的控制参数与位置更新策略没有考虑种群的实时变化情况，在一定程度上减缓了算法的收敛速度。

针对上述问题，本文提出了一种多策略融合的灰狼优化（Multi-strategy Integrated Grey Wolf Optimization，IMSGWO）算法，首先采用自适应调整策略来调整算法中的控制参数，提高算法的收敛速度，然后通过学习种群的最优信息来控制算法的搜索方向，同时为了保持种群多样性，采用自适应策略更新最优学习策略中的惯性权重，并改进IGWO 算法中的选择与更新阶段以跳出局部最优。

1） 自适应控制参数调整策略

在IGWO 算法中，控制参数a可调节全局与局部最优搜索的切换。当a较大时搜索步长较大，利于全局搜索，随着迭代次数的增加，控制参数a线性递减，当a较小时搜索步长减小，有利于全局最优值的确定。为进一步提高算法的收敛速度，本文采用自适应调整策略，即综合考虑了当前迭代次数t和当前灰狼个体的适应度值f（it）来确定控制参数ai的大小，

式中：fmin(t)和favg(t)分别为当前灰狼群体的最小适应度值和平均适应度值。式（28）表示，若当前灰狼个体适应度值f（it）小于狼群的平均适应度值favg(t)时，a将由当前迭代次数和当前个体的适应度值大小确定，以提高算法的收敛速度。当fi(t)＞favg(t)时，则控制参数a只由当前迭代次数决定。这一策略既能保证了狼群中每个灰狼根据个体情况确定a，又能保证算法在迭代初期有较好的全局搜索能力，同时具有较好的寻优能力。

2） 最优学习位置更新策略

为使得狼群的下一个位置不比当前的位置差，在搜索的过程中不断趋于更优的位置，提高算法的局部搜索能力和搜索精度，本文提出采用最优学习策略来更新灰狼的位置

式中：Vi(t)为灰狼i的当前速度；ψ(t)为自适应惯性权重；Pibest为灰狼i的最优位置；Pi(t)为灰狼i的当前位置；Xα(t)为当前灰狼群中的最优位置；ξ1、ξ2与ξ3为［0，1］之间的随机数；γ1与γ2为常数，本文中设为γ1=γ2=2。

3） 自适应惯性权重策略

如果算法在迭代收敛过程中灰狼彼此接近，则聚集度会增加，使得灰狼群的多样性降低并陷入局部最优。为提高算法在寻优过程中的多样性，本文引入生物学中表示种群聚集度的指标，采用自适应策略更新惯性权重ψ(t)

式中：k为常数；H（t）为种群聚集度；Fδ(t)为灰狼群适应度的方差。自适应惯性权重ψ（t）主要由式（32）中的聚集度H（t）决定，可通过增加聚集度来弱化灰狼群跟踪局部最优或者全局最优的能力，使得灰狼群在寻优过程中保持多样性。

4） 跳出局部最优策略

IGWO 算法在搜索初期具有较好的收敛速度，全局搜索能力较强，然而随着迭代次数的增多，种群位置变化率降低，因此利用式（33）来帮助种群跳出局部最优：

式中：ε为退火系数，取值为［0.9，1］；T（t+1）为退火温度；ΔF为2 种策略所得解的适应度差值。本文设置即使当DLH 搜索策略所得解的适应度值大于式（23）中原始IGWO 所得解的适应度值时，仍然有一定概率接受DLH 搜索所得的较差解。

2.3 任务序列编码

在IMSGWO 算法中，每个灰狼就是一个备选解，通过种群搜索和位置更新来寻求问题的最优解。为满足在具有不确定任务持续时间、目标消失时间和无人机航行速度的环境下，异构多无人机任务分配问题中侦察任务与打击任务的时序约束、一架无人机同一时刻只能执行一个任务的约束，以及无人机类型与任务类型的匹配约束，本文采用基于实数向量的编码方法，建立灰狼位置与任务分配解的映射关系，其中，灰狼位置的维度与任务的数目相同，并为目标数目的2 倍。灰狼位置的整数部分［X］表示此任务对应的无人机编号，整数部分相同的任务被分配给同一架无人机执行。本文通过限制每个维度上灰狼位置的整数部分的上下界来保证异构多无人机的能力与任务类型匹配，如灰狼位置中对应各目标侦察任务的整数部分取值可为任意可执行侦察任务的无人机编号，打击任务同理。灰狼位置的小数部分｛X｝表示该任务在无人机任务列表中的有限顺序，小数部分越小表示越早执行此任务，如表1 所示。对表中的灰狼位置解码后可得到无人机U1、U2、U3的任务序列分别为：T3，1→T2，1、T3，2→T1，1、T1，2→T2，2。

表1 任务序列编码Table 1 Task sequence coding example

2.4 IMSGWO 求解不确定环境下异构多无人机任务分配问题流程

利用IMSGWO 算法求解具有不确定任务执行时长、目标消失时间和无人机航行速度的环境下的异构多无人机任务分配问题流程如图1 所示，其中虚线框图表示本文改进的内容，并归纳如下步骤：

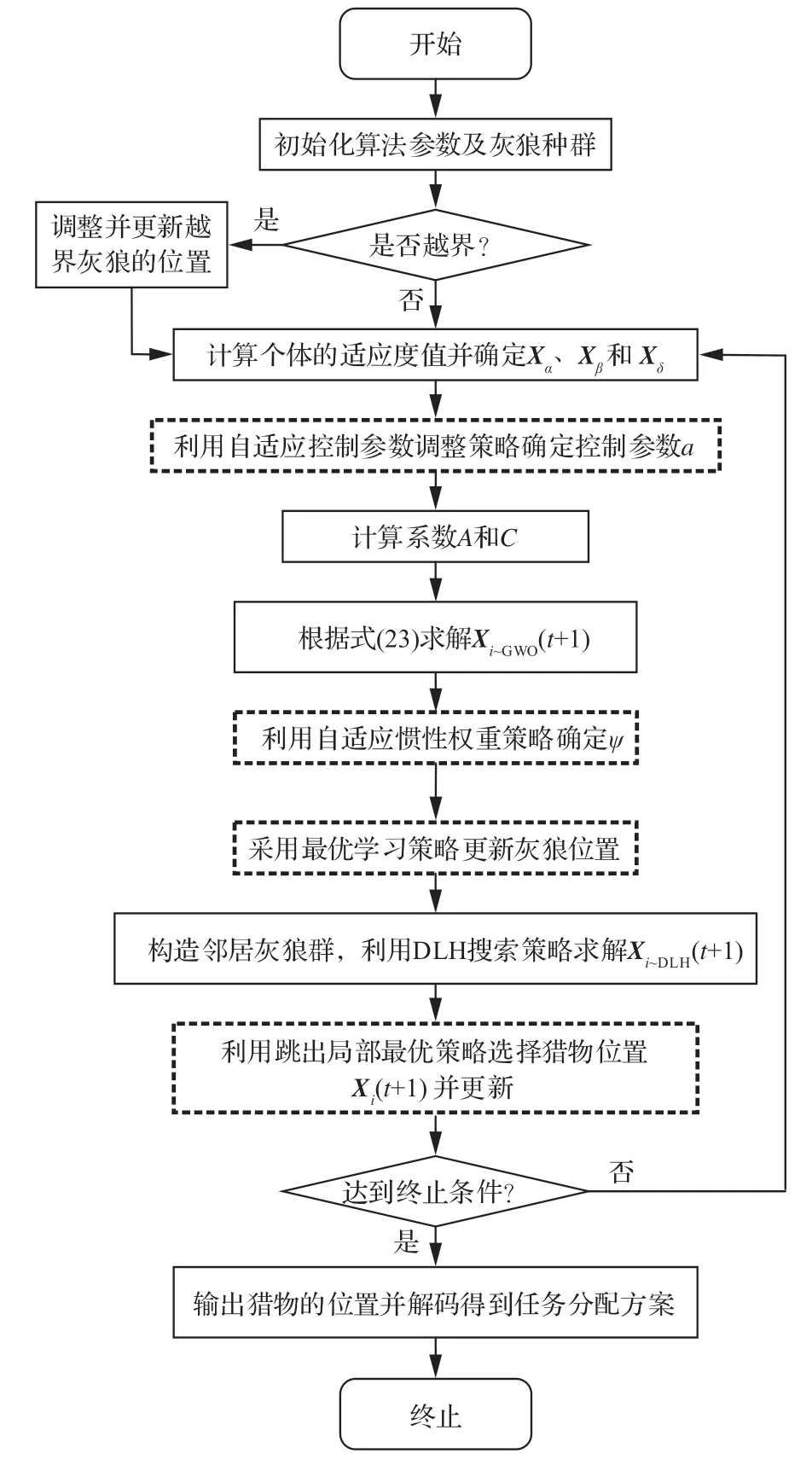
图1 IMSGWO 算法流程图Fig.1 Flow chart of IMSGWO algorithm

步骤1初始化灰狼种群。根据无人机和目标的信息确定灰狼位置的维度及搜索域的上下界［lj，u］j，确定搜索空间的灰狼个数N和最大迭代次数MaxIter，并根据式（19）将N个灰狼随机分布在给定范围的搜索域中，初始化相关控制参数。

步骤2对灰狼种群的位置进行解码，判断是否越界，即是否满足约束条件式（13）～式（18）。若满足，则转步骤3，或不满足，则对越界位置进行调整，更新灰狼位置。

步骤3根据式（12）计算种群中每个灰狼的适应度，确定当前最优解Xα、优解Xβ和次优解Xδ。

步骤4利用式（28）自适应调整控制参数a，式（20）计算系数A和C，并根据式（21）～式（23）计算X（t+1）。

步骤5并通过式（29） ～式（32）确定自适应惯性权重并学习种群的最优搜索方向，得到学习后的解为Xi～GW（Ot+1）。

步骤6根据式（24） ～式（25）构造邻居灰狼群，并通过式（26）构造Xi～DL（Ht+1）.

步骤7根据式（33）选择并更新种群的位置，以跳出局部最优。

步骤8判断算法是否满足终止条件，若满足则输出当前最优位置，并经解码后得到上述不确定环境下最优的异构多无人机任务分配方案，算法结束；否则转步骤2 继续搜索。

3 算法验证及结果分析

3.1 参数设置及实验环境

本文算法参数设置如下：最大迭代次数为MaxIter=500，种群规模Popsize=30。本文所有算法和测试程序均采用MATLAB R2017a 编程实现仿真，操作系统为Windows 10，CPU 为AMD Ryzen 7 PRO，主频为1.70 GHz，内存为16 GB。

3.2 数值实验及分析

实验1为验证IMSGWO 算法求解任务执行时长、目标消失时间和无人机航行速度等不确定信息下异构多无人机任务分配问题的可行性，本文假定4 架无人机在10 km×10 km 的作战区域中对10 个敌方目标执行侦察任务与打击任务，即M=4，N=10，设置决策者偏好值cr=0.8，表2 与表3 分别为无人机与任务的属性表。

表2 无人机属性Table 2 Basic information of UAVs

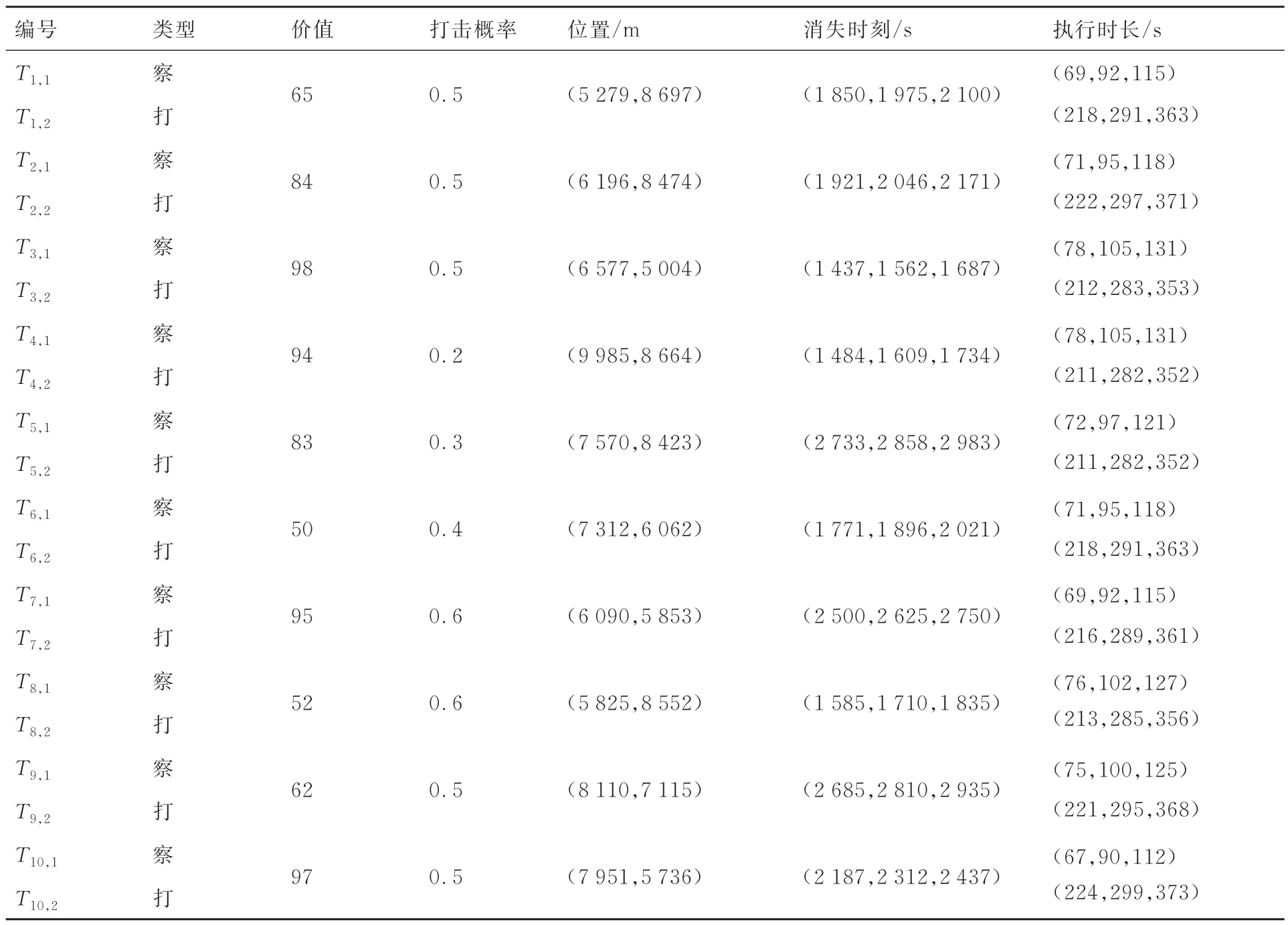
表3 任务属性Table 3 Basic information of tasks

IMSGWO 算法求解过程中适应度变化曲线如图2 所示，可看出由于算法中引入了自适应控制参数调整策略、自适应惯性权重策略与最优学习策略，因此算法的收敛速度较快，在迭代次数t=15 时即可得到可行解。且由于加入了跳出局部最优策略，使IMSGWO 算法能在迭代后期（迭代次数t＞350）能够多次跳出局部最优，具有较好的寻优能力。最终得到无人机分配信息和任务分配信息分别如表4 和表5 所示。

图2 IMSGWO 算法适应度变化曲线Fig.2 Fitness curve of IMSGWO

表4 无人机分配信息Table 4 Schedules information of UAVs

表5 任务分配信息Table 5 Allocation information of tasks

其中表4 中记录了每架无人机执行任务的序列以及行驶距离，表5 记录了执行每个目标的侦察任务与打击任务的无人机编号，以及每个目标满足时间窗约束和时序约束的可信度。可以看出，所有任务都被分配，且都满足上述2 个约束的可信度都可大于给定偏好值cr=0.8 的要求。除此之外，表5 用三角模糊数表示了所有任务的开始执行时刻。因此，此实验验证了IMSGWO 算法在求解具有任务时间窗不确定、任务执行时间不确定和无人机巡航速度不确定等条件下的任务分配问题时的可行性。

实验2为验证无人机数量和目标数量变化对IMSGWO 算法性能的影响，本文分别在目标数量固定（N=10）且无人机数量增加（M=4，6，8），和无人机数量固定（M=4）且目标数量增加（N=8，10，12）的不同任务载荷（任务数量/无人机数量）设置下下测试IMSGWO 算法的求解性能，其求解过程中的平均适应度值变化曲线如图3 和图4 所示。

图4 目标数量增加时IMSGWO 平均适应度变化曲线Fig.4 Average fitness curves of IMSGWO with increasing number of targets

从图3 中可以看出本文所提的IMSGWO 算法在上述所有设置下都可获得可行解，并且随着无人机数量的增加，IMSGWO 算法的适应度值下降减慢，即收敛速度逐渐减慢。由本文所提出的编码方式（表1）可知，当目标数量一定时，无人机数量越多则搜索域越广，导致算法的求解速度变慢。除此之外，图3 显示最终分配方案的适应度值也随着无人机数量不断增加，这是由于当目标数量一定时，无人机执行任务所获得的总收益相差不大，但航程代价与威胁代价却随着无人机数量增加而不断增加，导致最终任务分配方案的适应度值不断增加。

从图4 中可看出当无人机数量一定时，IMSGWO 算法的收敛速度随目标数目的增加逐渐减慢，这是由于目标数量的增加导致灰狼位置编码的维度也线性增加，因此在求解同时满足所有目标的时序约束和时间窗约束时求解难度增大，使得算法需要更多的迭代循环寻找可行解。除此之外，随着目标数量的不断增加，平均每架无人机所需要执行的任务数量增加，使得无人机的任务列表完成时间和航程代价都随之增加，因此本文所提算法所求得的最终适应度值也随着目标数量而不断增加。

实验3为验证所提算法的优越性，本文考虑3 组任务载荷递增的设置：M=6、N=8，M=4、N=10 和M=4、N=12，并将IMSGWO 与3 种经典单目标优化算法PSO、GWO、IGWO，以及一种多目标优化算法MOPSO 在3 种任务载荷设置下独立运行10 次。其中PSO 算法的惯性权重为w=0.9，学习因子c1=c2=2，最大速度Vmax=3；MOPSO 的惯性权重w=0.9，学习因子c1=c2=2，存档规模Archive_Size=30，每个维度的网格数grid_size=10，约束因子α=0.1， 最大速度Vmax=3，突变因子μ=0.1。MOPSO 作为经典的多目标优化算法，为便于与其他单目标优化算法进行比较，本文利用式（12）来评价粒子的性能，即用相同的权重ω1，ω2和ω3来计算每个粒子的适应度值。若MOPSO 不能寻得最优解，则选择种群中适应度值最小的粒子作为最终解，若有可行解存在存档Archive 中，则统计Archive 中所有可行解的平均适应度值作为当前随机运行的最终适应度值，并选择Archive 中适应度值最小的粒子作为最终的任务分配方案。最终任务分配结果的平均值统计记录在表6 中，最优结果用粗体表示，其中BST、AVG、WST、STD 与AVGIter 分别表示算法随机运行10 次所得任务分配方案结果的适应度的最优值、平均值、最差值、标准差和首次得到可行解的迭代次数，AVGDis 和AVGComTime 分别为10 次任务分配方案中所有无人机行驶距离的平均值和任务列表完成时间的平均值，由于每个无人机的任务列表完成时间表示为三角模糊数，因此利用最可能的估计值来计算所有无人机任务列表完成时间的平均值。

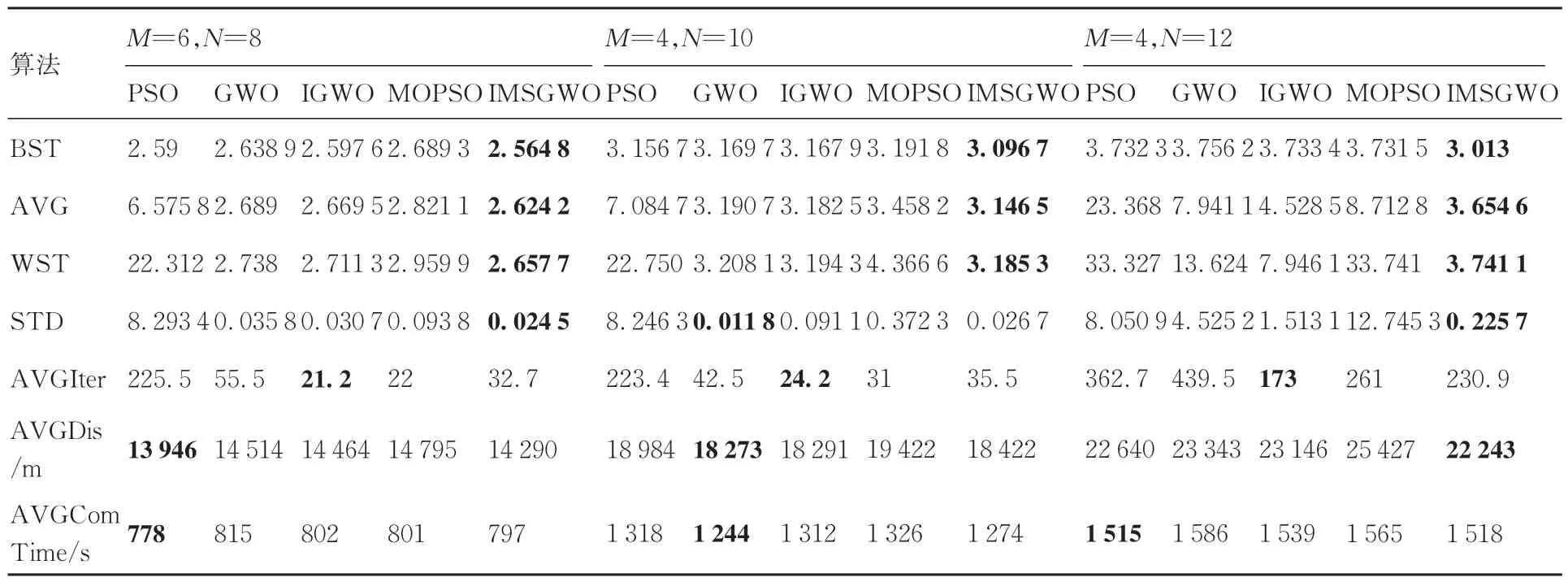
表6 5 种算法在3 种不同设置下的性能比较Table 6 Comparison of performance of five algorithms with three different settings

由表6 可知，本文所提的算法在3 种不同任务载荷设置下的最优适应度值BST，平均适应度值AVG 和最差适应度值WST 都优于其他四种算法，证明了本文所提IMSGWO 算法具有更好的寻优能力。由WST 值可知PSO 算法在3 种任务载荷设置下都存在无法找到可行解的情况（即适应度值＞10），并且GWO 算法和MOPSO 算法在较高的任务负载情况（M=4，N=12）下也存在无法找到可行解的情况，但IMSGWO 算法和IGWO 算法在所有情况下均能寻得可行解，且只在M=4，N=10 的设置下，IMSGWO 算法适应度值标准差STD（0.026 7）略高于GWO 算法（0.011 8），而在其他2 种设置下其STD 都为最优，证明所提算法具有较好的稳定性。由于PSO、GWO 和MOPSO 存在不能求得可行解的情况，因此只统计能够求得可行解时的首次获得可行解的迭代次数AVGIter，可看出，尽管IMSGWO 算法在3 种情况下的AVGIter 都略大于IGWO，但仍小于其他3 种算法，证明所提算法有较快的收敛速度。除此之外，IMSGWO 算法在3 种不同任务载荷设置下所得任务分配方案的无人机平均总行驶距离AVGDis 和平均任务列表完成时间AVGCom-Time 都与最优值相差不足2.5%，表示5 种算法求得任务分配方案的平均时间代价和航程代价接近。同时可注意到，随着任务载荷的增加，每架无人机平均需要完成任务的数量增加，无人机行驶的航程距离和无人机完成任务列表的时间都不断增加。

5 种算法在3 种不同任务载荷设置下求解过程中的平均适应度值变化曲线如图5 所示。从图中可以看出，由于PSO 算法在迭代过程中易陷入局部最优，存在无法成功求得可行解的情况，因此其平均适应度值远高于其他4 种算法。由于MOPSO 获得可行解并存储在Archive 中，当存在其他可行解支配Archive 中任一可行解时，则算法的平均适应度值更新一次，因此如图5 所示，MOPSO 算法在迭代前期平均适应度值的变化次数多于其他4 种算法。除此之外，由于惯性权重的设置不同，MOPSO 算法寻得的非支配解并不一定是式（12）评价下的更优解，因此MOPSO 算法在迭代过程中其平均适应度值并不总是下降。在前2 种任务载荷设置下MOPSO 算法的求解速度较快，但在迭代后期容易陷入局部最优，导致最终适应度值高于GWO、IGWO 和IMSGWO算法，并且在M=4、N=12 的载荷设置下存在无法求得可行解的情况。除此之外，GWO 算法在3种任务载荷设置中不仅收敛速度较慢，且最终适应度值也较高，算法求解能力不强。IGWO 算法由于在GWO 算法的基础上添加了DLH 搜索策略，与PSO 算法和GWO 算法相比不仅收敛速度较快，最终适应度值也低，具有较好的求解能力；而本文提出的IMSGWO 算法在IGWO 算法的基础上进一步添加了自适应控制参数调整策略、自适应惯性权重策略、最优学习策略和跳出局部最优策略，使得算法不仅在前期的收敛速度与IGWO 算法接近，且其最终平均适应度值远低于其他4 种算法，并且能够在迭代后期（t＞450）多次跳出局部最优，具有较好的寻优能力。充分证明了本文所提出的融合多种改进策略的IMSGWO 算法与其他4 种算法相比，在求解具有不确定任务执行时长、不确定目标消失时间和不确定无人机航行速度等信息的异构多无人机任务分配问题时具有更好的性能。除此之外，根据表1 所提出的编码方式，随着任务载荷的增加，算法的求解难度也不断增加，导致5 种算法都需要通过更多次的迭代来进一步寻求更优的分配结果。

图5 3种任务载荷设置下5种算法平均适应度值变化曲线Fig.5 Average fitness curves of five algorithms with three different settings

实验4为验证决策者偏好值对不确定任务执行时长、不确定目标消失时间和不确定无人机航行速度等信息下的异构多无人机任务分配方案效果的影响，图6 统计了决策者偏好值cr按幅度0.1递增时IMSGWO 算法在3 种不同任务载荷设置下随机运行10 次的分配方案的适应度值和平均任务完成时间。除此之外，由于本文中不确定信息=(λ1，λ2，λ3)的上下界λ1和λ3由λ2和不确定程度χ确定，即λ1=(1-χ)λ2，λ3=(1+χ)λ2，为验证不确定信息的不确定程度对任务分配方案性能的影响，图7统计了不确定程度为低中高，即χ分别为0.1、0.3、0.5 时，IMSGWO 算法随机运行10 次的任务分配方案的适应度值和平均任务完成时间。

图6 3 种不同设置下偏好值cr递增时的平均任务完成时间与平均适应度值信息Fig.6 Average task completion time and average fitness with increasing preference value cr and three different settings

图7 3 种不同设置下不确定程度χ 递增时的平均任务完成时间与平均适应度值信息Fig.7 Average task completion time and average fitness with increasing uncertain degree χ and average three different settings

由图6 可知，随着偏好值cr逐步增加，3 种任务载荷设置下的平均无人机任务列表完成时间AVGComTime 即时间代价不断增加，导致分配方案的适应度值总体逐步增加。这是因为当cr递增时，决策者逐渐偏向于保守型，为尽可能减少目标时序约束被违反的可能，目标打击任务的开始执行时刻会推迟，导致无人机的平均任务完成时间不断增加，所得任务分配方案的适应度值也随之增加。如图7 所示，由于不确定程度χ的增加，为保证满足所有目标的时序约束，任务的开始时刻被推后，致使无人机的平均任务完成时间增加，任务分配方案的适应度值也随之增加。

实验5在本文的研究中，任务持续时间、目标消失时间和无人机的航行速度等都为不确定信息，为验证IMSGWO 算法所求解的任务分配方案在任务实际执行过程中的性能，首先利用随机模拟算法［21］（Stochastic Simulation Algorithm， SSA）模拟上述不确定信息的实际值，然后为了以最小改动实现动态调整，本文利用分布式的性能影响算法（Performance Impact， PI）［22］中的任务包含阶段，在不影响原有任务分配方案执行顺序的前提下完成对失败任务的重分配。具体地，PI 算法利用任务包含阶段将失败的任务循环插入类型相符的无人机任务列表中剩余任务间的所有位置，判断插入位置是否满足时序约束和时间窗约束，并利用无人机删除失败任务对任务分配方案整体的影响与不同无人机在不同位置添加任务的影响之间的差值，来衡量此任务重分配方案的性能，具体算法可参考文献［22］。

为了不失一般性，在3 种的任务载荷设置下，统计3 种决策者偏好cr设置下和3 种不确定程度χ设置下的IMSGWO 算法所求任务分配方案的动态性能，如表7 与表8 所示。首先在每种设置下随机生成20 种不同的目标和无人机信息，并在IMSGWO 算法求得满足约束的可行解后，为每个可行解利用SSA 算法随机生成20 组不确定信息的实际值，并统计此实际情况下，原任务分配方案需要重分配的比例RePer，以及成功重分配的比例ReSucPer。

表7 IMSGWO 算法在不同任务载荷和决策者偏好下所求任务分配方案的动态性能Table 7 Dynamic performance of IMSGWO with different settings and preference value

表8 IMSGWO 算法在不同任务载荷和不确定程度下所求任务分配方案的动态性能Table 8 Dynamic performance of IMSGWO with different settings and uncertain degrees

由表7 和表8 可知，当决策者偏好cr或者不确定程度χ一定时，随着任务载荷的增加，IMSGWO 所求得的任务分配方案中有更多任务在实际执行过程中无法满足约束，需要执行更多次的重分配以保证目标的成功完成，并且由于任务载荷增加使得每架无人机完成其任务列表的时间更长，导致添加失败任务之后任务列表中其他任务的时序约束和时间窗约束无法满足的可能性更大，从而使成功重分配的比例随任务载荷的增加而降低。

除此之外，表7 的结果表明，当任务载荷一定时，决策者主观偏好值cr的增加意味着决策者倾向于更保守的任务分配方案，即IMSGWO 所求得的任务分配方案能够更大程度地规避不确定任务持续时间、目标消失时间和无人机航行速度带来的影响，所有任务成功执行的概率更高，因此需要动态调整的任务分配方案的比例不断降低。同时，当任务载荷一定时，决策者偏好增加会使IMSGWO 求得的任务分配方案有更多冗余时间，因此更容易处理失败任务，重分配成功的比例随偏好值的增加而增加。

如表8 所示，当不确定程度增加时，更多已分配的任务在实际执行过程中无法满足时序约束和时间窗约束，因此在任务载荷一定时，需要重分配的比例随不确定程度的增加而增加。同时，不确定程度的提高意味着无人机更容易利用冗余时间处理失败任务，因此重分配成功的比例随偏好值的增加而增加。

4 结 论

本文针对具有不确定任务执行时长、不确定目标消失时间和不确定无人机航行速度等不确定信息以及复杂约束的异构多无人机任务分配问题，首先将不确定信息作为模糊变量处理，并基于模糊可信性理论，首次构建以最小化总成本为优化目标的异构多无人机任务分配问题的模糊机会约束规划模型，并设计了一种多策略融合的灰狼优化算法（IMSGWO）进行求解。实验结果表明，所提算法可求解不确定环境下的异构多无人机任务分配问题，使分配方案对任务执行过程中的不确定性因素具有较好的抗干扰能力。未来将针对现实中存在的不确定任务资源需求、不确定任务位置等进行研究，并进一步改进求解算法。