高功率脉冲对接地传输线耦合的FDTD方法

王一凡，田 炜*，王云康

（1.延安大学 物理与电子信息学院，陕西 延安 716000；2.榆林市生态环境局 固体废物管理中心，陕西 榆林 719000）

随着高功率电磁脉冲源在实际生活中日益广泛地使用，电子设备面临的电磁环境越来越复杂，电磁脉冲将会通过散热孔、连接电缆、外部天线等对设备内的电子元件产生电磁干扰［1-5］。即使对电子设备进行了电磁兼容设计，但若用于连接电子设备的传输线并没有防护措施，特别是直接暴露在外的传输线受到电磁脉冲照射时，就会在线路上产生电磁耦合，电磁能量将通过传输线进入设备内部进行电磁攻击，进而损毁设备的敏感电子元件［6-9］。因此，开展电磁脉冲对传输线的瞬态耦合问题研究对于线路和设备的防护具有重要意义。

近年来，有关电磁波对传输线的耦合研究取得了一系列进展。AGERWAL等［10］采用时域有限差分（FDTD）法研究了不考虑背景的多导体传输线电磁耦合问题，并给出了计算中的稳定性条件；ERDIN等［11］采用SPICE等值电路法研究了电磁脉冲激励多导体传输线的电磁耦合问题；SHINH 等［12］提出了一种快速的闭合SPICE 模型，计算了接地多导体传输线的瞬态电磁耦合，分析中忽略了背景的电磁贡献。考虑接地背景反射的电磁耦合研究，近年来也取得了一系列进展，DIENDORFER［13］采用传递电流模型给出了雷达脉冲激励场，根据镜向原理解决了接地平面的电磁贡献，并运用有限差分方案研究了传输线终端负载的电磁耦合问题；REN 等［14］运用FDTD方法研究了雷电脉冲对接地传输线的电磁耦合问题，其中，背景反射场采用电磁场FDTD 来计算，而电磁耦合通过传输线FDTD 来分析。本文针对接地传输线问题，采用了一种频域反射与傅里叶变换相结合的方案来分析地面背景的电磁反射，再运用FDTD 方法计算了高功率电磁（HPEM）脉冲激励多导体传输线的电磁耦合，数值计算得到了多导体传输线接地负载上的时域感应电压，并分析了直接照射波参数、负载参数对电磁耦合的影响规律。

1 基本原理

1.1 入射波的引入

入射波激励下的多导体传输线模型如图1 所示，近地平面上的双导体传输线沿着z轴放置，长度为L，传输线终端的接地电阻分别为RS1、RL1、RS2、RL2。

图1 入射波激励下的多导体传输线几何示意

由于所研究的导体传输线长度很短，且传输线本身损耗极小，可将其视为无耗导体传输线。空间电磁场对双导体传输线的电磁耦合可以通过传输线方程来描述。在入射场激励下，多导体无耗传输线电报方程［15］可表示为

其中，电压V(z，t)和I(z，t)分别为电压矩阵和电流矩阵，L和C分别是单位长传输线的分布电感矩阵和电容矩阵，ET和EL分别是外场激励分布的电压源和电流源。

入射波矢量指向直角坐标系的坐标原点，它与x轴的夹角为θP，在yOz平面上的投影与y轴的夹角为φP，如图2A 所示。入射波的极化采用a→θ和a→φ为单位矢量的局部坐标来显示，具体见图2B。

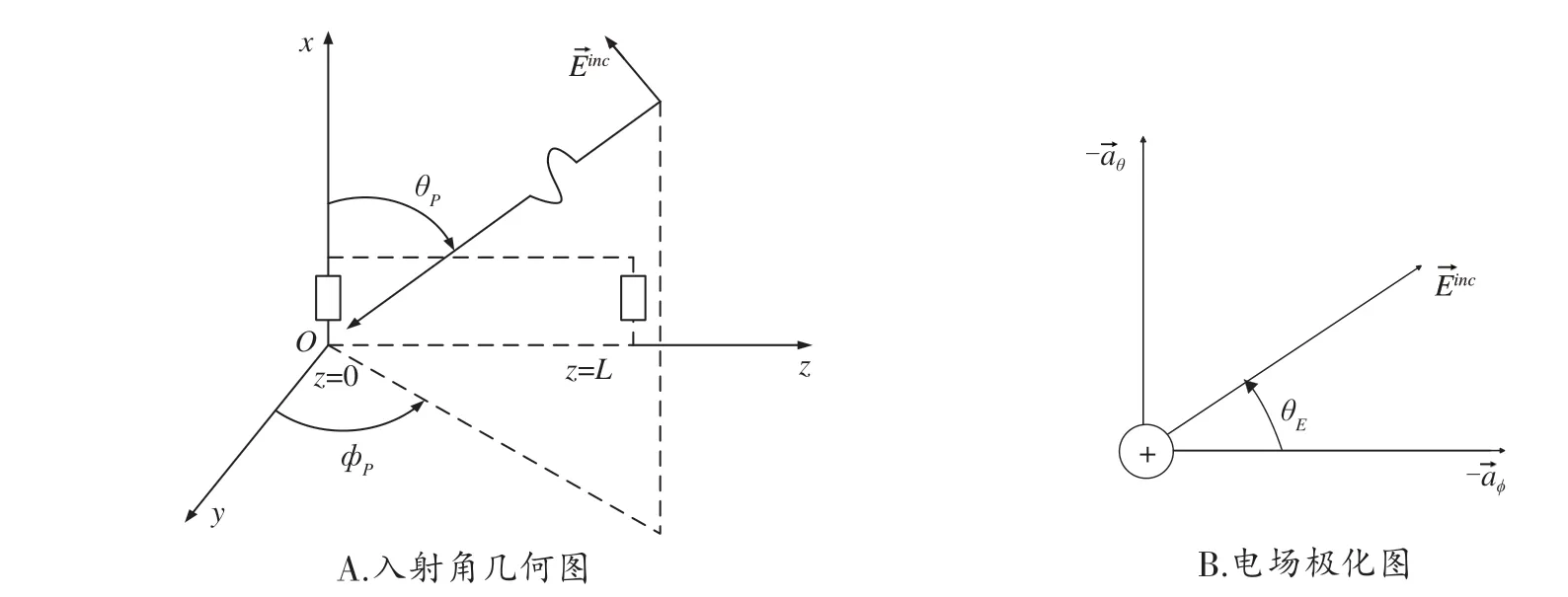
图2 入射波的入射角和极化角图解

根据上述规定，在时谐场情形，传输线直接照射平面波可表示为

其中，E0为照射场幅值分别为直角坐标系x、y和z方向上的单位向量，ex、ey、ez分别为单位入射场在三坐标轴上的分量，可表示为

考虑传输线置于理想导体接地平面上方，入射波不可透入理想导体接地平面内部，只在其表面上发生反射，根据菲涅耳反射定律［16］可知RTE=-1，RTM=1。因此，传输线的直接照射场和背景反射场分别为

本文仅考虑双导体传输线问题，以下分析以y=0 面内的传输线为例进行。在式（1）中，等效激励源ET可表示为

类似地，EL可表示为

其中，d为传输线相对地面的距离，对于近地传输线模型，有sin(βxd)/(βxd) ≈1。将其代入式（7）和（8）后，通过逆傅里叶变换可得

其中，vx、vy、vz表示沿各坐标轴的传播速度，这里

1.2 传输线的离散

下面将基于FDTD 方法，对传输线方程进行离散。电压节点和电流节点在空间分布相距1/2 网格，提取时刻相距1/2 时间步，其节点位置和时间取样如表1所示［17］。

表1 FDTD中电流、电压空间和时间取样

将式（1）中的空间偏导和时间偏导均采用中心差分近似，通过时间步整理后，可得到电压和电流的时间推进公式分别为

1.3 计算域的截断

在传输线的FDTD 分析中，需在终端设置吸收边界条件对计算区域进行截断［17］。本文采用广义戴维南定理结合前后向差分的方案来实现。用IS表示传输线左端(z=0)的电流，IL表示右端(z=L)电流，图3 为传输线左右两端的电压和电流在空间和时间上的离散示意图以及等效电路图。

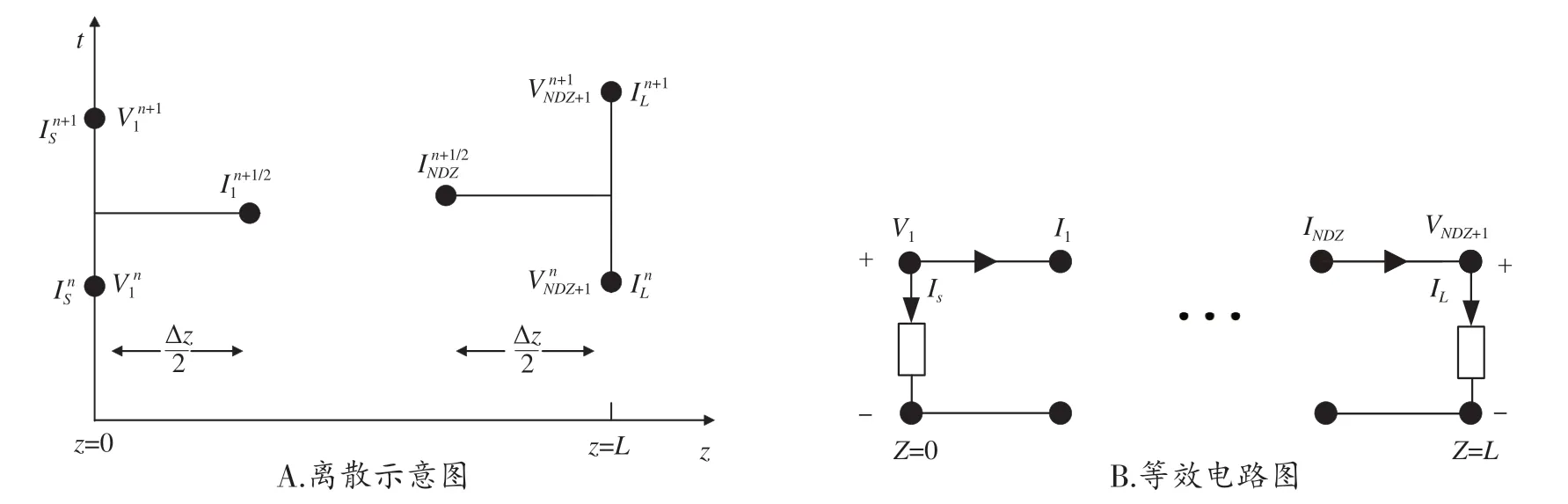
图3 传输线在左右端口空间和时间的离散示意和等效电路图

根据广义戴维南定理［16］可得

将式（15）带入式（14），可得终端吸收边界条件为

其中，V1和I1是传输线左端口处的电压和电流，VNDZ和INDZ是传输线右端口处的电压和电流，RS和RL分别为传输线左右端口的负载阻抗，L=NDZΔz。

2 数值结果与讨论

考虑到传输线模型受到以下HPEM 高斯脉冲激励，

其中，E0=50 KV，t0=0.6 ns，T=0.48 ns。

在以下的计算中，若无特别说明，取传输线长度为10 m，半径为0.38 mm，导线中心之间的距离为1.14 mm。传输线端口负载分别选取为RS1=50 Ω、RL1=1 000 Ω、RS2=10 000 Ω、RL2=100 Ω，单位长传输线分布L和C矩阵分别为

在矩阵L和C中，主对角线元素为传输线的自感和自容系数，其他元素为传输线的互感和互容系数，FDTD 法将空间离散为NDZ=1 000 个网格，每个等间距网格长度Δz=l/NDZ=1 cm（l为传输线的长度），总时间步为NDT=10 000，时间步长Δt=总计算时间/NDT=0.03 ns。

2.1 入射波极化角对传输线端口瞬态响应的影响

以线极化为例，保持其他参量设置不变，仅将入射波的极化角θe分别设置为30°、60°、90°，分析入射波不同极化方向对传输线端口响应的影响，其结果如图4 所示（VL和VR分别表示传输线左端口和右端口的电压瞬态响应）。可以看出，当改变入射波的极化角时，传输线端口的瞬态响应波形几乎相同，只是峰值大小不同。这是由于随着极化角度的减小，电场在传输线横向方向上的分量逐渐减小，从而入射波的电磁场强度幅值不断减小，最终使得线缆终端的响应峰值不断减小。由此可见，传输线上的瞬态响应幅值随着入射波极化角的减小而减小。

图4 传输线端口在不同极化角下的瞬态响应

2.2 入射波入射角对传输线端口瞬态响应的影响

将入射角θp分别设置为30°、60°、90°，分析入射波的入射角对传输线端口的影响情况，其结果如图5所示，其余参数取值与图4相同。可以看出，传输线端口的电压响应在不同入射角下的波动情况大致相同，只是峰值大小和位置有所不同。当入射角度逐渐增大时，响应峰值也有所增大，在入射角为90°时最大。这是由于随着入射角度的增加，电场在传输线纵向方向上的分量逐渐增加，从而入射波的电磁场强度幅值不断增加，最终使得线缆终端的响应峰值增加。因此，传输线上的瞬态响应幅值随着入射角度的增加而增加。

图5 传输线端口在不同入射方向下的瞬态响应

2.3 不同电阻值对传输线端口瞬态响应的影响

由图1 可知，传输线两端的电阻值分别记为RS1、RL1、RS2、RL2。入射波参数设置为θe=60°，θp=60°，φp=-90°，取负载阻值分别为500 Ω、1 000 Ω、2 000 Ω，分析传输线在不同负载阻值下受到入射波激励时，端口瞬态响应的情况，其结果如图6 所示。可以看出，当改变传输线终端的负载阻值时，传输线端口的瞬态响应波形几乎相同，只是峰值大小有所差异。随着终端负载阻值的增大，端口的瞬态响应峰值也随着增大。这是因为当传输线受到一定频率的电磁波照射时，会在传输线上形成感应电流，并通过线缆的阻抗转化为感应电压。由此可以看出，传输线上的电压响应幅值随着终端负载阻值的增加而增加。

图6 传输线端口在不同电阻值下的瞬态响应

3 结束语

本文在传输线方程的基础上，采用FDTD 方法计算了HPEM 高斯脉冲对具有接地负载的多导体传输线的时域电压响应。本方法在整个传输线上进行建模，能够灵活地选取观察点，对任意位置的耦合特征进行分析。在数值模拟过程中充分考虑了地面背景的反射问题，通过数值计算得到了端口电压随入射波照射方向及终端负载变化的基本特性。数值结果对在有外界电磁干扰下，分析设备连接线对终端设备的电磁攻击提供了重要的参考价值。下一步将重点开展高功率电磁波对接地有耗传输线的电磁耦合研究。