分布动载荷频域识别的试验动标定方法研究

罗淑一 姜金辉 张方

引 言

动载荷识别［1？3］是动力学领域的基本问题之一，也是目前亟待解决的难题之一，对结构设计和优化具有重要意义。目前，动载荷识别方法主要可分为时域法和频域法两种。频域法［4？6］的相关研究起步较早，拥有大量的理论方法、研究成果和广泛的实际应用，其数学模型是基于系统外部激励与动响应之间的线性映射关系。频域法为保证识别载荷的精度在所要求范围内，需要信号样本数据具有一定的长度，所以对冲击载荷等短时间的载荷识别会产生较大的误差，降低载荷识别的精度，因此该方法适用于稳态或随机载荷等较长时间的载荷的识别。时域法［7？9］的数学模型是基于系统外部激励与动响应之间的卷积关系，该方法大大降低了信号长度对识别结果的影响，对冲击载荷等短时间的载荷识别较为适用，但由于存在误差传递和误差积累，其识别精度不太理想，且计算效率较低。上述两类方法主要针对集中载荷的识别，由于工程结构的连续性和复杂性，分布动载荷的识别研究相对较少，诸多技术问题和难点亟待解决。

现阶段分布动载荷识别主要通过引入广义正交多项式获得动标定矩阵，从而将分布载荷的识别转化为正交多项式系数的识别，并对载荷进行拟合。目前国内外学者对此进行了研究，已取得了一些研究成果。Karlsson［10］首次讨论了分布简谐力和响应之间的映射关系，并根据此关系对分布动载荷进行识别。Granger 等［11］基于广义正交理论，将作用在一维结构上的分布随机动载荷变换为广义正交级数和的形式进行识别，显著降低了复杂载荷识别的难度。Liu 等［12］提出了一种分布载荷识别的方法——迭代算法，对复合材料层合板表面的瞬态线分布载荷识别进行研究，结果表明该方法在载荷位置识别和时间历程识别上都具有较好的识别效果。Coates 等［13］采用逆插值法对飞行器上作用的分布载荷进行识别，但并未给出具体的研究方法。Wang 等［14］针对不确定的结构模型，采用加速度响应作为系统输入，在时域内结合逆运算和区间运算提出了一种分布载荷识别方法，并验证了所提出方法的高效性和准确性。He 等［15］根据核函数和截断单值分解法对作用在结构声耦合系统上的分布载荷进行识别，通过仿真算例验证了该方法能解决逆过程中的不适定性问题，但并未给出具体的实验验证。Li 等［16］基于泰勒多项式迭代法和三次 Catmull？Rom 样条插值法对分布式动态激励进行时域识别，并研究了该方法的抗噪性能，数值算例表明此方法对载荷识别的精度较高且具有很强的抗噪声性能。Liu 等［17］和 Liu 等［18］研究了其他分布载荷识别方法，这些方法降低了测量误差对载荷识别精度的影响。根据上述研究方法，分布动载荷识别在工程中的应用也越来越广泛。Carne 等［19］提出了一种基于智能变压器和工业计量的分布载荷在线识别方法，该方法在噪声存在的情况下也能正确识别相应载荷，并通过试验对所提出载荷识别方法的识别精度进行了评估。

在目前已有的分布动载荷识别相关研究中，虽然衍生出了不同的分布动载荷识别理论和方法技术，但对其识别过程中的动标定技术却鲜有研究。姜昊［20］利用切比雪夫多项式完成了非接触分布激励的动标定，首次将有限元仿真动标定应用到载荷识别中；徐梅［21］对仿真动标定方法进行拓展，提出了降维思想和分块识别方法，进一步推动了分布载荷识别过程中动标定技术的发展。

然而，上述提到的仿真动标定方法存在明显的局限：一是传统的仿真动标定是基于结构有限元模型来完成的，由于在动标定过程中存在着不可避免的模型误差，导致标定矩阵的不准确，从而使得载荷识别结果精度不高；二是在工程实践中无法直接对工程结构施加正交多项式载荷，在一定程度上增加了仿真标定方法工程应用的复杂性和困难性。因此，本文基于 Legendre 正交多项式和 Gauss？Legend？re 积分提出了分布动载荷频域识别的试验动标定方法，即利用 Gauss？Legendre 积分对标定矩阵离散化，通过测量有限的高斯点和响应点间的频响函数来完成分布载荷识别过程中的动标定，克服传统仿真标定在试验时无法加载正交多项式载荷计算标定矩阵的局限性，进而实现分布动载荷的识别。该方法的主要思想是通过选取适当的高斯点，计算结构上高斯点和响应点之间的频响函数以及相应的 Legendre正交多项式具体值，进而通过组合高斯点和响应点之间的频响函数与 Legendre 正交多项式，求解出具体的试验动标定矩阵，完成相应的动标定过程并识别载荷。数值仿真验证了该方法的有效性，与传统的仿真动标定相比，该方法避免了模型误差对载荷识别精度的影响，具有更高的识别精度，此外，还通过相应的试验进一步验证了本文所提出的试验动标定方法的可行性与工程适用性。

1 一维结构分布载荷识别与试验动标定方法

1. 1 连续梁结构分布载荷频域识别理论

两端简支的连续等截面均质细长 Bernoulli？Eul？er梁如图 1 所示。

上文基于 Legendre 正交多项式讨论了连续梁结构分布载荷的频域识别方法，事实上，Q 间接涵盖了连续梁结构的响应与正交多项式系数之间的传递关系，定义为动标定矩阵。对于现有研究中传统的仿真动标定，Q 是通过在有限元模型上施加正交多项式载荷求解测点响应得到的，然而此种仿真动标定存在模型误差，导致动载荷识别精度不高，且在工程应用中难以直接在实际结构上施加正交多项式载荷，因此，本文基于 Gauss？Legendre 积分提出了試验动标定方法来较好地识别分布载荷。该方法主要是通过选取高斯点，确定高斯点在梁上的具体坐标位置，并计算梁上高斯点和响应点之间的频响函数以及相应的 Legendre 正交多项式具体值，进而通过组合高斯点和响应点之间的频响函数与 Legendre 正交多项式 ，求解出具体的动标定矩阵 ，从而识别载荷。

1. 2 连续梁结构试验动标定方法

本文提出的试验动标定方法可通过下式所示的Gauss？Legendre 积分来实现：

其动标定流程图如图 2 所示。相应地，该动标定过程主要分以下几个步骤来实现：

（1）确定连续梁模型结构及相应的参数。

（2）选取高斯点数，根据高斯积分表确定高斯点值 us 及相应的求积系数值 As。由于高斯点数目对动标定精度有重要影响，进而影响载荷识别精度，因此一般情况下为了提高识别精度，需要适当增加高斯点数。

（3）确定各个高斯点在连续梁结构上的坐标位置，同时也可以确定 Legendre 正交多项式在各个高斯点下的具体值。

（4）根据前一步中计算出的高斯点值，通过仿真计算出式（15）中每个高斯点和响应测点之间的频响函 数 H，再 结 合 Legendre 正 交 多 项 式 的 具 体 值Pˉj （ l/2u + l/2 ），即可求得动标定矩阵 Q。

此外，图 3 给出了现有研究中的仿真动标定的流程图，以便与本文所提出的动标定方法进行仿真对比分析。

2 仿真算例

为验证本文所提出方法的有效性和高精度性，采用图 1 所示的两端简支的等截面均质 Bernoulli？Euler 梁，其上作用有一维分布动载荷 F （ x，t ），根据上文所述的方法识别载荷。分布载荷的识别误差和相应的分布动载荷形式如下式所示：量点，为保证识别精度，一维 Legendre 正交多项式阶数取 7 阶，动标定过程中的高斯点数 N=10。首先考虑响应不含噪声的情况，将本文所述方法与仿真动标定进行对比来评估本方法的优越性，其载荷识别结果及相對误差如图 4（a）～（d）所示；随后分别在响应中添加 5% 与 10% 的随机噪声（加入的噪声幅值大小为响应幅值大小的 5% 和 10%），在相同噪声条件下同样与仿真动标定进行对比分析，识别结果及相对误差如图 5（a）～（h）所示。载荷识别相对误差对比如表 2 所示。

由图 4（a）～（d）中可以看出，针对本文所提出的动标定方法，在无噪声干扰时，识别载荷与真实载荷沿整个梁长的分布曲线完全重合，仅在梁的两端简支处略有偏移，但是两端简支处的相对误差不超过0.45%，整个分布载荷的相对误差不超过 0.05%，识别精度相对较高。针对仿真动标定，其识别结果虽然同样与真实载荷完全重合，但其相对误差略大于本文所提出的动标定方法，由此表明本文所提出的方法在分布载荷识别上更具有优势。

图 5（a）～（h）分别表示响应中添加 5% 和 10%噪声的载荷识别结果，结合表 2 可以看出，当响应中添加 5% 和 10% 噪声时，本方法中虽然识别误差增大，但其最大相对误差分别为 1.29% 和 6.78%，平均相对误差分别为 0.33% 和 2.4%，误差在可接受的范围内，且整体载荷的趋势与真实值是相吻合的。此外 ，对比本方法与仿真动标定方法 ，可以看出在10% 噪声干扰下，仿真动标定最大相对误差和平均相对误差分别为 10.56% 和 3.95%，远远高于相同噪声条件下本方法的误差值，表明利用仿真动标定方法得到的识别结果精度受噪声影响较大，其抗噪性能低于本方法，进一步表明试验动标定方法在载荷识别方面更具有优势。

根据图 6（a）～（l）以及表 3 可以看出，三种不同高斯点数下的实部平均相对误差分别为 0.00067%，0.011% 和 0.094%，虚 部 平 均 相 对 误 差 分 别 为0.044%，0.44% 和 1.49%；当高斯点数 N = 10 时，其载荷识别效果最好。综合上述三种情况可以看出，高斯点数越多，相对误差越小，其识别结果精度越高，因此适当增加高斯点数有利于提高识别精度。

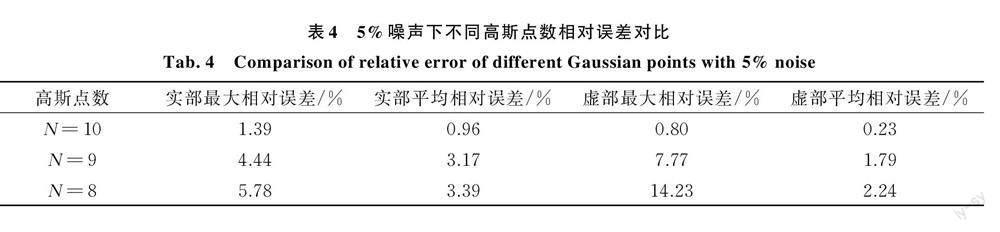
保持所有参数不变，在响应中添加 5% 的随机噪声，其载荷识别结果如图 7（a）～（l）所示，相对误差对比如表 4 所示。

根据图 7（a）～（l）以及表 4 可以看出，三种不同高 斯 点 数 下 的 实 部 平 均 相 对 误 差 分 别 为 0.96%，3.17% 和 3.39%，虚部平均相对误差分别为 0.23%，1.79% 和 2.24%。由此可见，随着高斯点数的减少相对误差大大增加，同时抗噪性逐渐降低，因而在相同噪声条件下适当增加高斯点数是保证抗噪性的关键，可以提高识别精度。

3 试验验证

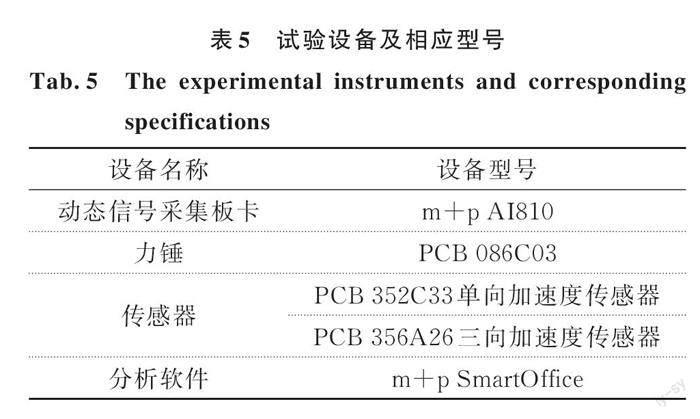
上文对分布载荷识别过程中的试验动标定技术进行了详细的研究，并通过仿真算例验证了本方法的正确性，为进一步验证试验动标定方法的有效性，下文通过试验与仿真相结合的方法完成了相应的载荷识别工作，所涉及到的试验设备及相应型号如表5 所示。

本次试验所用到的试验件为简支梁，其相应的简支梁模型参数如表 6 所示。为获得简支梁的模态参数，通过锤击法完成了相应的模态试验。模态试验中采用力锤激励，选取单向加速度传感器采集信号，并设置采样率为 2048 Hz，测得简支梁前四阶固有频率和阻尼比，并与仿真分析得到的固有频率进行对比，如表 7 所示。

根据表 7 可知，模态试验得到的固有频率与有限元仿真计算得到的频率较为接近，且前四阶相对误差均小于 1%，表明所建立的有限元模型较为准确，可以通过仿真计算来获取测点的响应信息，作为载荷识别的已知条件。

在动标定试验中，同样选择加速度传感器采集信号，所用到的试验设备和仪器如表 5 所示。动标定试验的目的是通过激励高斯点获取动标定矩阵 Q中的传递函数 H；此外，当高斯点确定时，动标定矩阵 Q 中的 Legendre 正交多项式也随之确定。本次试验中选择 11 个高斯点分别进行激励，并采集简支梁上 9 个测量点的响应，从而获得高斯点和各个响应点之间的传递关系，进而再结合 Legendre 正交多项式求解出具体的动标定矩阵。试验过程中激励点与响应点的位置如图 8 所示，动标定试验图和动标定试验流程图分别如图 9 和 10 所示，试验测得的各高斯点和响应点之间的频响函数图如图 11 所示。

根据所建立的有限元模型，假设作用在简支梁上的分布载荷为 f =（ 5x2 + x ） sin （ 2π × 150t ），通过仿真分别计算出如图 8 所示的响应点位置处的频域响应数据，结合动标定试验所获得的动标定矩阵 Q，取 Legendre 正交多项式阶数为 7 阶，得到作用在简支梁上的分布载荷识别结果和相对误差分别如图12 和 13 所示，相对误差对比如表 8 所示。

根据图 12，13 以及表 8 可以看出，针对载荷幅值识别，其识别值与真实值之间的最大相对误差为13%，平均相对误差为 1.2%。最大相對误差出现在简支梁两端处，其原因是由于边界条件的约束，使得结构动响应与频响函数的数值均较小，当响应出现较小的扰动时，载荷识别的结果变化比较剧烈，因此相较于简支梁中间处，两端处的识别效果较差。虽然识别值与真实值的空间分布图不是完全重合的，但整体的空间分布趋势是吻合的，且相对误差在可接受的范围内。根据识别结果，本文所提出的试验动标定方法可以很好地识别作用在结构上的分布动载荷，解决了实际工程应用中无法施加正交多项式载荷的局限性，降低了工程应用的复杂性。

4 结 论

本文基于 Legendre 正交多项式和 Gauss？Legen？dre 积分，通过合理地选取高斯点，建立了分布载荷频域识别的试验动标定方法。数值仿真将该方法与传统的仿真动标定方法进行对比分析，在 10% 噪声干扰下该方法与仿真标定的最大相对误差分别为6.78% 和 10.56%，表明在相同噪声条件下仿真标定的识别精度要低于本方法，验证了本方法的有效性和高精度。同时，还研究了不同高斯点数对载荷识别精度的影响，仿真结果表明，适当增加高斯点数可以提高载荷识别精度，增强抗噪性。此外，还通过相应的试验进一步验证了该方法的可行性与工程适用性。

参考文献：

［1］ Law S S， Zhu Q X， Zeng Q H， et al. Regularization in moving force identification ［J］. Journal of Engineering Mechanics，2001，127（2）：136-148.

［2］ 周盼，张权，率志君，等 . 动载荷识别时域方法的研究现状与发展趋势［J］. 噪声与振动控制，2014，34（1）：6-11.

Zhou Pan， Zhang Quan， Shuai Zhijun， et al. Research status and development trend of time domain method for dynamic load identification［J］. Noise and VibrationControl，2014，34（1）：6-11.

［3］ 杨智春，贾有 . 动载荷识别方法的研究进展［J］. 力学学报，2015，47（2）：384.

Yang Zhichun， Jia You. Research progress of dynamic load identification methods［J］. Chinese Journal of The？oretical and Applied Mechanics，2015，47（2）：384.

［4］ Liu J， Meng X H， Zhang D Q， et al. An efficient meth？od to reduce ill-posedness for structure dynamic load identification［J］. Mechanical System and Signal Pro？cessing，2017，95：273-285.

［5］ 张玉良，杨飞，岳洪浩，等 . 基于频域法的星箭连接分离 装 置 的 冲 击 载 荷 识 别［J］. 振 动 与 冲 击 ，2018，37（17）：79-85.

Zhang Yuliang， Yang Fei， Yue Honghao， et al. Impact load identification of device for satellite and rocket con？nection and separation based on frequency domain meth？od［J］. Jourmal of Vibration and Shock，2018，37（17）：79-85.

［6］ Jia You， Yang Zhichun， Liu Erqiang， et al. Prediction of random dynamic loads using second-order blind source identification algorithm［J］. Journal of Mechani？cal Engineering Science，2020，234（9）：1720-1732.

［7］ Lu Z R， Law S S. Identification of system parameters and input force from output only［J］. Mechanical Sys？tems & Signal Processing，2007，21（5）：2099-2111.

［8］ Jiang Jinhui， Ding Ming， Li Jun. A novel time-domain dynamic load identification numerical algorithm for con？tinuous systems［J］. Mechanical Systems and Signal Processing，2021，160：107881.

［9］ Jiang Jinhui， Luo Shuyi， Mohamed M S， et al. Real time identification of dynamic loads using inverse solu？tion and Kalman filter［J］. Applied Sciences，2020，10（19）：6767.

［10］ Karlsson S E S. Identification of external structural loads from measured harmonic responses［J］. Journal of Sound and Vibration，1996，196（1）：59-74.

［11］ Granger S， Perotin L. An inverse method for the identi？fication of a distribution random excitation acting on a vi？brating structure part 1： theory［J］. Mechanical Systems and Signal Processing，1999，13（1）：53-65.

［12］ Liu G R， Ma W B， Han X. An inverse procedure for identification of loads on composite laminates［J］. Com？posites Part B： Engineering，2002，33（6）：425-432.

［13］ Coates C W， Thamburaj P. Inverse method using finite strain measurements to determine flight load distribution functions［J］. Journal of Aircraft， 2008， 45 （2） ：366-370.

［14］ Wang Lei， Liu Yaru， Liu Yisi. An inverse method for distributed dynamic load identification of structures with interval uncertainties［J］. Advances in Engineering Soft？ware，2019，131：77-89.

［15］ He Z C， Lin X Y， Li E. A non-contact acoustic pres？sure-based method for load identification in acoustic structural interaction system with non-probabilistic un？certainty［J］. Applied Acoustics，2019，148：223-237.

［16］ Li Xiaowang， Zhao Haitao， Chen Zheng， et al. Identifi？cation of distributed dynamic excitation based on Taylor polynomial iteration and cubic Catmull？Rom spline inter？polation［J］. Inverse Problems in Science and Engineer？ing，2020，28（2）：220-237.

［17］ Liu He， Liu Quansheng， Liu Bin， et al. An efficient and robust method for structural distributed load identifi？cation based on mesh superposition approach［J］. Me？chanical Systems and Signal Processing，2021，151：107383.

［18］ Liu J， Li K. Sparse identification of time-space coupled distributed dynamic load［J］. Mechanical Systems and Signal Processing，2021，148：107177.

［19］ Carne G D， Bruno S， Liserre M， et al. Distributed on？line load sensitivity identification by smart transformer and industrial metering［J］. IEEE Transactions on In？dustry Applications，2019，55（6）：7328-7337.

［20］ 姜昊 . 非接觸分布激励下的动态标定技术［D］. 南京：南京航空航天大学，2009.

Jiang Hao. Dynamic calibration technique under non contact distributed excitation［D］. Nanjing： Nanjing University of Aeronautics and Astronautics，2009.

［21］ 徐梅 . 复杂结构分布载荷识别的动态标定技术研究［D］. 南京：南京航空航天大学，2009.Xu Mei. Research on dynamic calibration technology for distributed load identification of complex structures［D］.Nanjing： Nanjing University of Aeronautics and Astro？nautics，2009.

［22］ 李庆扬，王能超 . 数值分析［M］. 5 版 . 北京：清华大学出版社，2008.

Li Qingyang， Wang Nengchao. Numerical Analysis［M］. 5th ed. Beijing： Tsinghua University Press，2008。