追求自然的数学教学——苏科版数学教材八（下）第五章“平面直角坐标系”教学过程分析

■陈磊

本节课是苏科版数学教材八年级下册第五章第二节的第一课时。平面直角坐标系是初中教材中的基础性知识，是串联“数”与“形”的重要载体，旨在构建点与有序实数对的对应关系，实现一维向二维的转变。本课主要从学生的生活、数学学习经验出发，建立新旧知识的联系，关注学生概念自然生成的过程，培养学生的数学思维。

一、问题引导，激活旧知

问题1：有关七年级所学的数轴，同学们还记得哪些内容？

新课伊始，教师设计开放性的问题，让学生各抒己见，在调动学生积极性的同时，指引学生深度回顾，为后续知识的自然生长打下基础。

问题2：（教师给出一个数轴，如图1）请同学们思考：（1）数-2、0、3 在数轴上是如何表示的？（2）数轴上的点P又如何表示？

图1

学生旧知被激活后，教师从问题出发，让学生回顾实数与数轴上的点一一对应，激活实数与点之间的联系，让学生重温数形结合的思想。

二、情境引入，生活感知

问题3：2023 年春节档国产电影好评如潮，同学们都看了吗？小丽也买了一张电影票，她如何在电影院快速地找到座位？

对国产电影的肯定，能激发学生的自豪感和爱国情怀，起到学科育人目的；从学生实际生活出发，设置问题情境，让学生初步感悟描述位置的关键点，为后面数学问题的研究创造条件。

三、经历过程，生成概念

问题4：数学中，如何确定一个点在平面内的位置？（教师在黑板右上角放一个小磁力贴，记为点A）请同学们描述黑板平面内点A的大致位置。

大多数学生很快能根据生活经验，不经思索“蹦”出答案：“右上角。”这说明对于八年级学生而言，他们通过生活经验的积累，脑子里已经有了“隐形的平面直角坐标系”。“右”的描述，其实说明在其脑海里已经有了竖直的一条线；“上”的描述，其实说明在其脑海里也已经有了水平的一条线。这样通过对学生生活经验的唤醒，引出接下来要研究的数学内容，自然生成，而不是教师强拉硬拽。

在学生回答后，教师在黑板上画出两条相互垂直的直线。

问题5：刚才回答“右上角”很对，请小组交流如何更准确地描述该点在黑板平面的位置。

学生上黑板度量，量出该点到两直线的距离，得出用两个实数来表示的初步结论。

问题6：能将这两个数据换个位置吗？作点A关于竖直的直线的对称点，那该对称点又该如何描述呢？

通过问题串铺设，让学生结合生活经验，先感悟有序，然后，面对“点A与所对应的有序实数对一样”这个实际困难，学生自然想到用正、负来区别，顺理成章地将已学数轴迁移到新知识的建构中来，自然地将两条垂直的直线“生长”为两条具有公共原点的相互垂直的数轴，生成平面直角坐标系、x轴、y轴、坐标原点等概念。

四、回顾历史，感受文化

弗赖登塔尔曾强调对历史的运用要体现“再创造”的过程，平面直角坐标系的发展最初起源于圆锥曲线研究的桎梏。对于八年级学生来说，这样的历史背景虽不能完全理解，但在教师解读后，学生也能感受在历史长河中平面直角坐标系产生的“自然”。另外，为激起学生的学习兴趣，增加学习的趣味性，教师渗透笛卡尔观察蜘蛛网从而发明了坐标系的故事，鼓励学生在生活中多观察，多思考，多感悟。

五、问题探究，深入理解

问题7：如何在平面直角坐标系中表示点A、B、C的位置？

如图2，学生动手操作，由A点向x轴、y轴作垂线，垂足M在x轴上的坐标是3，垂足N在y轴上的坐标是4，我们说点A的横坐标是3，纵坐标是4，有序数对（3，4）就叫作点A的坐标，记作A（3，4）。以此类推，点B的坐标为（-2，1），点C的坐标为（-3，-3）。

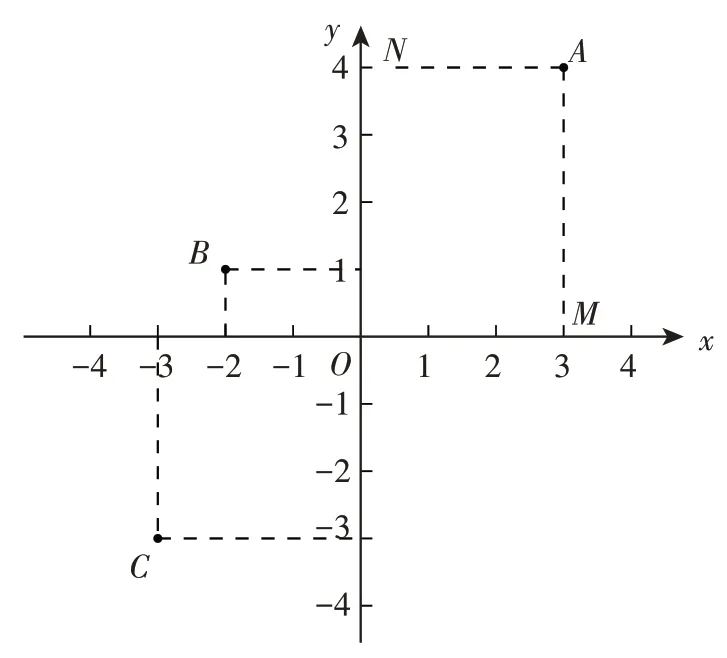
图2

问题8：怎样在平面直角坐标系中描出点（2，3）、点（-1，3）、点（2，-2）？

学生画出图形，归纳作图方法：先在x轴上找到表示2 的点，再在y轴上找到表示3的点，过这两个点分别作x轴、y轴的垂线，两条垂线的交点就是点（2，3）。

问题9：数轴上的点与实数一一对应。通过刚才的研究，平面直角坐标系中的点跟什么存在对应关系呢？

教师引导学生从问题7 感悟平面内任意一点对应唯一一个有序实数对，反过来，通过问题8 感悟任意一个有序数对也对应唯一的一点。学生在动手动脑的同时自然感悟坐标平面内的点与有序实数对一一对应的关系。

问题10：观察平面内不同位置的点，说出它们的坐标，并归纳出这些点的坐标分别具有什么特征。

学生在探究中，通过观察、操作、归纳，最后得出结论，既是对数学概念的深入理解和掌握，也培养了分类的意识。

六、反思归纳，迁移延伸

问题11：请同学们带着问题，回顾和总结本节课所学：

（1）什么是平面直角坐标系？

（2）数轴与平面直角坐标系的异同点有哪些？

（3）平面直角坐标系内的点与坐标之间有什么关系？

（4）平面直角坐标系将平面分成了几个部分？每个部分的点的坐标有什么特点？

通过几个问题，让学生对本节课的知识进行梳理、归纳，并与之前所学的数轴知识建立联系，通过对比，形成理性认识，将新知转化为自己的认知。

问题12：大家观察我们的教室空间，在我们这个教室空间里，对于讲台上的这个小粉笔头（看成一个点），又该如何描述它的位置呢？

本节课学生通过探究，由一维走向了二维，自然会思考：三维位置又该如何表述？作为本节课的延伸，笔者让学生课后查阅资料，自主探究，丰富学生的课后学习，也让学生对未来的学习充满期待。

夸美纽斯曾强调，我们的教学应遵循自然规律。数学概念的教学，是数学的逻辑起点，其产生与发展存在着自然性。我们的课堂在情境设置、问题串的设计等方面要立足学生的“最近发展区”，围绕知识和能力的本质，以提升学生学科素养为目的，合情合理，追求自然。