一类新的广义Gauss和及其四次均值

陈 丽

(西安财经大学 数学学院,陕西 西安 710100)

令q是整数,χ表示模q的任意Dirichlet特征,对于任意的整数a、b和c,介绍下面一种新的和式,即广义Gauss和G(a,b,c,χ;q),定义如下。

G(a,b,c,χ;q)=

其中,e(y)=e2πiy,i2=1。

不难看出,如果a=c=0,b=1,那么,G(0,1,0,χ;q)=τ(χ);如果b=c=0,(a,q)=1,那么,G(a,0,0,χ;q)=χ(a)·τ(χ2)。显而易见,它们都是经典的Gauss和,因此,把G(a,b,c,χ;q)称为新的广义Gauss和。并且,完全可以证明G(a,b,c,χ;q)是一个广义Kloosterman和(具体证明参阅第1节引理2)。为了寻找这些和式之间的潜在关系,研究G(a,b,c,χ;q)的各种数论性质是极其必要且有意义的。

本文将研究广义Gauss和G(a,b,c,χ;q)的均值计算问题,并给出在q=p且q为一个奇素数时,G(a,b,c,χ;q)的四次均值的一个精确计算公式,最终完成定理1的证明。

定理1令p是奇素数,a和b是2个整数且(a,p)=1。则对模p的任意阶非主特征χ,下面的恒等式可以被给出,即

注1本文只研究了G(a,b,c,χ;p)在最为简单情形下的四次均值的计算问题。而对于任意整数k≥3,是否存在2k次均值的一个精确的计算公式?还是一个公开的问题。建议感兴趣的读者可以一起研究。

不难看到,如果χ是模p的主特征χ0,那么,G(a,b,c,χ0;p)就成为普通的三角和,这时其值的模长为常数,因此结果是平凡的。针对这种情况没有必要去考虑。

除此之外,如果条件是一般的整数q≥3,是否也存在与定理1类似的结果?这也是一个有趣的问题,需要做进一步的考察。

1 若干引理

为了证明本文中所给的定理1,在这一部分,需要给出3个简单的引理。本节会多次用到很多初等数论和解析数论的相关知识,经典Gauss和以及Dirichlet特征的主要性质,有关这些知识点的具体内容在文献[1-3]中均有详细的介绍,这里不再罗列。

引理1令p是奇素数,则对任意整数k、a、b,且(ka,p)=1,有下面的三角恒等式

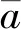
证明由模p的简化剩余系的性质并经过整理,有

(1)

其次,对任意整数c且(c,p)=1,由勒让德符号的性质,有

(2)

结合式(1)和式(2),有

引理1证毕。

引理2令p是奇素数,a和b是任意的2个整数且(a,p)=1。则对模p的任意阶非主特征χ,有

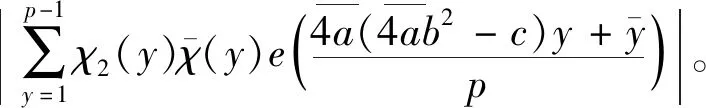
证明根据经典Gauss和的性质及引理1,可得

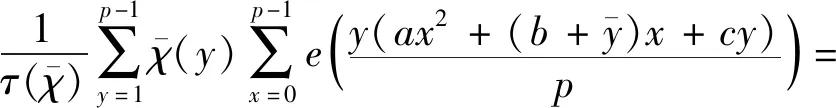
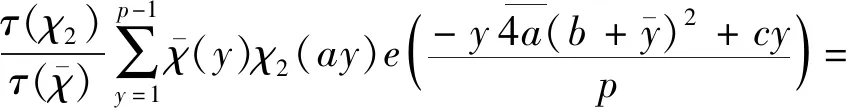
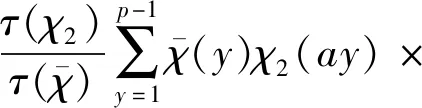
(3)

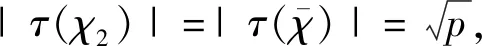
引理2证毕。

引理3令p是奇素数,χ是模p的任意阶Dirichlet特征。则对任意的整数n且(n,p)=1,可以给出

证明证明过程可参阅文献[4-5]。与广义Kloosterman和有关的其它文章均可参阅文献[6-14]。

2 定理1的证明

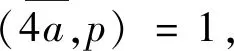
(4)

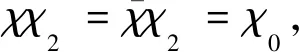
根据式(4)和引理3,有

1+2p3-3p2-3p-1=

2p3-3p2-3p

(5)

再从式(4)和引理3,可以推出

p2+2p3-7p2=

2p3-6p2

(6)

最后,将式(5)和式(6)结合,即可得到定理1的内容。

3 结语

本文通过研究一类新的广义高斯和的均值问题,计算得到了它的四次均值的一个新的公式。即在任意整数a和b,且(a,p)=1的条件下,得到了计算公式

通过研究可以看出,该结果是有意义且有必要的,它不仅扩充了解析数论中的两大著名和式经典Gauss和与Kloosterman和的研究内容,同时也为该领域的进一步发展做出了新的贡献。

另外,本文也提出了解析数论领域中需要进一步研究的几个问题,这些都有助于该领域研究工作的进一步展开。