基于多元线性回归的烘丝出口水分影响因素的研究

梅 芳，王世旭， 曹林海，陈卓骥，朱科侦，王 巍

（湖北中烟工业有限责任公司，湖北武汉 430000）

烘丝工序是制丝线上的关键工序，有研究表明，可以通过不断优化烘丝工序关键工艺参数的方式和调控模式，平衡湿热处理强度，进而达到稳定烘丝出口水分，并兼顾叶丝的内在卷烟品质和物理感官品质，是现阶段烘丝工序工艺研究的重要方向[1]。

1 工作原理

滚筒式烘丝机工作原理：烟丝经过加温加湿后由振动输送机送入烘丝筒内，热风系统按一定比例设置分为两路流向，一路热风从进料端顶部输送到筒内，与烟丝形成顺向流动并与烟丝充分接触，实现热气流的排潮干燥，后续流至出料端顶部的排潮口排出；另一路热风由进料端送入筒内，对烟丝直接进行预热处理[4]。烟丝在圆形空间内通过炒料板的作用不断翻滚下落，同时与筒体加热管板及热风充分接触，达到干燥水分的目的，并从出料端排出。

烘丝机工作原理图见图1，烘丝机运行工艺参数见表1。

表1 烘丝机运行工艺参数

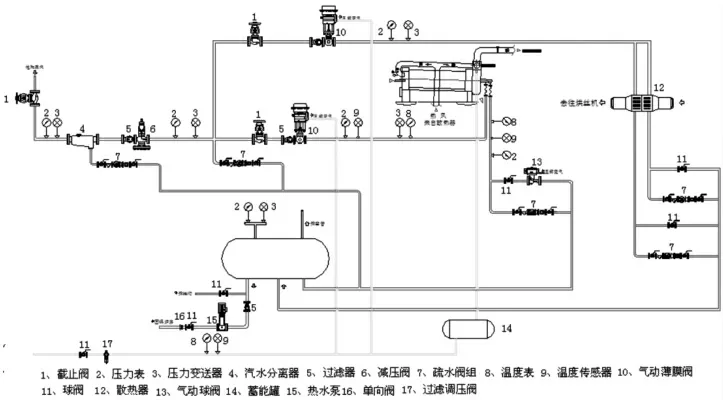
图1 烘丝机工作原理图

在武汉卷烟厂KA2 类卷烟工艺运行参数下，稳定筒壁温度的同时，如何合适地调整热风风速，以达到稳定烘丝出口水分的目的，对卷烟产品质量均质化有着至关重要的作用。

2 多元线性回归分析

2.1 初步构建回归方程

依托MES[5]系统（Manufacturing Execution System，制造企业生产过程执行系统），选取某牌号30 个批次的烘丝工序生产过程工艺运行参数：HT 入口烟丝含水率、出口叶丝含水率、HT 蒸汽压力、筒壁温度、热风风速、排潮负压（见表2），进行多元线性回归分析，利用Minitab 软件通过数据分析初步构建回归方程：出口叶丝水分=13.6+0.476HT 入口含水率- 2.67 热风风速- 0.074 4 筒壁温度+ 7.21HT 蒸汽压力- 0.004 79 排潮负压。

表2 30 批次烘丝机运行参数数据

验证出口叶丝含水率与HT 入口烟丝含水率、热风风速、HT 蒸汽压力、筒壁温度、排潮负压之间是否有相关性。

30 批次烘丝机运行参数数据见表2，Minitab 软件运行得出的回归方程及残差图见图2。

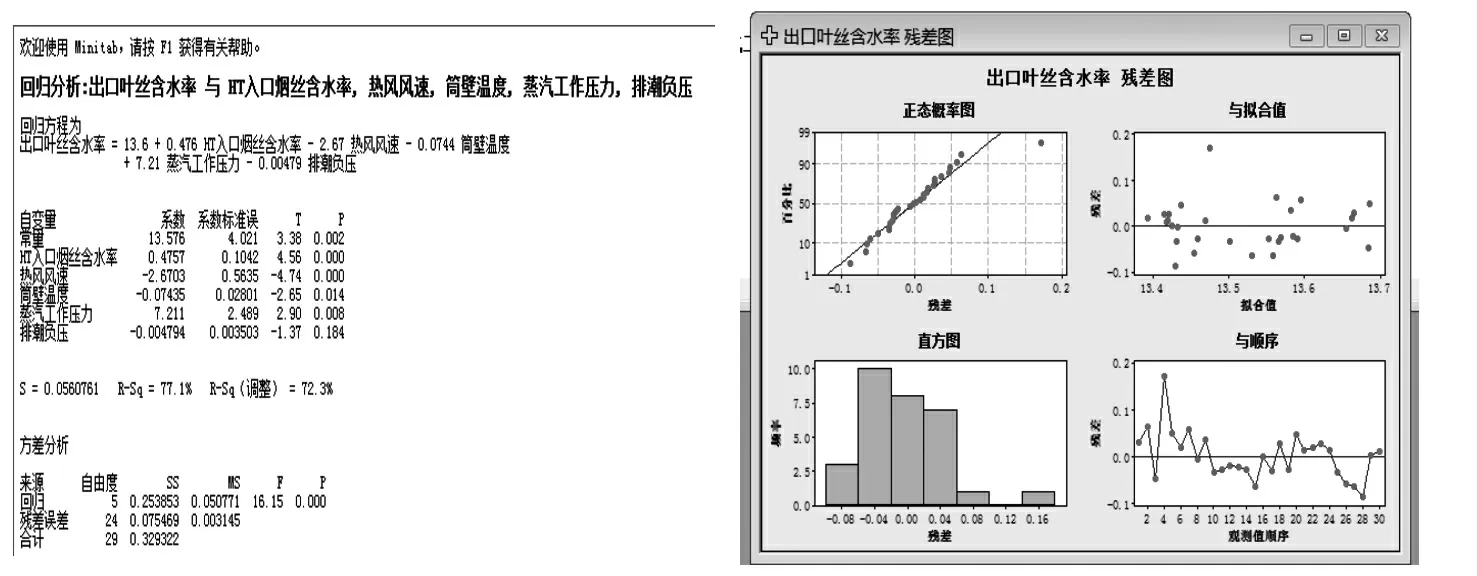
图2 Minitab 软件运行得出的回归方程及残差图

从图2 中可得出以下结论：

（1） 结合ANOVA 表分析回归方程总的显著性检验结果，由于p 值=0.002 ＜α =0.05，表明在显著显著性水分α=0.05 下，线性回归方程总效果是显著的。

（2） 回归模型显著性的度量指标：从R-Sq=77.1%，R-Sq（调整）=72.3%来看，二者很接近，S=0.056 076 1。

（3） 各个参数回归系数的显著性检验，从回归系数检验来看，自变量HT 入口烟丝含水率、出口叶丝含水率、HT 蒸汽压力、薄板温度、热风风速p 值均小于α=0.05，故这4 个因子均为显著因子；自变量排潮负压的p 值= 0.184 ＞α= 0.05，效应不显著，说明该因子不显著。

（4） 进行残差分析。通过图2 的四合一残差图，均显示正常。

经过以上分析，设定的线性回归模型是可以接受的，只是从方程中删除不显著变量“排潮负压”。

2.2 修正回归方程模型

Minitab 软件运行得出的回归方程及残差图见图3。

图3 Minitab 软件运行得出的回归方程及残差图

删除自变量排潮负压，修正模型（见图3），可以得出HT 入口烟丝含水率、出口叶丝含水率、HT蒸汽压力、筒壁温度、热风风速的回归方程为：出口叶丝水= 12.4 + 0.501HT 入口含水率- 2.97 热风风速- 0.063 筒壁温度+ 6.14HT 蒸汽压力。

从图3 中可得出以下结论：

（1） 结合ANOVA 表分析回归方程总的显著性检验结果，由于p 值= 0 ＜α = 0.05，表明在显著性水分α=0.05 下，线性回归方程总效果是显著的。

（2） 回归模型显著性的度量指标：从R-Sq=71.8%，R-Sq（调整） = 67.3%，模型可以，从S=0.060 9 比较小，可以容忍。

（3） 各个参数回归系数的显著性检验，从回归系数检验来看，p 值均小于α=0.05，效应显著，说明因子均显著。

（4） 进行残差分析。通过图3 的四合一残差图，均显示正常，

经过以上分析，认定的线性回归模型是可以接受的，认定修正后的模型为：出口叶丝水= 12.4 +0.501HT 入口含水率- 2.97 热风风速- 0.063 筒壁温度+ 6.14HT 蒸汽压力。

3 应用效果

在实际生产过程中，HT 蒸汽压力保持0.15 MPa和筒壁温度维持135 ℃不变时，当HT 入口烟丝含水率在18.4%～19.0%波动时，对照热风风速稳定实际值和预测热风风速值可看出，预测热风风速平均差值为0.006。

烘丝机热风风速对比见表3。

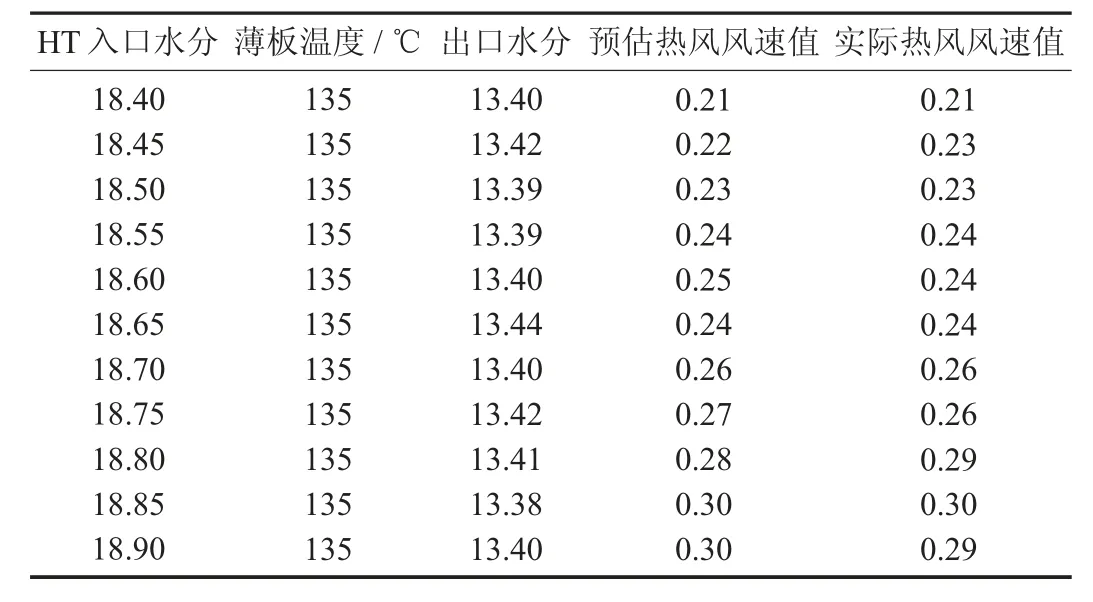
表3 烘丝机热风风速对比

由表3 可知，此回归方程模型可以有效指导烘丝工序实际生产过程中及批次间，HT 入口水分变化时对应热风风速的调整。