熔喷双槽形喷嘴内部通道气体流场数值模拟

姜莹莹 陈廷

摘要：熔喷双槽形喷嘴气槽出口处宽度方向上的气体速度分布均匀性受内部气流通道结构的影响。为探究喷嘴内部通道结构对气体速度分布均匀性的影响，采用数值模拟的方式对喷嘴内部气流通道的气体流场进行数值计算。用ANSYS软件中的Workbench平台建立出贴合实际的三维流场模型，并划分出符合网格质量要求的网格。在Fluent软件中设置求解器类型及定义边界条件，进行数值计算。结果表明：气体在由气腔1流入通气孔A时，在通气孔A1至A4出口处的速度峰值及温度谷值各有不同，分布趋势表现为越靠近喷嘴外侧的气孔出口处速度峰值越大、温度谷值越小，越靠近喷嘴中部的气孔出口处速度峰值越小、温度谷值越大。且通气孔B出口处的速度峰值及温度谷值受通气孔A的影响，也呈现出与通气孔A出口处相同的分布趋势。

关键词：熔喷双槽形喷嘴；气体流场；内部通道；数值模拟

中图分类号：TS174.1

文献标志码：A

文章编号：1009-265X（2023）02-0072-08

熔喷法是借助高速高温气流使刚挤出的高聚物熔体迅速拉伸固化成形的纺丝方法，优点是工艺流程短，可以直接制成无纺织物。熔喷布具有空隙多、结构蓬松、抗褶皱能力好等特点，在过滤材料、隔离材料、口罩材料及擦拭布等领域有着广泛的应用。

熔喷喷嘴的工艺参数对拉伸气流的速度大小和分布均匀性有很大的影响，国内外有多位学者对熔喷喷嘴的气体流场进行了研究，并对喷嘴进行了改进。Harpham等［1-2］首次对双槽形喷嘴气体流场的速度分布进行了实验研究，分析得到了拉伸气体速度分布的回归方程。Tate等［3］和Harpham等［2］将熔喷双槽形拉伸热空气体流场分为了3个区域，分别是两股射流汇合前的区域、合并区域及两股射流合并后完全变为一股的区域。Krutka等［4］用计算流体力学软件对拉伸空气体流场进行了数值计算，总结出了3个区域的流场特点。陈廷等［5］建立了喷嘴中线上的拉伸气流速度理论公式，并首次将聚合物拉伸模型的数值模拟结果与气体流场的理论计算结果结合起来。在此之后，陈廷［6］研究了气槽角度、气槽宽度和头端宽度等参数对拉伸热空气的速度和温度分布的影响。Xin等［7］探究了气缝角度对流场的影响。Xie等［8］对拉伸气体流场进行了测量并分析了速度和温度的波动情况。姬长春等［9］对熔喷喷嘴喷气孔端面进行三维数值模拟，探究了端面对气体流场及纤维拉伸工艺的影响。周梓豪等［10］对制备碳纳米管纤维所用的直立式气相沉积反应器气体流场进行了数值模拟，刘宏霞等［11］建立了气相沉积反应器内的纤维/气体两相流动模型，模拟了纤维的运动形态。

前人对于熔喷双槽形喷嘴的研究多集中于喷嘴外部拉伸空气气体流场，探究拉伸气流对熔喷纤维直径大小的影响。然而在实际生产中还存在着在喷嘴幅宽方向上所制备纤维直径存在差异的问题，该问题由喷嘴幅宽方向上气流速度及温度的分布不均匀性引起，探究喷嘴内部气流通道对气体流场的影响有助于解决这一问题。本文将建立喷嘴内部通道流体域的三维模型，采用数值模拟的方法探究喷嘴内部气流通道对气体流场的影响。

1气体流场的几何模型

由于喷嘴内部气流通道较为复杂，为能够准确地还原喷嘴内部通道气体流场的实际情况，研究内部气体流场的速度分布与温度分布，本文对气体流场进行了三维建模。本文所研究的喷嘴模型是沿中心轴线左右对称的，故在几何建模的时候，只需建立出对称轴一侧的几何模型进行数值模拟即可。

图1为熔喷双槽形喷嘴的结构示意图，气槽与水平面的夹角为60°，宽度为0.5 mm，喷丝孔的宽度为0.5 mm。图2为喷嘴内部通道结构图，气体由气腔1两侧的入口进入喷嘴内部，依次流经气腔1、通气孔A、气腔2、通气孔B、梯形气腔，最后由气槽流出喷嘴，形成拉伸气流。图3为喷嘴内部气流通道的尺寸图，其中，气槽宽度为0.5 mm，梯形气腔与气槽的夹角为120°。在空气流体力学中，气体经过截面积减小的管道可获得流动的动力，本文所研究的熔喷喷嘴模型中，通气孔A、通气孔B及气槽的截面积逐层减小，为气体加速的主要部分。气槽宽度受到截面积大小的制约，设计为0.5 mm。图4为通气孔A中各气孔的孔距尺寸图。通气孔A由7个形状不同、大小不同的气孔组成，将对称轴一侧的气孔从左往右编号为通气孔A1、通气孔A2、通气孔A3，通气孔A4。其中，通气孔A1为椭圆孔，长轴为10.0 mm，短轴为6.0 mm（沿z轴方向为长轴）。通气孔A2为椭圆孔，长轴为6.6 mm，短轴为5.0 mm。通气孔A3为椭圆孔，长轴为6.0 mm，短轴为5.0 mm。通气孔A4为圆孔，直径为5.0 mm。通气孔B由30个直径为2.2 mm的小圆管组成，将对称轴一侧的小圆管从左往右依次编号为通气孔B1至通气孔B15。图5为建立好的熔喷双槽形喷嘴内部通道气体流场三维模型。

2数值模拟

2.1网格划分

在ANSYS Mesh中进行的工作主要有两部分：对各边界命名及网格划分。边界命名示意图如图6，其中，A、B、C、D分别对应inlet、outlet、wall、symmetry。

空气具有一定的黏性，绕流物体时，在贴近物面处形成边界层。由于在边界层处流体的流动速度变化较为复杂，流场计算难度大，为了能够更精准地捕捉边界层梯度变化，对流体计算域的网格划分使用在壁面处划分边界层网格，在流体其他区域划分四面体网格的方法，可以有效的减少网格数量，并保證边界层处的计算精度。

通过对流体域进行不同密度的网格划分并进行数值模拟，将不同网格密度的模拟结果进行对比，发现在全局尺寸小于0.5 mm2，边界层数大于5层后，模拟结果受网格的影响较小。结合计算精度及计算机资源因素，设置全局最大尺寸为0.5 mm2。打开Sizing中的Capture Curvature对模型中存在曲率部位进行网格加密，并设置曲率法向角度为12°。打开Proximity对模型中狭窄区域进行加密，并设置间隙截面单元数量为4。在壁面处设置边界层网格，网格生成方法为Smooth Transition，设置层数为6层，增长率为1.2，网格生长方式为Pre，即先生成边界层网格，之后再生成四面体网格。最后点击Generate Mesh生成网格。

2.2边界条件与参数设定

选用三维双精度版本启动Fluent软件，在Fluent中选择基于压力的求解器，设为定常流动。由于本文所使用的模型复杂，气体为黏性可压缩气体，选择RNG k-ε湍流模型可在复杂的几何中产生更少的黏性流动，从而使模拟得到的流动状态更为精确。入口设为压力入口，压力为506 625 Pa，温度为520 K，湍流强度为10%，水力直径为12 mm。出口设为压力出口，压力为101 325 Pa，温度为450 K，回流湍流强度为10 %。其余设定为无滑移壁面边界，材料为steel。计算收敛残差标准设为1×10-5。

3结果与分析

在Fluent中计算完毕后，将计算结果导入后处理软件CFD-Post中进行后处理，得到熔喷双槽形喷嘴内部通道气体流场的速度及温度分布云图。为探究通气孔A及通气孔B在幅宽方向上的速度及温度分布均匀程度，选取通气孔A及通气孔B出口处的速度峰值及温度谷值为参数进行分析研究。

3.1熔喷双槽形喷嘴内部通道气体流场模拟结果

图7为通气孔A中心面的速度分布云图，从图7中可以看出气体在气腔1 中流动，依次进入通气孔A1、A2、A3及A4，且气体在通气孔A1至A4中的速度大小均不相同，其中通气孔A1中的气体速度最大，通气孔A4中的气体速度最小。这是由于气体在气腔1中流动时，气体依次被分配到通气孔A1、A2、A3及A4中，随着气体越往气腔中部走，气体速度越小，密度也越小，进入气孔中气体的初始速度和密度越来越小，从而導致了经气孔加速后的气体速度仍然较小。

图8为通气孔A中心面的温度分布云图，由于本文简化了流体与壁面的热量关系，将壁面设成了绝热壁面，因而在喷嘴内部通道中气体温度的变化仅与速度的变化有关。从图8中可以看出，气腔1中的气体温度呈两侧低中部高的趋势，通气孔A中气体温度的分布也为两侧气孔温度低，中部气孔温度高。根据对这一阶段气体速度分布云图的分析，气体在入口处速度较大，越往气腔1中部走，速度越小，温度随着速度减小而有所增高，这样的变化符合能量守恒定律。同样的，在通气孔A中，越靠近气腔外侧的气孔速度越大，越靠近气腔中部的气孔速度越小，因此通气孔A中的温度分布状况为两侧气孔温度低，越靠近气腔中部，气孔温度越高。

图9为通气孔B的速度分布云图，气体从通气孔A流出后，进入气腔2，再由气腔2进入通气孔B，由于通气孔B的截面积较通气孔A小，故气体在通气孔B中进行了第二次加速。在此对这15个圆孔从左往右依次编号为通气孔B1至通气孔B15。由于气体在通气孔A中完成加速后，通气孔A1至A4出口处的速度峰值各不相同，因此流入通气孔B各圆孔的初始速度存在差异。且在通气孔A中，各气孔的孔径大小不一，相邻气孔的孔距都各不相等，这些因素导致了气体在通气孔B中的气体分配问题。在经过通气孔B对气体的加速后，通气孔B各圆孔出口处的速度依然存在不匀，且整体上来看，靠近喷嘴外侧的圆孔出口处的速度较大，靠近喷嘴中部的圆孔出口处的速度较小，这是由上一加速过程的气体速度差异导致的。

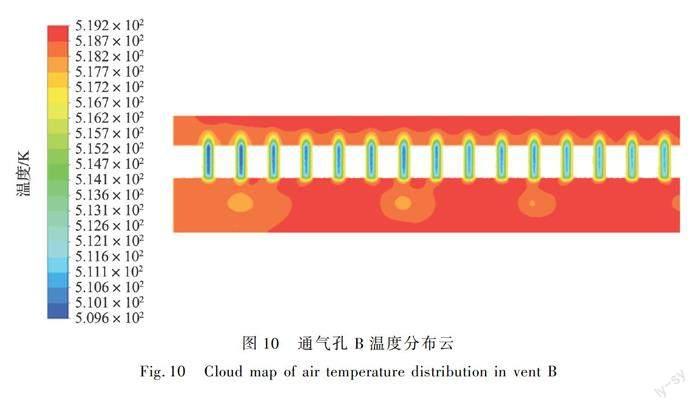
图10为通气孔B中的温度分布云图。由图10中可以看出，气腔2中的温度在从通气孔A1至A4中流出气体的主要流动路径上有所降低，在远离流动路径的区域温度变化不大，这是由于在主要流动路径上的气体速度较大，根据能量守恒定律，温度降低，而在远离流动路径的区域，由于速度变化较小，且在绝热条件下，气体没有与外界进行热量交换，因而温度几乎没有衰减。在气体进入通气孔B后，通气孔B中的温度整体都有所降低，且通气孔B1至B15中温度变化程度各不相同，整体呈两侧圆孔温度低于中部圆孔温度的趋势，这是因为通气孔B两侧圆孔的速度要高于中部圆孔的速度，因而温度的分布为两侧圆孔的温度较低，中部圆孔的温度较高。在气体流出通气孔B进入梯形气腔后，梯形气腔的截面积大于通气孔B的截面积，气体进入梯形气腔后不再加速，且有较小的衰减，这导致了梯形气腔中的温度有轻微的回升。

3.2通气孔A出口处气体速度与温度分析

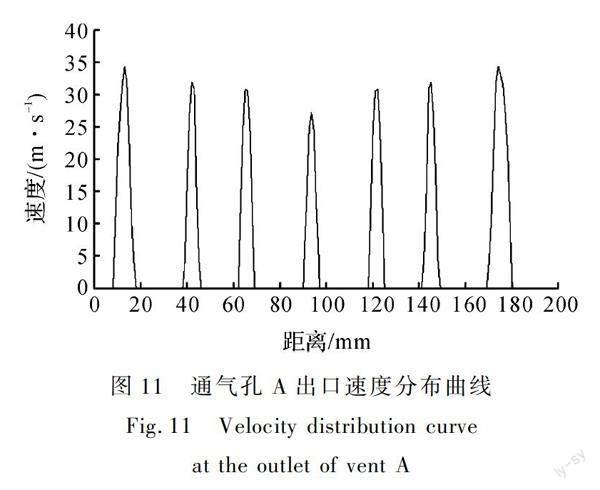
图11和图12分别为通气孔A出口处的速度分布曲线图和温度分布曲线图。从图11中可以看出气体经通气孔A加速后各气孔出口处的速度分布情况，其中，通气孔A1出口处的速度最大，达到34.4 m/s，通气孔A4出口处的速度最小，为27.3 m/s，通气孔A2与A3的速度分别为31.9、30.9 m/s，各气孔出口处的速度峰值均不相等，且最大速度峰值与最小速度峰值相差了7.1 m/s，差值为最小速度峰值（27.3 m/s）的26%，因而在通气孔A1至A4中速度分布有着明显的不均匀现象。气体速度在每个气孔中的分布趋势均为靠近壁面处速度极小，随着远离

壁面，速度逐渐增大，这是因为气体在气孔中流动时，由于边界层的存在，靠近壁面的气体在黏性的作用下几乎是层流状态，因而速度变得很小，而在远离边界的区域，气体的流动几乎不受黏性的影响，故速度逐渐增大。从图12可以看出通气孔A1至A4出口处的温度分布趋势正好与速度分布相反，通气孔A1出口处的温度最低，通气孔A4出口处的温度最高，两者的变化趋势符合能量守恒定律。虽然通气孔A的温度分布整体呈中部气孔高两侧气孔低的趋势，但最大值与最小值的差值并不大，这是因为这一阶段中整体速度较小，温度的变化仅由速度引起，因而温度各气孔出口处温度的差异并不大。

3.3通气孔B出口处气体速度与温度分析

图13为通气孔B的速度分布曲线图，图14为通气孔B的温度分布曲线图。从图13可以看出，通气孔B1至B1515个圆孔出口处的速度峰值均不相等，其中，通气孔B1出口处的速度峰值最大，达到54.9 m/s，通气孔B14出口处的速度峰值最小，为45.4 m/s，其余13个圆孔出口处的速度居于45.4 m/s至54.9 m/s之间，且各不相等。最大速度峰值与最小速度峰值相差了9.5 m/s，且差值为最小速度峰值（45.4 m/s）的21%，即经气孔组B加速后的气体依然存在着明显的速度分布不匀现象。在对速度分布云图进行分析的时候提到过，该阶段的速度分布不匀主要是由上一加速阶段，即通气孔A处的速度分布不匀导致的，进入通气孔B1至B15的气体由通气孔A1至A4分别提供，由于通气孔B的15个圆孔与通气孔A各气孔的距离各不相同，因此距离通气孔A近的圆孔获得的气体速度大，距离通气孔A远的气孔获得的气体速度小，从而导致了通气孔B1至B15出口处速度大小各不相同的现象。从图14可以看出通气孔B出口处的温度分布情况，可以发现，通气孔B1至B15出口处的温度大小各不相同，且整体分布趋势与速度分布趋势相反，该变化趋势符合能量守恒定律。这一阶段的速度虽较上一阶段有所增大，但整体速度仍然不高，故温度的变化仍然较小，由此也可以发现，仅因速度变化引起的温度变化是有限的，因此在后续的优化工作中，可以考虑将提升速度均匀性作为主要优化目标。

综上所述，发现通气孔B出口处的速度分布及温度分布与通气孔A的分布趋势相同，均为沿幅宽方向两侧气体速度高、温度低，中间气体速度低、温度高。因此可以判定，喷嘴内部通道中气流分布的不均匀性是由通气孔A中气流分布的不均匀性引起的，且对整个内部通道气体流场的分布有影响。在幅宽方向上，速度有明显的分布不匀，而温度的分布不匀程度较小，在熔喷法制备纤维中，拉伸聚合物熔体的气流速度和温度对纤维直径都有重要影响，因此气流速度的分布不匀会导致不同喷嘴位置拉伸出的纤维直径产生差异。

4结论

本文对熔喷双槽形喷嘴内部通道气体流场的三维模型进行了数值模拟，探究了喷嘴内部通道中气体速度和温度的分布状况，得到了以下结论：

a）气体在通气孔A1至A4出口处的速度峰值及温度谷值有所差异，分布趋势为越靠近气腔1外侧的通气孔出口处的速度峰值越大、温度谷值越小，越靠近气腔1中部的通气孔出口处的速度峰值越小、温度谷值越大。其中温度谷值的差异不大，而速度峰值差异明显，最大速度峰值与最小速度峰值相差了7.1 m/s，差值为最小速度峰值（27.3 m/s）的26%。

b） 通气孔B出口处的速度峰值及温度谷值的分布趋势大体上与通气孔A的分布趋势相同，且温度谷值的差异较小，而速度峰值差异明显，最大速度峰值与最小速度峰值相差9.5 m/s，差值为最小速度峰值（45.4 m/s）的21%。

c）通氣孔B出口处的速度峰值及温度谷值的差异由通气孔A出口处的差异导致，且通气孔A及通气孔B出口处的分布不匀主要表现为速度不匀。

参考文献：

［1］HARPHAM A S， SHAMBAUGH R L. Flow field of prac-tical dual rectangular jets［J］. Industrial and Engineering Chemistry Research， 1996， 35（10）： 3776-3779.

［2］HARPHAM A S， SHAMBAUGH R L. Velocity and tempe-rature fields of dual rectangular jets［J］. Industrial and Engineering Chemistry Research， 1997， 36（9）： 3939-3943.

［3］TATE B， SHAMBAUGH R L. Modified dual rectangular jets for fiber production［J］. Industrial and Engineering Chemistry Research， 1998， 37（9）： 3772-3779.

［4］KRUTKA H M， SHAMBAUGH R L. Analysis of a melt-blowing die： Comparison of cfd and experiments［J］. Industrial and Engineering Chemistry Research， 2002， 41（20）： 5125-5138.

［5］陈廷，黄秀宝.熔喷双槽形喷嘴气体射流流场研究［J］.中国纺织大学学报，2000，26（5）：28-32.

CHEN Ting， HUANG Xiubao. Study on gas jet flow field of melt blowing dual slot die［J］. Journal of China Textile University， 2000， 26（5）： 28-32.

［6］陈廷.熔喷非织造气流拉伸工艺研究［D］.上海：东华大学，2003：58-102.

CHEN Ting. Study on the Air Drawing in Melt Blowing Nonwoven Process［D］. Shanghai： Donghua University， 2003： 58-102.

［7］XIN S， WANG X. Investigation into the effect of the angle of dual slots on an air flow field in melt blowing via numerical simulation［J］. E-Polymers， 2016， 16（4）： 337-342.

［8］XIE S， HAN W. Turbulent air flow field in slot-die melt blowing for manufacturing microfibrous nonwoven materials［J］. Journal of Materials Science，2018，53（9）：6991-7003.

［9］姬长春，张开源，王玉栋，等.熔喷三维气流场的数值计算与分析［J］.纺织学报，2019，40（8）：175-180.

JI Changchun， ZHANG Kaiyuan， WANG Yudong， et al. Numerical calculation and analysis of three-dimensional flow field in melt-blown process［J］. Journal of Textile Research， 2019， 40（8）： 175-180.

［10］周梓豪，吴丽莉，陈廷.气相沉积法制备碳纳米管纤维反应器气体流场模拟［J］.现代纺织技术，2022，30（2）：99-105.

ZHOU Zihao， WU Lili， CHEN Ting. Simulation of gas flow field in reactor for preparation of carbon nanotube fibers by chemical vapor deposition［J］. Advanced Textile Technology， 2022， 30（2）： 99-105.

［11］刘宏霞，徐佳雯，陈廷.气相沉积法反应器内碳纳米管纤维运动模拟［J］.现代纺织技术，2022，30（2）：106-112.

LIU Hongxia， XU Jiawen， CHEN Ting. Motion simulation of carbon nanotube fibers in a vapor deposition reactor［J］. Advanced Textile Technology， 2022， 30（2）： 106-112.

Numerical simulation of air flow field in the inner passage of melt blowing dual slot die

JIANG Yingying， CHEN Ting

（College of Textile and Clothing Engineering， Soochow University， Suzhou 215021， China）

Abstract： Melt blowing is one of the main methods for preparing superfine fibers. The melt blowing method uses a high-speed and high-temperature airflow to draw polymer melt into superfine fibers. Therefore， the velocity and temperature of the drawing airflow have a key impact on the fiber diameter. Affected by the structure of the air flow passage inside the melt blowing nozzle， the velocity and temperature distribution of the air flow in the width direction of the nozzle have a certain degree of inhomogeneity， which leads to a certain difference in the diameter of the fibers produced at different positions of the nozzle.

In order to explore the influence of the passage structure inside the nozzle on the uniformity of the air velocity distribution， the air flow field in the inner passage of the melt blowing dual slot die was modeled. In the SpaceClaim module of the ANSYS Workbench platform， the establishment of the 3D geometric model of the air flow field and the extraction of the fluid computational domain were completed. Using ANSYS Mesh software， the fluid domain was meshed to meet the quality requirements and computational accuracy. The computational fluid dynamics software Fluent was used to numerically simulate the air flow field in the inner passage of the melt blowing dual slot die， and the velocity distribution and temperature distribution of the air in the inner passage of the nozzle were obtained. The results show that when the air flows from the air cavity 1 into the air hole group A， the maximum velocities at the exits of the vent holes A1 to A4 are significantly different. Specifically， the closer to the outside of the nozzle， the larger the maximum velocity is， and the closer the vent outlet is to the middle of the nozzle， the smaller the maximum velocity is. Among them， the velocity at the outlet of vent A1 is the largest， reaching 34.4 m/s， and the speed at the outlet of vent A4 is the smallest， at 27.3 m/s. The difference between the peak velocities of the two is 7.1 m/s， and the difference is 26% of the minimum velocity peak （27.3 m/s）. The temperature distribution trend at the exit of stomata A1 to A4 is exactly the opposite of the velocity distribution， the temperature at the outlet of vent A1 is the lowest， and the temperature at the outlet of vent A4 is the highest， and the trend of the two is in line with the law of conservation of energy. Similarly， the peak velocities at the exit of vent B1 to B15 are not equal. Specifically， the peak velocity at the outlet of vent B1 is the largest， reaching 54.9 m/s， and the peak velocity at the outlet of vent B14 is the smallest， being 45.4 m/s. The peak velocity difference between the two is 9.5 m/s， and the difference is 21% of the minimum velocity peak （45.4 m/s）. That is， there is still obvious uneven velocity distribution of the gas after acceleration by stomatal group B.

To sum up， we model and numerically simulate the air flow field in the inner passage of the melt blowing dual slot die， and explore the influence of the inner passage structure of the nozzle on the air velocity and temperature distribution. It provides some theoretical support for the optimal design of the internal channel of melt blowing dual slot dies and improvement of the uniformity of fiber fineness.

Keywords： melt blowing dual slot die; air flow field; inner passage; numerical simulation

收稿日期：20220317網络出版日期：20220530

基金项目：国家自然科学基金项目（51303121）；中国纺织工业联合会科技计划项目（2021036）

作者简介：姜莹莹（1996—），甘肃通渭人，女，硕士研究生，主要从事产业用纤维制品制备技术方面的研究。

通信作者：陈廷，E-mail： tingchen@suda.edu.cn