基于偏序关系确定特殊元素的标记方法

李晓阳

（太原理工大学软件学院，山西晋中 030600）

0.引言

依据偏序关系画哈斯图并求解特殊元素是离散数学课程考试中经常出现的一类问题，但是由于教材中的定义简洁凝练，相似度高，同学们很容易混淆[1]。本文在不偏离教材定义的基础上采用可视化的方法求解偏序关系中八大特殊元素。

1.相关概念

定义：设R 为非空集合A 上的关系。如果R 是自反的、反对称的和传递的，则称R 为A 上的偏序关系，记作≤。设≤为偏序关系，如果∈≤，则记作x≤y,读作x“小于或等于”y。

定义：设为偏序集，B ⊆A，y∈A。

（1）若∀x(x∈B →x≤y)成立，则称y为B 的上界。

（2）若∀x(x∈B →y≤x)成立，则称y为B 的下界。

（3）令C={y|y为B 的上界}，则称C 的最小元为B的最小上界或上确界。

（4）令D={y|y为B 的下界}，则称D 的最大元为B的最小上界或上确界。

定义：设为偏序集，B ⊆A，y∈B。

（1）若∀x(x∈B →x≤y)成立，则称y为B 的最大元。

（2）若∀x(x∈B →y≤x)成立，则称y为B 的最小元。

（3）若∀x(x∈B ∧y≤x→x=y)成立，则称y为B的极大元。

（4）若∀x(x∈B ∧x≤y→x=y)成立，则称y为B的极小元[2]。

2.基于偏序关系确定特殊元素的标记方法

2.1 确定哈斯图的标记方法

步骤一：在偏序关系二元表中标记相应的偏序关系。

步骤二：在偏序关系二元表中找行组中具有唯一标记的元素，该元素即为同一层元素。

步骤三：删除上一步骤中元素的列，在剩余元素中的行组找唯一标记的元素，该元素即为下一层元素。依据两层元素之间的偏序关系连线。

步骤四：重复步骤三。

2.2 确定八大特殊元的标记方法

子集B 上界确定方法：在集合B 中所有元素用不同的标志标记，每种标志逆流而上，并做出相同标志的标记，最终被集合B 中所有标志标记的元素即为上界。

子集B 下界确定方法：在集合B 中所有元素用不同的标志标记，每种标志顺流而下，并做出相同标志的标记，最终被集合B 中所有标志标记的元素即为下界。

子集B 上确界（最小上界）确定方法：先由标记法确定子集B 上界，若位于最下层的上界元素存在且仅存在唯一一个，则该元素即为上确界。

子集B 下确界（最大下界）确定方法：先由标记法确定子集B 下界，若位于最上层的下界元素存在且仅存在唯一一个，则该元素即为下确界。

子集B 极大元确定方法：在集合B 中所有元素用不同的标志标记，然后每种标志在集合B 中逆流而上，并做出相同标志的标记，最终流到尽头的元素即为极大元。

子集B2 最大元确定方法：若极大元被集合B 中所有标志标记，则该元素为最大元。

子集B 极小元确定方法：在集合B 中所有元素用不同的标志标记，然后每种标志在集合B 中顺流而下，并做出相同标志的标记，最终流到尽头的元素即为极小元。

子集B 最小元确定方法：若极小元被集合B 中所有标志标记，则该元素为最小元。

3.证明基于偏序关系确定特殊元素的标记方法

3.1 证明确定哈斯图的标记方法

哈斯图的标记方法采用递归的形式，先找出最上层元素，之后每找出一层的元素就与上一层元素之间依据偏序关系连线。

因为偏序关系具有自反性，在偏序关系二元表中每行至少有一个元素被标记（若被标记的元素唯一，即为自身元素），每行唯一被标记的元素说明该元素不与其他元素存在覆盖关系，则该元素在最上层。

根据递归方法，每次找出的元素均不与剩下的元素之间存在覆盖关系，则每次找出的元素唯一哈斯图的同一层，每两层元素之间依据偏序关系连线，最终哈斯图迎刃而解。

3.2 证明确定八大特殊元的标记方法

由标记范围确定原始定义中的y∈A 或y∈B。当y∈A 时，标记沿着整个哈斯图进行；当y∈B 时，标记范围仅限于子集中。

标记的方向确定原始定义中的x≤y或y≤x。当x≤y时，x对y有偏序关系，由覆盖关系确定标记方向为顺流而下；当y≤x时，y对x有偏序关系，由覆盖关系确定标记方向为逆流而上。

最小元是子集中的最小元素，它与子集中的其他元素都可比。最大元是子集中的最大元素，它与子集中的其他元素都可比。“都可比”使用被子集中所有元素的标志标记来表示。

上确界与下确界中的“最大”与“最小”通过元素的上下层的关系来体现。

4.方法示例

例如，画出偏序集的哈斯图，找出A 的子集B 的极大元、极小元、最大元、最小元、上界、下界、上确界和下确界[3]。

A=P({a,b,c}),≤={|x∈P(A)∧y ∈P(A)∧x⊆y},B={∅,{a},{b},{a,c}}

解法：集合A={∅,{a},{b},{c},{a,b},{a,c},{b,c},{a,b,c}}。

R={<∅，∅>,<∅，a>,<∅，b>,<∅，c>,<∅，{a,b}>,<∅,{a,c}>,<∅,{b,c}>,<∅,{a,b,c}>,,,,,,,,,,,,,<{a,b},{a,b}>,<{a,b},{a,b,c}>,<{b,c},{b,c}>,<{b,c},{a,b,c}>,<{a,c},{a,c}>,<{a,c},{a,b,c}>,<{a,b,c},{a,b,c}>}

步骤一：在偏序关系二元表中标记相应的偏序关系。偏序关系二元表执行步骤一如表1 所示。

步骤二：在偏序关系二元表中找行组中具有唯一标记的元素，集合{a,b,c}即为最上层元素。执行步骤二中确定元素结果如表2 所示，所画哈斯图（部分）如图1 所示。图1 确定哈斯图的标记方法步骤二执行结果。

图1 确定哈斯图的标记方法步骤二执行结果

表2 偏序关系二元表执行步骤二结果

步骤三：删除上一步骤中元素的列，在剩余元素中的行组找唯一标记的元素，该元素即为下一层元素。依据两层元素之间的偏序关系连线。执行步骤三中确定元素结果如表3 所示，所画哈斯图（部分）如图2 所示。

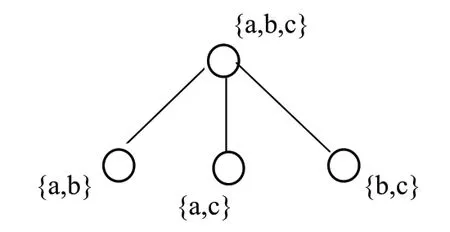
图2 确定哈斯图的标记方法步骤三执行结果

表3 偏序关系二元表执行步骤三结果

步骤四：删除上一步骤中元素的列，在剩余元素中的行组找唯一标记的元素，该元素即为下一层元素。依据两层元素之间的偏序关系连线。执行步骤四中确定元素结果如表4 所示，所画哈斯图（部分）如图3 所示。

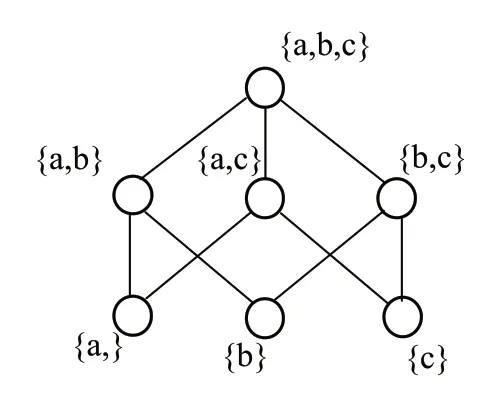
图3 确定哈斯图的标记方法步骤四执行结果

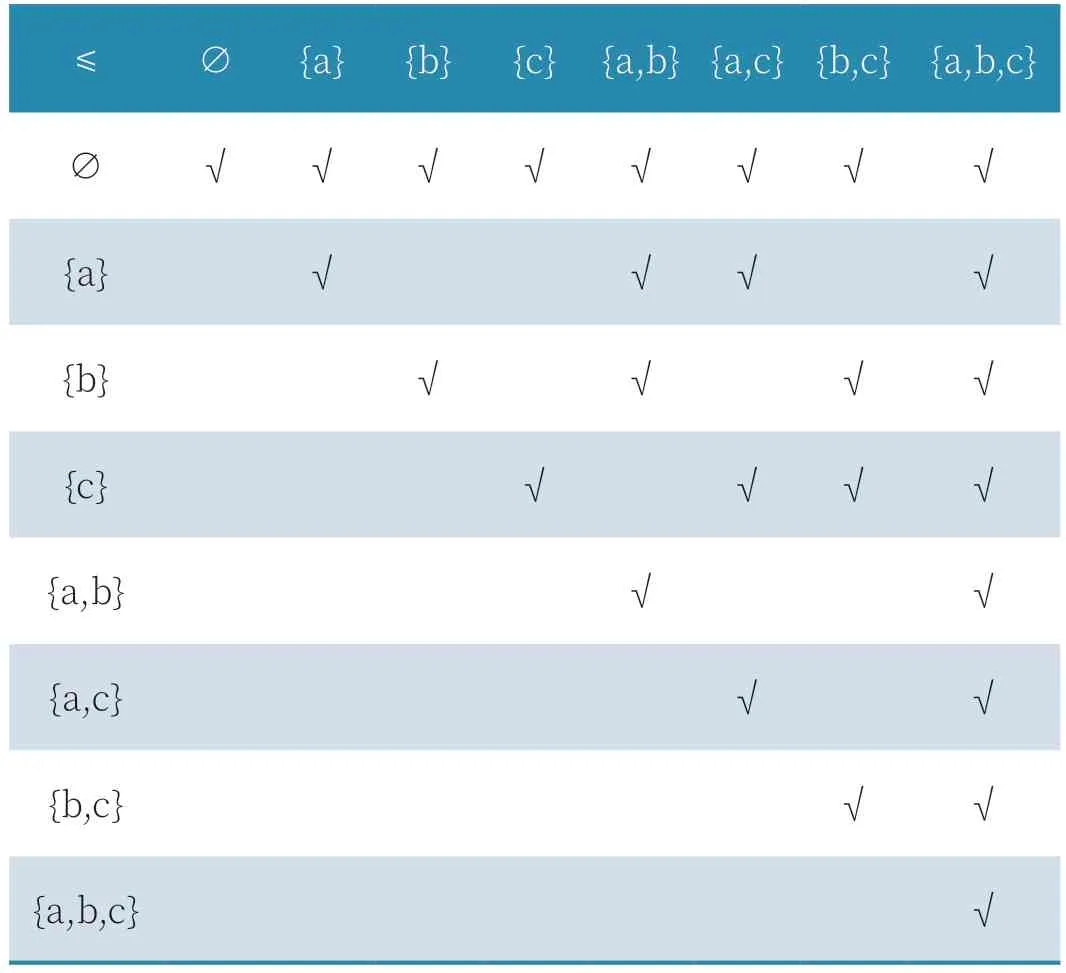
表4 偏序关系二元表执行步骤四结果

步骤五：删除上一步骤中元素的列，在剩余元素中的行组找唯一标记的元素，该元素即为下一层元素。依据两层元素之间的偏序关系连线。执行步骤五中确定元素结果如表5 所示，所画哈斯图（部分）如图4 所示。

图4 确定哈斯图的标记方法步骤五执行结果

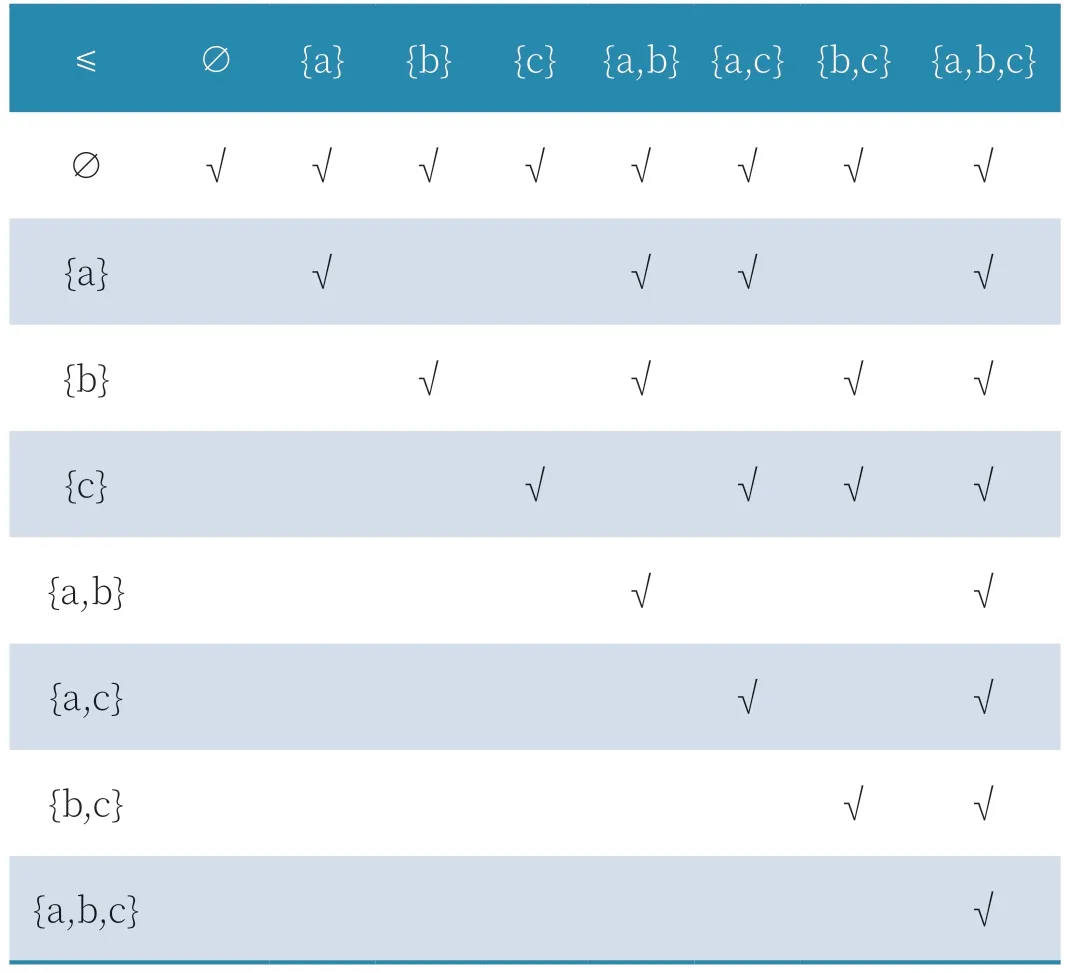
表5 偏序关系二元表执行步骤五结果

为使确定偏序关系八大特殊元的标记方法更清晰地表现，确定子集B 的标记方法分别如图5 ～图8 所示。

图5 确定子集B上界和上确界的标记方法

图6 确定子集B下界和下确界的标记方法

图7 确定子集B极大元、最大元的标记方法

图8 确定子集B极小元、最小元的标记方法

子集B 上界确定方法: 在集合B 中分别将元素{∅}、{a}、{b}、{a,c}标记为●、▲、◆、★。然后每种标志沿哈斯图逆流而上，并做出相同标志的标记，最终被集合B中所有标志标记的元素{a,b,c}即为上界。

子集B 上确界（最小上界）确定方法：位于最下层的上界元素存在且仅存在唯一一个，则{a,b,c}为上确界。

子集B 下界确定方法: 在集合B 中分别将元素{∅}、{a}、{b}、{a,c}标记为●、▲、◆、★。然后每种标志沿哈斯图顺流而下，并做出相同标志的标记，最终被集合B中所有标志标记的元素{∅}即为下界。

子集B 下确界（最大上界）确定方法：位于最上层的下界元素存在且仅存在唯一一个，则{∅}为下确界。

子集B 极大元确定方法：在集合B 中分别将元素{∅}、{a}、{b}、{a,c}标记为●、▲、◆、★。然后每种标志在集合B 中逆流而上，并做出相同标志的标记，最终流到尽头的元素{a,c}和{b}即为极大元。

子集B 最大元确定方法：若极大元被集合B 中所有标志标记，则该元素为最大元。子集B 无最大元。

子集B 极小元确定方法: 在集合B 中分别将元素{∅}、{a}、{b}、{a,c}标记为●、▲、◆、★。然后每种标志在集合B 中顺流而下，并做出相同标志的标记，最终流到尽头的元素{∅}即为极小元。

子集B 最小元确定方法：若极小元被集合B 中所有标志标记，则该元素为最小元。子集B 最小元为{∅}。

方法示例结果集如表6 所示。

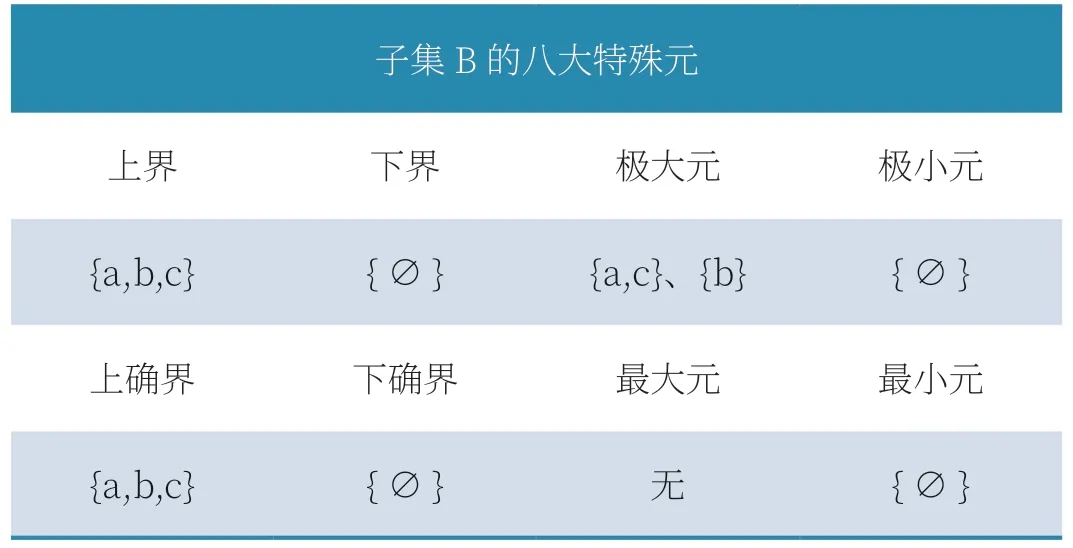
表6 方法示例结果集

5.研究意义

基于哈斯图确定偏序关系八大特殊元的标记方法可以将原依据定义的确定方法简便化，在拓展到更大的集合与子集中更具有优势。此外，在同学们学习《离散数学》课程中通过标记方法更能将定义可视化，有助于抽象化的理解。