提升推理能力 发展数学素养
林森

[摘 要] 在初中数学教学中应开展直击课程本质的“深度教学”,以此让学生学会思考、学会探索、学会发现、学会学习. 文章以问题为主线,引导学生通过类比确定研究新知的基本方法和基本路径,另外借助不同问题引发学生进行深度思考,以此深化知识理解,有效提高学生的推理能力,促进“教”与“学”的全面提升.
[关键词] 深度教学;深度思考;推理能力
推理是学生学习数学常用的思维方式,是学生学好数学的前提和保障. 在数学课堂上要重视学生推理能力的发展和提升,使其成为提升学生数学学习能力的“助推器”和落实学生核心素养的“稳压器”. 在初中数学教学中,大多教师也很关注学生推理能力的发展,只不过发展学生推理能力的主要途径是“刷题”,从短期效果来看,学生可以通过模仿、复制的方法解决一些相似的问题,但从长远发展来看,学生的思维方式和学习能力并没有得到“质”的提升. 为了改变这一现状,在数学教学中应实施“深度教学”,教学中不要局限于单一知识的讲解、单一问题的解决,应从整体和全局的角度去思考问题,建构认知体系,引导学生从特殊中抽象出一般数学思维和策略,这样学生不再是数学教学的盲从者,而是高质课堂的建设者,以此提高学习积极性,提升思维品质[1].
教学“直角三角形斜边中线的性质”时,笔者以学生已有认知为出发点,借助层层递进的问题来诱发学生深度思考,提升教学品质.
教学分析
本章节教学目标是在研究图形性质和运动过程中,发展学生的空间观念. 学习本节课前,学生已经掌握了等腰三角形的相关性质和判断定理,以及研究几何图形的基本方法,这为本节课开展自主探究活动提供了知识储备和方法保障. 教学中教师要改变“以教为主”的教学方式,通过创设不同问题来调動学生应用已有知识和已有经验,用“联系类比”和“问题引领”的方式让学生学会探索、学会发现、学会抽象,发展学生推理能力[2].
教学设计
1. 回顾思考
师:等腰三角形是什么图形呢?
生齐声答:轴对称图形.
师:很好,现在我们结合下面两个问题回顾一下研究等腰三角形的基本方法,得到了哪些结论. (教师用PPT给出问题)
问题1:说一说等腰三角形的性质定理和判定定理分别是什么.
问题2:回顾一下研究性质定理的主要步骤是什么,研究方法是什么.
对于问题1,其涉及的内容在课堂教学中重点研究过,在练习中灵活应用过,教师也让学生熟练记忆过,因此学生很快就给出了准确的答案. 对于问题2,教师引导学生结合教材内容进行沟通交流,一致认为研究定理主要经历了四个步骤,分别是操作、探究、归纳、证明. 研究方法:通过动手操作(折叠),引导学生观察顶角平分线、底边上的中线、底边上的高线的关系,从而引发数学猜想;接下来通过合情推理和演绎推理相结合的方式进行推理验证,得到了等腰三角形的性质定理;同时又构造逆命题,运用演绎推理进行验证,得到了等腰三角形的判定定理.
设计意图 在问题的引领下,引导学生回顾具体知识的研究方法,从而推广为研究几何图形的基本方法,强化了学生对方法策略的认识,为研究新的几何图形做好了铺垫. 同时在教学中与旧知相关联,引导学生用“联系类比”的方法思考问题、分析问题,使学生的思维更具逻辑性,有助于学生认知体系的建构. 另外,借助“联系类比”更易于引发学生的情感共鸣,是“深度教学”的重要环节,更易于学生理解和接受.
2. 探索新知
环节1:合情推理,发现结论.
合情推理是基于已有认知水平的一种推理,其本质是利用已经验证过的知识或方法去推理和验证那些未验证过的知识和方法,体现了由特殊到一般的思维策略,展现了深度教学的一般过程.
师:通过刚刚的回顾,我们已经总结和归纳了研究几何图形的基本思想方法,今天我们就来应用它来研究直角三角形的斜边上的中线.
师:现在就利用我们课前准备的直角三角形,开启我们的探究之旅.
师:结合研究等腰三角形的基本方法,你认为我们的第一步应该做什么呢?
生1:动手操作. 先通过“折一折”得到中线,然后再“量一量”,看看它与哪条边存在什么样的数量关系.
师:很好,现在请大家动手做一做、看一看,猜想一下这条斜边中线会与哪条边存在一定的数量关系呢.
生2:折叠后感觉斜边的中线与斜边应该存在着数量关系.
师:很好,现在我们就动手“量一量”,看看有什么发现.
生3:经过测量我发现斜边的中线正好是斜边的一半.
师:现在我们不用折叠法了,通过画一画、量一量,看看能否得到相同的结论.
设计意图 合情推理是基于已有现实的一种推理,其本质是利用已经验证过的知识或方法去推理和验证那些未验证过的知识和方法,体现了由特殊到一般的思维策略,展现了深度教学的一般过程. 教学中教师引导学生通过“画”“折”“量”等操作活动,提出了猜想,并应用不同方法进行验证,培养了学生合情推理能力,同时又为后面的演绎推理做好了铺垫. 在折纸、测量等实践活动中,教师为学生提供了自由的、广阔的探索空间,引导学生通过折叠发现了蕴含其中的数学规律,让学生在“做”的过程中逐渐发现了数学本质,有利于发展学生的直觉思维,有助于培养学生的空间观念,发展学生的合情推理能力[3].
环节2:演绎推理,验证结论.
师:刚刚通过测量和折叠我们发现了直角三角形斜边上的中线与斜边的数量关系,接下来我们需要做什么呢?
生齐声答:验证.
师:很好,判断一个命题是否为真命题需要进一步验证,那么如何用已学过的知识进行证明呢?
师:根据以上结论,你认为其本质是证明什么?
生齐声答:线段相等.
师:那么有哪些方法可以证明线段相等呢?(教师预留时间让学生回顾、交流)
生4:等腰三角形中等角对等边.
生5:还可以利用全等三角形.
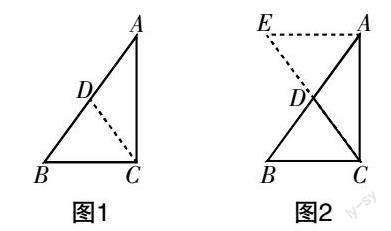
师:很好. 如图1所示,我们先尝试用生4的方法证明,看看这个方法是否行得通. (证明略)
师:如图2所示,你是否能通过生5的思路,利用“全等三角形”的思路证明以上结论成立?(证明略)
以上证明对于大多数学生来讲可谓轻车熟路,不过也有个别学生一时没有找到解题的突破口,教师鼓励学生进行互动交流,很快大家完成了证明. 证明结束后教师引导学生分别用文字语言和符号语言总结归纳出直角三角形斜边中线的性质定理,教师详细板书.
设计意图 在教学中,教师将证明过程拆分成了若干小问题,在问题的引领下从不同角度探索论证了结论. 这样将合情推理的探索活动与演绎推理的验证活动有机地结合在一起,体验了研究几何图形的基本方法,让學生知道证明是探索活动的自然延续,是必不可少的一环. 教学中教师并没有让学生急于证明,而是借助问题让学生理解问题的本质,即证明线段相等,这样巧妙地将证明性质转化为学生熟悉的证明线段相等的问题,这样从已有的知识、经验出发,为演绎推理提供了知识保障,符合演绎推理的特点. 通过前面问题的铺垫,学生给出了不同的证明线段相等的方法,接下来教师让学生运用不同的方法进行证明,这样既顺应了学生的思维发展,又丰富了学生的解题思路,为学生的全面发展创造了良好的契机. 同时,教学中教师改变了传统的灌输式教学,通过师生和生生互动交流的方式,引导学生自主构造恰当的辅助线,学生通过互动交流顺利地找到了问题的突破口,有效地提升了学生的演绎推理能力. 可见,“刷题”并不是提升学生演绎推理能力的唯一途径,还可以渗透于公式、定理的证明活动中. 这样以问题为导向,鼓励学生独立思考、合作交流,体现了深度教学的教学理念,提升了学生的数学学习能力. 同时,教学中教师鼓励学生应用不同的策略进行证明,通过对已有知识、经验的迁移和重组,不仅巩固了学生原认知,而且探索学习了新知,提升了学生的解题技能.
环节3:逆向推理,完善认知.
师:在学习等腰三角形时,学习了性质定理后,接下来研究的是什么问题呢?
生齐声答:判定定理.
师:很好,那么以上命题的逆命题应该是什么呢?
教师预留时间让学生思考,学生顺利地给出了逆命题.
师:这个逆命题是否成立呢?你能将逆命题转化为符号语言并证明吗?
生6:如图1所示,在△ABC中,AD=BD,BD=CD,求证:∠ACB=90°.
这样通过文字语言和符号语言的互化,深化了学生对逆命题的理解. 转化为符号语言后,问题更加直观,更易于学生理解,学生顺利地应用已有知识证明了给出的逆命题.
设计意图 在研究线段、角、等腰三角形等平面几何图形时,学习了性质定理后会对知识继续拓展,引导学生继续研究它的判定定理,以此深化理解,提升学生的演绎推理能力. 另外,经历命题的正逆互化有效地发展了学生逆向思维. 众所周知,数学知识是灵活多变的,有时候一个问题稍加改动就变成了另一个全新的问题,那么在面对这些灵活多变的问题时,学生难免会出现思维障碍,苦思冥想也不能获解,此时若从反面出发可能会有一些意外的收获. 从实践反馈来看,大多学生在思考和解决问题时主要依赖的是正向思维,学生的逆向思维意识淡薄,这就要求在平时教学中多关注逆向思维的发展. 如在证明了命题后,引导学生思考逆命题,这样不仅可以训练学生的逆向思维,而且可以有效提升学生的推理能力,有利于“深度教学”目标的达成.
这样在探索中,将命题与逆命题联系起来,学生的思维更加严谨,对性质定理的记忆更加深刻,有助于学生完成认知体系的建构. 在课堂教学中,教师应多为学生营造一些机会进行探索和验证,以此丰富深度教学的内容,助力学生推理能力的提升.
3. 应用新知
习题训练在数学课堂教学中是必不可少的一环,能起到深化知识的理解、巩固和内化的作用. 那么为了发挥习题训练的价值,教学中要少一些“就题论题”,应将知识和问题有机地结合在一起,注重培养思维的逻辑性和缜密性.
例1 如图3所示,在△ABC中,AD是高,E,F分别是AB,AC的中点,若AC=8,AB=10,求四边形AEDF的周长.
在解题前,教师没有让学生直接证明,而是给出了如下问题.
问题1:图3中你是否发现了本节课的新知呢?
问题2:根据本节课所学的内容,在Rt△ABD中,你能得到哪些线段间的数量关系?在Rt△ADC中,你又发现了什么?
例2 如图4所示,∠ABC=∠ADC=90°,M,N分别是AC,BC的中点. 求证:MN⊥BD.
同样,在解答例2前,教师先让学生思考如下问题.
问题1:如图4所示,你能找到直角三角形的斜边中线吗?如果找不到是否能够通过构造的方法得到呢?
问题2:运用本节课所学的定理,在Rt△ABC中,你能得到什么结论?在Rt△ADC中呢?
问题3:在图4中,除了Rt△ABC和Rt△ADC,还有其他的特殊三角形吗?
问题4:回顾特殊三角形的性质,可以得到哪些结论?
设计意图 例1较为简单,直接应用本节课所学的性质定理就能轻松地证明结论. 例2具有一定的综合性,既考查了本节课所学的内容,又考查了等腰三角形的性质. 在例2的证明过程中,教师没有直接给出辅助线,而且借助问题引导学生自己添加辅助线,继而得到“直角三角形斜边中线”的基本图形. 接下来又引导学生寻找其他特殊三角形,学生通过观察发现了等腰三角形,最后应用等腰三角形“三线合一”的性质解决了问题. 在应用环节,教师既通过问题为学生指引了方向,又提供了适宜的空间让学生独立思考,这样借助层叠的问题将相关知识有效地串联在了一起,让学生的思维更有逻辑性.
教学反思
无论是学习还是生活,推理都有着重要的应用,那么数学作为基础学科,要充分发挥其学科价值,关注学生推理能力的培养和提升. 教师要认识到,学生推理能力的提升是一个长期的过程,需要渗透于课堂教学中,并贯穿始终,进而通过潜移默化的引导促进学生全面发展,提高学生综合素养.
教学中教师借助不同的问题,诱发学生深度思考,引导学生通过观察、探索、分析、交流,找到解决问题的突破口,以此树立学生学习数学的信心. 此外,教学中教师应放手让学生去探索和验证,让学生真正地参与到课堂教学中来,充分展示学生的思维过程,巧妙地借助问题情境引导学生发现有价值的规律,体验数学发现之美.
总之,实际教学中教师应将培养学生推理能力的思想融于课堂教学,通过“由浅入深”的问题,引导学生深度思考,从而将知识和技能内化为能力,助力学生综合素质提升.
参考文献:
[1] 刘东升. 追求适合初中学生的教学深度[J]. 中学数学月刊,2014(09):20-25.
[2] 李其踊. 初中数学核心素养之推理能力培养[J]. 新课程(中学),2017(08):181.
[3] 汪祥艳. 基于数学核心素养的初中数学教学优化策略[J]. 数学学习与研究,2019(05):93.

