时序优先级约束的时序模式图强模拟匹配

金浩宇,霍 宏,方 涛

(上海交通大学 电子信息与电气工程学院,上海 200240)

0 引 言

图模式匹配是指在图数据中搜索与待查询模式图相同或相似的子图的一类算法,是实现图数据高效率查询的重要手段,已经应用于众多的领域。例如社交网络分析[1]、知识分析[2]等。现有的图模式匹配方法大多仅适用于静态图,不适用于在现实世界中广泛存在的时态图[3-4],即图数据中的两个顶点之间的边具有时间属性,其记录了两个顶点之间关系的开始与结束时间。图1(a)给出了一个任务合作时序图,图中每个顶点表示一个人,顶点标签A,B,C,D,E表示不同的职业,顶点之间的有向边表示两个人之间交接任务的方向,每条边上都有一个时间区间(s,f)表示任务交接的开始时间s与结束时间f。

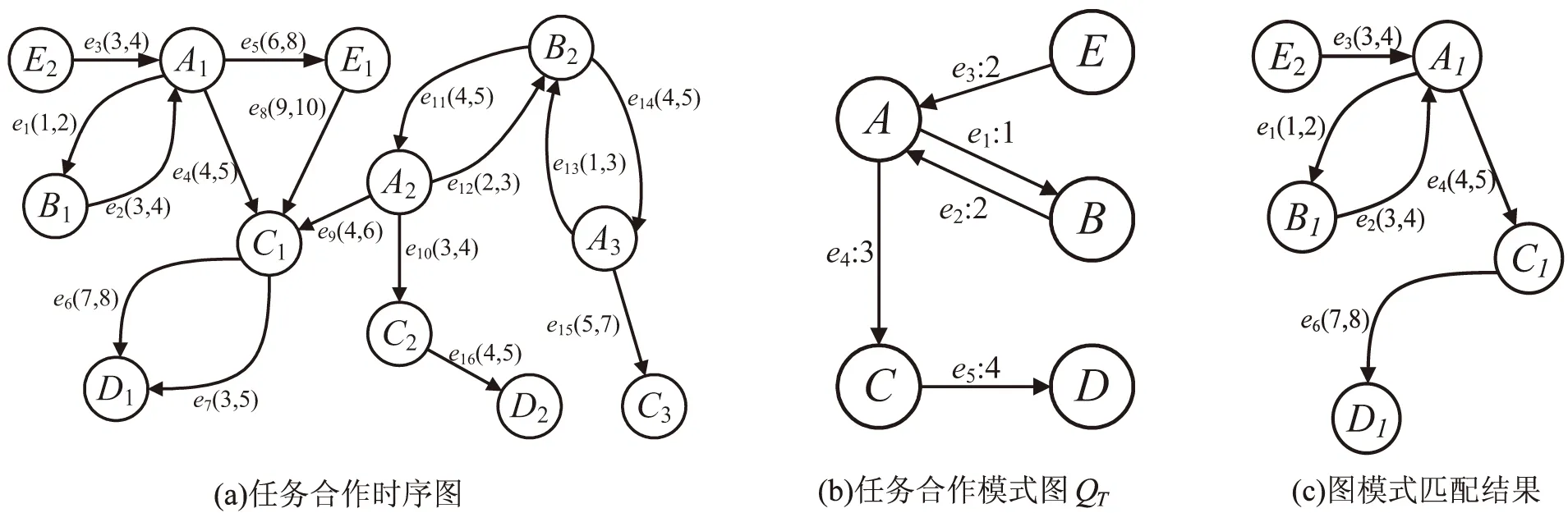
图1 任务合作时序图

假设有一个任务合作模式图QT,如图1(b)所示,QT中每条边ei都具有一个时序优先级,时序优先级规定了低优先级边的开始时间一定要晚于高优先级边的结束时间,即模式图QT隐含着一种时序约束,该文称其为时序模式图,其中A先与B交接任务,然后A在接收了B和E的交接信息后,再与C进行交接,最后C与D完成任务交接。现要在如图1(a)所示的任务合作时序图上查询与QT相同或相似的子图。如果采用静态的图模拟匹配方法,可以得到的一个匹配结果的边集合为{e1,e2,e3,e4,e6,e7},显然,由于没有考虑边具有的时序属性,边e7并不满足模式图QT中的时序约束,而正确的匹配结果如图1(c)所示。除了时序约束外,观察图1(b),不难发现模式图QT中还存在环路,如A→B→A等,而现有的时态图模式匹配方法无法处理模式图中的环路。因此,需要研究适合于时态图并能处理环路的时序模式图匹配方法。

针对时序图特有的时序属性兼顾其拓扑结构,提出了时序优先级约束的时序模式图强模拟匹配算法,该算法在匹配过程中,不仅对拓扑结构进行检查,还将各条边的时序优先级作为局部约束,并设置了冗余顶点过滤规则来缩小搜索范围,以及对时序检查的队列顺序进行优化使得算法能够提前剪枝,减少了计算复杂度,所提出的方法兼具子图同构和图模拟的优势,实现了既准确又高效的图匹配。在三个时序数据集上的大量实验表明,相比传统的强模拟算法,所提算法能够有效过滤错误结果,并且在不同规模的数据图上均具有良好的性能表现。

1 相关工作

1.1 近似匹配

近似匹配放松了图匹配条件,成为广泛采用的一种图模式匹配方法,主要包括图模拟[5]、双向模拟[6]、强模拟[7]、受限模拟[8]、量化模拟[9-10]等。图模拟要求匹配每个节点以及其子节点。双向模拟在图模拟的基础上还要匹配父节点。强模拟在双向模拟基础上还需考虑匹配子图的局部特性。受限模拟是指在模式图上对跳跃次数进行了限制。量化模拟关注了图上的具有计数量词的表达模式。上述的近似匹配方法都只考虑了图的拓扑结构,而忽略了图上的时间信息,无法用来解决在时态图上的匹配问题。

1.2 时态图及其图模式匹配

时态图主要用于对实体及其之间涉及的时态关系进行建模,是在静态图的基础上演变的一种新型图数据[11]。目前,关于时态图的研究主要包括可达性查询[12]、最小生成树[13]、最短时态路径[14]等。

时态图上的图模式匹配问题的研究才刚刚起步,Xu等[15]研究了时态图同构匹配,提出了时间约束的模式图匹配算法(Time-Constrained Graph Pattern Matching,TCGPM),但同构匹配要求匹配到与查询模式图完全相同的子图,过于严格。Song等[16]研究了图流上的事件模式匹配,将时间窗口概念引入了子图匹配并提出了DDST(Degree-Preserving Dual Simulation with Timing Constraints)算法,且基于标签过滤与度约束的思想提出了两个优化算法DDST-SIGNATURE和COLORING以提升算法的运行效率,但是这些算法将给定时间窗口的时态图快照作为静态图处理,容易导致遗漏部分结果。Ma等[17]根据受限模拟和时态路径定义了时态图上的图模式匹配并基于连接的方式枚举匹配结果,但是这种方法的匹配条件过于宽松,并且不允许模式图中出现环路。

2 模式图匹配与时序模式图匹配的形式化描述

双向模拟和强模拟是经典的模式图匹配算法,两者的形式化描述如下：

定义1 双向模拟。给定一个模式图Q=(Vq,Eq,Lq)和一个数据图G=(V,E,L),如果存在一个二元匹配关系S⊆Vq×V且满足下列条件,则说G通过双向模拟匹配Q：

(1)每一对(u,v)∈S,u和v都有相同的标签;

(2)对每个v∈Vq,存在u∈V满足(u,v)∈S且每一条边e'(v,v1)∈Eq都存在一条边e(u,u1)∈E使得(u1,v1)∈S;

(3)对每个v∈Vq,存在u∈V满足(u,v)∈S且每一条边e'(v2,v)∈Eq都存在一条边e(u2,u)∈E使得(u2,v2)∈S。

定义2 强模拟。给定一个模式图Q=(Vq,Eq,Lq)和一个数据图G=(V,E,L),若在G中存在一个顶点v和一个连通子图Gs(Vs,Es)满足以下条件,则说G通过强模拟匹配Q：

(1)Q对Gs满足双向模拟匹配,且有最大二元匹配关系S,即Q在G上的任意二元匹配关系SA都有SA⊆S。

(2)Gs是S构成的图,即(a)有一个顶点w∈Vs当且仅当它存在于S。(b)有一条边e(w,w')∈Es当且仅当在Q中存在一条边e'(u,u')使得(u,w)∈S且(u',w')∈S。

时态图的边具有时间属性,其形式化描述为：

定义3 时态图。给定一个有向带标签的图GT=(V,E,L),其中V是顶点的集合;E∈V×V是有向时态边的集合;L是一个标签函数,可将每个顶点u∈V映射到其对应的标签L(u)。假设图中一条有向时态边ei∈E连接了两个顶点u,v∈V,可表示为一个四元组(u,v,si,fi),该四元组的含义为两个顶点u和v的关系从时间点si开始到时间点fi结束。

时态图的模式图及其强模拟匹配算法的形式化描述如下：

定义4 时序模式图。一个时序模式图表示为QT=(Vq,Eq,Lq),其中Vq是顶点的集合,Lq是一个标签函数,Eq∈Vq×Vq是有向时序优先级边的集合。一条有向时序优先级边ei∈Eq可表示为一个三元组(u,v,pi),其中pi为ei的时序优先级。时序模式图不关心具体的时间范围,而是通过时序优先级规定每条边代表的事件发生的先后顺序,时序优先级低的事件必须在时序优先级高的事件结束之后发生。

定义5 时序强模拟匹配。给定一个时序模式图QT=(Vq,Eq,Lq)和一个时态数据图GT=(V,E,L),如果满足以下条件,则称G通过时序强模拟匹配QT：

3 文中算法

该文提出的时序优先级约束的时序模式图强模拟匹配算法(Temporal Priority Constrained Graph Pattern Strong Simulation Matching,TPC-GPSSM)针对时序图特有的时序特性,将各条边的时序优先级作为局部约束,在匹配过程中,能够同时兼顾时序图边具有的时序优先级及其拓扑结构,也适用于带环路的时序模式图的匹配。

3.1 TPC-GPSSM算法

TPC-GPSSM算法主要先在时态图上构建球,然后在球上进行时序优先级约束的强模拟匹配。在时态图上构建球采用广度优先遍历(Breath First Search,BFS)算法[18],以每个顶点为球心,构造半径为时序模式图直径的球,可将构建好的每个球看作是时态图的一个子图。然后,将每个球与时序模式图进行双向模拟匹配,在匹配过程中,一方面要计算每个球其所包含的二元匹配关系,并检查时序优先级约束,找到最大的二元匹配关系。另一方面,在匹配的同时还进行拓扑结构检查,以保证匹配的子图与时序模式图匹配。

算法1 TPC-GPSSM

输入：时序模式图QT=(Vq,Eq,Lq)及其直径dq,时态图GT=(V,E,L)

输出：匹配结果集合S

1.S：=∅,B：=∅

2.for eachvinVdo

6.sim(v),sim(e')：=TemporalFilter(QT,sim(v),sim(e'))

7.Gs：=CheckTopology(QT,sim(v),sim(e'))

8.ifGs≠∅ then

9.S：=S∪Gs

10.returnS

算法2 DualSimMatch

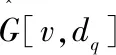
输出：候选顶点集合sim(v),候选边集合sim(e')

1.for eachv∈Vqdo

2.sim(v)：={u|uis inG[v,dq] andLq(u)}

3.for eache(v,v1)∈Eqdo

4.sim(e')：={e|e(u,u1)is inG[v,dq],u∈sim(v),u1∈sim(v1)}

5.while there are changes do

6. for eachu∈sim(v) do

7. for eache(v,v') inEqdo

9.Removeuand edges containingufrom sim(v) and sim(e')

10. for eache(v',v) inEqdo

12.Removeuand edges containingufrom sim(v) and sim(e')

13.return sim(v),sim(e')

算法3 TemporalFilter

输入：时序模式图QT,候选顶点集合sim(v),候选边集合sim(e')

输出：候选顶点集合sim(v),候选边集合sim(e')

1.while there are changes do

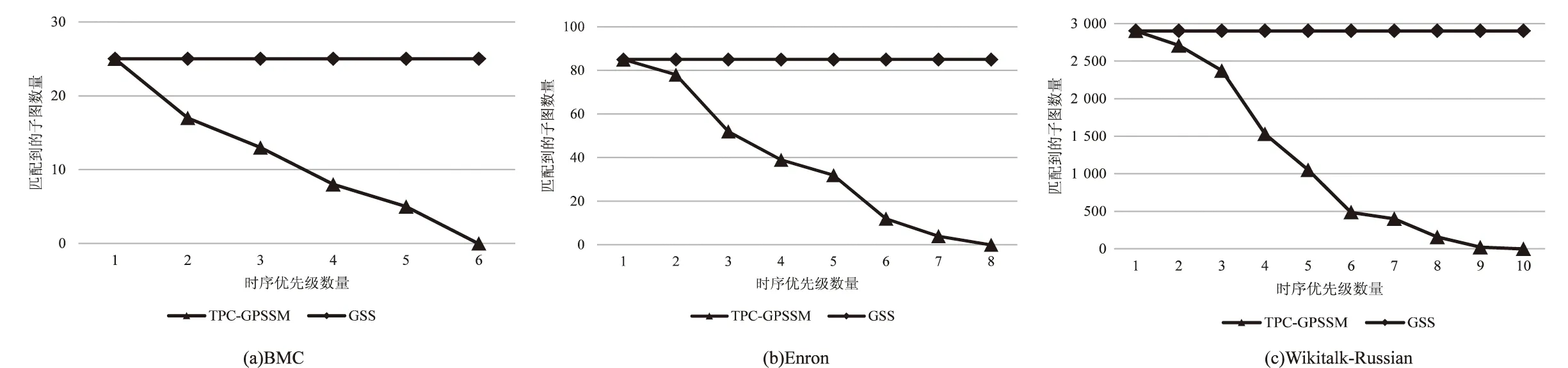
4. ifp1>p2ands1

7. Removeu,u1and all edges containingu,u1from sim(v) and sim(e')

8.return sim(v),sim(e')

算法4给出了拓扑结构检查的伪代码CheckTopology,主要功能是对球内的子图进行检查,去除在时序优先级约束下因删除时态边而产生的不符合QT拓扑结构要求的顶点和边。对顶点候选集sim(v)中的任意顶点u,首先检查其后继关系,后继顶点集合为succ(u),后继顶点候选集为sim(v'),若succ(u)∩sim(v')=∅,则将该节点及其关联的边从候选集合中删除;然后检查其前驱关系,前驱顶点集合为pred(u),前驱顶点候选集为sim(v''),若pred(u)∩sim(v'')=∅,则将相关顶点和边删除(见第1-5行)。若顶点和边候选集均非空,则将其构造成一个子图Gs(见第6-8行)。

算法4 CheckTopology

输入：时序模式图QT,候选顶点集合sim(v),候选边集合sim(e')

输出：匹配子图Gs

1.While there are changes do

2. for eachu∈sim(v) do

3. if succ(u)∩sim(v')=∅ or pred(u)∩sim(v'')=∅ then

4.sim(v)：=sim(v){u}

5.remove all edges containingufrom sim(e')

6.if sim(v),sim(e')≠∅ then

7. constructGsfrom sim(v),sim(e')

8.returnGs

TPC-GPSSM在球的建立过程花费了很多时间,主要因为每个球包含了很多无用的拓扑结构信息,并且在时序检查过程中存在重复检查的问题。如果能减少每个球的计算量, 避免时序的重复检查,将大大提升算法的效率。

3.2 TPC-GPSSM算法优化方法

针对上文提及的TPC-GPSSM算法存在很多重复计算的问题,进一步对球的建立过程、时态优先级约束等方面进行优化,算法5给出了优化后的TPC-GPSSM算法的伪代码,主要包括：

第一,在球的建立过程中,TPC-GPSSM算法对数据图中每个顶点,都作为中心建立了球,然而其中大量的球并没有包含能够匹配模式图的子图,对这些球的计算浪费了大量时间。在建球之前先进行双向模拟匹配(见第2行),能够过滤掉大量的节点与边,这样既能减少需要建立的球的数量,也能使每个球包含的子图规模减小。

第二,在对球心的选择方面,只选择与模式图中距离最远的两个节点相匹配的节点(见第3-8行),如图1(b)所示,E、D是模式图中距离最远的两个点,以E对应的顶点E2为球心建球得到的结果与以A1为球心建立球得到的结果相同,因此计算以A1为球心的球是冗余的。

第三,在时序优先级约束过程中,先对模式图中的边根据时序优先级进行排序,从高优先级的边开始依次检查,每一条边只检查与其相邻的时序优先级更高的边的之间的时序关系,可避免重复时序检查。

算法5 优化后的TPC-GPSSM算法

输入：时序模式图QT=(Vq,Eq,Lq)及其直径dq,时态图GT=(V,E,L)

输出：子图集合S

1.S：=∅,B：=∅

3.vf1,vf2are the farthest two nodes inQ

4.for eachv∈sim(vf1) or sim(vf2) do

10. forpfrom the highest priority to the lowest priority do

11.simb(v),simb(e')：= TemporalFilter(QT,simb(v),simb(e))

12.Gs：=CheckTopology(QT,simb(v),simb(e))

13. ifGs≠∅ then

14.S：=S∪Gs

15.ReturnS

优化后的TPC-GPSSM算法大幅减少了球的数量,同时避免了球之间因为交集而进行的重复计算,且保证了对每条时序边只检查一次,解决了重复检查的问题。

4 实验与结果分析

本章节对分别从算法有效性以及算法效率两个维度来评估提出的算法,并对普通的强模拟匹配算法[19](General Strong Simulation,GSS)与TPC-GPSSM及优化后的TPC-GPSSM算法进了比较。实验采用三个时态数据集,分别是：(1)BMC[20],一个小学师生相互接触时态网;(2)Enron[21],一个电子邮件传输网络;(3)Wikitalk-Russian[22],一个Russian Wikipedia上的交流网络。表1列出了这些数据集的详细参数,其中|V|、|E|、|T|、#labels分别是数据集的顶点数量、边的数量、边的平均时间区间、标签数量。

表1 数据集

模式图由一个自行开发的模式图生成器提供。给定模式图的顶点数量和标签集合,模式图生成器随机生成包含不同时序优先级数量的模式图。实验对每个数据集分别生成了100个模式图,对其平均结果进行评估。

4.1 算法有效性实验

首先,对TPC-GPSSM算法的有效性进行了实验验证。TPC-GPSSM算法相比传统强模拟匹配算法,能够有效地过滤不符合时态要求的边。为了定量地描述算法有效性,定义了一个评价指标——时态边聚合度(Temporal Edge Closeness,TEC)。

给定一个时序模式图QT=(Vq,Eq,Lq),以及一组作为匹配结果返回的子图{M1,M2,…,Mn},TEC定义如下式：

其中,|EMj|是Mj中时态边的数量,|Eq|是模式图的边数量,TEC的值越小说明对时态边的过滤效果越明显。对三个数据集的实验结果如图2所示,实验改变时序模式图顶点数量|Vq|从2到5,分别在三个数据集上进行测试。其中,GSS由于没有考虑时态边的顺序,所以得到了最大的TEC值,而TPC-GPSSM及其改进算法对不合模式图需求的时态边进行了过滤,得到了更优的TEC值。

图2 不同数据集上匹配质量的评价

4.2 算法效率实验

这里通过二个实验,分别考察时序模式图、不同时序优先级数量对TPC-GPSSM算法效率和性能的影响。

(1)时序模式图顶点数量|Vq|对算法效率的影响。设置了2到10不同大小的|Vq|,在三个数据集上进行了实验。实验结果如图3所示,可以观察到,三种算法的匹配时间都随着|Vq|的增大而增加,这是因为当|Vq|增大时,需要匹配的节点和边的数量也同时增加,这将增加计算的时间花销。优化后的TPC-GPSSM算法采用了先进行双向模拟匹配,再建立球进行局部性检查,使得球的数量大幅减少,取得了更加良好的性能表现。

图3 时序模式图大小对算法效率的影响

(2)不同时序优先级数量对匹配结果的影响。实验中固定模式图的|Vq|为10,改变其中的时序优先级数量,实验结果如图4所示。当时序优先级数量增加时,意味着匹配条件更加严格,符合条件的子图数量也随之减少,而GSS不考虑时序关系,时序优先级数量不影响它的匹配结果。

图4 时序优先级数量对匹配结果的影响

5 结束语

针对时态图上的模式图匹配,提出了一种时序优先级约束的时序模式图强模拟匹配算法(TPC-GPSSM),该算法将时序优先级作为局部约束,在模式图的匹配过程中考虑了时态图中不同时态边之间的时序优先级,并兼顾图的拓扑结构,通过设置冗余顶点过滤规则来缩小搜索范围,优化时序检查的队列顺序,以达到提前剪枝、减少计算复杂度的目的。提出并利用时态边聚合度作为评价指标,在三个时序数据集上的大量实验表明,相比普通的强模拟算法,所提算法能够有效过滤错误结果,并且在不同规模的数据图上均具有良好的性能表现。该算法可应用于涉及前后时序关系的场景,如任务交接分析、交通网络分析等,特别是在任务交接中存在环路的情况下该算法也能进行有效的处理。在下一步的工作中,一个方向是考虑不同时间窗口的约束,另一个方向是在分布式环境中开发更性能更高的算法。