关注图形，研究方法

钱德春

通过“中心对称图形——平行四边形”这一章的学习，我们发现，本章既要掌握几何知识，也要领悟图形研究的内容、路径、策略和方法，感悟其中蕴含的数学思想，为今后图形的研究奠定基础。下面，我们就本章的学习做一些回顾和梳理。

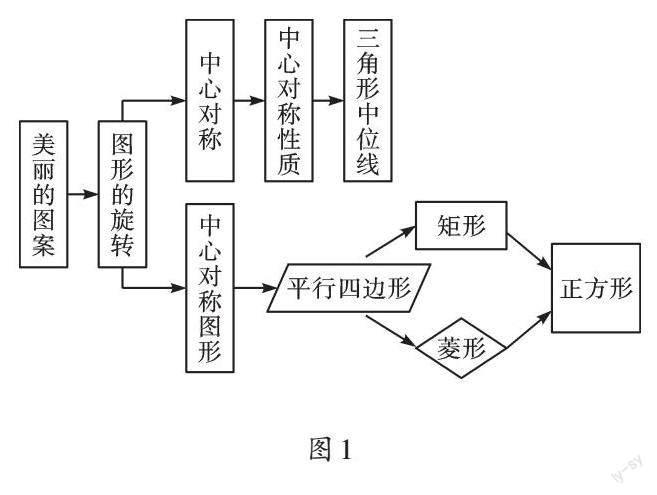
本章的开始，我们通过用数学的眼光欣赏摩天轮、风车的转动等生活中的图案和现象，学习了图形的旋转概念，探索图形旋转的性质，将图形进行180°旋转，引出中心对称和中心对称图形。接着，以中心对称为主线，我们研究了平行四边形以及特殊的平行四边形的判定与性质，利用中心对称研究了三角形中位线的性质（如图1）。最后，我们还对教材的基本问题进行了深入探究，拓展延伸。

例如，教材中有这样一个问题：依次连接任意四边形各边的中点，你能得到什么图形？该问题还可以进行变式思考：如果依次连接矩形各边的中点，你能得到什么图形？如果依次连接一个四边形各边的中点得到菱形，那么原来的四边形一定是矩形吗？依次连接四边形一组对边和两条对角线中点，你能得到什么图形？等等。

在本章的学习中，我们不能只关注中心对称图形相关的知识点，更要关注图形的研究方法、研究路径、推理类型、思维方式和数学思想。从研究路径看，图形研究的一般路径为：定义→性质→判定→运用；从研究方法看，图形研究一般经历操作、观察、发现、推理等过程；从推理类型上看，图形的推理主要分为归纳、类比、演绎。另外，我们要了解反证的思想与方法。从思维方式看，分析图形问题要从两个方面入手，一是从已知想可知，由未知想须知，二是关注知识与方法的联系、图形的转化、方法的迁移；从数学思想看，中心对称图形的研究主体体现为“特殊与一般”和“化复杂为简单”。

如平行四边形、矩形、菱形和正方形等图形之间具有特殊与一般的关系，我们可以感受到：在圖形不断特殊化的过程中，图形的性质越来越多，判定它所需要的条件也越来越多；同时，图形的研究要化复杂为简单，如将四边形问题转化为三角形问题解决。此外，我们还应该学会有条理地思考和表达。这些不仅是我们研究平行四边形的基本要求，也是今后研究其他图形的基本要求。

因此，在数学学习中，我们应该以更广阔的视野，将数学研究的路径、方法、思想迁移到其他领域的学习中，让数学学习指向“诗和远方”。

（作者单位：江苏省泰州市教育局教研室）