失谐螺栓连接对薄壁圆筒的动力特性影响

姚星宇

(中国民用航空飞行学院 航空工程学院，广汉 618307)

在航空发动机结构故障中，整机振动问题[1]一直是制约发动机发展的关键故障问题。研究表明，大量整机振动问题都与连接结构特征参数的公差过于敏感有关[2]。而在连接结构中，螺栓连接结构因其具有构造简单、可操作性好等特点而广泛存在于航空发动机中[3]。但是，螺栓连接在几何上存在突变以及连续性遭破坏，在外载荷作用下，连接处的应力和变形会分布不均，接触和摩擦更是结构阻尼、非线性和能量耗散的主要来源[4]。近年来，航空发动机不断向高转速、高推重比、高使用性、高可靠性和高耐久性发展，使得螺栓连接结构对航空发动机动力特性的影响越来越大。

在航空发动机的设计阶段或理想工作状态时，每个螺栓沿法兰边周向均匀分布且预紧力相同，此时螺栓连接结构是谐调的[5]。但是，对于实际的航空发动机螺栓连接结构，由于每个螺栓安装和装配的差异，螺栓之间的预紧力会不同；航空发动机长时间工作在较恶劣的环境中，随着运行时间的累积，结构中的螺栓连接必然会受到环境的影响。研究表明，疲劳、蠕变、腐蚀、磨损等因素会引起螺栓连接结构的性能退化[6]，其主要表现有：①螺栓预紧力的降低导致连接结构轴向、弯曲刚度的非对称，引起结构的预紧失谐[7]，从而导致结构动力特性的改变；②螺栓预紧力的降低导致连接处刚度下降[8]，从而影响结构的动态特性。当损伤累积到一定程度，必将影响结构之间的正常连接和运转，所以螺栓连接结构的性能退化[9]是航空发动机安全运行必须考虑的问题。本文将安装引起的螺栓预紧力差异和环境因素引起的螺栓性能退化，统称为失谐螺栓连接结构。

为了研究螺栓连接对结构动力特性的影响，研究人员建立了不同的螺栓连接结构参数化模型。精细有限元模型[3,10]最大程度地保留了螺栓连接的几何特征，能够考虑螺栓预紧力及对接面的接触和摩擦作用，因此其模型自由度数庞大，接触非线性会大大增加计算量和计算时间，在航空发动机整机建模中存在局限性，但是在缺少试验结果的基础上，可以将该模型的计算结果当作螺栓连接结构等效简化模型参数修正的依据。弹簧阻尼单元[11-12]将螺栓连接简化为弹簧单元（线性或非线性）和阻尼单元，用刚度系数和阻尼系数来表征连接结构的连接特性，从而降低了模型的自由度数，但是该模型将对接面的面-面接触变成了点-点接触，相应的参数一般需要试验数据来修正，也不能考虑螺栓连接结构的横向移动，因此难以应用在航空发动机建模中。

薄层单元模型[13]克服弹簧阻尼单元模型的局限性，在螺栓连接对接面之间定义了一层能够模拟接触力学特征的虚拟材料，以界面虚拟材料的材料参数来等效模拟实际的界面接触刚度。这些薄层单元是具有参数特性的六面体或四面体单元，能够较为准确地表征连接处的刚度特性，并且能和实体单元相结合建立高保真的整机模型，只是单元的材料参数需要试验数据来修正[14]。对于某些复杂机械结构，由于条件的限制，很多试验难以实施或者根本无法获得合适的试验数据，并且薄层单元法无法考虑螺栓连接接触面应力分布不均的问题。因此，在航空发动机建模和动力特性分析过程中存在一定的局限性和不足。

为了克服薄层单元法的局限性，Yao 等[15]提出了改进薄层单元法，该方法能够考虑对接面应力分布不均的特点，对薄层单元进行分块处理，不同块的单元的材料参数可以通过螺栓连接的载荷、结构参数来确定，而不需要试验数据来修正。因此，螺栓连接的载荷、结构参数的选取将直接决定航空发动机的动力特性。

本文将改进薄层单元法应用到失谐螺栓连接结构中，研究失谐螺栓连接对航空发动机静子薄壁圆筒结构动力特性的影响规律。首先，提出螺栓连接预紧失谐的相关概念，包括预紧失谐量和预紧失谐比例；然后，将航空发动机静子结构简化为薄壁圆筒，研究失谐螺栓连接对薄壁圆筒结构的确定性动力特性分析，包括固有特性和稳态响应；其次，将失谐螺栓连接的相关参数概率化，对考虑螺栓预紧失谐的薄壁圆筒稳态响应进行概率分析。

1 螺栓连接预紧失谐相关概念

螺栓连接结构改进薄层单元法的基本理论在文献[5,15]中有详细描述，本文仅作简单阐述。图1为改进薄层单元法的示意图，其特点为：①可以考虑螺栓对接面应力非均匀分布的特点，薄层单元分块，其中圆形区域为螺栓连接区域，其他区域为法兰边接触区域，不同区域的薄层单元具有不同的材料参数；②不同区域薄层单元的材料参数可通过螺栓载荷、结构参数来理论表达，不需要依靠试验数据来修正，这对研究人员来说，可以在航空发动机设计阶段初期预估结构的固有特性和稳态响应。

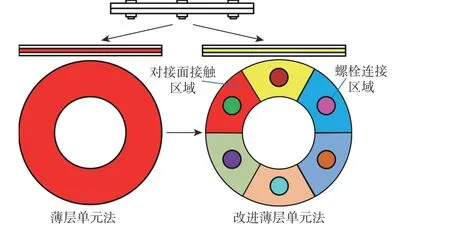
图1 改进薄层单元法Fig.1 Improved thin-layer element method

图2 为某型航空发动机的静子结构，从中可以看出，机匣之间大都通过螺栓进行连接，虽然在结构形式上不同，但是静子结构的螺栓连接具有以下共同点：①螺栓连接结构几乎均具有法兰边；②在大多数情况下连接件都可认为是薄壁圆筒结构；③所承受的载荷大多为轴向力、弯矩、剪切力和扭矩；④螺栓大多沿法兰边周向均布，且数目众多。因此，航空发动机静子结构可简化为由螺栓连接起来的短粗薄壁圆筒结构，如图3 所示。

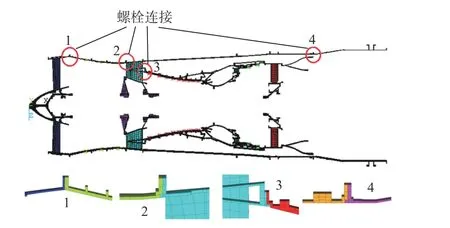
图2 某型航空发动机静子结构Fig.2 Stator structure of aero engine

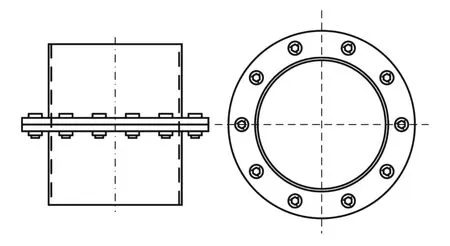
图3 薄壁圆筒螺栓连接结构Fig.3 Bolted joints structure of thin-walled cylinder

设N为法兰边周向螺栓个数，F为每个螺栓预定的螺栓预紧力，当螺栓连接结构发生预紧失谐时，失谐的螺栓个数为p。

定义每个螺栓i的预紧失谐量（preload mistuning amplitude）ϕ为

式中：Fi′为螺栓连接结构第i个螺栓的实际预紧力；ϕi> 0 为预紧正失谐，ϕi< 0 为预紧负失谐，ϕi=0 为预紧谐调。对于安装装配原因引起的预紧失谐，可能出现正失谐和负失谐，而环境因素引起的螺栓性能退化，则会出现负失谐，本文只讨论预紧负失谐。

定义螺栓连接结构的预紧失谐比例（preload mistuning ratio）β为

本文将以这2 个参数来表征螺栓连接结构的失谐状况。

2 失谐螺栓对薄壁圆筒的确定性动力特性影响

2.1 失谐螺栓连接薄壁圆筒结构建模

该结构是由2 个完全相同的带法兰边的圆筒结构通过12 个M20 的螺栓连接起来，其相关尺寸参数如图4 所示，圆筒部分和螺栓的材料属性相同，其材料参数如表1 所示。

表1 圆筒和螺栓的材料参数Table 1 Material parameters of cylinder and bolts

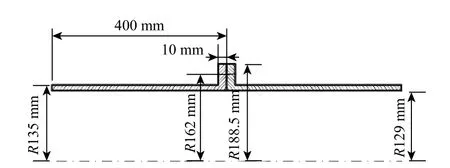
图4 带螺栓的薄壁圆筒结构Fig.4 Thin-walled cylinder structure with bolts

根据改进薄层单元法[15]，得到了不同预紧力下薄层单元的材料参数，如表2 所示，其中G为剪切模量。假设预定的F为25 000 N，ϕ分别为−20%、−40%、−60%和−80%，β分别为1/6、1/3、1/2 和2/3。螺栓连接处的有限元模型如图5 所示，其中2 个横向方向为x向和y向，预紧失谐螺栓关于薄壁圆筒的x向对称。

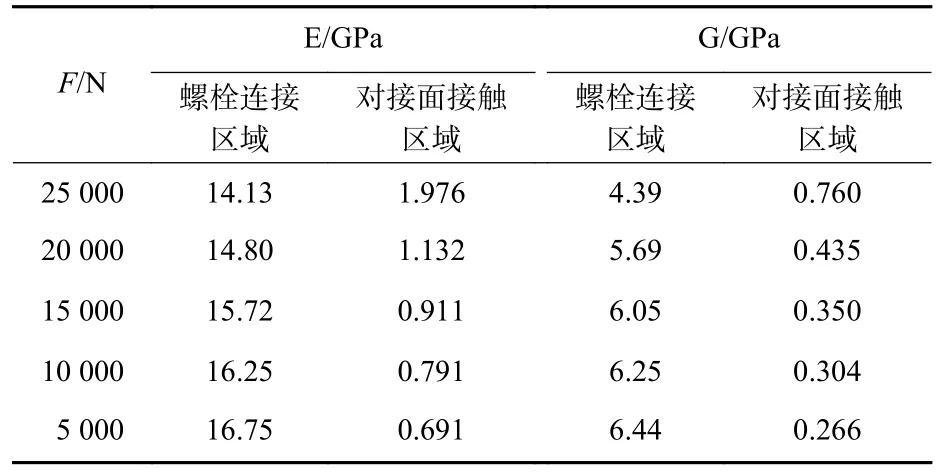
表2 薄层单元的材料参数Table 2 Material parameters of thin-layer elements

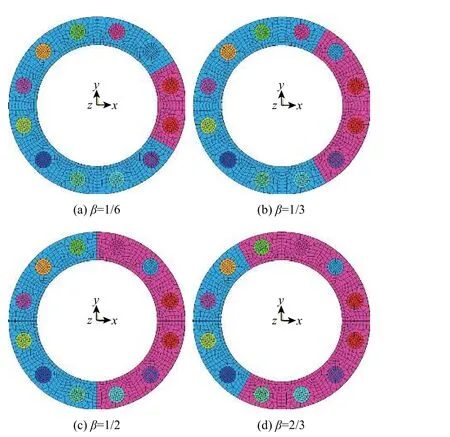
图5 螺栓连接处的有限元模型Fig.5 Finite element model of bolted joints area

2.2 固有特性影响

对预紧失谐的薄壁圆筒进行固有特性分析，结构的边界条件为两端自由，提取模型前6 阶固有频率，如表3 所示。

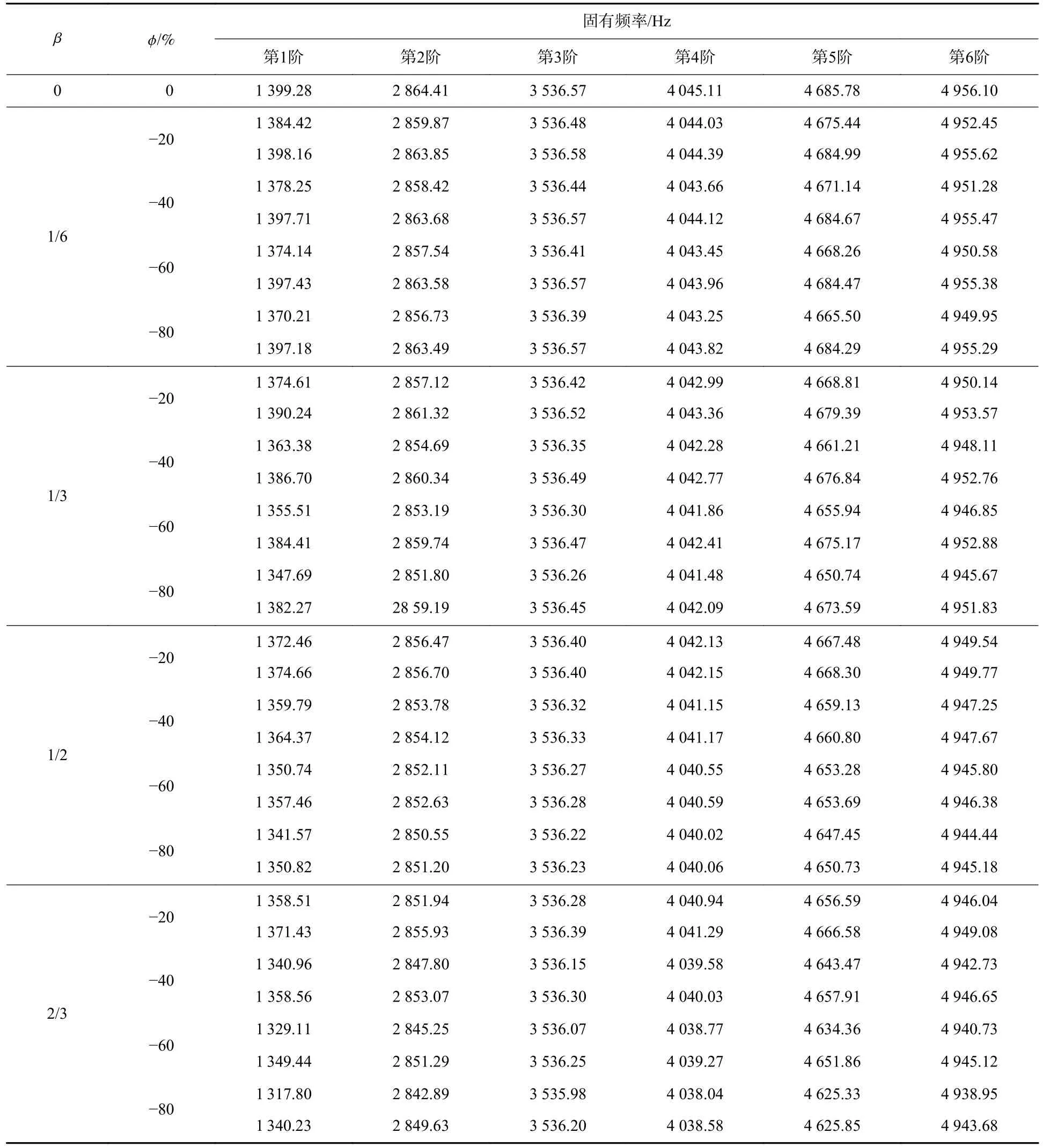
表3 不同 β和 ϕ下薄壁圆筒的前6 阶固有频率Table 3 The first 6-order natural frequencies of thin-walled cylinder under different β and ϕ

1）与谐调螺栓连接的薄壁圆筒相比，预紧失谐薄壁圆筒的固有频率均减小，这说明当螺栓连接结构存在预紧失谐且ϕ<0 时，螺栓连接的连接刚度降低，从而使得结构的弯曲固有频率降低。

2）预紧失谐对薄壁圆筒各阶横向弯曲固有振动的影响程度不同，图6 为预紧失谐量 ϕ对薄壁圆筒固有频率的影响曲线（β=1/3），随着 ϕ的降低，第1 阶振动固有频率的下降程度大于其他阶振动，这说明该薄壁圆筒的第1 阶横向弯曲振动对 ϕ最为敏感，这与谐调螺栓连接情况下螺栓预紧力F对薄壁圆筒固有频率影响规律一致[5]。

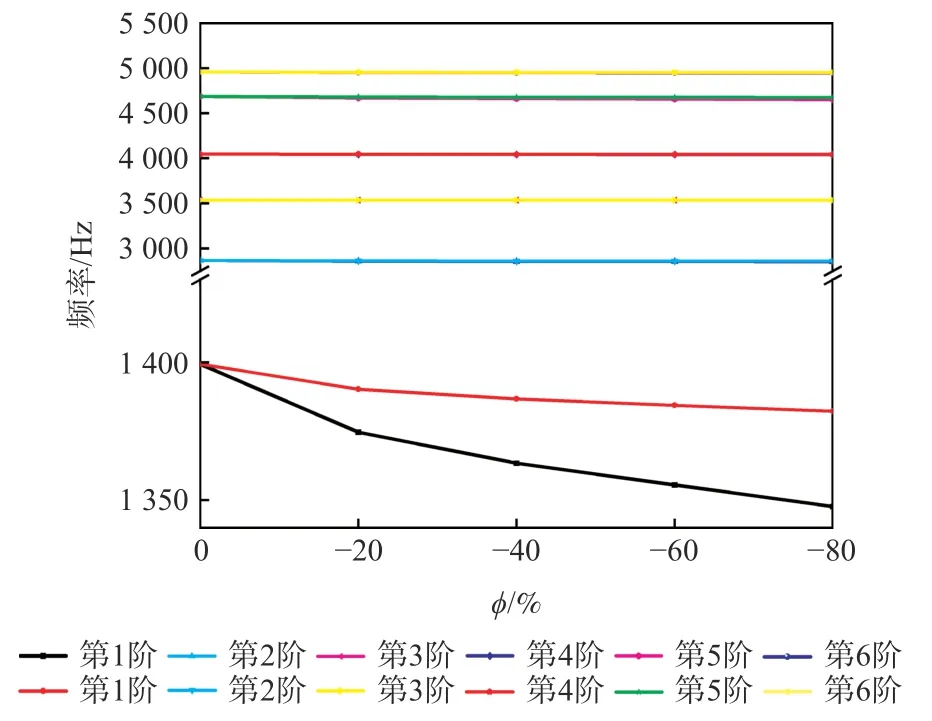
图6 ϕ对薄壁圆筒固有频率的影响曲线( β=1/3)Fig.6 Influence of ϕ on natural frequency of thin-walled cylinder ( β=1/3)

3）当 β一 定、ϕ<0 且逐渐减小时，2 个横向方向的同阶振动固有频率值会发生分离，并且分离程度会随着 ϕ的逐渐减小而增大。图7（a）为 ϕ对薄壁圆筒第1 阶固有频率分离程度影响曲线，当ϕ=0 时，2个横向方向的第1 阶固有频率值相等，均为1 399.28 Hz，分离程度为0 Hz；当 β= 1/6、ϕ逐渐减小时，2 个横向方向的第1 阶固有频率值逐渐分离，并且分离程度越来越大，频率差值从谐调时的0 Hz 变为ϕ=−80%的26.97 Hz，这说明预紧失谐会使得薄壁圆筒周向螺栓连接结构的刚度非对称，并且非对称的程度与ϕ成正比。

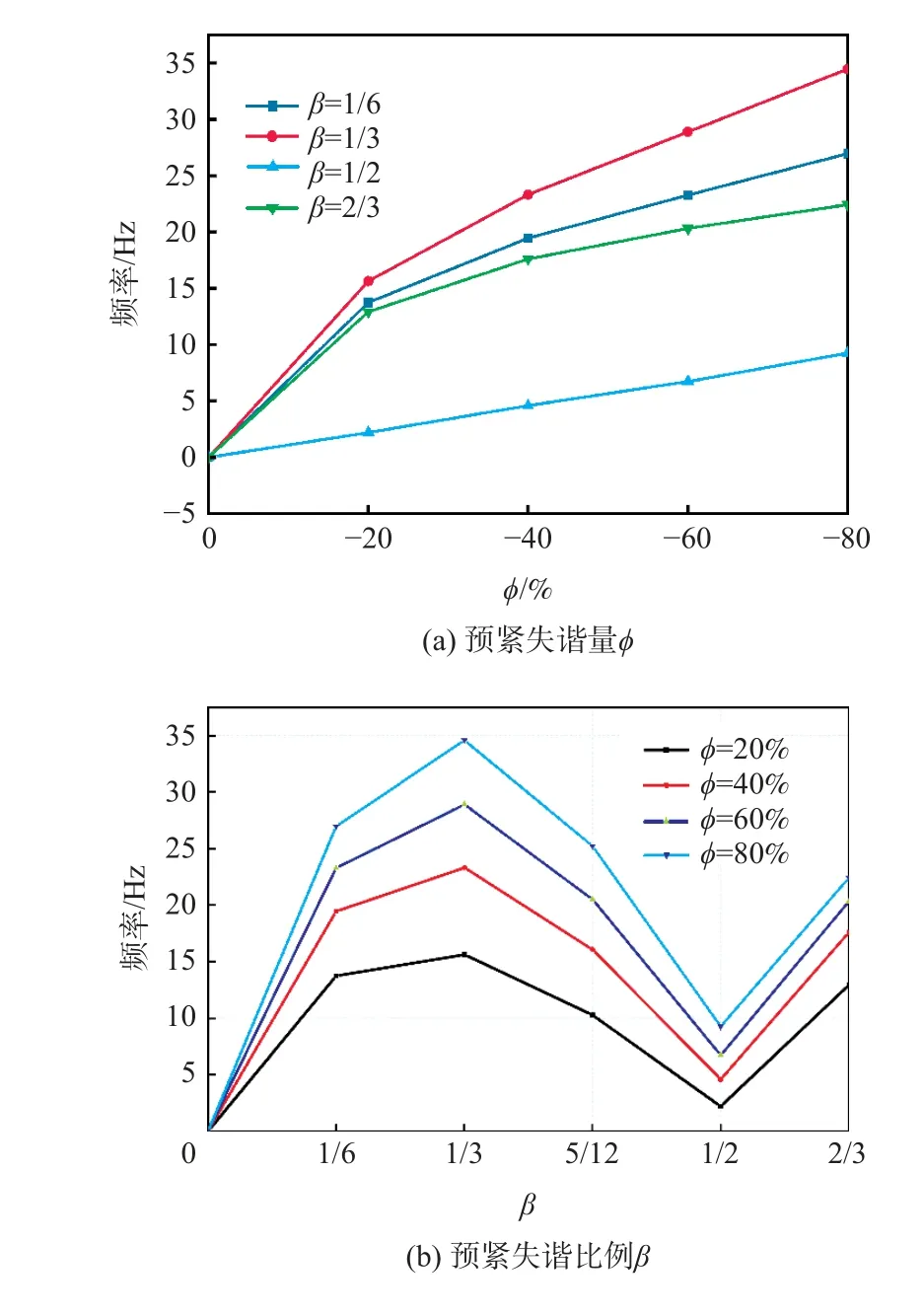
图7 ϕ 和 β对薄壁圆筒第1 阶固有频率分离程度的影响Fig.7 Influence of ϕ and β on the first order natural frequency separation of thin-walled cylinder

4）当 ϕ一 定、β逐渐增大时，2 个横向方向的同阶振动固有频率值的分离程度是先增大再减小，到β=1/2 时减到最小，然后又逐渐升高，升高到一定程度后又逐渐减小，当 β=1 时减为0，如图7（b）所示。这说明，随着 β的增大，周向螺栓连接刚度的非对称程度是由0 开始增大，然后减小再增大，最后再减小到0 的过程，其中非对称程度的极大值点在预紧失谐比例 β接近1/4 或3/4 时，极小值点是 β接近0、1/2 和1 时，呈现明显的“双峰”特点。

2.3 稳态响应影响

在实际的静子结构中（见图2），载荷是由转子系统的转子部分（如叶片）通过轴-轴承-支承框架，传递到静子结构的机匣处，最终通过发动机与机翼之间的安装节传递到飞机机身上。由于静子结构的机匣（薄壁圆筒）大都通过螺栓一段一段地连接，相较于机匣的刚性，支承框架的刚度要远远大于机匣，所以考虑薄壁圆筒的稳态响应分析时，可将薄壁圆筒的一端固定（模拟支承框架的大刚度），另一端的y向接点处施加大小为100 N 的载荷（模拟从转子部分传递过来的载荷），结构阻尼系数为0.000 2，应用模态叠加法计算结构的稳态响应，计算范围为0～1 500 Hz，计算载荷步为750 步，如图8 所示。本节将从2 个方面讨论失谐螺栓连接对薄壁圆筒响应特性的影响：①预紧谐调结构和预紧失谐结构响应的比较；②ϕ和 β对薄壁圆筒响应特性的影响。

图8 薄壁圆筒的边界条件Fig.8 Boundary conditions of thin-walled cylinder

1 ）预紧谐调结构和预紧失谐结构的比较

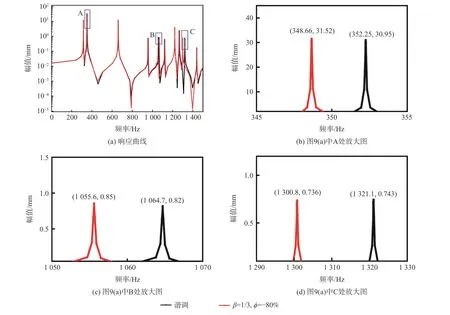
图9 预紧谐调与预紧失谐薄壁圆筒响应曲线Fig.9 Response of thin-walled cylinder with tuning preload and mistuning preload

① 预紧失谐薄壁圆筒的峰值点较预紧谐调结构的峰值点所对应的频率减小，这是预紧负失谐使结构的连接刚度降低造成的。

② 预紧负失谐对不同峰值所对应的频率减小幅度的影响程度不同。

③ 预紧负失谐的响应最大幅值（31.52 mm）大于谐调结构的最大幅值（30.95 mm），增幅约为2%。

2 ）ϕ 和 β的影响

图10 为 ϕ和 β对薄壁圆筒响应的影响曲线，提取的仍是y向位移，从中可以看出：

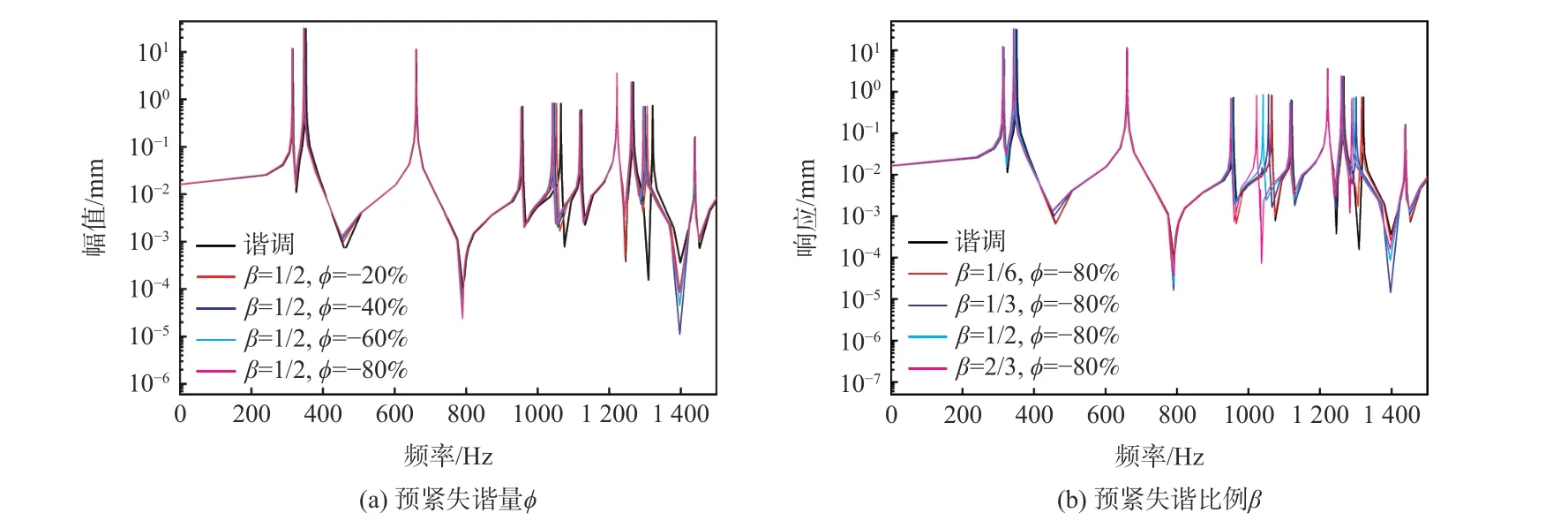
图10 ϕ 和 β对薄壁圆筒响应的影响Fig.10 Influence of ϕ and β on response of structure

① 当 β一定时，随着 ϕ的降低，响应曲线的峰值点所对应的频率减小，且同个峰值点的响应幅值逐渐增大，这是螺栓连接处连接刚度降低导致。

② 当 ϕ一定时，随着 β的增大，响应曲线的峰值点所对应的频率减小，同峰值点幅值逐渐增大。

以前我东奔西跑地，很少呆在车间里，现在有机会和员工们好好沟通交流了。员工们对我很尊重，一口一个厂长。我进景花厂这么久了，仍不习惯被人叫做厂长。我不端厂长的架子，手把手地教他们抛光工艺，不烦不躁，耐心指导。不但培养他们的技术，还培养与他们的感情。只有和他们建立了情谊，才能留住人心。大发厂过去培养了我，我对大发厂至今仍有感情。但对林强信我没有感情，他一进车间，我们就像见了鬼。所以在权衡去留时，我为大发厂洒了几滴清泪，但还是离开了，因为林强信在我心中没有分量。

③ β和 ϕ对不同峰值所对应的频率减小幅度的影响程度有差异，对结构横向弯曲振动的影响大于对结构局部波形振动的影响。

3 失谐螺栓连接对薄壁圆筒的概率性动力特性影响

从第2 节分析看出，螺栓连接预紧失谐对薄壁圆筒的动力特性有较大影响。在很多情况下，螺栓连接结构周向每个螺栓的预紧情况有差异，预紧失谐存在随机性，因此很难准确预测薄壁圆筒的响应状态。本节将对考虑螺栓预紧失谐的薄壁圆筒的稳态响应进行概率分析。

3.1 随机输入参数和输出参数的确定

当螺栓连接结构发生预紧失谐后，薄壁圆筒随机动力学方程为（忽略预紧力变化对结构阻尼的影响）

式中：N为螺栓个数；M、C分别为系统质量、阻尼矩阵；KBTLi、KFTLi和KRTL分别为第i个螺栓连接区域、法兰边接触区域的薄层单元刚度矩阵和除去薄层单元以外的单元刚度矩阵（相应的区域如图5 所示）；j为抽样次数，∆KBTLj和 ∆KFTLj分 别为第j次抽样后第i个螺栓连接区域薄层单元的偏移刚度矩阵和第i个法兰边接触区域薄层单元的偏移刚度矩阵；x¨、x˙、x和f分别为加速度向量、速度向量、位移向量和外载荷向量。

一般认为，螺栓预紧力F由于安装、装配的差异以及螺栓性能退化等因素所产生的失谐服从指数分布[6]，但是螺栓预紧力不能作为随机参数在薄壁圆筒有限元模型中体现，因此需要选取一个能够表征螺栓预紧力F预紧失谐状况的参数作为随机输入参数。

本节仍以前面所述的薄壁圆筒（见图5）为例，假设螺栓连接结构每个螺栓的预紧力F=25 000 N，当F由于螺栓性能退化逐渐减小时，法兰边接触区域薄层单元的弹性模量E1会逐渐减小，因此选取每个扇区的E1作 为随机输入参数。当E1发生变化时，螺栓连接区域薄层单元的弹性模量E2也会跟着改变，所以首先需要确定E2与E1之间的关系。

由改进薄层单元法可知[15]，E2的获得需要每个螺栓扇区薄层单元的刚度KTL和 厚度L、法兰边接触区域的面积A1和E1以 及螺栓连接区域的面积A2。在建模过程中，假设螺栓连接区域半径是常数，不会随着预紧力F的改变而改变，那么不同预紧力F条件下螺栓连接结构处的相关数据如表4 所示，通过表中数据，拟合得到每个扇区的KTL与E1之间的关系（见图11）表达式为

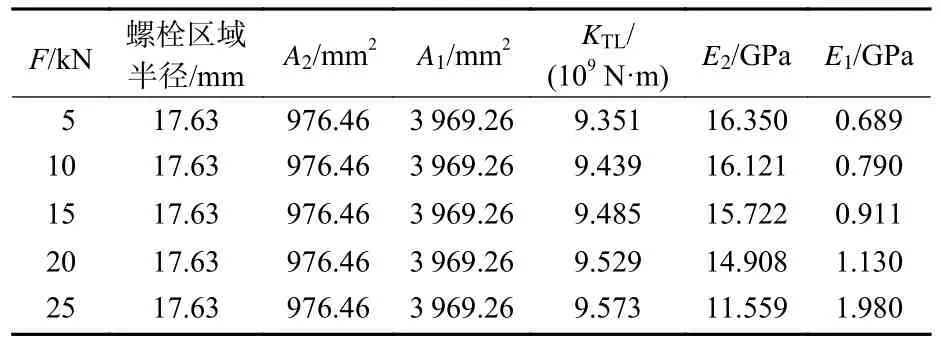
表4 不同预紧力F 下螺栓连接处的数据Table 4 Data of bolted joints under different preloads F

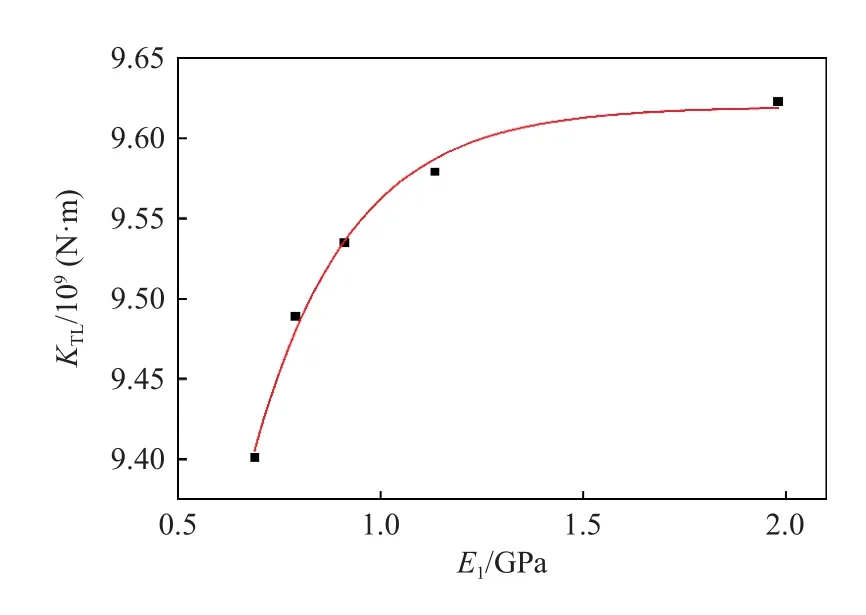
图11 E1 与KTL 的关系Fig.11 Relationship between E1 and KTL

对于图5 所示的螺栓连接区域，每个螺栓所在扇区的刚度表达为

因此，螺栓连接区域的弹性模量E2可表示为

对薄壁圆筒进行有限元建模，将E1作为输入参数，设置为指数分布（见图12），其中初始值为1.98 GPa，衰减系数为0.00 371，最终得到薄壁圆筒的随机有限元模型，其中螺栓连接处模型如图13 所示，每个扇区不同区域的材料参数是不同的，从而模拟螺栓连接结构的随机预紧失谐。此时，对每个扇区的E1进 行抽样，便可得到第j次抽样后第i个螺栓连接区域薄层单元和法兰边接触区域薄层单元的偏移刚度矩阵。

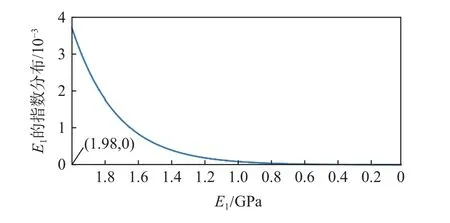
图12 E1 的指数分布Fig.12 Exponential distribution of E1

图13 失谐时螺栓连接处的有限元模型Fig.13 Finite element model of mistuning bolted joints

应用完全法对式(3)进行求解，计算结构的稳态响应，计算范围为0～1 500 Hz，计算步长为0.5 Hz，加载方式与第2 节一样，选取加载点y向、x向的响应幅值作为输出参数。

3.2 结果分析

运用Monte Carlo 法进行求解，抽样次数为100 次，抽样方法为拉丁超立方抽样。薄壁圆筒加载点的y向、x向随机响应曲线分别如图14 所示。从中可以看出：

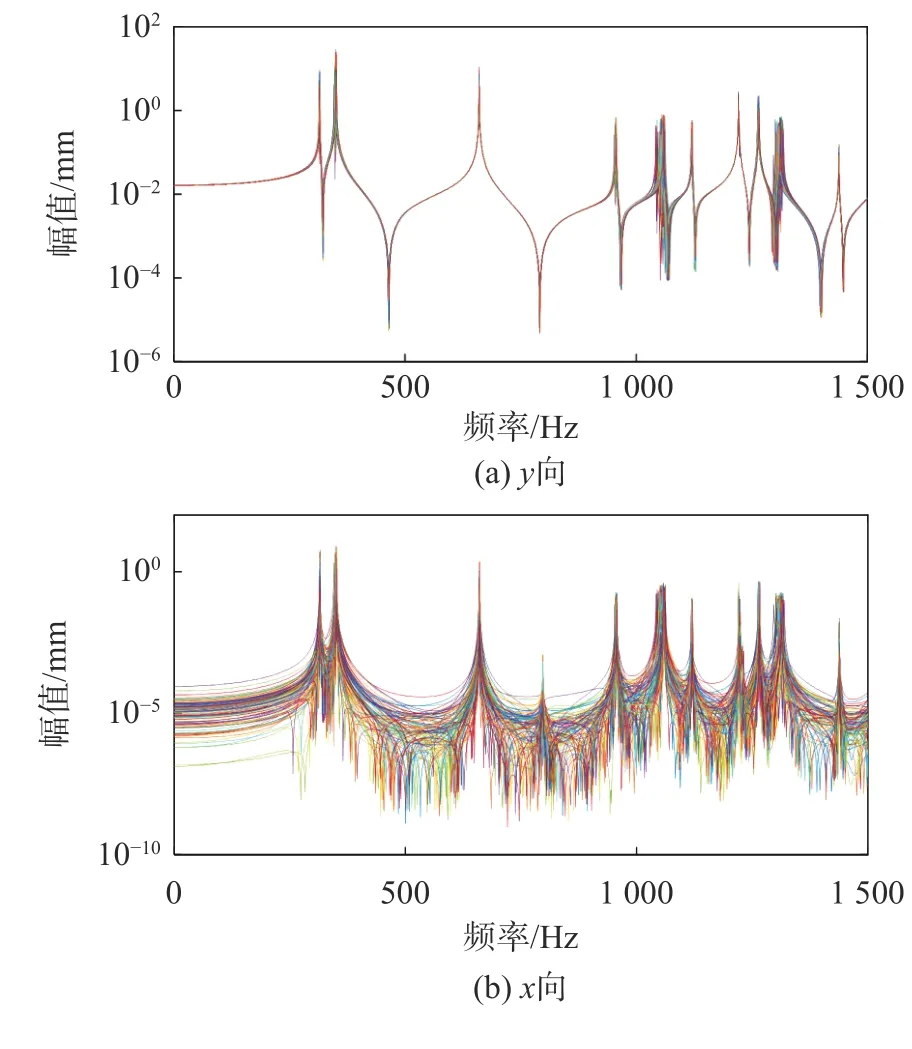
图14 薄壁圆筒加载点y 向和x 向的随机响应曲线Fig.14 Random response curves of load point in y and x direction of thin-walled cylinder

1）随机预紧失谐会使结构响应峰值点的频带更宽，特别对于整体结构的弯曲振动影响更大。

2）当加载方向为y向时，x向响应也会出现响应峰值，说明预紧失谐会引起与加载方向垂直的横向方向的振动。

3）y向响应曲线峰值点的幅值均不同，说明预紧失谐可能会使结构响应幅值放大。

输入参数和输出参数的概率密度函数如图15所示，可以看出，输入参数为不同区域的法兰边接触区域弹性模量，符合指数分布，初始值为1.98 GPa，衰减系数为0.003 71，而对于输出参数加载点y向某个频率下的响应幅值则大致符合威布尔分布，这说明在航空发动机工作过程中，螺栓连接结构都会发生预紧力下降，从而发生预紧失谐，但是当预紧力下降到一定程度时，螺栓连接结构的预紧状况呈现稳定的状态。

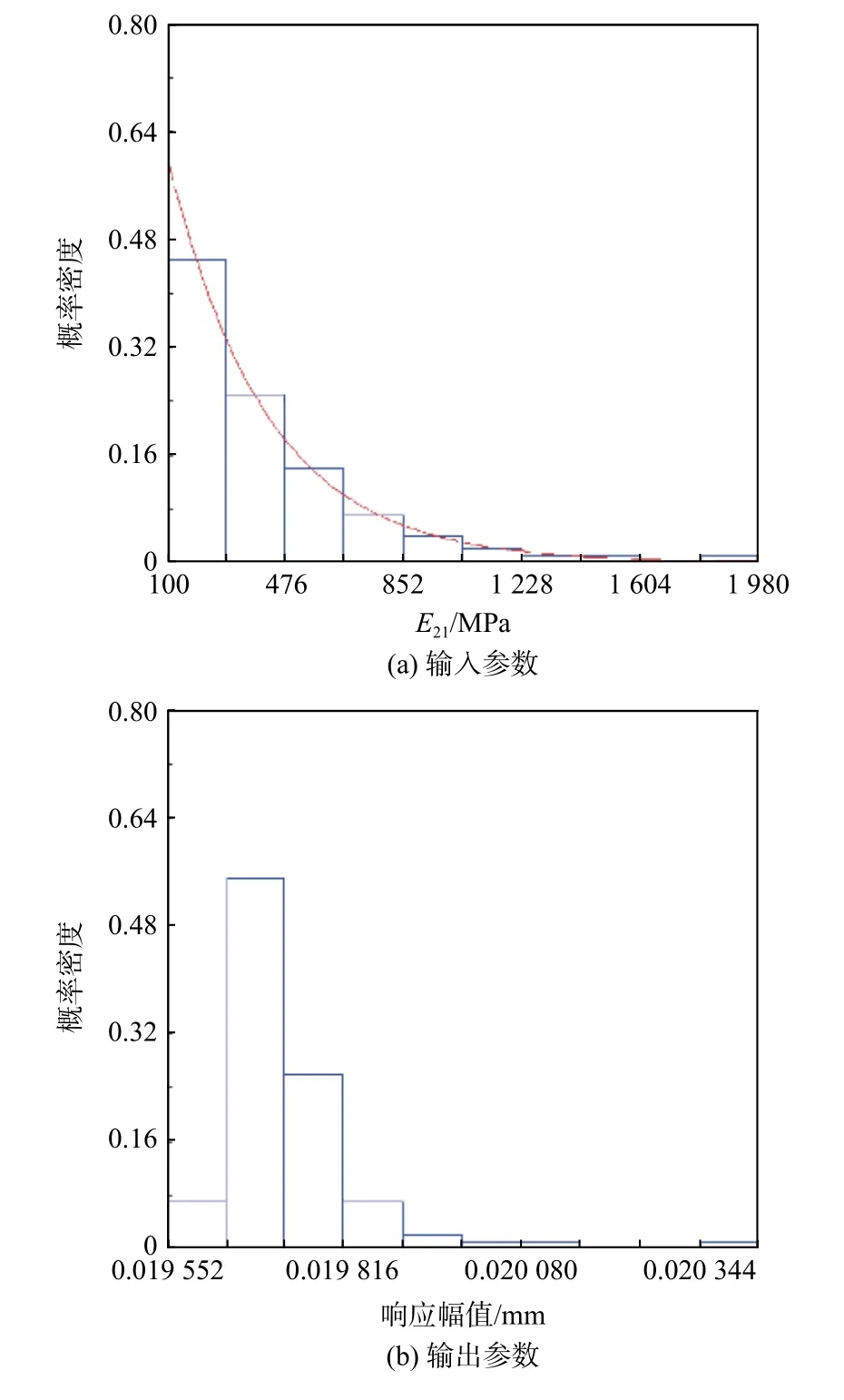
图15 薄壁圆筒输入、输出参数的概率分布Fig.15 Probability distribution of input and output parameters of thin-walled cylinder

4 结 论

1）预紧失谐会使薄壁圆筒的每阶固有频率下降，但不同阶的频率下降程度不同，对第1 阶弯曲振动的影响最明显。

2）β和 ϕ对 薄壁圆筒固有频率影响不同，当 ϕ逐渐减小时，同阶弯曲振动的固有频率值会发生分离，且分离程度随着 ϕ的减小而增大；当 β逐渐增大时，同阶弯曲振动的固有频率分离程度呈现明显的“双峰”特点。

3）预紧失谐使得薄壁圆筒响应峰值所对应的频率减小且幅值增大，并且对整体结构弯曲振动的影响要大于圆筒结构局部的波形振动。

4）随机预紧失谐使得薄壁圆筒的响应峰值点的频带更宽，输入参数E1为指数分布，初始参数为1.98 GPa，衰 减 系 数 为0.003 71，输 出 参 数 加 载 点y向响应大体符合威布尔分布，说明航空发动机在工作过程中，螺栓预紧力均会发生预紧失谐，但失谐到一定程度之后，螺栓连接的预紧状况呈现稳定的状态。