基于CEEMD 与改进的ELM 旋转整流器故障诊断

朱佩荣，刘勇智，刘棕成，陈俊柏，聂恺

(1.空军工程大学 研究生院，西安 710038；2.空军工程大学 航空工程学院，西安 710038)

多电/全电飞机的应用迅猛发展[1]，这对飞机供电系统的稳定性提出了更高要求[2]。三级式无刷同步发电机是当前飞机主电源系统的关键设备，其一旦发生故障将严重影响飞机的飞行安全[3]。文献[4]针对三级式同步电机故障模式，结合基于危害程度矩阵定量分析的方法指出，旋转整流器二极管故障是同步交流发电机故障模式中频率最高且需要优先考虑的故障。因此，为提高飞行的安全，在旋转整流器故障时，必须采取措施，及时准确地对故障进行检测。

旋转整流器故障诊断流程主要包括信号采集、提取故障特征和故障分类[5]。目前针对航空发电机旋转整流器的故障特征提取与诊断方法分为以下3 类。

1）基于解析模型的故障诊断[6-7]。该方法深入分析发电机的运行原理，建立准确的系统解析模型。通过可观测输入输出量构成残差信号，然后对残差信号进一步地分析和处理，达到故障仿真、故障分析和故障诊断的目的。文献[6]通过对发电机进行相域建模分析，并利用观测器来判断飞机发电机旋转整流器是否故障。文献[7]定性分析发电机励磁电流与输出电压的关系，来实现对旋转整流器的故障诊断。这种故障诊断方法需要对系统的运行机理有充分的认识，当模型与实际系统一致时，故障诊断准确率很高。但是由于发电机是一个非线性、强耦合、多参数的系统，很难准确建立其真实模型。

2）基于信号分析的故障诊断[8-10]。该方法是对反应故障的可测信号进行信号分析与故障特征提取。其中最典型的方法是对励磁电流信号进行傅里叶变换（Fourier transform，FFT）分析[8],但FFT 分析更适合处理平稳信号，而故障状态下的励磁电流信号一般是非平稳信号。针对励磁电流信号非平稳、非线性的特点，文献[9]提出对励磁电流基于小波包分解的时频分析，以第1～第7 层能量系数作为故障特征。该方法对故障特征提取较为准确，但是小波包分析存在小波基函数不具备适应性的问题。文献[10]通过经验模态分解（empirical mode decomposition，EMD）对励磁电流信号进行故障特征提取，克服了基函数无自适应性的问题，但EMD的分解方法也会带来频率混叠的现象。

3）基于智能算法的故障诊断[11-13]。随着智能算法的成熟发展，其已被广泛的应用到电机故障诊断领域。文献[11]利用基于灰色关联度分析的堆栈自动编码器（stack autoencoder，SAE）方法对励磁电流信号实现故障特征，同时利用分类器对所提取的特征实现故障诊断。文献[12]提出基于深度置信网络（depth belief network，DBN）的故障特征提取方法，并利用BP 神经网络实现故障分类。文献[13]将宽度学习（broad learning system，BLS）引入航空发电机旋转整流器的故障特征提取中。但智能算法缺点是在系统很大、数据量很多的情况下，网络的建立和训练需要花费较长的时间。

为解决上述3 类故障诊断方法的问题，本文首先在有限元软件Maxwell 与Simplorer 搭建三级式同步电机非线性模型，并采集励磁电流信号分析处理，提出基于CEEMD 与改进的极限学习机（extreme learning machine，ELM）无刷同步发电机旋转整流器故障诊断的方法。CEEMD 能对励磁电流信号自适应故障特征提取，同时抑制了模态混合问题。ELM 相比于传统分类器BP、支持向量机（support vector machine，SVM）等具有分类速度快、泛化能力强的特点，在快速故障诊断中具备较大优势。但ELM 的缺点是其性能取决于训练参数 ω和b，两者在模型建立中容易陷入局部最优，因此，本文提出了基于樽海鞘群算法（salps algorithm，SSA）优化的ELM 故障诊断模型，并在相同的研究环境下，与遗传优化算法、粒子群优化算法进行对比分析。

1 基于Maxwell 与Simplorer 同步发电机非线性建模

目前航空发电机大部分为三级式无刷同步发电机，主要包括副励磁机（永磁机）、主励磁机、旋转整流器、主发电机、调压器5 部分。本文以某型115 V/400 Hz 三级式同步发电机为研究对象。

在Maxwell 中分别搭建副励磁机、主励磁机、主发电机模型。以主发电机为例，其模型基本参数如表1 所示，定转子磁钢材料为DW465_50。主发电机有限元2D 模型如图1 所示。

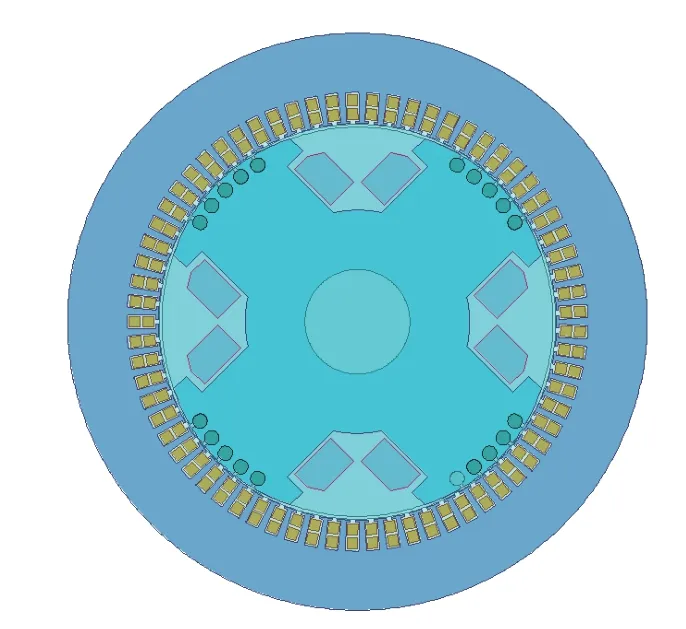
图1 主发电机有限元2D 模型Fig.1 2D finite element model of main generator

表1 主发电机基本参数Table 1 Basic parameters of main generator

将副励磁机、主励磁机、主发电机模型分别导入有限元软件Simplorer 中，并在Simplorer 中搭建旋转整流器模块与调压器模块，设置求解器仿真步长为100 µs，仿真时间为45 ms，三级式同步电机整体模型与调压器模型分别如图2 和图3 所示，D1～D10均为二极管，I1 为调压器输出信号，w(t)为电机转速，VM1～VM3 为主发电机三相输出电压，GND 表示接地，1/S 为积分模块，GAIN 为增益模块，COMP为信号比较模块，RMS 为有效值计算模块，Urmf为参考电压。

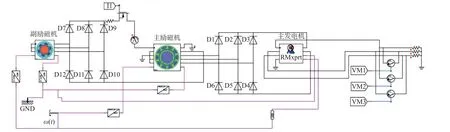
图2 三级式同步电机整体模型Fig.2 Integral model of three stage synchronous motor

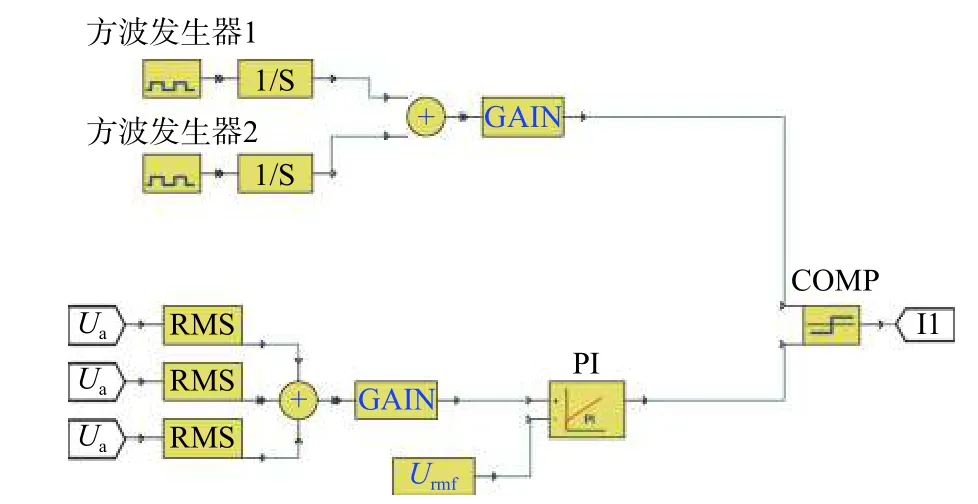
图3 调压器模型Fig.3 Voltage regulator model

由图2 可知，连接主励磁机与主发电机的旋转整流器由6 个二极管D1～D6 组成，角速度模块中设置电机转速为12 000 r/min。

由图3 可知，调压器通过采集主发电机输出三相电压的有效值，与给定参考电压比较，产生误差经比例积分微分（PID）控制器校正，再与三角波交截产生脉宽可调的脉冲宽度调制（pulse width modulation，PWM）波，驱动主励磁机上的功率开关管，实现控制主励磁机励磁电流最终达到调压目的。经调试PID 参数设置为：比例增益KP=25，积分增益KI= 370，微分增益KD=0.05。

三级式同步发电机模型运行后，主发电机三相输出电压波形如图4 所示。图中Ua1、Ub1、Uc1分别为主发电机三相输出电压，在主发电机输出电压波形中随机选取m1、m2、m3这3 点可得，经过PID 调压器调压后，主发电机输出电压满足400 Hz/115 V 的要求，验证了模型的准确性。

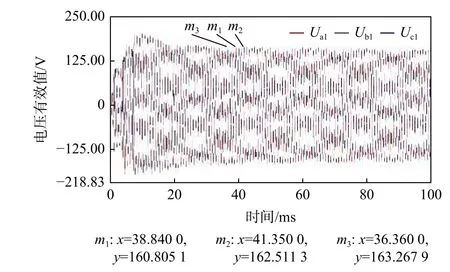
图4 主发电机三相输出电压波形Fig.4 Three phase output voltage waveform of main generator

2 CEEMD 与ELM

2.1 CEEMD 方法

EMD 自适应的将非平稳时间序列信号s(t)分解为n阶相对平稳的的本征模态函数（intrinsic mode function，IMF）及一个标准的残差量[14]。记为

式中：Mi(t)为 第i阶IMF 分量；Re(t)为残差量。

为抑制EMD 中模态混合问题，CEEMD 首先在信号处理的整个时频段加入正、负相对的高斯白噪声。记为

随后分别对加入的正、负高斯白噪声序列信号进行经验模态分解，得到对应的IMF 分量与残差量，再对正、负高斯噪声下的各IMF 分量与残差量Re(t)求取平均值，作为CEEMD 信号处理的最终结果，表达式为

式中：Cm和Re分别为CEEMD 信号处理后得到的第m个IMF 分量与Re(t)残 差量；Cim和C−im分别为正、负 高 斯 白 噪 声 下s+j(t)与s−j(t)分 解 的 第m个IMF分量；Rei和R−ei为 正负高斯白噪声下s+j(t)与s−j(t)分解的残差量。

CEEMD 信号分解流程如图5 所示。

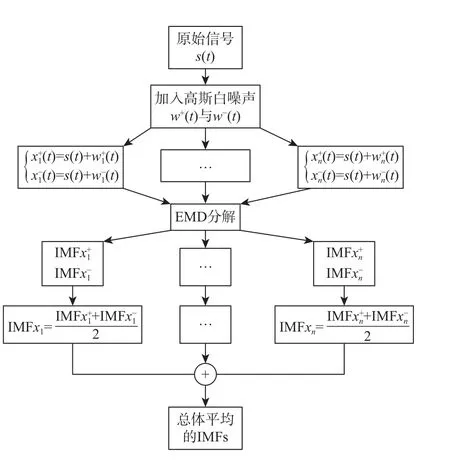
图5 CEEMD 信号分解流程Fig.5 Signal decomposition flow chart of CEEMD

2.2 改进的ELM 方法

2.2.1 ELM 方 法

ELM 是一种单隐层的前馈神经元网络[15]，训练过程中输入层和隐含层之间的连接权值 ω和隐含层的阈值b可以随机设定，设定后无需进行调整，隐含层与输出层的连接权值通过解方程求得，无需迭代产生。ELM 的计算特征在保证学习精度的前提下让其算法速度更快。假设有N个任意的样本(Xl，tl)，其中Xl、tl均为一个l维列向量。对于一个有H个隐层节点的单隐层神经网络，为使输出无误差，其可以表示为

式中：Wl为 输出权重；ωl为输入权重；bl为 第l个隐层单元的偏置向量；g(x)为激活函数；ωl·Xl表示 ωl与Xl的内积。

式（4）可简化为

式中：H为隐含层输出矩阵；β为隐层与输出层间的权矩阵；T为期望输出矩阵。

则输出层权值为

式中：H+为 隐藏层输出矩阵H的广义摩尔逆矩阵。

2.2.2 基于SSA 的ELM 方法

传统群优化算法中(如粒子群，蚁群，灰狼群等) ，因领导者前期搜索不充分而容易陷入局部最优问题，SSA 利用“链”结构模式有效避免了此缺点且该算法能够有效寻找全局最优解。因此，本文采取SSA 对ELM 的权值 ω 和 偏置b进行优化，从而得 到 最 优 的 ωbest与bbest。

设置参数优化后的目标函数为

式中：yˆa为权值 ω和偏置b的 期望值；ya为a次寻优后权值 ω 和 偏置b的实际值。

对数据预处理选取训练集，并根据目标函数，构建基于SSA 优化输入权值 ω 和 偏置b的ELM 分类模型，对CEEMD 的特征向量分类处理，其流程如图6 所示。

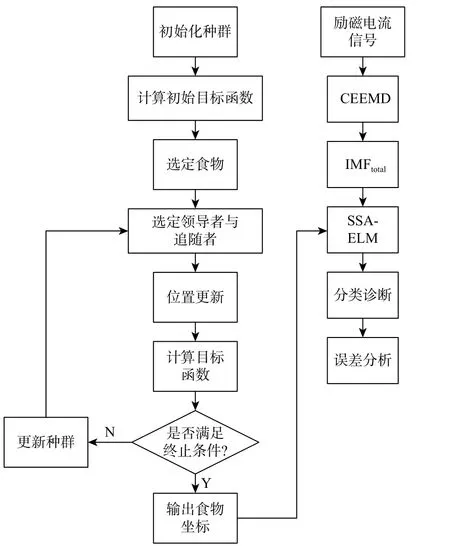
图6 SSA-ELM 算法流程Fig.6 Flow chart of SSA-ELM algorithm

3 仿真实验

3.1 故障模式分类与信号采集

本文研究旋转整流器二极管开路故障，为对比分析，将二极管正常状态定义为特殊故障状态，最终得到二极管开路故障下的5 类故障状态，如表2 所示，2 个二极管之间不加逗号表示这2 个二极管同时故障。

表2 二极管开路故障下的5 类故障状态Table 2 Five kinds of fault states under diode open circuit fault

由于旋转整流器位于三级式同步发电机转子上，高速旋转下无法准确的获取其内部的故障信号。考虑到旋转整流器二极管故障时，主励磁机的电枢绕组的电流会处于不对称状态，最终通过电磁感应现象，主励磁机励磁电流将产生交流谐波成分。因此，可选择励磁电流作为旋转整流器二极管故障的检测信号。

考虑到负载对发电机运行状态的影响，分别在负载条件为空载、1.5 kW 负载、3 kW 下进行数据采集，每种负载条件下每种类型故障采集样本100组。由于发电机实际运行过程中，负载可能发生改变，故将不同负载类型样本数据混合在一起，即共计1 500 组励磁电流数据，其中按照1∶1 比例将数据样本分为训练集与测试集。以发电机空载为例，旋转整流器二极管处于开路的5 类故障状态下的励磁电流信号如图7 所示。

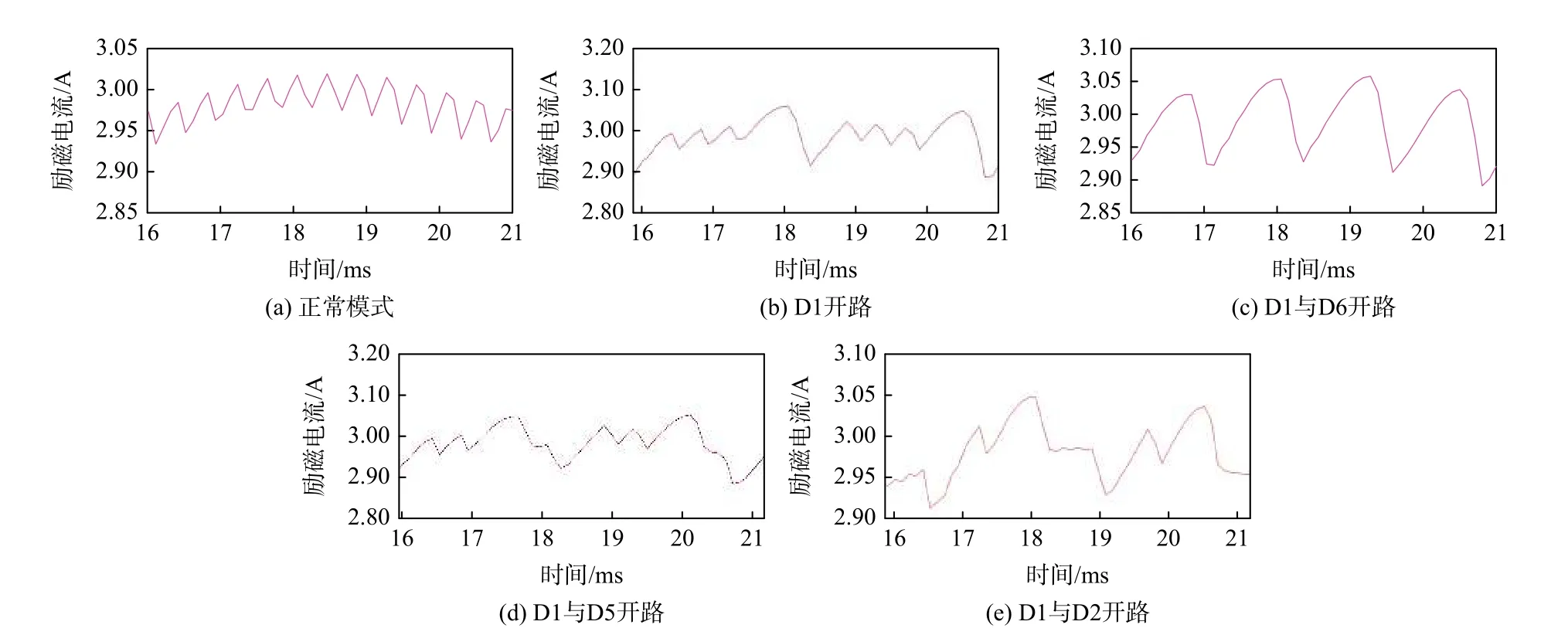
图7 5 类故障状态下的励磁电流信号Fig.7 Excitation current signals under five fault states

3.2 故障特征提取与分类

以旋转整流器D1 二极管开路为例，D1 二极管开路时主励磁机励磁电流经过CEEMD 处理后得到励磁电流的4 个IMF 分量(IMF1～IMF4)，并将其转换成能量熵，将对应的能量熵作为故障特征信号记为E，即

励磁电流4 个IMF 分量的时域特征与对应的能量熵分别如图8 和图9 所示。

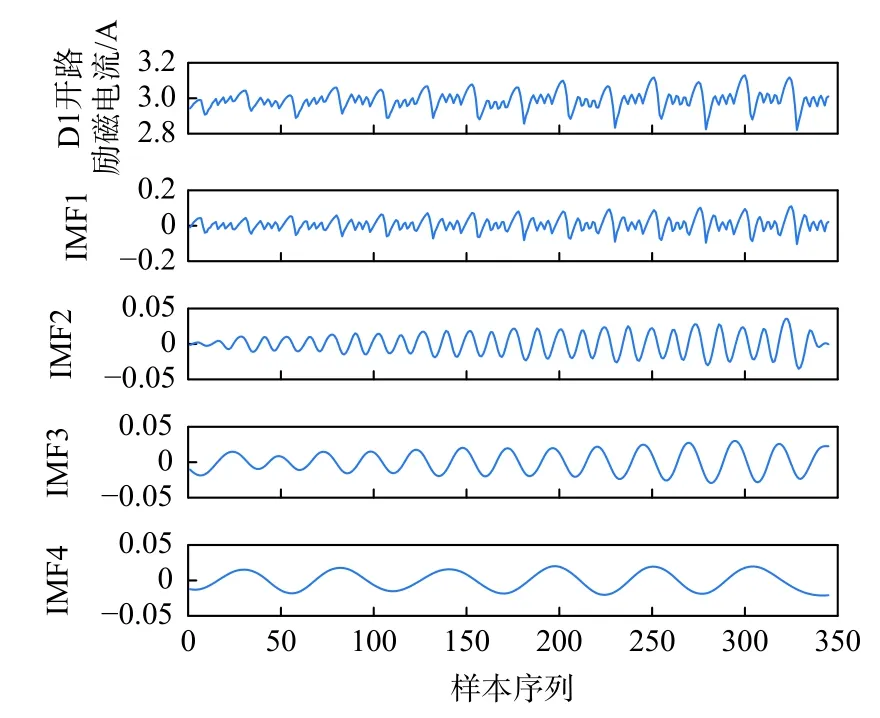
图8 D1 二极管开路时励磁电流IMF 分量的时域图Fig.8 Time domain diagram of IMF component of excitation current in D1 diode open circuit

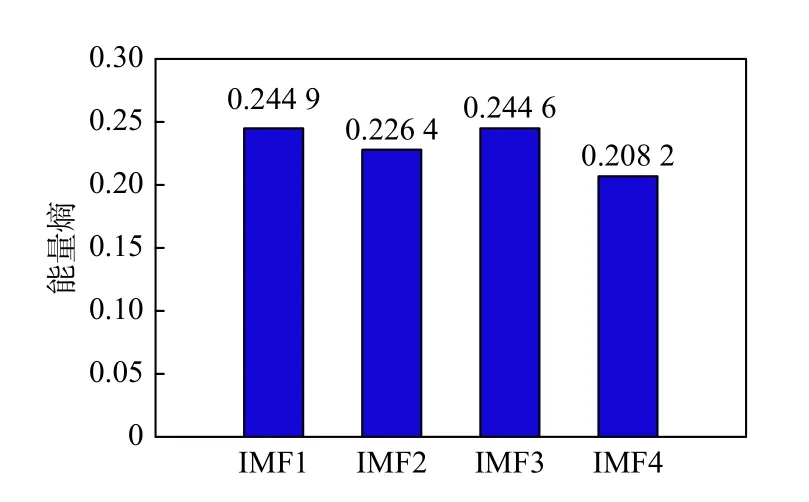
图9 D1 二极管开路时IMF 分量能量熵Fig.9 Energy entropy of IMF component in D1 diode open circuit

重复本节故障特征的提取方法，分别选取一组剩余4 种故障状态的数据进行特征提取，不同故障状态下其能量熵如图10 所示。由图可知，通过CEEMD 对不同故障状态下励磁电流信号处理分析获得的能量熵可以作为故障特征。

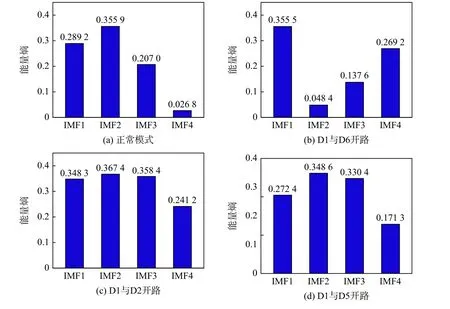
图10 不同故障状态下的能量熵Fig.10 Energy entropy under different fault states

根据提取的故障特征，首先通过本文方法进行故障分类，然后分别和ELM、PSO-ELM、SVM、SSASVM 这4 种故障诊断方法进行对比分析，参数设置具体如下。

1）本文方法、ELM 与PSO-ELM。SSA 与PSO用于对ELM 的权值 ω 和 偏置b进行优化，SSA 的搜索动因子数为40，最大迭代次数为300 次；PSO 的最大迭代次数300 次，粒子数量为40；ELM 隐含层节点数为100，激活函数为‘sig’。

2）SVM 与SSA-SVM。SSA 用于对SVM 的惩罚参数c与RBF 参数g的寻优，设置SVM 的惩罚参数c与RBF 参数g初始值为1 和0.1，svmtrain 训练样本，svmpredict 测试样本，SSA 的参数同上。

3.3 仿真分析

故障特征提取与分类的方法均在MATLAB 2016a 中运行，运行环境Windows10 系统。在混合负载条件下，将空载、1.5 kW 负载、3 kW 负载条件下分别对应的5 类故障状态分别定义标签1～5、6～10 和11～15。基于本文方法的故障诊断结果如图11 所示，故障诊断率达到了100%（750/750），证明了本文方法优异的故障诊断准确性。

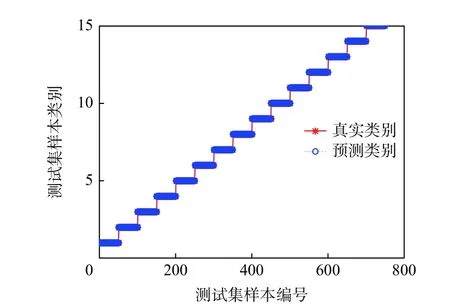
图11 本文方法的故障诊断结果Fig.11 Fault diagnosis results based on proposed method

同时为对比诊断方法的准确性与快速性，依次 在 空 载、1.5 kW 负 载、3 kW 负 载、混 合 负 载4 种条件下对5 种方法对比测试，选取训练时间、测试时间、准确率、诊断方差为性能对比指标，其中训练时间、测试时间、准确率为测试样本的平均值，诊断方差为测试样本的总方差，结果如表3 所示。由表可知，SVM 相对于ELM 其故障诊断准确率更高，但是其故障诊断训练与测试时间明显长于ELM，对2 个分类器分别加入相同寻优算法SSA 改进时，SVM 的训练与测试时间仍长于ELM，这表明SVM 计算机资源占用更大，不利于工程实践。

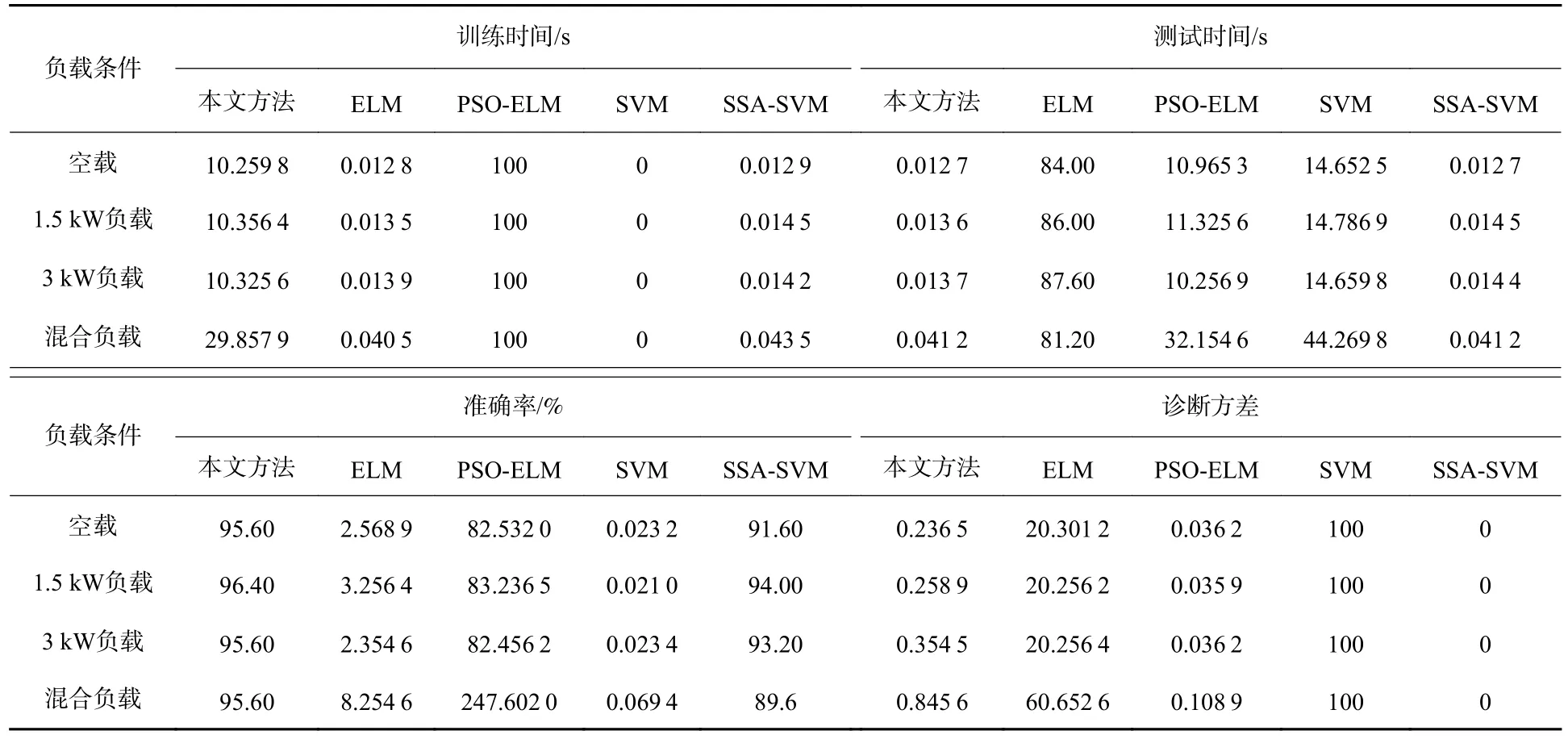
表3 不同负载条件下各分类方法仿真结果性能对比Table 3 Simulation result of performance comparison of different classification methods under different load conditions

ELM 实现开路故障诊断的时间短，但是其故障诊断准确率较低，4 种负载条件下均未到达90%，且诊断方差大，诊断稳定性较低。本文方法相对于ELM 故障诊断准确率有了明显提高，4 种负载条件下均达到了100%，诊断方差均为0。在高准确率的前提下，本文方法相对于基于传统群优化算法PSO-ELM 故障诊断所花费时长较短，诊断准确率与稳定性更高，表明了SSA 寻优算法较好的克服了局部最优问题。以上均表明了本文方法在工程实践中故障诊断的可行性与可靠性。

4 实验分析

4.1 平台简介

因条件所限，实验平台采用改装的三级式同步发电机，将现有的2 个同步电机试验台进行连接，其与仿真的三级式同步发电机组成结构与运行原理完全一致，因此可用其验证本文提出的各种故障诊断方法并比较，平台照片如图12 所示。

该实验平台包括三相异步电动机（拖动高压直流发电机）、高压直流发电机、高压直流电动机（恒定转速驱动励磁电机与主发电机）、启动变阻器（弱磁调速）、交流励磁机（外接电源激磁，励磁频率50 Hz，额定励磁电流2.9 A）、主发电机（额定 转 速3 000 r/min，频 率400 Hz，额 定 输 出 电 压200/115 V）、旋转整流器模块、负载箱、数据采集模块（电流传感器、带模数转换（AD）模块的嵌入式开发板）。

人为设置整流器二极管不同故障模式，通过电机的电刷与滑环将励磁机的电枢电流引出，外接整流器，并将整流桥上的每个二极管串联一个开关，通过控制开关的通断从而达到人为设置二极管开路故障的目的，最终模拟旋转整流器5 类开路故障模式。

4.2 数据采集

实验选择主励磁机励磁电流为采样参数，采样频率10 kHz，在空载、1.5 kW 负载、3 kW 负载条件中，通过霍尔电流传感器分别测量5 类故障状态下励磁电流信号各100 组励磁电流数据(每组数据400 个采样点)，并通过采集板卡将数据发送至PC机，将最终采集的数据混合，得到对应的混合负载样本。

以空载条件下D1 二极管开路为例，通过断开其串联的开关来模拟开路故障，给出实验平台在空载时采集的励磁电流的前400 个采样点波形，如图13 所示。

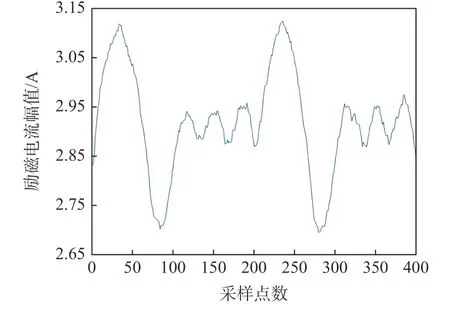
图13 空载条件下D1 二极管开路励磁电流Fig.13 Waveform of D1 diode open circuit excitation current under no load condition

4.3 故障特征提取与诊断

同4.2 结仿真实验步骤一致，首先对励磁电流信号进行CEEMD 分解提取对应能量熵，从而获取故障特征，并按照1∶1 的比例随机划分训练集与测试集，并分别采用5 种方法进行故障诊断，其诊断结果如表4 所示。

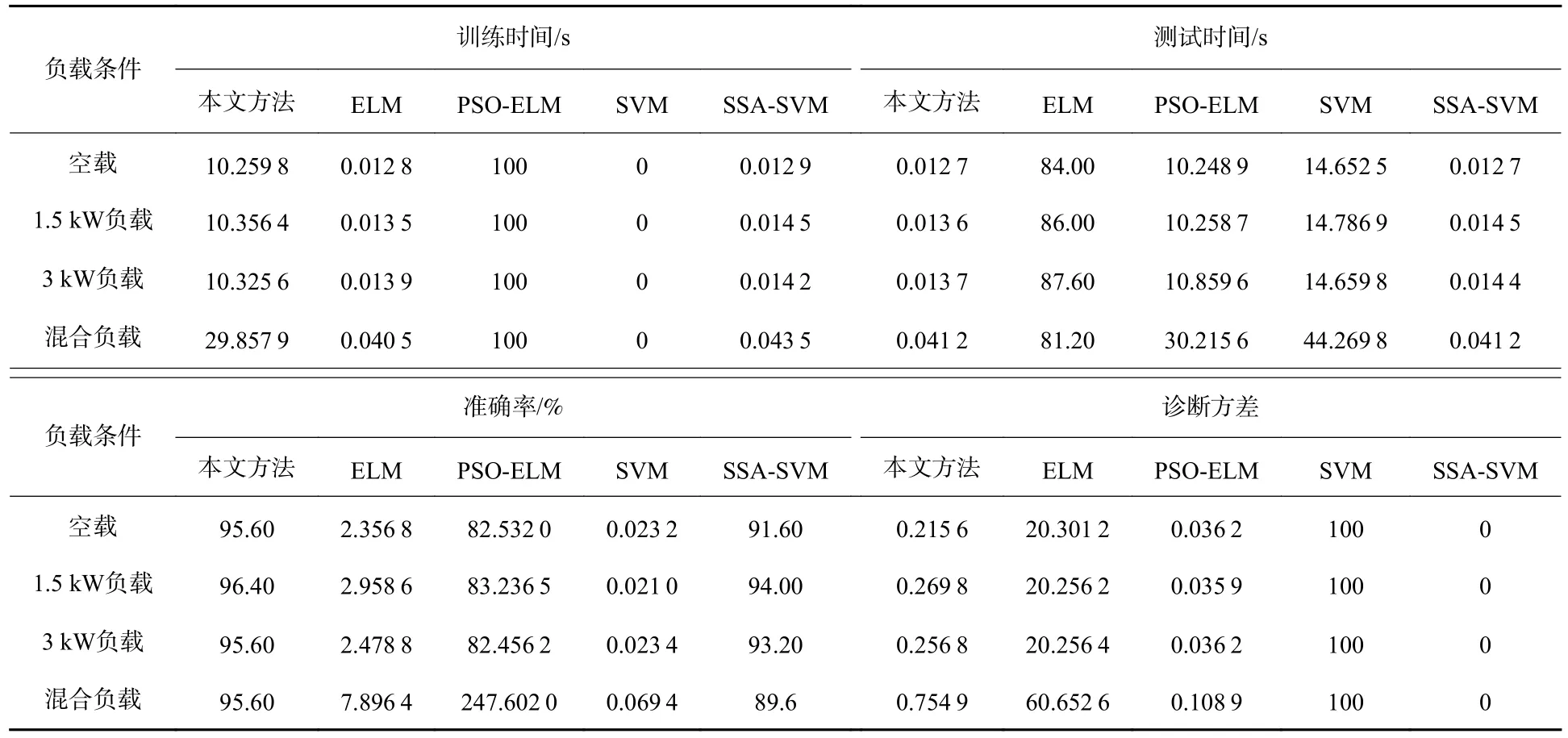
表4 不同负载条件下各分类方法实验结果性能对比Table 4 Experimental results of performance comparison of different classification methods under different load conditions

对比表3 和表4，实验结果与仿真结果接近，表明了基于CEEMD 与本文方法在提取旋转整流器故障特征并进行诊断分类的高效性与可靠性。

5 结 论

1）针对三级式同步电机非线性、复杂性的特点，本文建立了电机有限元模型，有限元模型中旋转整流器开路故障的故障特征与实验验证时的故障特征一致，证明了该模型的有效性。

2）CEEMD 避 免 了EMD 特 征 信 号 提 取 的 缺点，通过选取适当的IMF 分量，可以高效的提取旋转整流器二极管故障时的特征。

3）本文通过引入较强寻优能力的SSA 对ELM的权值与阈值参数优化，在保证ELM 快速诊断的前提下，提高了ELM 故障分类的准确率与诊断的稳定性。

4）本文所提出的故障诊断与分类方法对于非平稳型号具备很好的效果，对于其他故障诊断领域具有较好的借鉴推广意义。