采用花朵授粉算法的等几何边界元形状优化
高翔,王林军,*,刘洋,陈保家,付君健
(1.三峡大学 水电机械设备设计与维护湖北省重点实验室,宜昌 443002;2.三峡大学 机械与动力学院,宜昌 443002)
固体力学中常用的离散方法有有限差分法、有限元法、边界元法、有限体积法、基面力元法[1],岩土力学中常用的离散方法有离散元法和非连续变形分析,流体力学中常用的离散方法有光滑粒子法、移动粒子半隐式法,断裂力学中常用的离散方法有扩展有限元法。在固体力学的形状优化问题中,边界元法仅需要对边界进行离散即可,比其他方法更适用于形状优化问题。
由于CAD 软件采用样条曲线建模,而CAE 软件采用网格建模,样条曲线在离散过程中会产生较大误差,导致CAD 模型和CAE 模型的结果存在一定差异。非均匀有理B 样条(non-uniform relational B-splines, NURBS)曲线灵活多变且精度高,通过等几何分析将CAD 与CAE 这2 种模型无缝连接后,CAE 的精度会有大幅提升[2]。Simpson 等[3]对二维等几何边界元法(isogeometric boundary element method, IGABEM)进行了研究,并与标准边界元法进行对比。Hao 等[4]通过等几何有限元法对结构进行分析,并提出了一种基于增强步长调整 (enhanced step length adjustment,ESLA) 法、二阶可靠性分析法(second order reliability method, SORM)和加速的序列优化与可靠性评估 (stepped-up sequential optimization and reliability assessment,SSORA)法 的 可 靠性优化设计方法。Lian 等[5]提出了一种基于T 样条曲线的形状优化设计方法。Yoon 和Cho[6]通过等几何边界元法对结构进行分析,并对线弹性问题的边界积分方程的敏度进行了推导。Lee 等[7]通过等几何分析、边界积分和水平集法提出了一种形状优化设计方法。Choi 和Cho[8]提出了一种用于等几何形状优化的内部控制点更新方法。Lüdeker 等[9]提出了一种逆均匀化结构的等几何形状优化设计方法。Kang 和Youn[10]提出了基于修剪样条曲面的壳结构形状优化方法。Sun 等[11]通过罚函数法及粒子群算法优化了结构的形状。由于罚函数法的收敛性依赖于罚因子的初始值,亟需寻找一种收敛性优于罚函数法的计算方法。增广乘子法的收敛性不依赖于罚因子的初始值,收敛性比罚函数法更好[12]。
梯度优化算法的收敛速度很快,但容易陷入局部最优解,而智能优化算法的全局寻优能力更好。为了提高智能优化算法的全局寻优能力,很多学者提出了不同的改进方法。其中,文化算法能通过双层进化策略建立的知识库生成新解[13],云模型能通过熵及隶属函数生成服从正态分布的新解[14],分布估计算法(estimation of distribution algorithm,EDA)根据当前若干最优解的均值及标准差生成新解[15],基于Alopex 的进化算法(Alopex-based evolutionary algorithm,AEA)通过Alopex 算法确定当前变量步长的正负号[16],精英反向学习(opposite-based learning ,OBL)策略可生成反向解并逐步缩小搜索范围[17],量子算法通过量子比特编码提高算法的遍历性[18],混沌算法[19]、Lévy 飞行[20]、随机游走[21]这3 种策略均可以提高算法的全局寻优能力。鉴于文献 [13-21]中算法优良的寻优能力,本文将同时采用精英反向学习策略及EDA 改进优化算法。部分学者采用Copula 理论降低样本的相关性,提高算法的全局寻优能力[15],但当相关矩阵非正定时,Copula 理论改进的EDA 不再适用。因此,亟需寻找一种实用性更强的EDA。
鉴于增广乘子法和大规模分布估计算法(large scale EDA,LSEDA)这2 种算法对于优化算法的收敛速度有显著的改进效果,本文提出一种基于花朵授粉算法和等几何边界元的形状优化算法。该算法有如下优点:①采用边界元法对结构分析,并通过NURBS 曲线对结构内部的参数进行插值,避免对整个结构进行离散,仅仅离散结构的边界。②等几何边界元法采用NURBS 函数表示物体的边界,使物体的边界具有精确的几何表示,计算精度更高。③采用增广乘子法对优化模型进行转换,收敛性优于罚函数法。④梯度优化算法的收敛速度较快,但智能优化算法的全局寻优能力更强,可得到性能更好的结构。⑤LSEDA 是一种融合Gauss 分布和Lévy 分布的混合模型[22],不仅可以保证样本集中于最优解附近,而且样本的分布范围更广,全局寻优能力更强。⑥采用精英反向学习策略和LSEDA 改进花朵授粉算法,提高算法的收敛速度和鲁棒性。Ackley 函数的测试结果表明,本文改进的花朵授粉算法寻优能力更强,收敛更快。2 个形状优化算例表明,NURBS 曲线重构的结构边界灵活多样,且仅需要对结构边界离散即可。
1 等几何边界元法
1.1 NURBS 曲线
阶数相同的情况下,B 样条曲线的基函数数量多于贝塞尔(Bézier)样条曲线,计算精度更高[23]。若采用p阶的B 样条曲线,则B 样条曲线的基函数为[24-28]
式中:ξ为节点向量中的一串序列;in为基函数编号。
B 样条曲线上各节点的坐标为
式中:Px(ξ)、Py(ξ)分别为控制点的横、纵坐标。
NURBS 曲线是一种具有非均匀节点向量 Ξ的有理B 样条曲线,且有理B 样条曲线在B 样条曲线的各节点上添加了权重项 ωin。NURBS 曲线的节点向量和节点坐标分别为
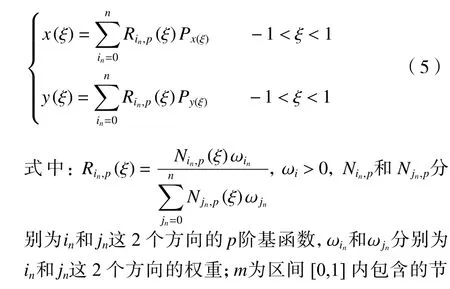
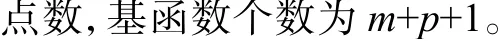
阶数p=1,2,3分别对应线性、二次、三次B 样条曲线,而且B 样条曲线的p−m阶导数连续[23]。
1.2 边界元法
当 源 点x承 受 沿方向i的 载荷ei(x)时 ,场 点x′沿方向j的位移为uj(x′)。根据边界元法的理论,载荷ei(x)与 位移uj(x′)之间的关系式为[29-30]


根据式(13)可求得von Mises 应力[33]为
2 优化算法理论
2.1 增广乘子法
若数学模型的目标函数F(X)有最小值,而且有b个等式约束h(X),则该有约束优化模型可以通过增广乘子法转换为无约束优化模型[12],如下:
式中:r0为 罚因子;λ′为拉格朗日乘子;a为b个等式约束条件h(X)的序号。
2.2 花朵授粉算法
Yang[34]提出了花朵授粉算法。该算法中包括4 种花朵授粉规则:①全局授粉(生物授粉和异花授粉);②局部授粉(非生物授粉和自花授粉);③昆虫授粉;④局部授粉与全局授粉。
规则①和规则③中,采用Lévy 飞行的全局授粉表达式为

Mantegna 算法是一种效率最高的生成服从Lévy分布的伪随机数的算法。该算法生成的步长为

规则④中,当随机数大于指定概率时,采用全局授粉策略;当随机数小于指定概率时,采用局部授粉策略。
为了提高算法的全局搜索能力,本文采用了精英反向学习策略,如下:

式中:Nv为目标函数下F(X)中自变量X的个数;N(0,1)为服从标准正态分布的随机数。
由图1 中的概率密度曲线可知,由于普通EDA通过Gauss 分布生成新解,且新解完全分布于最优解附近,分布范围太小,导致算法的效率较低。然而,LSEDA 采用了Gauss-Lévy 混合模型,新解主要分布于最优解附近,而且分布范围更广,因此LSEDA的效率高于EDA。其中,Cauchy 分布又称柯西分布,是一种特殊的Lévy 分布。
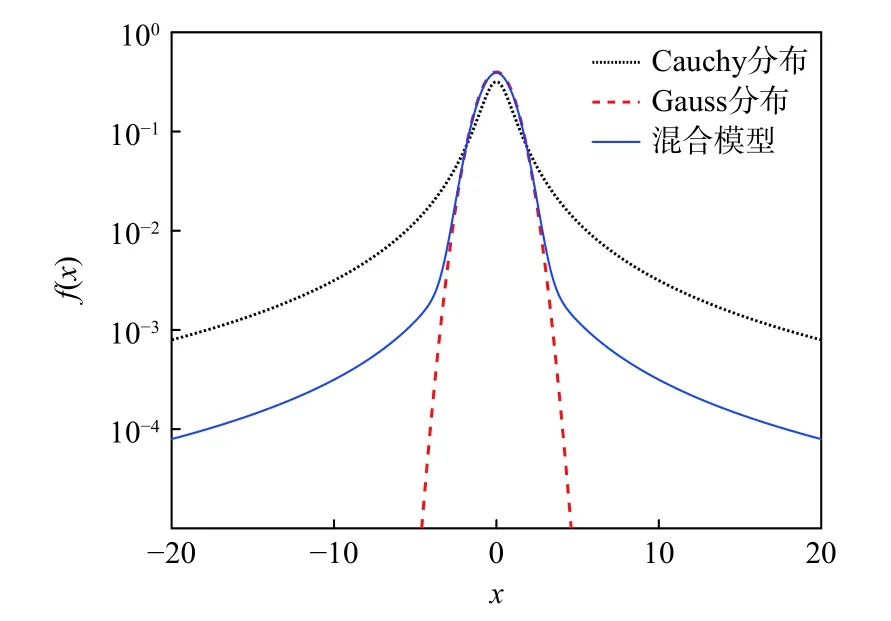
图1 对数坐标系下的Gauss-Lévy 混合模型Fig.1 Gauss-Lévy mixed model in logarithmic coordinate
本文改进后的花朵授粉算法的计算步骤如图2所示,具体步骤如下:
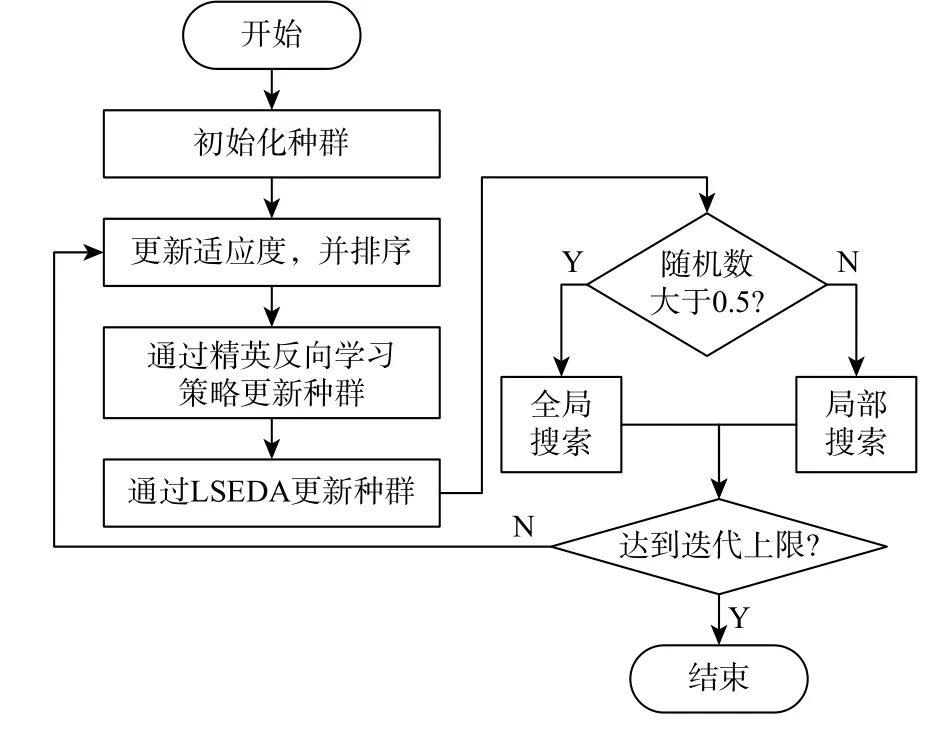
图2 改进的花朵授粉算法流程Fig.2 Flow chart of improved flower pollination algorithm
步骤1初始化种群。
步骤2计算个体对应的适应度,并按升序对个体进行排列。
步骤3当前的最优解采用精英反向学习策略更新。
步骤4最差的25%个体按照LSEDA 更新。通过Gauss-Lévy 混合模型生成的随机数,以及当前25%的最优个体的均值和标准差生成新解,并替换25%的最差个体。
步骤5其他未更新的个体采用基本花朵授粉算法更新。随机数大于0.5 时,全局搜索;随机数小于0.5 时,局部搜索。
步骤6达到迭代上限时,算法终止。否则,算法转步骤2。
现采用Ackley 函数测试本文算法的改进效果。该函数中,变量的取值范围为(−32.768,32.768),且函数的最小值0 所在位置为(0, 0, ···, 0)。通常,Ackley 函数的各参数为:a0=20,b0=0.2,c0=2π,d0为 变量X的维度,且Ackley 函数的表达式为
设花朵授粉算法的种群数量为20 个,迭代上限为200 步。同时采用精英反向学习策略和LSEDA 这2 种算法的花朵授粉算法与基本花朵授粉算法的迭代过程如图3 所示。
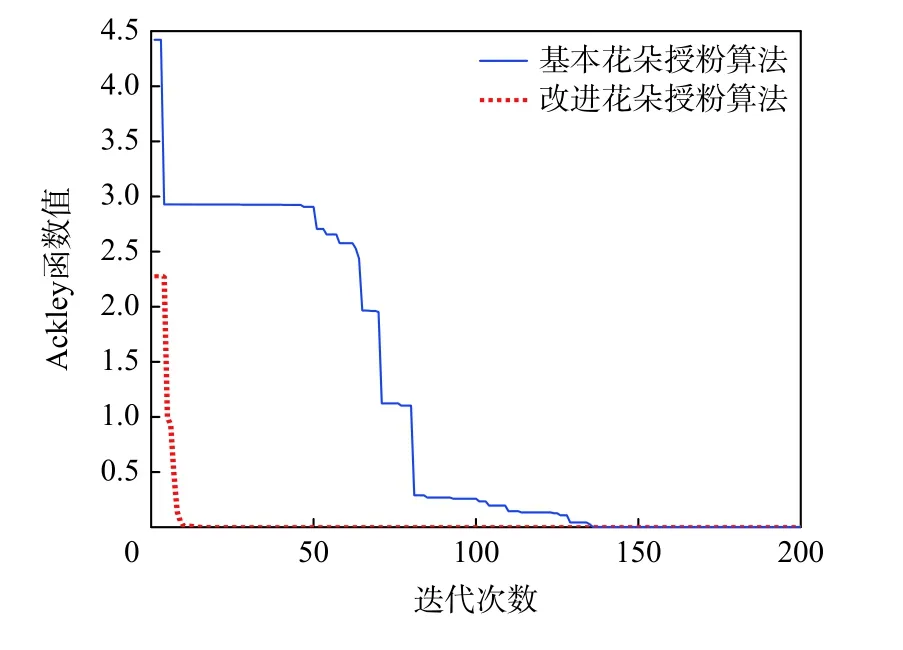
图3 两种花朵授粉算法的对比Fig.3 Comparation of two kinds of flower pollination algorithms
由图3 可知,本文算法在第14 步收敛,最优解为(−0.294 8, −0.100 1),最小值为8.881 8×10−16;而基本花朵授粉算法在136 步收敛,最优解为(−0.447 0,−0.777 7),最小值为0.001 4。因此,本文算法寻优能力更强,且将采用本文算法优化等几何边界元模型,以实现结构的形状优化设计。
3 基于等几何边界元法的形状优化
本文通过精英反向学习策略和LSEDA 这2 种算法改进了花朵授粉算法,并将该算法用于优化等几何边界元模型中的控制点,提出一种新的形状优化设计算法。该算法的计算流程如图4 所示。

图4 本文算法流程Fig.4 Flowchart of the proposed algorithm
3.1 位移最小化的形状优化
结构左端面上方3 个控制点固定,右端面下方3 个控制点承受载荷,横向载荷50 N,纵向载荷200 N。弹性模量为 2×105MPa,泊松比为0.3。初始结构的参数设置如表1 所示,结构示意图如图5(a)所示,初始形状如图5(b)所示,NURBS 基函数如图5(c)所示。

表1 位移算例的控制点及节点向量Table 1 Control points and knot vectors for displacement example
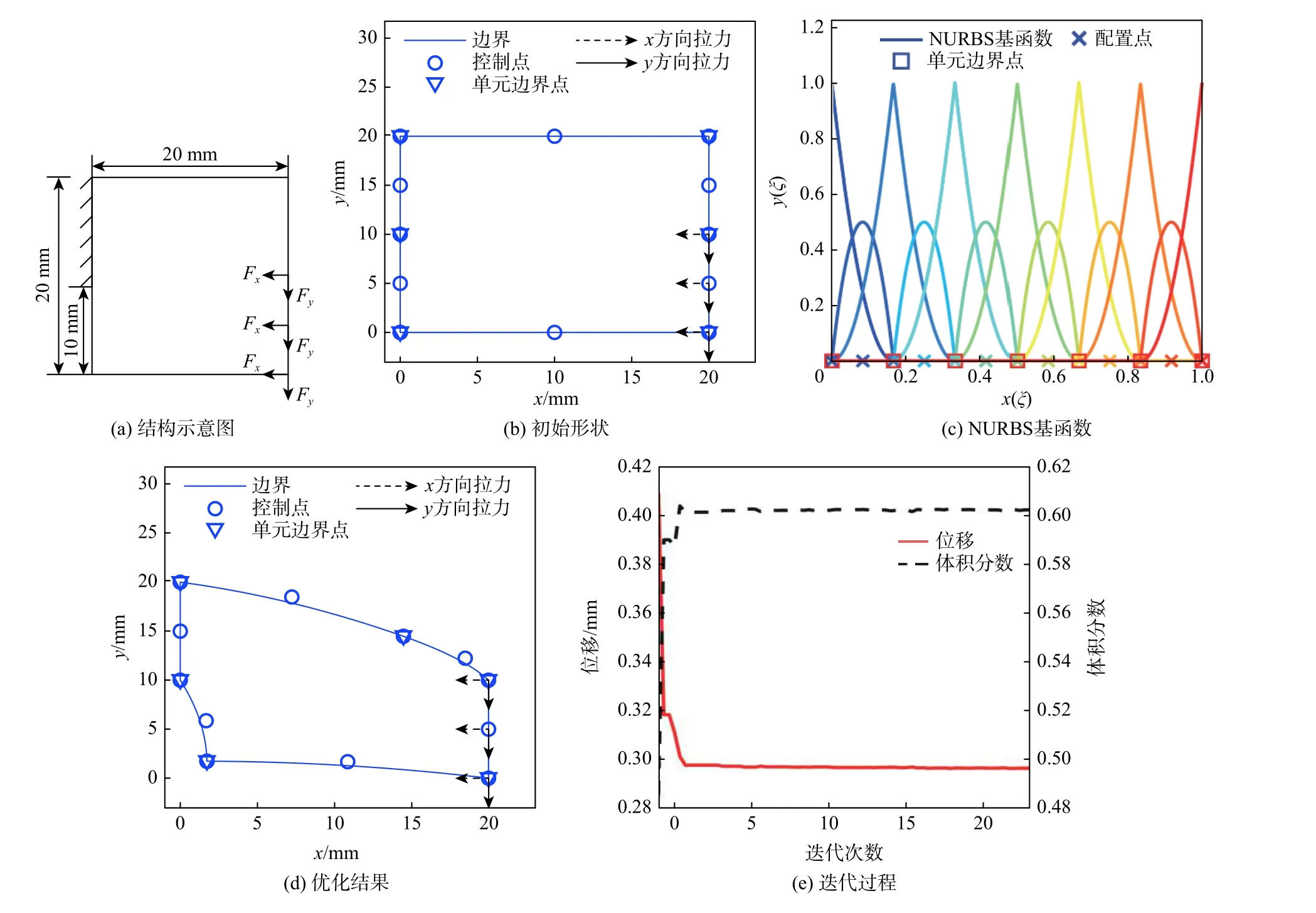
图5 位移最小化Fig.5 Minimization of displacement
由式(4)可知,表1 中 Ξ对应的NURBS 曲线阶数p为2 阶,[0,1]内包含的节点数m为10,因此基函数个数为10+2+1=13 个。式(5)为NURBS 基函数的计算式。
现在需要将结构的面积减少至60%,并且最小化每个控制点的最大位移。设罚因子为 1×102,拉格朗日乘子的初始值为0,且每迭代一次,拉格朗日乘子增加 1×10−6,花朵授粉算法所得结果如图5(d)所示,迭代过程如图5(e)所示。由图5(e)可知,花朵授粉算法在10 步以内收敛,收敛性非常好。70 次迭代后,由图5(c)中的NURBS 基函数构建的结构如图5(d)所示,且结构中的各控制点的最大位移下降至0.297 2 mm,体积分数为0.602 2。
3.2 应力最小化的形状优化
结构上端面承受纵向载荷2 000 N,下端面两端固定,弹性模量为 2×105MPa,泊松比为0.3。初始结构的参数设置见表2,结构示意图见图6(a),初始结构见图6(b),NURBS 基函数如图6(c)所示。现需要将结构的面积减少,同时最小化每个控制点的最大应力。设罚因子为 1×104,拉格朗日乘子的初始值为0,且每迭代一次,拉格朗日乘子增加 1×10−5。由图6(e)可知,花朵授粉算法在20 次迭代以内,曲线趋于平缓,收敛性较好。由图6(c)构建的结果见图6(d)。

表2 应力算力的控制点及节点向量Table 2 Control points and knot vectors for stress example
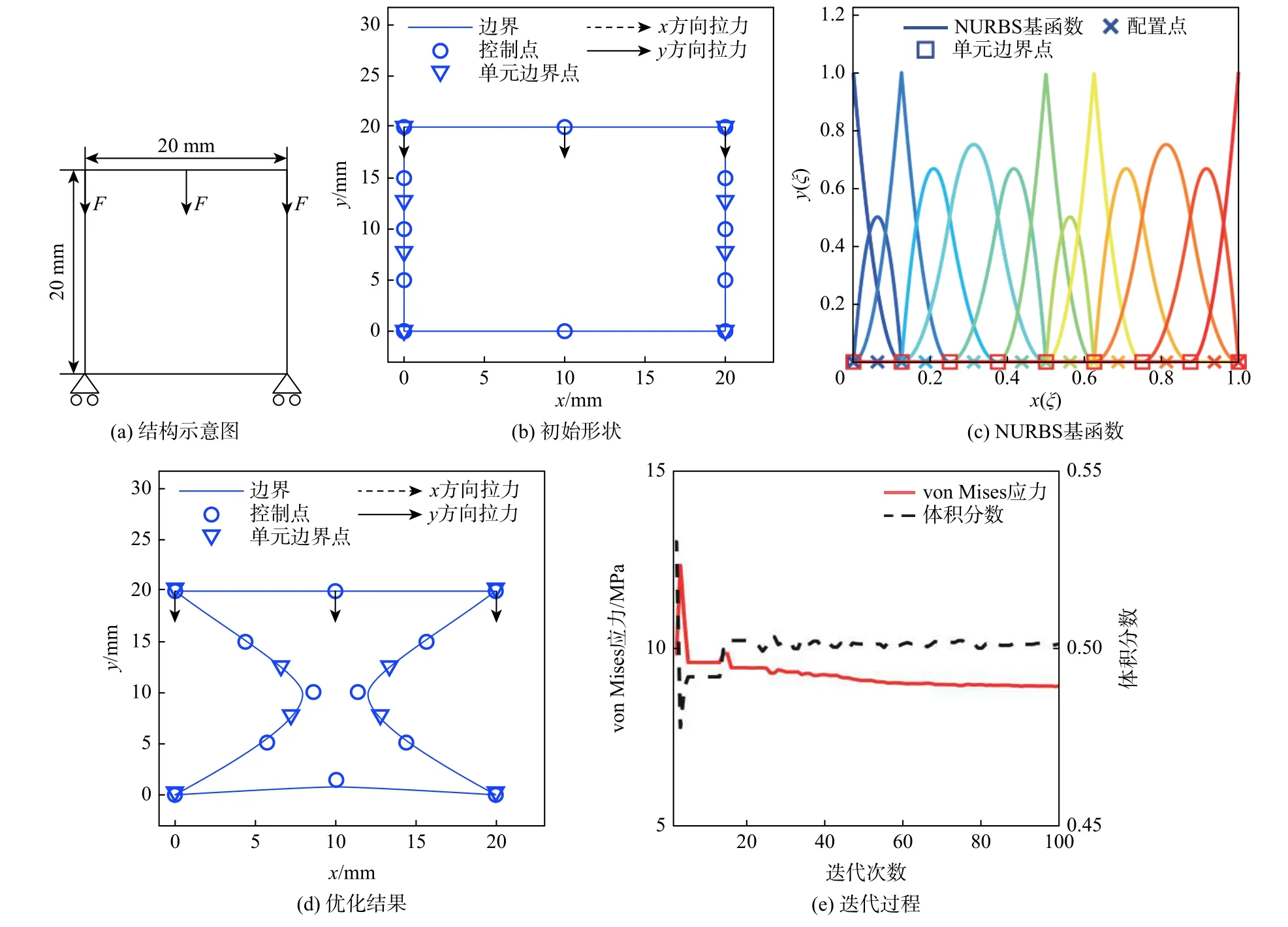
图6 应力最小化Fig.6 Minimization of stress
4 结 论
通过精英反向学习策略及LSEDA 对花朵授粉算法进行改进,并用于优化等几何边界元模型的形状,算例结果表明:
1)通过精英反向学习策略及LSEDA 这2 种算法改进了花朵授粉算法,且Ackley 函数的测试结果表明,本文算法寻优能力更强。
2)通过本文算法求得的控制点坐标重构了NURBS 曲线,而且该NURBS 曲线非常光滑,能精确地表示结构边界。
3)结构示意图中,“单元边界点”均位于结构的边界,而结构的其余节点均通过NURBS 基函数及权值进行插值求得,因此“配置点”不一定位于结构的边界上。

