Herbst 机动中的摇滚运动试验研究

李乾，王延奎，贾玉红

(北京航空航天大学 航空科学与工程学院，北京 100191)

过失速机动能力是新型战斗机的性能指标之一，其中，典型机动是赫布斯特（Herbst）机动。能否完成Herbst 机动已逐渐成为检验战斗机过失速机动能力是否优良的手段。Herbst 机动，又被称为钩子机动（J-turn），主要特征是小转弯半径和快速改变指向。1993 年，X-31A[1-5]成功实现了Herbst 机动。机动过程为：先高速平飞进入机动准备阶段，经历约2 s 的迎角拉起，速度降低进入过失速迎角区域，再使飞机绕速度矢量轴旋转约180°，此时飞行速度约45 m/s，再经迎角快速下俯退出过失速迎角区域，加速平飞退出机动。Herbst 机动能够实现机头指向改变180°，转弯半径475 ft（约145 m，1 ft（英尺）=0.304 8 m），远小于常规转弯的2 500 ft（约762 m），小半径的急转弯机动性可极大提高近距格斗的攻击能力及作战效率，具有较强的实战意义，这在当时是具有划时代意义的。为纪念提出过失速机动概念的Herbst[3-4]，美国国家航空航天局(NASA)将该机动命名为Herbst机动。

为了实现Herbst 机动，战斗机需要具备出色的大迎角气动性能，先进飞行控制系统和推力矢量技术等条件。在大迎角飞行中，战斗机将出现复杂的背涡流动及其诱导的机翼摇滚运动，威胁飞行安全。考虑到隐身性能，现代战斗机采用了尖侧缘机身，如F-22、F-35 等，因此，研究尖侧缘机身布局在Herbst 机动中的摇滚运动，利于理解战斗机在Herbst机动中的气动/运动耦合现象。

前人针对翼身组合体的摇滚运动开展了大量的研究。一方面，重点是固定迎角（静态迎角、俯仰角或者支杆支撑角）下的摇滚运动形态。这是因为迎角是摇滚运动的关键参数，如常关注的摇滚运动起始迎角，迎角运动图谱等。研究发现[6-8]，翼身组合体在大迎角摇滚运动的产生原因是机身前体涡的诱导，机翼只起到作用面的作用。相较机身形状（尖头细长体，钝头体，尖侧缘机身等）对摇滚运动的影响[6]，发现除尖侧缘机身外，其他机身前体均出现明显的摇滚运动。但是，Shi 等[9-10]通过试验发现，带尖侧缘机身的组合体在大迎角也会出现了摇滚运动，且更加复杂，表现出了大振幅的混沌摇滚[9]和“反极限环”摇滚[10]，运动形态与尖侧缘机身非对称涡和机翼流动的相互作用有关。另一方面，翼身组合体摇滚还关注了头尖部扰动[11-13]和雷诺数[13-15]对组合体摇滚运动的影响。这是因为组合体中机身为细长旋成体，而旋成体机身非对称涡的形态受头尖部扰动和雷诺数的影响，头尖部扰动能够改变旋成体机身非对称涡的涡型[16]，而雷诺数能够影响非对称涡供给剪切层的分离方式。对于尖侧缘机身，Tian 等[17]试验研究了尖侧缘机身的非对称流动，尖侧缘机身非对称流动的雷诺数效应较弱，可能是因为主分离线固定在侧缘上，基本不受雷诺数影响。Shi 等[18]试验发现，尖侧缘机身的非对称涡仅在零滚转角时受头尖部扰动主控，但在非零滚转角受侧缘的侧滑角主控，因此，尖侧缘机身布局的摇滚运动形态受雷诺数和头尖部扰动的影响较弱，主要受迎角（或俯仰角）的影响。

目前，关于俯仰拉起或更复杂机动中的摇滚运动研究较少。Khan 等[19]研究了俯仰振荡对80°后掠三角翼机翼摇滚的影响，发现振荡频率影响摇滚运动的形态。Tregidgo 等[20]研究了俯仰周期振荡对矩形翼自由摇滚运动频率的锁定现象，徐思文等[21]针对细长旋成体和小后掠机翼构成的组合体模型，通过试验研究了迎角拉起中的摇滚运动，发现快速拉起时出现与固定迎角截然不同的类正弦摇滚运动，该运动主要是前体非对称涡随迎角的演化导致的。关于模拟Herbst 机动的风洞试验装置公开文献较少，Geng 等[22]研制了可模拟Herbst 机动的五自由度试验机构，得到了旋成体机身翼身组合体俯仰振荡和滚转振荡的非定常气动力及固定俯仰角下的摇滚运动，但没有涉及在Herbst 机动中的摇滚运动形态。

综上，尖侧缘机身布局固定俯仰角下会出现摇滚运动，那么在Herbst 机动中，机身非对称流动将随着模型运动而出现迟滞现象，是否仍出现摇滚运动，以及运动形态如何，针对这些问题，本文研制了模拟Herbst 机动的风洞试验装置，设计了尖侧缘机身组合体模型，研究了布局模型在Herbst 机动中的摇滚运动形态，揭示了摇滚运动产生的主要阶段，研究了Herbst 机动的运动参数对摇滚运动的影响特性，初步讨论了雷诺数和拉起速度对俯仰拉起摇滚运动的影响规律，得到了拉起减缩频率作为摇滚运动相似参数的适用范围，为进一步认识机动中摇滚运动和发展相应的流动控制技术奠定了基础。

1 试验模型、设备及数据处理

模型由尖侧缘机身（或脊型机身）和中等后掠梯形机翼组成，如图1 所示。机身长680 mm，后体参考宽度D= 80 mm，后体高度70 mm。机身截面轮廓沿体轴方向相似，轮廓的上下段由抛物线定义。以x/D= −3.0 截面为界，机身可分为前体和后体，前体侧缘线为曲线，后体侧缘线为直线。平板机翼翼根前缘点位于x/D= −4.5 的位置，机翼平面形状为梯形，前缘后掠角48°，后缘前掠15°，翼展340 mm。机翼前缘和后缘下表面倒角45°。机身材料为铝，机翼材料为有机玻璃。绕体轴的转动惯量通过三维建模软件计算约为0.004 kg·m2。

图1 试验模型Fig.1 Test model

试验在北京航空航天大学D4 低速风洞完成，来流湍流度为0.08%。试验采用开口试验段，试验段截面尺寸为1.5 m × 1.5 m，长度为2.5 m。试验风速为35 m/s，基于机身后体参考宽度的雷诺数ReD为1.87×105。

本文主要试验方法为自由摇滚试验，通过安装在Herbst 机动试验装置上的自由摇滚支杆得到机动中模型的摇滚运动。图2 为自由摇滚支杆示意图，自由摇滚支杆由转子、联轴节、电磁闸、光电编码器和外壳构成。模型与自由摇滚支杆的转子连接，模型的运动滚转角数据通过编码器记录，编码器12 bit 的角度分辨率为0.088°。电磁闸根据实际需要采用手动和程序内部控制。自由摇滚试验流程为：将模型运动到待测俯仰角，风速稳定后，通过控制程序释放电磁闸，编码器记录模型的滚转角运动时间历程曲线，得到该俯仰角下模型的摇滚运动形态。

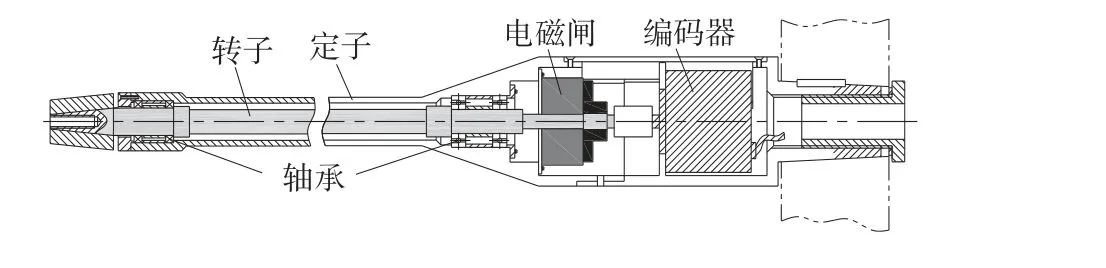
图2 自由摇滚支杆示意图Fig.2 Diagram of free-to-roll rig

摇滚运动的平衡位置和振幅的提取忽略了0～5 s 的运动建立过程，使用5～20 s 的滚转角时间历程曲线来计算。平衡位置 ϕeq取滚转角的平均值，摇滚振幅 ϕam为滚转角的均方差。在求滚转角速度和角加速度之前进行滤波处理，这是因为高采集频率128 Hz 加上有限的滚转角分辨率0.088°，使得小角速度出现连续相同值，等同于高频噪声，采用有限冲击响应的10 Hz 低通数字滤波器进行滤波。滤波后，利用四点中心差分方法求导得到摇滚运动的角速度和角加速度，通过快速傅里叶变换得到了摇滚运动的频域特性。

2 Herbst 机动运动风洞试验装置

2.1 设计方案

X-31A 验证机的Herbst 机动飞行试验表明[2]，其研究共有4 个里程碑阶段：①保持迎角70°平稳飞行；②在迎角70°绕速度矢量轴旋转；③动态快速拉起至迎角70°；④完成最小转弯半径和最大转弯速率条件下的机头指向180°转向。可以看出，实现Herbst 机动运动的关键是：从巡航状态到过失速状态的俯仰拉起运动和绕速度矢量轴的圆锥运动。因此，试验装置的设计方案为通过组合俯仰拉起和圆锥运动来模拟。考虑到经济性，以北京航空航天大学D4 风洞原有的俯仰拉起机构为基础进行改造，在原来拉起机构的末端即支杆连接端改造成圆锥运动执行机构，圆锥运动执行机构末端设计支杆连接端。重新配置电机和控制程序，最终实现Herbst 机动运动的模拟。图3 为 Herbst 机动风洞试验装置实物图。配重保证模型安装后的运动转动轴与机械转动轴同轴。为了减小旋转装置对气动力的干扰，引入了整流设计。为了验证Herbst 试验装置流场模拟的正确性，在北京航空航天大学D4风洞原有常规尾撑装置和Herbst 试验装置开展了模型的静态气动力测量和固定迎角下摇滚运动试验，结果如图4 所示。可知，Herbst 试验装置测得的气动力和摇滚运动形态与原有常规尾撑装置测得结果基本吻合，误差较小。

图3 Herbst 机动风洞试验装置实物图Fig.3 Physical diagram of Herbst maneuver wind-tunnel test device

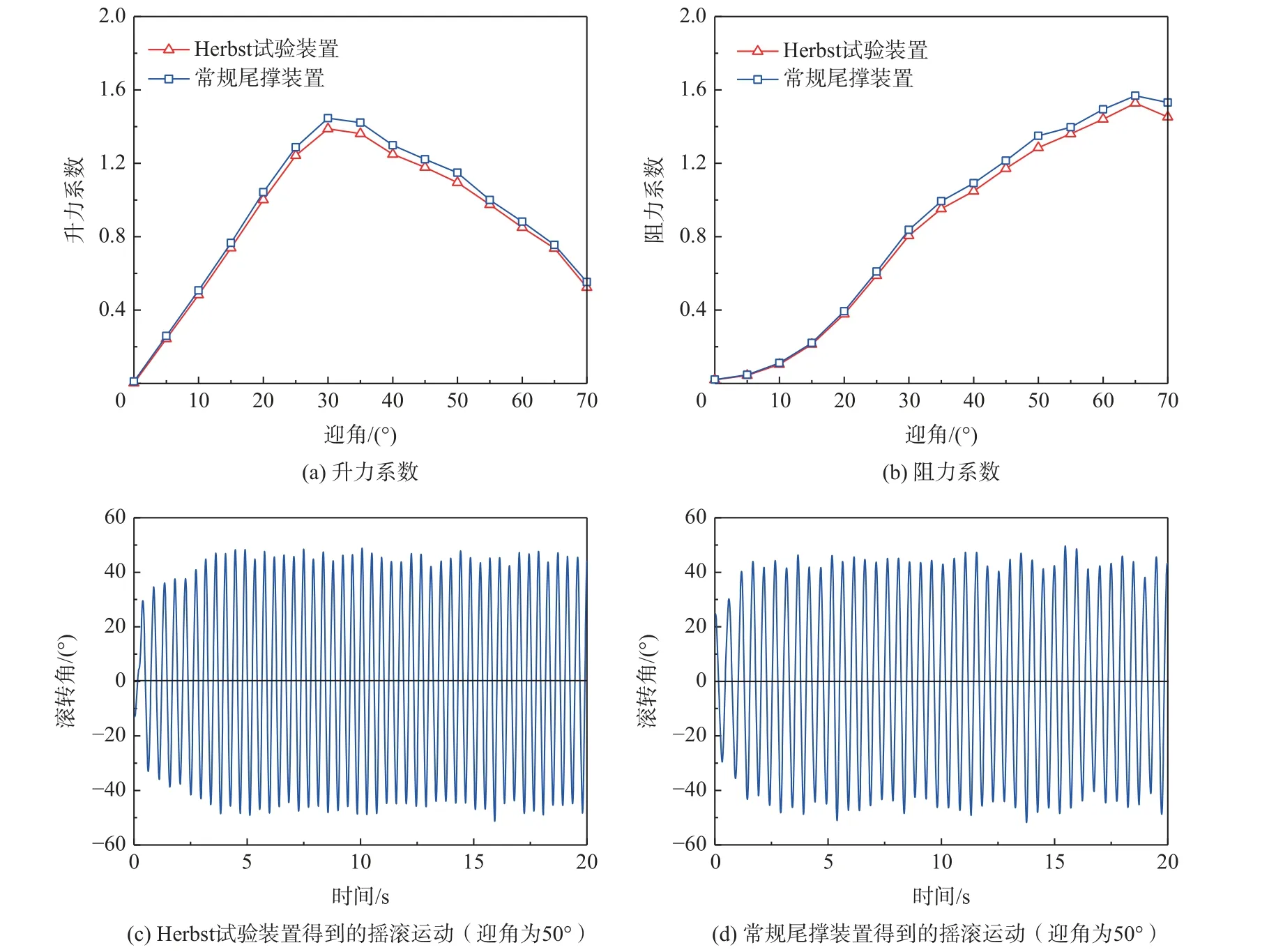
图4 Herbst 试验装置与常规尾撑装置的试验结果Fig.4 Test results of Herbst test device and conventional tail-sting support device

2.2 运动参数

模型俯仰拉起结束后进行圆锥运动，拉起运动和圆锥运动相对独立，其运动参数相对独立，符合Herbst 机动的主要特征。俯仰角 θ为机体轴与水平面之间的夹角，当头部上仰为正，在试验中，等于自由摇滚支杆的支撑角。除Herbst 机动运动控制所必需的参数外，需要重点解释电磁闸释放角度θBR。为了简化问题，俯仰拉起和绕速度矢量的圆锥运动的速率均为常值，没有考虑变速情况。电磁闸释放角度设置为匀速拉起过程中的俯仰角。试验中设置 θBR的角度，主要基于2 方面的考虑：①固定俯仰角的自由摇滚试验结果[23]，俯仰角小于20°时，模型稳定在零滚转角位置，不出现摇滚运动，只有当俯仰角大于20°之后，才开始出现横向运动；②受驱动电机的限制，从俯仰角0°需要前置加速段才能到达指定的匀速拉起速度。在不改变电机的条件下，所需拉起速度越大，加速段越长。当采用最高拉起速度70 (°)/s 时，实测加速段长度不小于20°，因此电磁闸释放角度 θBR一般设置为20°，此时也保证释放处在匀速拉起段。

图5 为模拟Herbst 机动中俯仰角 θ和圆锥运动角 ϕc的 时间历程。ϕc为模型绕速度矢量轴的旋转角度，以拉起结束时为圆锥运动的起始角度，此时的俯仰角数值上等于几何上的圆锥角，圆锥运动的旋转方向以逆来流方向逆时针为正。θSP和 θEP分别为匀速拉起运动起始和结束俯仰角，ϕSC和 ϕEC分别为匀速圆锥运动起始和结束角度，ΛCA为圆锥角，即拉起结束时模型体轴与速度轴夹角，ωp为拉起速度，ωc为圆锥运动速度。时间历程曲线分为3 个阶段：拉起阶段、圆锥运动阶段和下俯阶段。下俯阶段是拉起阶段的逆向过程，运动控制方式相似，下俯阶段采用了与拉起阶段相同的运动参数。

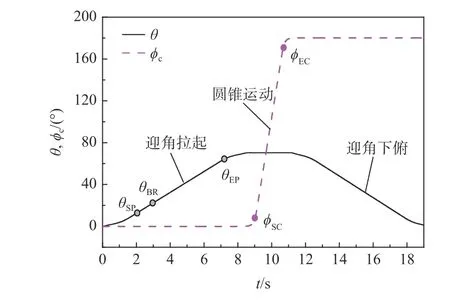
图5 Herbst 机动中俯仰角 θ 和圆锥运动角 ϕc 的时间历程（ΛCA =70°，ωp =10（°）/s，ω c=100（°）/s）Fig.5 Time histories of pitch angle θ and motion angle of coning ϕc in Herbst maneuver ( ΛCA =70°，ωp=10（°）/s，ωc=100（°）/s)

图6 为模拟Herbst 机动的主要过程。试验准备阶段，根据试验状态所需选定圆锥角 ΛCA，调整弧形滑轨安装，根据模型重量调整配重，该角度等于拉起结束的模型俯仰角，先安装弧形滑轨。调整模型的初始俯仰角为0°，初始滚转角为0°，如图6(a)所示。设定好拉起速度和圆锥运动速度，模型按照以下步骤完成Herbst 机动。

图6 Herbst 机动的主要过程Fig.6 Primary processes of Herbst maneuver

步骤 1拉起运动电机工作，驱动模型从俯仰角0°加速到匀速拉起起始角度 θSP，然后以拉起速度ωp驱 动模型运动至匀速拉起结束角度 θEP，再减速拉起运动到最大拉起角度，此时模型体轴相对来流夹角为指定圆锥角，如图6(b)所示。

步骤 2圆锥运动电机开始工作，与拉起运动的控制类似，驱动模型经历加速到匀速圆锥运动起始角度 ϕSC，以圆锥运动速度 ωc运动到匀速圆锥运动结束角度 ϕEC，再减速到达最大圆锥运动角度180°，此时实现模型绕速度矢量旋转180°，如图6(c)所示。

步骤 3拉起运动电机工作，驱动模型以拉起运动相同规律完成加速—匀速—减速，模型俯仰角由70°下俯至0°，如图6(d)所示，机动结束。

2.3 典型试验状态

典型试验工况来源于X-31A 完成Herbst 机动的试验结果：快速拉起至最大迎角（俯仰角）70°，之后绕速度轴旋转180°，过程中飞机速度从0.1Ma到0.4Ma，耗时8～12 s。典型状态为最大俯仰角70°和圆锥运动角180°，状态由圆锥角命名为Herbst70，参数设置如表1 所示，表中还给出了Herbst50 机动状态的参数设置。试验中选择的俯仰角拉起速度范围为1～50 (°)/s，圆锥运动速度为5 (°)/s 和100 (°)/s。

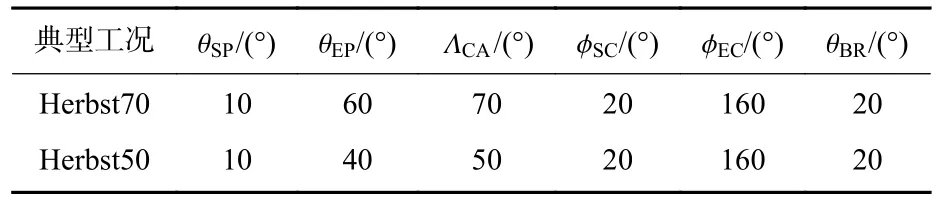
表1 Herbst 机动的典型试验工况Table 1 Typical test cases of Herbst maneuver

3 Herbst 机动中的摇滚运动

3.1 慢速Herbst 机动中的摇滚运动

图7 为慢速Herbst70 机动过程中模型的摇滚运动。拉起速度 ωp= 1 (°)/s，圆锥运动速度 ωc= 5 (°)/s。为了更清晰地讨论慢速Herbst 机动中的摇滚运动演化规律，将摇滚运动按照时间顺序的相图分段展示，图8 为不同时间段摇滚运动的相图，图中圆点表示该时间段运动的起点，除起始外，该起点为上一摇滚运动的终点，尖侧缘机身布局在Herbst 机动过程中出现了较明显的机翼摇滚运动，下面将分3 个阶段描述摇滚运动的形态。

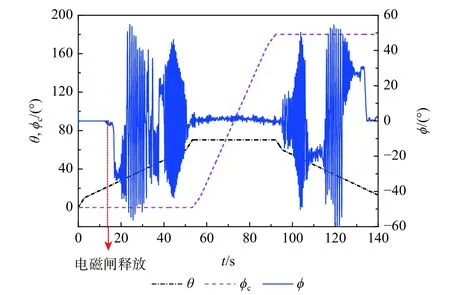
图7 慢速Herbst70 机动中的摇滚运动（ωp =1（°）/s，ωc=5（°）/s）Fig.7 Roll oscillations in slow Herbst70 maneuver（ωp = 1（°）/s，ω c=5（°）/s）

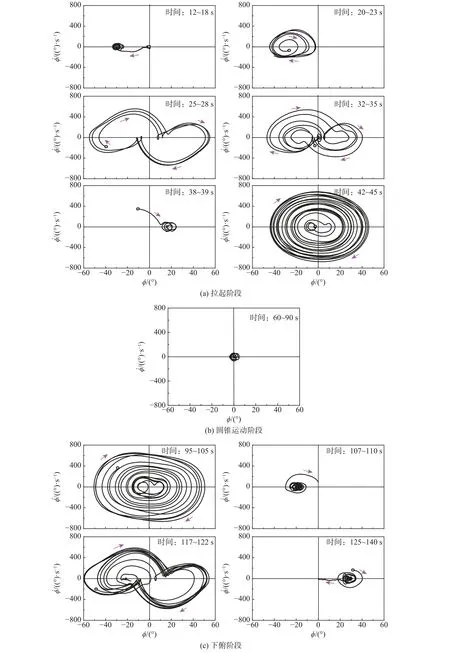
图8 慢速Herbst70 机动中摇滚运动的相图Fig.8 Phase plots of roll oscillations in slow Herbst70 maneuver

拉起运动阶段，相图如图8(a)所示，释放电磁闸后，模型经历短暂停留在滚转角 ϕ=0◦后，12～18 s时出现负向偏离，并在 ϕ=−30◦附近保持平衡，相图轨迹收敛与一点，运动形式为微振；20～23 s 时运动振幅逐渐变大，相图轨迹能够收敛到固定轨道上，运动形式为单侧极限环振荡；25～28 s 时，随俯仰角继续增加，在负侧的运动振幅大于负侧运动的平衡位置，模型能够跨越过零滚转角，到达正侧摇滚，正侧运动返程再次跨越零滚转角，回到负侧，周而复始，模型相图轨迹能够收敛到固定轨道，此时运动类型不再是单侧运动，而是以平衡位置 ϕ=0◦，振幅约60°的极限环运动；随着俯仰角继续增加，32～35 s 时运动振幅逐渐减小，运动中出现不能越过零滚转角的单侧振荡，且每次运动越过或不越过零滚转角表现出随机性，模型运动形式为混沌摇滚；俯仰角继续增加，38～39 s 时模型运动振幅突然大幅减小，回到单侧微振；增加俯仰角，42～45 s时模型出现了大振幅的摇滚运动。随俯仰角继续增加，振幅减小，摇滚运动逐渐消失，模型稳定在零滚转角附近。

圆锥运动阶段，相图如图8(b)所示，模型延续拉起结束时的运动状态，稳定在零滚转角附近。

下俯运动阶段，相图如图8(c)所示，该相图与拉起阶段的图8(a)类似。下俯与拉起相反，俯仰角由大变小。随俯仰角从70°减小，模型从在零滚转角附近的微振变为95～105 s 时绕零滚转角的大振幅摇滚，与拉起阶段不同，摇滚运动振幅随俯仰角变小而变小，相图由外环逐渐绕到内环；随俯仰角继续减小，107～110 s 大振幅摇滚运动变为一侧微振，轨迹收敛到负侧滚转角 ϕ=−20◦附近；俯仰角继续减小，117～122 s 模型的运动形式变为混沌摇滚；俯仰角再次减小，125～140 s 时轨迹从绕正滚转角的极限环，先衰减到正滚转角，之后回到零滚转角。

3.2 快速Herbst 机动中的摇滚运动

图9 为快速Herbst70 机动过程中的摇滚运动，不同时间段的运动相图如图10 所示，图中圆点为该时间段运动的起点。拉起速度 ωp= 50 (°)/s，圆锥运动速度 ωc= 100 (°)/s。

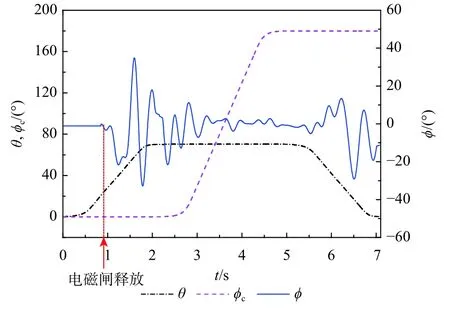
图9 快速Herbst70 机动中的摇滚运动（ω p = 50（°）/s，ωc=100（°）/s）Fig.9 Roll oscillations in fast Herbst70 maneuver（ω p = 50（°）/s，ωc=100（°）/s）

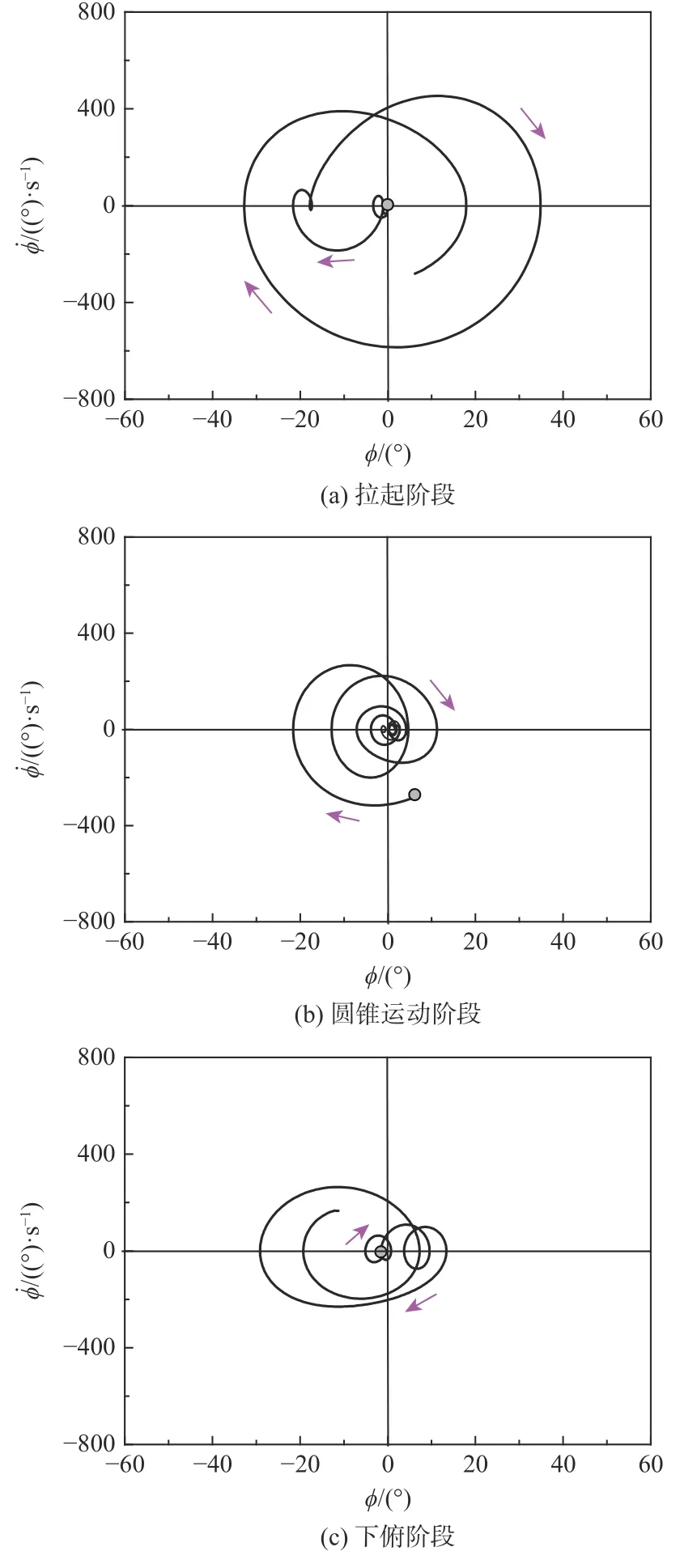
图10 快速Herbst70 机动中摇滚运动的相图Fig.10 Phase plots of roll oscillations in fast Herbst70 maneuver

拉起阶段，释放电磁闸后，模型负向偏到ϕ=−20◦附近，之后正向运动到达ϕ =38◦又开始负向运动，经过1～2 个周期，最终在 ϕ =10◦负向运动时，拉起阶段结束，如图10(a)所示。拉起中模型形成约2 个周期的摇滚运动，相图轨迹为减幅的轨道，运动形式表现为减幅类正弦运动。圆锥运动阶段，相图如图10(b)所示，运动振幅减小到零，相图轨迹收敛到零滚转角。下俯阶段，相图如图10(c)所示，模型从零滚转角偏向正滚转角 ϕ=10◦微振，负向运动到达 ϕ=−30◦反向，经历一个周期的减幅类正弦运动停止。

对比慢速和快速Herbst 机动中的摇滚运动，可以发现，拉起速度和圆锥运动速度的不同导致摇滚运动存在明显差异。慢速Herbst 机动完成时间长，摇滚运动类型多且复杂，摇滚周期数较多，运动振幅较大；快速Herbst 机动完成时间短，摇滚运动类型为单一的类正弦摇滚形式，摇滚完成的周期数较少，运动振幅较小。

3.3 Herbst 机动中摇滚运动产生的主要阶段

对比慢速和快速Herbst 机动各阶段的摇滚运动发现，摇滚运动主要出现在拉起阶段和下俯阶段，而在圆锥运动阶段模型运动表现为微振，没有出现明显的摇滚运动。但是，此时不能得到圆锥运动阶段对摇滚运动没有影响的结论，因为Herbst 机动到θ= 70°时，对应模型在固定俯仰角θ= 70°的运动是微振，如图11 所示。原本不摇滚的状态不适合用来解释圆锥运动对机翼摇滚是否存在影响的问题。

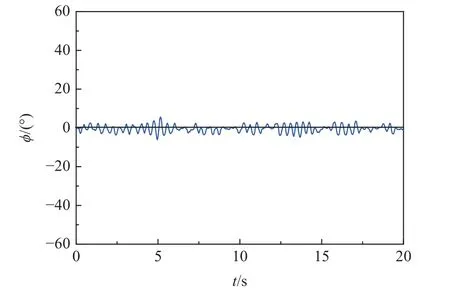
图11 固定俯仰角θ =70°的摇滚运动Fig.11 Roll oscillations at fixed pitch angle of θ =70°

为了确定Herbst 机动中产生摇滚运动的主要阶段，需要明确圆锥运动对摇滚运动的影响。为了使圆锥运动阶段，模型仍出现摇滚运动，假设了Herbst50 机动试验工况，研究圆锥角和圆锥运动速度等圆锥运动参数对Herbst 机动中摇滚运动的影响规律。注意的是，Herbst50 的圆锥角为50°不是真实的Herbst 机动，但它包括俯仰角变化（拉起或下俯）和绕速度矢量的圆锥运动角变化，可认为是类Herbst 机动。

1）圆锥角 ΛCA的影响

图12 为 ΛCA= 50°时慢速和快速Herbst50 机动中的摇滚运动。与图7 和图9 所示的Herbst70 摇滚运动对比，在俯仰角拉起和下俯中，Herbst50 的摇滚运动可看成截取Herbst70 到俯仰角θ=50°的摇滚运动，Herbst50 的圆锥运动阶段出现了明显的摇滚运动。

图12 Herbst50 机动中的摇滚运动Fig.12 Roll oscillations in Herbst50 maneuver

在慢速机动中，Herbst70 工况是绕零滚转角的微振，Herbst50 工况是绕零滚转角的大振幅摇滚运动，如图12 (a)所示。这是因为圆锥角数值上等于拉起结束俯仰角，决定了拉起结束时的运动形态，而该运动形态恰是进入圆锥运动时的初始状态，即改变圆锥角本质上是通过改变拉起结束俯仰角，进而影响了圆锥运动中的摇滚运动。

在快速机动中，圆锥角带来的影响更加明显，对于图9 中Herbst70 工况，圆锥运动中的摇滚运动为微振，而Herbst50 工况，模型却呈现大振幅的摇滚运动，如图12(b)所示。这仍是因为进入圆锥运动的拉起结束俯仰角不同导致的。Herbst50 工况，快速拉起到50°俯仰角结束时，模型摇滚运动表现为大振幅摇滚形式，圆锥运动中仍然是大振幅摇滚运动形式。

2）圆锥运动速度 ωc的影响

通过单独圆锥运动研究圆锥运动速度 ωc对摇滚运动的影响。ΛCA= 50°，圆锥运动速度0(°)/s、20 (°)/s、100 (°)/s 和360 (°)/s。当 圆 锥 运 动 速 度 为360 (°)/s 时，加速和减速段是圆锥运动角360°，运动范围为圆锥运动角0°～3 960°（11 圈）；当拉起速度为其他时，加速和减速段是圆锥运动角20°，运动范围为圆锥运动角0°～360°。电磁闸在匀速圆锥运动后释放滚转自由度。

图13 为不同圆锥运动速度下模型在圆锥运动中的摇滚运动。为了便于对比，图中截取了释放滚转自由度5 s 的运动数据。图13(a)为圆锥运动速度为零的摇滚运动形态，即没有圆锥运动而模型在固定俯仰角50°的机翼摇滚运动。图14 为圆锥运动速度对摇滚运动特性的影响，图中误差中心点表示摇滚运动的平衡位置，误差带宽度表示运动振幅。可以看出：①摇滚运动要经历建立过程才能到达稳态摇滚，稳态摇滚时振幅基本不再变化；②不同圆锥运动速度下稳态摇滚运动形态均表现为极限环摇滚运动，与固定俯仰角50°的稳态摇滚相同。③不同圆锥运动速度下摇滚运动的运动振幅、平衡位置和主频基本不变，说明圆锥运动本身对机翼摇滚基本没有影响。

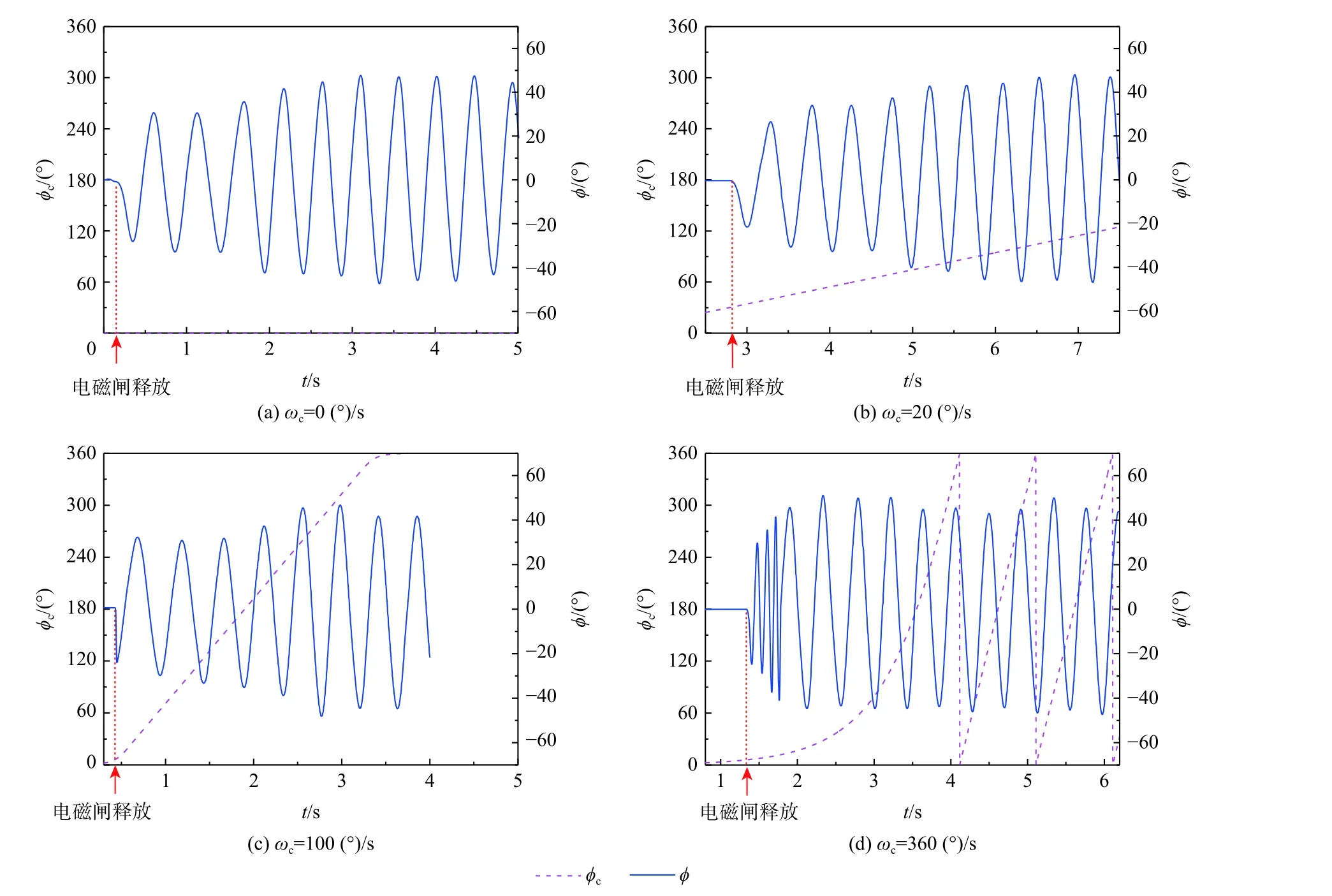
图13 单独圆锥运动中的摇滚运动Fig.13 Roll oscillations in single coning motion

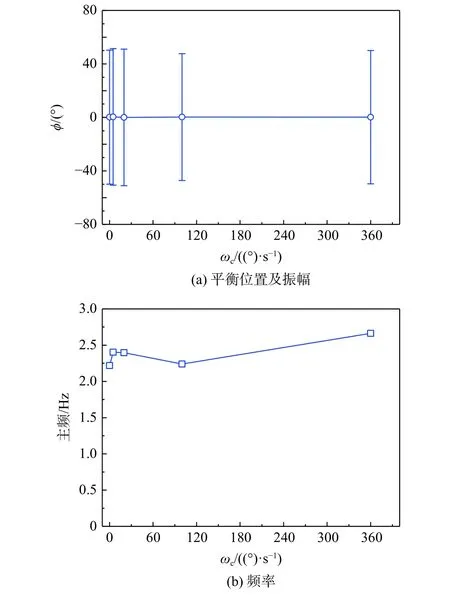
图14 圆锥运动速度对摇滚运动的影响Fig.14 Effect of coning rate on roll oscillations

在圆锥运动中，圆锥运动速度是绕速度矢量的旋转速度，模型体轴的不同截面产生附加线速度，等价于附加了侧滑。不考虑机翼滚转，只考虑模型机身情况下，机身不同轴向截面附加侧滑角 βadd的计算公式为

式中：Lc为机身不同轴向截面中心点距圆锥运动轴与机体轴交点即运动中心的距离，圆锥运动轴与机体轴交点距离机头顶点375 mm；V∞为自由来流速度。图15 为圆锥运动中机身附加侧滑角沿体轴截面的变化规律。在机头和机尾附近的附加侧滑角较大。当 ωc≤ 100 (°)/s 时，最大附加侧滑角小于1°，只有当 ωc= 360 (°)/s 时，最大附加侧滑角约为3.6°。考虑到模型摇滚时，俯仰角（支杆支撑角）和滚转角可转化为有效迎角和有效侧滑角 βeff。反之亦然。图16 为θ= 50°时模型有效侧滑角 βeff随滚转角的变化规律。最大附加侧滑角3.6°，相当于此时模型具有小于2°的初始滚转角。摇滚运动研究表明[24-25]，初始滚转角对摇滚运动形态基本没有影响。因此，尽管存在附加侧滑角，也能够理解圆锥运动对摇滚运动几乎没有影响。此外，圆锥运动中摇滚运动受拉起结束时摇滚运动的主导，圆锥运动中的摇滚运动是从属于拉起阶段的。

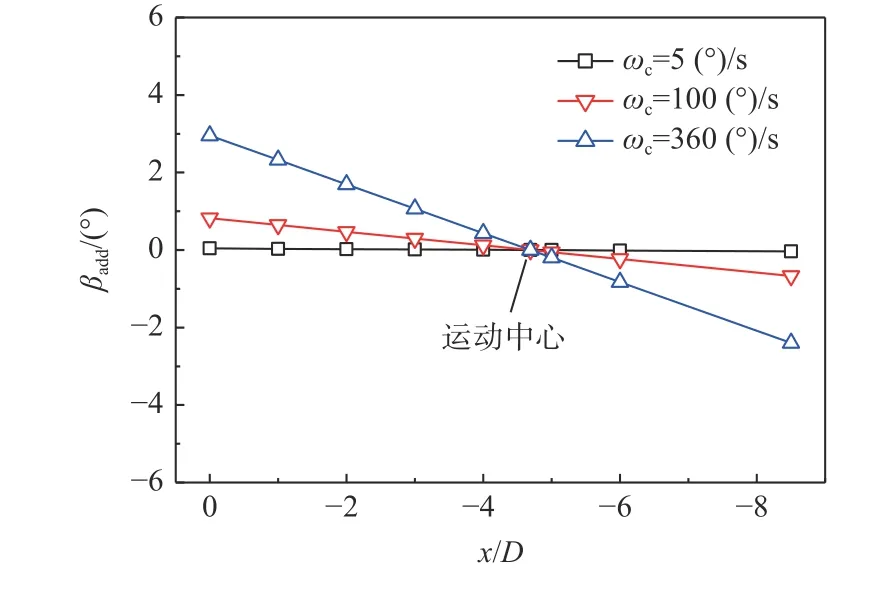
图15 圆锥运动中附加侧滑角βadd 随轴向位置的变化Fig.15 Variation of βadd with axial position in coning motion

图16 有效侧滑角βeff 随滚转角的变化规律（θ=50°）Fig.16 Variation of effective sideslip angle βeff with roll angle while θ is 50°

综上可知，Herbst 机动中摇滚运动的主要来源阶段是俯仰拉起阶段。下俯作为拉起的逆向过程，摇滚运动是逐步消失的。考虑研究产生摇滚运动的流动机理对于提出流动控制技术方案更有意义。因此，研究Herbst 机动中的摇滚运动应将研究重点放在俯仰角拉起过程。

4 俯仰角拉起过程中的摇滚运动

4.1 零拉起速度下的摇滚运动

零拉起速度时，模型在不同固定俯仰角下的运动形态如图17 所示，其中NWR 为摇滚运动，FP 为微振，LCO 为单极限环，CO 为混沌摇滚。图中误差中心点表示该俯仰角下摇滚运动的平衡位置，误差带宽度表示运动振幅。图18 为不同俯仰角下典型摇滚运动的时间历程曲线。图19 和图20 分别为典型摇滚运动的相图和频谱分布。

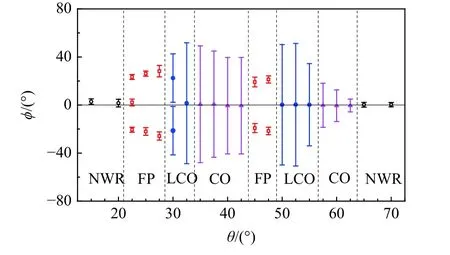
图17 不同固定俯仰角下的摇滚运动形态Fig.17 Pattern of rolling oscillation at various fixed pitch angles

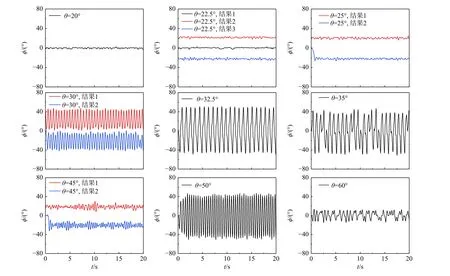
图18 固定俯仰角下摇滚运动时间历程Fig.18 Time histories of roll oscillations at fixed pitch angles

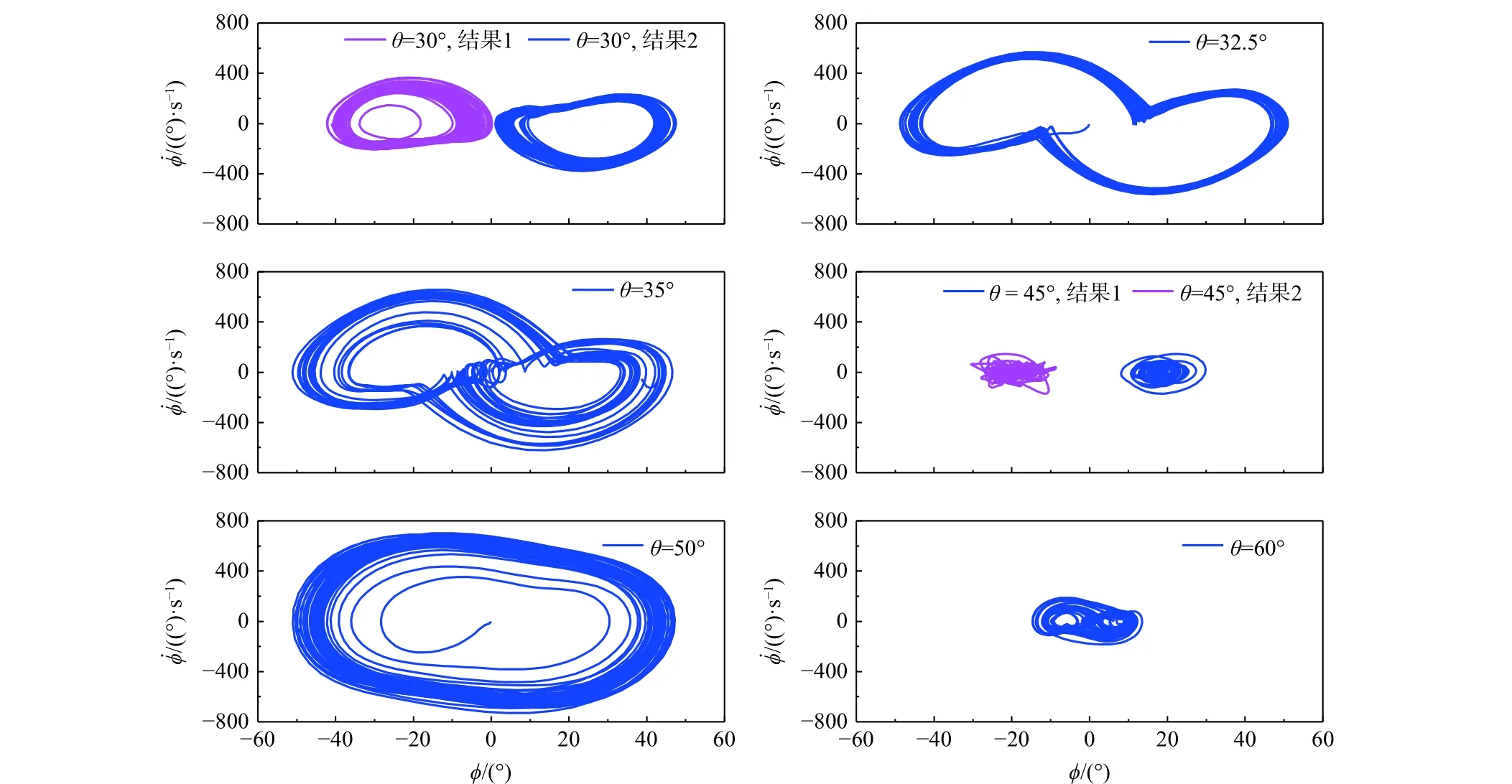
图19 固定俯仰角下摇滚运动的相图Fig.19 Phase plots of roll oscillations at fixed pitch angles

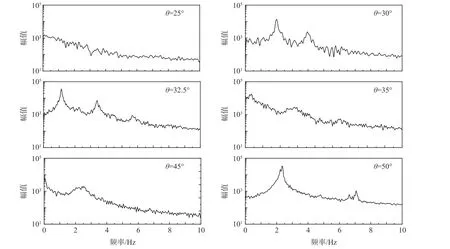
图20 固定俯仰角下摇滚运动的频谱Fig.20 Spectra of roll oscillations at fixed pitch angles

当θ≤ 20°时，没有产生摇滚运动；当θ=22.5°～27.5°时模型出现横向偏离，θ= 22.5°为过渡状态，即可平衡在零滚转角附近，也可出现横向偏离，平衡在非零滚转角约±21°附近，θ> 22.5°，不能平衡在零滚转角附近，只能出现横向偏离，并平衡在非零滚转角附近，运动形态为绕多个稳定点的微振；当θ= 30°～32.5°时，θ= 30°，模型出现绕正或负滚转角的摇滚运动，与运动对应的相图轨迹收敛到单个轨道上，摇滚运动出现明显的主频，约2 Hz，运动形态为单极限环。θ= 32.5°，模型出现绕零滚转角的单极限环摇滚，摇滚相图收敛到单个轨道上，摇滚主频约1 Hz，运动形态为单极限环；当θ=35°～42.5°时，模型出现绕零滚转角的不规则摇滚运动，相图轨迹包含了2 个相连的轨道，连接位置不是确定的，即运动从一个轨道跳跃另一个轨道是随机的，运动不可预测，也不具有重复性，相应的摇滚运动频谱呈现宽频分布，没有主频，符合混沌摇滚运动的特征，运动形态为混沌摇滚；当θ=45°～47.5°时，模型出现横向偏离。相图中轨迹收敛到点，运动形态为绕多个稳定点的微振；当θ=50°～55°时，模型出现绕零滚转角的摇滚运动，相图中轨迹收敛到单个轨道上，摇滚运动主频约2.5 Hz，运动形态为单极限环；当θ= 55°～60°时，模型出现绕零滚转角的不规则摇滚运动，相图中轨迹由相连的2 个轨道构成，与θ= 35°～42.5°的运动形态类似，没有主频，运动形态为混沌摇滚；当θ≥ 65°时，没有产生摇滚运动。

从运动形态可以看出，俯仰角是摇滚运动的关键参数。当0° <θ≤ 20° 和65°≤θ≤ 70°时，模型平衡在零滚转角，为不摇滚区；当22.5°≤θ≤ 60°时，模型摇滚运动形态复杂，为摇滚区。在摇滚区存在3 种摇滚运动类型：绕多个平衡位置微振、单极限环和混沌摇滚。

4.2 拉起速度对摇滚运动的影响

拉起运动的俯仰角范围0°～70°，匀速拉起速度 ωp= 0.5～75(°)/s，为了保证与Herbst 机动中拉起过程一致，电磁闸释放俯仰角同样设置在20°。拉起中的摇滚运动随拉起速度可以分为以下3 个分区：准静态区（低拉起速度）、过渡区（中拉起速度）和类正弦运动区（高拉起速度）。

1）准静态区（0 (°)/s <ωp≤ 1 (°)/s）

当模型以拉起速度0 (°)/s <ωp≤ 1 (°)/s 匀速拉起时，由于拉起速度较低，拉起摇滚运动主要特征是当拉起运动经过某俯仰角时出现对应固定俯仰角下的运动形态，摇滚运动曲线如同“沿着”固定俯仰角运动图谱发展，称为准静态区。图21 为ωp= 0.5 (°)/s和ωp= 1 (°)/s 时拉起中的摇滚运动与固定俯仰角下运动图谱。摇滚运动曲线基本上“包裹”着固定俯仰角下的运动图谱。摇滚运动曲线“跟随”着固定俯仰角的运动图谱进行演化，如模型到达20°俯仰角时出现横向偏离，到达30°俯仰角时出现单侧极限环摇滚，到达45°俯仰角时出现横向偏离，50°俯仰角时出现大振幅极限环摇滚运动等等。图22为ωp= 0.5 (°)/s 拉起时运动俯仰角段和固定俯仰角的运动。可知拉起俯仰角段与该固定俯仰角下的摇滚运动基本一致。

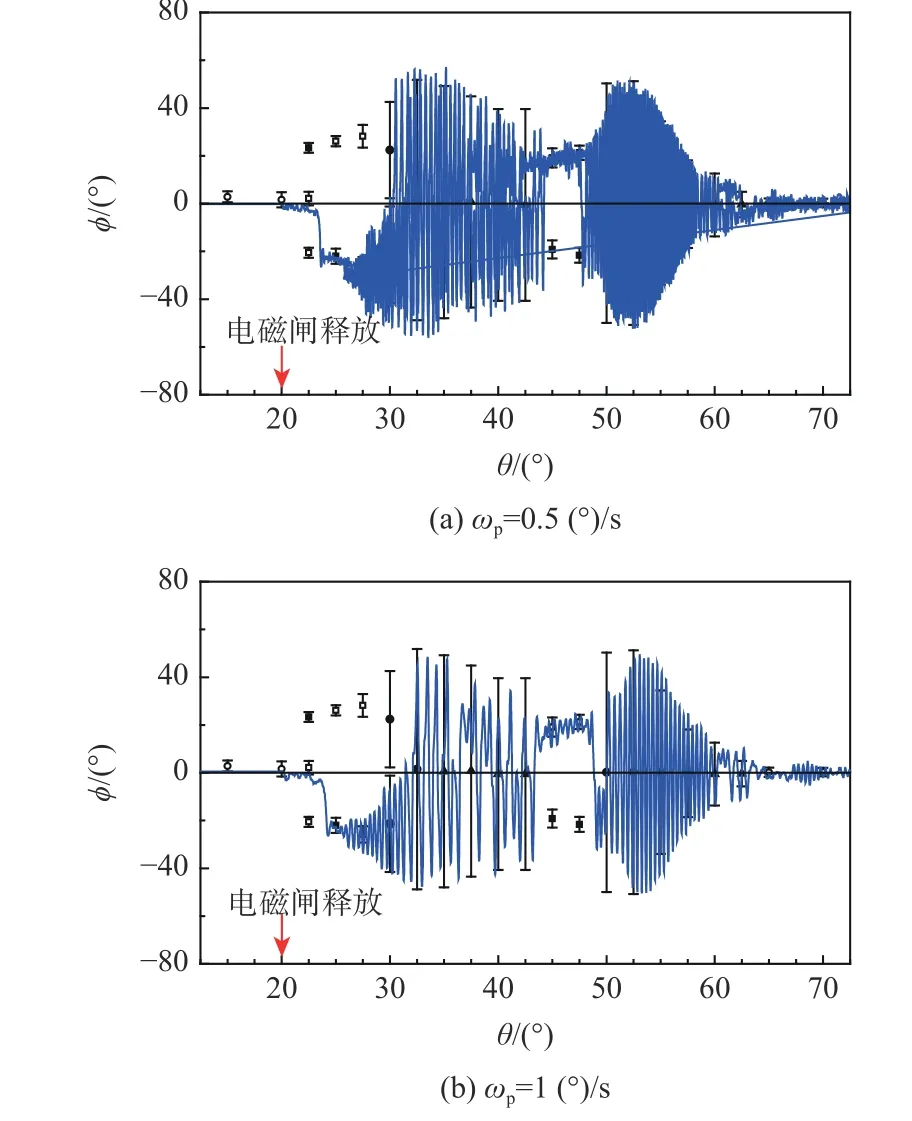
图21 准静态区拉起中的摇滚运动Fig.21 Roll oscillations in pitch up at quasi-static region

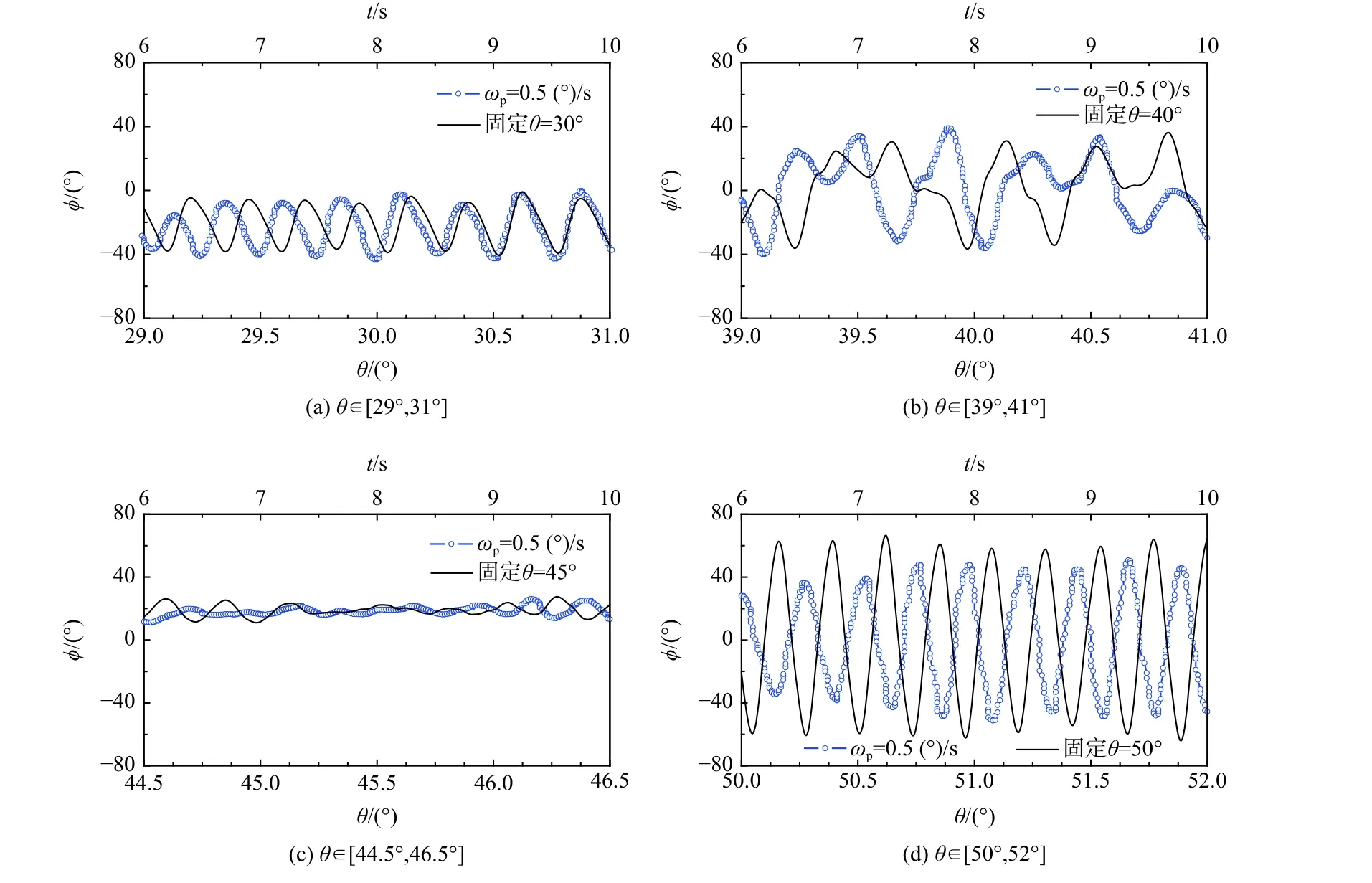
图22 拉起俯仰角段和固定俯仰角的运动对比Fig.22 Comparison of roll oscillations between undergoing pitch-up angles and corresponding fixed pitch angles

2）过渡区（2 (°)/s≤ωp≤15 (°)/s）

图23 为过渡区不同拉起速度下拉起摇滚运动与固定俯仰角图谱。当模型以2～15 (°)/s 匀速拉起时，摇滚运动出现迟滞现象，随拉起速度增加运动迟滞现象越来越明显。在过渡区ωp= 2 (°)/s 时，拉起摇滚虽然仍能“沿着”固定俯仰角运动图谱，但是在对应固定俯仰角的运动周期个数减少，振幅下降。随着拉起速度ωp的增加，运动迟滞现象主要表现在3 个方面：①摇滚运动首次横向偏离到最大滚转角对应的俯仰角变大，拉起摇滚运动的周期数减少；②摇滚运动将省略掉部分固定俯仰角的运动类型；③当拉起速度ωp= 15 (°)/s 时，摇滚运动中没有 出 现 固 定 俯 仰 角 段22.5°～27.5°和45°～47.5°的稳定点微振运动。

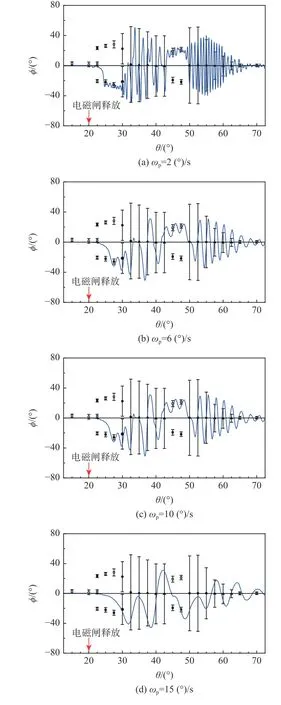
图23 过渡区拉起中的摇滚运动Fig.23 Roll oscillations in pitch up at transition region

图24 为过渡区摇滚运动周期数和运动频率随拉起速度的变化规律。运动周期以模型首次偏到最大滚转角（波谷）为起点，到达最近波谷为1 个周期，范围从摇滚运动首次达到最大滚转角的俯仰角到结束俯仰角，同时计算出拉起摇滚运动频率。当ωp= 2～8 (°)/s 时，运动周期数呈快速减小趋势，而拉起摇滚频率基本保持在0.5 Hz；当ωp= 10～15 (°)/s时，运动周期数呈平缓减小趋势，拉起摇滚频率基本保持在0.45 Hz 左右。频率曲线表现出2 个平台，可能是稳定点微振形式的摇滚运动逐步消失导致的。

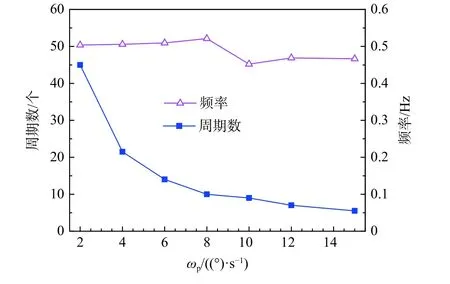
图24 过渡区拉起中摇滚运动的周期数和运动频率Fig.24 Number of periods and frequencies of roll oscillations undergoing pitch up at transition region

3）类正弦区（20 (°)/s ≤ωp≤70 (°)/s）

当模型以20～70 (°)/s 匀速拉起时，摇滚运动基本不体现固定俯仰角的运动图谱，表现为减幅类正弦摇滚运动。这与旋成体机身的组合体[21]类似。图25 为类正弦摇滚运动随拉起速度的变化规律。图26 为模型首次偏离的最大滚转角 ϕini和最大滚转角对应的俯仰角 θini随拉起速度的变化规律。随拉起速度的增加，运动迟滞越明显，模型首次偏离的最大滚转角 ϕini呈先增大后减小的趋势，而首次偏离最大滚转角对应的俯仰角 θini逐渐变大。

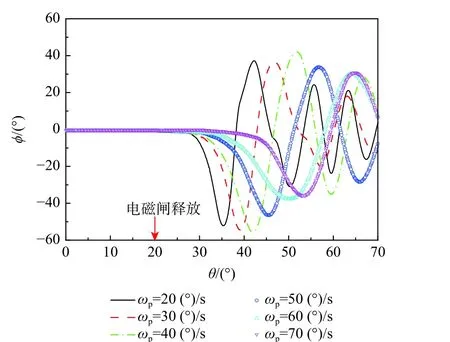
图25 类正弦区拉起中的摇滚运动Fig.25 Roll oscillations undergoing pitch up at sine-like region

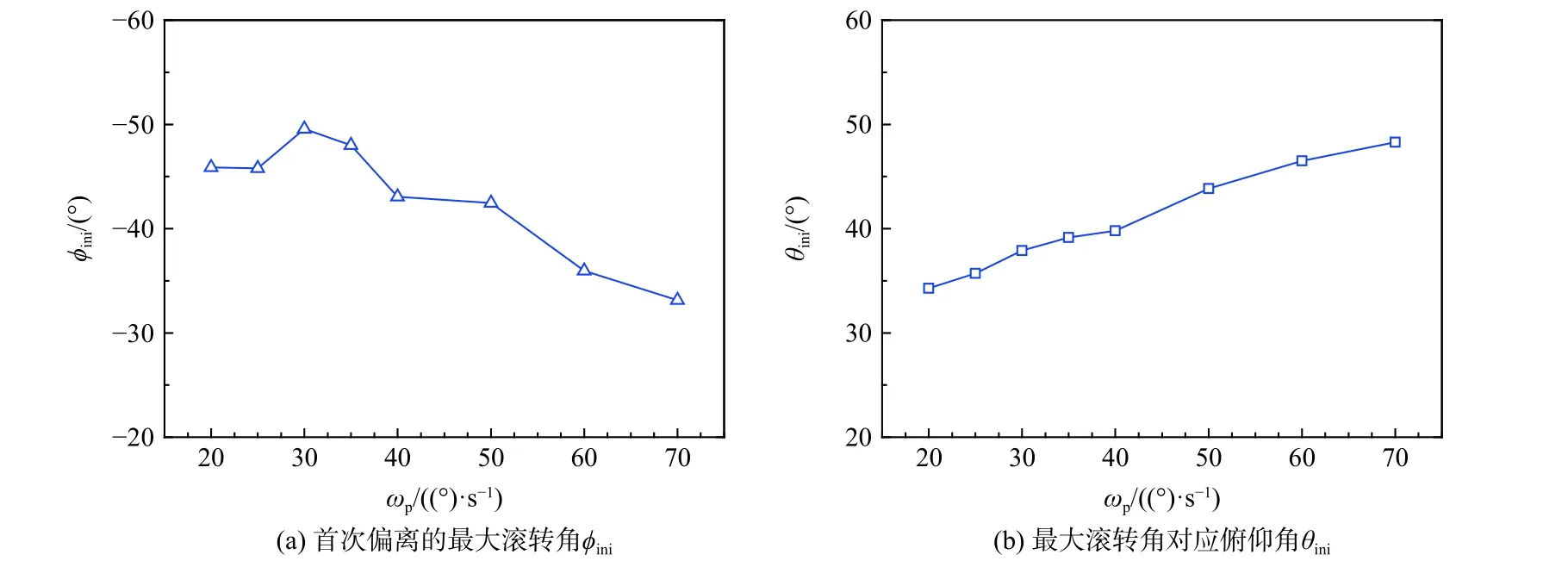
图26 类正弦区首次偏离的最大滚转角和对应俯仰角Fig.26 The maximum firstly-deflected roll angle and related pitch angle at sine-like region

快速拉起中的类正弦摇滚与快速Herbst 机动中摇滚运动吻合，侧面说明了Herbst 机动中产生摇滚运动的主要过程是俯仰角快速拉起过程。

4.3 雷诺数对快速拉起摇滚运动的影响

图27 为雷诺数ReD对ωp= 30 (°)/s 时拉起中摇滚运动的影响。当ReD从0.53×105增加到1.33×105时，模型首次偏离的最大滚转角ϕini逐渐增加，对应的俯仰角θini前移。当ReD从1.33×105增加到1.87×105时，模型首次横向偏离最大滚转角 ϕini逐渐减小，对应的俯仰角 θini继续前移。当雷诺数小于1.33×105时，模型摇滚能持续1 个周期左右的运动；而当雷诺数大于1.33×105时，模型摇滚能持续2 个周期左右的运动。由于拉起速度一定，拉起经历的时间相同，这段时间内持续周期数的增加意味着拉起摇滚运动频率的提高。因此，雷诺数不改变拉起摇滚的类正弦运动形式，增加雷诺数可提高拉起摇滚运动的频率。

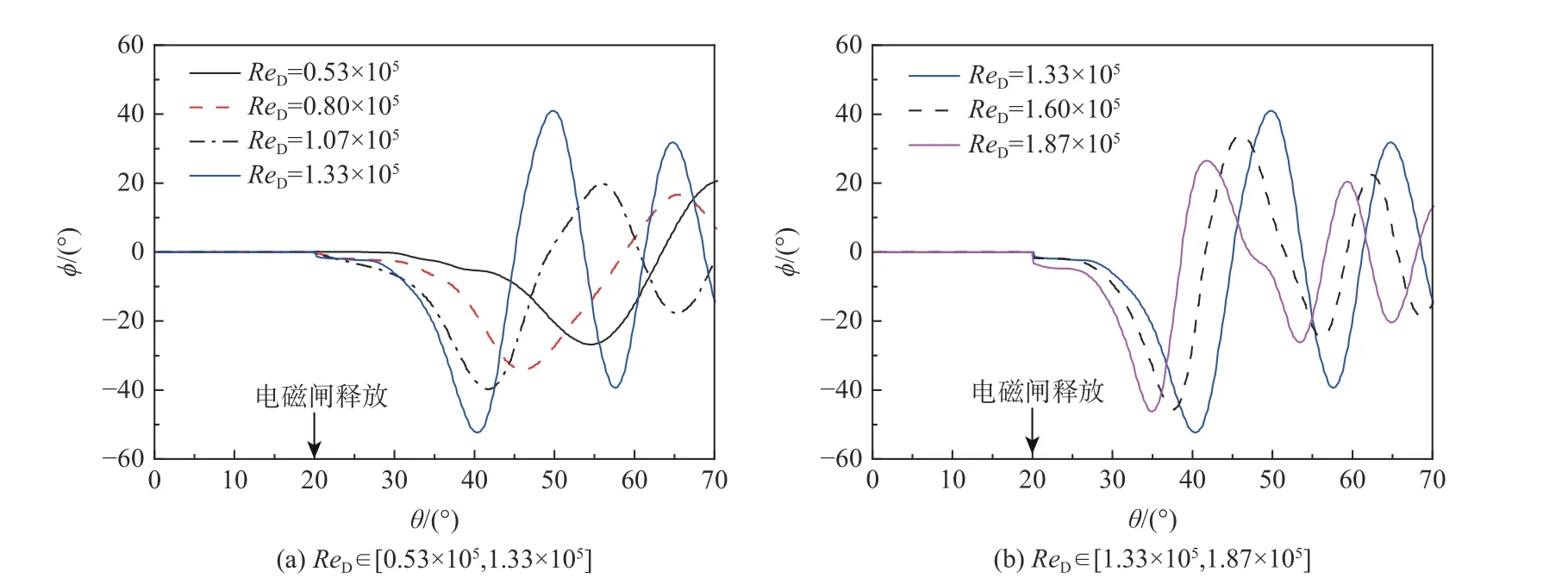
图27 ReD 对快速拉起摇滚运动的影响（ωp = 30 (°)/s）Fig.27 Effect of ReD on wing rock undergoing fast pitch-up （ωp = 30 (°)/s）

4.4 拉起减缩频率对快速摇滚运动的影响

快速拉起减缩频率（reduced pitch rate）是斯特劳哈尔数在拉起运动过程中的反映，无量纲快速拉起减缩频率 ω∗p的计算公式为

式中：L为机身长度。若雷诺数一定，快速拉起减缩频率 ω∗p对拉起摇滚运动的影响等同于拉起速度，在拉起速度的影响已经讨论过，不再讨论。

此处考虑同时改变拉起速度和来流速度使快速拉起减缩频率保持不变，研究该情况下的模型拉起摇滚运动形态。图28 为 ω∗p= 0.01 时快速拉起中的摇滚运动。可以看出，在试验的ReD数范围内，当拉起减缩频率一定时，拉起摇滚曲线在拉起到俯仰角50°之前基本重合，而在俯仰角50°之后运动曲线比较分散。因此，拉起减缩频率在一定俯仰角范围内，可以作为研究真实飞机和风洞试验模型快速拉起摇滚运动的无量纲参数。

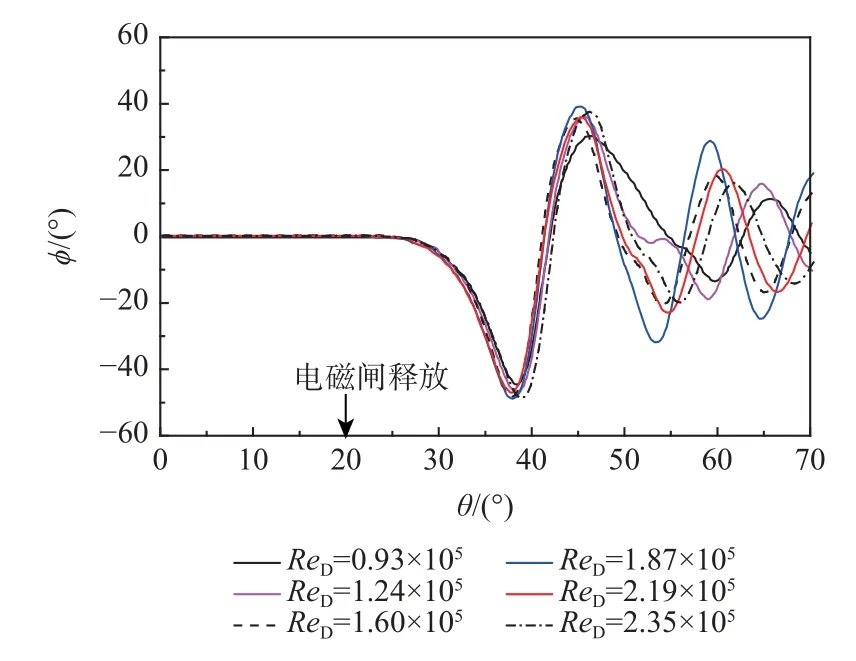
图28 减缩频率 ω∗p =0.01 时的快速拉起摇滚运动Fig.28 Wing rock in fast pitch-up at reduced pitch rate of 0.01

5 结 论

1）尖侧缘机身布局在Herbst 机动中出现了明显的摇滚运动形态，摇滚运动产生的主要阶段是俯仰角拉起阶段，而Herbst 机动中的圆锥运动对摇滚运动基本没有影响。

2）在俯仰拉起阶段，摇滚运动随拉起速度可分为准静态区（0 (°)/s < ωp≤ 1 (°)/s），过渡区（2 (°)/s ≤ωp≤15 (°)/s）和类正弦区（20 (°)/s ≤ ωp≤70 (°)/s）。在准静态区，拉起运动经过某俯仰角时出现该固定俯仰角下的运动形态。在过渡区，出现了迟滞现象，拉起运动的摇滚运动虽然仍是固定俯仰角下的运动图谱的体现，但是在对应固定俯仰角的运动周期个数减少，振幅下降。在类正弦区，摇滚运动表现为减幅类正弦摇滚运动。

3）雷诺数不改变快速拉起中的摇滚运动形式，增加雷诺数可提高拉起中的摇滚运动频率。

4）在快速拉起摇滚运动的类正弦区，当拉起减缩频率为0.01 时，拉起摇滚运动曲线在俯仰角50°之前基本重合，在俯仰角50°之后较为分散，在一定的俯仰角范围内，拉起减缩频率可作为尖侧缘机身布局拉起中的摇滚运动无量纲参数。

后续可开展尖侧缘机身布局在Herbst 中摇滚运动的流动机理的研究，尤其是应继续针对俯仰角快速拉起中摇滚运动的流动机理开展研究。