飞机轮组滑水行为与道面积水附加阻力
李岳,宗辉杭,蔡靖,戴轩
(中国民航大学 交通科学与工程学院,天津 300300)
根据国际航空运输协会统计,近十年全球共发生708 起重大航空安全事故,飞机冲偏出跑道事故占比达23%,在全部事故类别中排名第一[1],有半数此类事故伴随道面积水情况。飞机地面高速滑行时道面积水可引起轮胎附着力与附加阻力降低,诱发单个轮胎滑水乃至整机滑行姿态失控。因此,飞机轮组滑水行为与附加阻力是滑水问题研究的重点。
美国国家航空航天局(NASA)较早开展了飞机轮胎滑水性能试验,在此基础上建立临界滑水速度(后文简称vP)计算公式[2](NASA 公式)。一般认为轮胎接触面上动水压力的竖向抬升作用是导致滑水的主要原因,后续研究中广泛采用道面对轮胎竖向支撑力作为轮胎滑水判定指标[3-8]。近年来,有限元软件和流固耦合算法的成熟使得仿真分析逐步成为滑水研究的常见手段。Ong 和Fwa[3-4]通过轮胎与积水路面流固耦合分析,验证当流体对轮胎竖向支撑力与车轮荷载平衡时即发生打滑现象。Fwa 和Ong[5]研究了胎面下部流体抬升力对轮胎接触面法向接触力的削弱效应。Tang 等[6]基于实际路面扫描数据建立仿真分析模型,探讨单个轮胎在不同降雨强度和路面渗透性下的滑水现象。Srirangam 等[7]采用单轮仿真分析模型计算不同滑移率下的vP,分析路面积水引起的制动牵引力和转向力损失。刘修宇等[8]开展轮胎滑水行为仿真,分析滑水前后轮胎路面竖向接触力变化。黄晓明等[9]通过ABAQUS 仿真回归得出了水流竖向托举力与水膜厚度和行驶速度的关系式。郑彬双等[10]建立单轮滑水分析模型,研究湿滑状态下沥青路面附着系数,探讨滑移率对轮胎滑水的影响。闫珅[11]提出了道面污染物阻力的计算公式并对污染跑道条件下的飞机起降性能进行分析。李岳等[12]开展轮胎与积水道面流固耦合分析,推导了轮胎接触面动水压强与道面竖向支撑力表达式。Fwa 等[13]通过有限元仿真探讨临界滑水速度与路面车辙深度之间的关系。
综合来看,以往研究工作主要关注单轮滑水形成过程,将道面支撑力下降至0 时刻作为滑水临界状态,假定滑水过后轮胎与道面摩擦力完全消散,而对轮胎所受道面积水附加阻力讨论比较少见。由于道面支撑力与飞机行进方向正交,而积水附加阻力与飞机行进方向一致或处于同一运动平面内,滑水临界时刻积水附加阻力曲线出现反弯点,符合滑水状态判定需要,因而积水附加阻力更适合作为滑水分析指标。当考虑沥青道面不均匀积水条件时,轮组内部存在滑水过程差异,无法用单轮滑水行为表征。
本文以积水附加阻力为切入点,研究单个飞机轮胎与轮组滑水行为,分析积水附加阻力形成原理,建立流固耦合仿真模型,探讨不同滑行状态与积水条件下附加阻力规律,讨论轮组附加阻力特征与叠加条件,为轮胎滑水条件判定和滑行姿态控制提供分析依据。
1 积水附加阻力构成
道面积水主要通过挤压和喷流2 种方式对地面高速滑行滚动轮胎产生阻力效应,削弱轮胎与道面接触条件,降低飞机起降性能,增大滑水事故发生几率。英国布里斯托尔大学通过室内试验研究了飞机轮胎溅水行为[14],轮胎溅水喷流如图1所示。
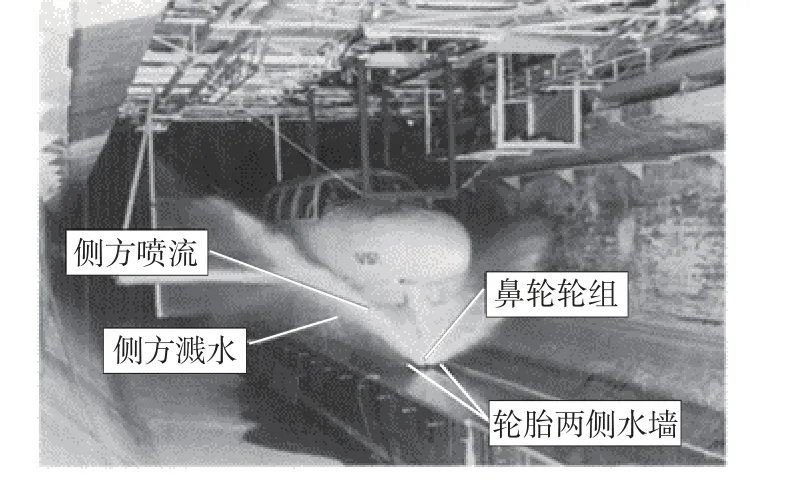
图1 飞机轮胎溅水喷流试验Fig.1 Water spread test of aircraft tire
轮胎驶过积水道面时积水与轮胎前缘接触,因挤压效应形成位移阻力分量Ddisp;部分流体向下通过底部胎纹构成的排水通道向后排出,轮胎接触面上摩擦阻力分量Dfric随速度增加而逐步减弱;部分流体在挤压作用下横向绕流,与轮胎边缘阻挡水墙冲撞形成侧方喷流;其中指向两侧的低强度喷流水柱较弱,对飞机影响有限;指向侧后的高速喷流击中机身或起落架时会产生冲击阻力分量Dimpa;喷溅到机体上的水沿着表面流动继而形成表面阻力分量Dsurf,即有道面积水总附加阻力为
Dimpa和Dsurf由溅水喷流引起,与机身外形及投影面积相关。文献[15]的研究表明,前起落架是Dimpa和Dsurf的主要来源,主起落架溅水喷流方向相对远离机身,当积水厚度小于6.5 mm 时溅水喷流阻力效应微弱[15]。轮胎发生滑水后,Dfric近似消散,因而可以将Ddisp作为轮胎附加阻力代表值,该指标是本文滑水分析的重点。主起落架轮胎位移阻力为[16]
式中:ρ为积水密度;vG为 地面滑行速度;n为轮组系数,典型双轮起落架可近似取2.0,即为单轮式的2 倍。阻力系数CD可通过有限元仿真计算得出,轮胎发生滑水前近似取保守值0.75,当vG>vP时需考虑轮胎滑水影响。轮胎前缘积水接触面面积S为[16]
式中:d为积水厚度;b为接触面有效宽度;W为轮胎宽度;δ为轮胎垂直形变,可由轮胎“载荷-变形”曲线查得。轮胎发生滑水时,表层水膜将轮胎与道面完全分隔,图1 中溅水喷流路径随之改变,滑水速度影响因子F为
由式(2)可知道面积水附加阻力随滑行速度增加而增大,在vG/vP<1 阶段,F保持为1.0,无修正作用,此时附加阻力仅为关于vG的二次递增函数,vG/vP=1.0时达到最大值;滑水速度对附加阻力影响主要体现在vG/vP>1.0阶 段,F随滑行速度增加而出现非线性衰减;图2 中滑水临界状态前后附加阻力变化规律有明显转折,可作为滑水判定依据,用于飞机滑水分析。

图2 滑水速度影响因子变化曲线Fig.2 Variation curve of impact factor of taxing speed
2 飞机轮组滑水分析模型
选取空客A320 飞机为案例,采用ABAQUS 软件建立主起落架双轮流固耦合滑水分析模型。结合文献[12]中的研究经验,选取水流冲击方式模拟轮组与积水道面相互作用,计算效率及精度可满足分析需要[17]。
2.1 模型参数
基于实测数据绘制主起落架轮胎横断面,规格为46×17R20,绕轮轴旋转一周生成三维实体模型,断面细部尺寸如图3 所示。
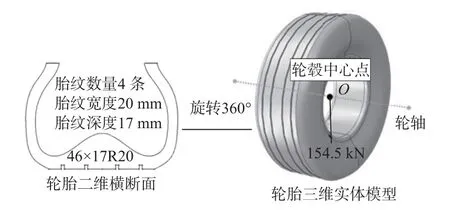
图3 机轮模型生成过程Fig.3 Generation process of aircraft tire model
轮胎模型关于轮毂中心O点刚性耦合,并在该点施加轮载154.5 kN,通过调整轮载标准值考虑高速着陆条件下升力对飞机轮胎滑水的影响;轮壁内侧施加1 140 kPa 均匀分布的压力,模拟轮胎充气效果;查询飞机设计手册双轮中心间距0.93 m。轮胎结构等效为具有统一超弹性特性的均质橡胶材料,采用Mooney-Rivlin 本构模型模拟[18],相关参数如表1 所示[19]。
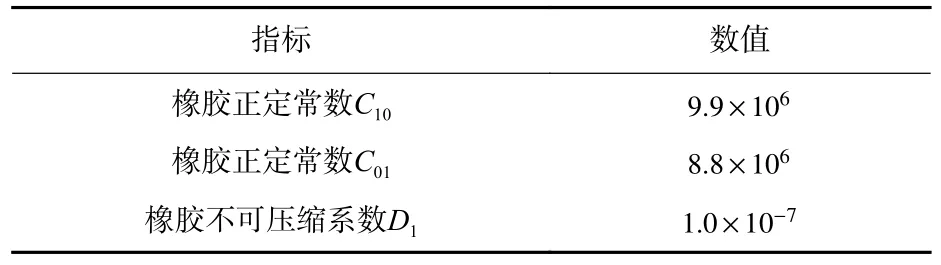
表1 轮胎材料物理力学参数[19]Table 1 Mechanical parameters of tire material[19]
跑道接地带长期承受机轮反复碾压作用,容易发生轮辙变形(见图4(a)),形成局部积水增厚和不均匀分布,对轮组阻力影响不容忽视。对此,参照美国国家道面测试中心试验建立带轮辙道面分析模型,对照平整道面情况。该试验对沥青道面进行飞机轮组足尺循环加载,模拟加载位置横向偏移,轮辙断面更符合实际道面变形特征[20]。
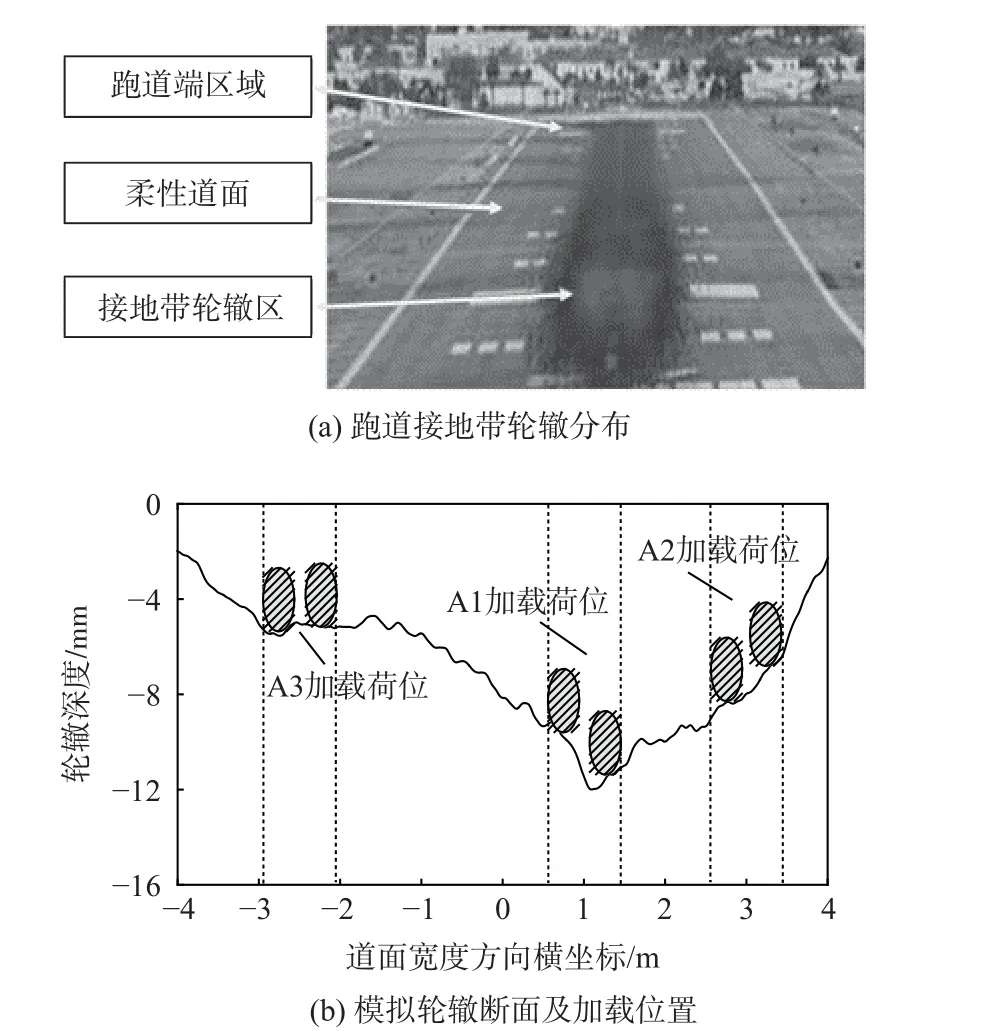
图4 道面模型断面特征Fig.4 Cross-sectional feature of pavement model
图4(b)中轮辙断面总影响宽度超过9.0 m,而飞机轮组宽度仅为136 cm,轮辙影响宽度达到飞机轮组宽度的6 倍以上,最大轮辙深度为12.1 mm,对此定义3 组加载荷位开展对比分析。其中,A1 加载荷位对应轮辙横断面最大深度处,轮组整体积水深度较大;A2 加载荷位对应轮辙横断面斜率较大处,左右轮胎之间积水深度差较大;A3 加载荷位对应轮辙横断面平坦段,轮组内部积水深度差较小,但整体积水厚度仍高于平整道面情况。3 组荷位涵盖了跑道接地带典型积水特征区域,可用于开展轮组滑水仿真分析(注:图中椭圆形仅为轮组加载荷位示意,非成比例绘制)。
装配完成后的轮组滑水仿真模型如图5 所示,道面平面尺寸经反复试算确定为2.0 m×1.5 m,对图4 中不同轮辙特征区分段进行模拟;根据跑道允许起降条件确定积水层厚度范围为3~13 mm[12],且在积水层上部定义300 mm 的厚空气层,为溅水喷流提供充分的运动表达空间。积水层物理参数在文献[21]中已详细说明,此处不再赘述。
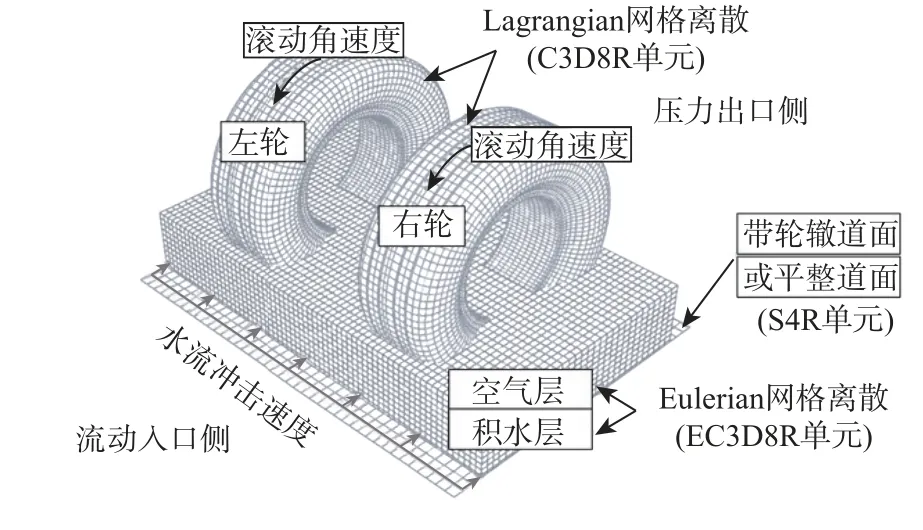
图5 飞机轮组滑水仿真模型Fig.5 Simulation model of hydroplaning analysis of aircraft landing gears
采取耦合的欧拉拉格朗日(coupled Eulerian-Lagrangian,CEL)算法求解流固耦合问题,飞机轮组由8 节点线性六面体减缩积分单元(C3D8R)离散,道面采用刚性壳单元模拟,滑水过程中道面无变形发展;积水和空气层采用欧拉网格离散(EC3D8R 单元)。仿真开始后水流由入口侧按一定速度冲击转动轮胎形成附加阻力,在轮胎周围产生溅水喷流,随后由压力出口侧排出;调节水流速度使轮胎逐步达到临界滑水状态。受道面轮辙影响,各个轮胎运动协调关系相互独立,保证其与道面充分接触;轮胎中心转动角速度与水流速度匹配,滑移率保持为1.0。
2.2 模型验证
轮胎刚度特征多采用竖向位移量或轮印面积指标进行验证,在文献[19,21-24]中被广泛采用,而轮胎滑水行为特征是模型验证的难点。在ABAQUS分析中定义2 组历程输出,分别提取轮胎迎水面上位移阻力Ddisp和道面对轮胎竖向支撑力的结果,如图6 所示。
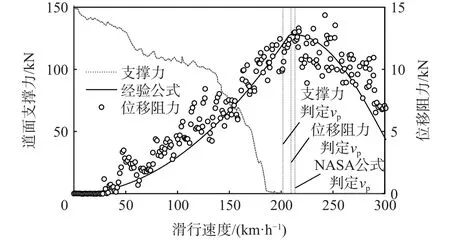
图6 轮胎模型滑水特性验证Fig.6 Verification of hydroplaning feature of tire model
图6 中支撑力曲线随滑行速度增加逐步下降,支撑力降至0 时速度约为202 km/h,与NASA 公式计算该胎压下vP=214 km/h 较为接近。位移阻力以散点形式绘出,受溅水喷流冲击效应影响,Ddisp先振荡增大后逐步减小,变化规律与由式(2)和式(4)绘制的经验公式曲线相一致,且在208 km/h 附近达到最大值,与前2 组结果相差5%以下。因而,本文建立的仿真模型滑水特性得到验证,可再现轮胎滑水前后位移阻力的变化过程。
值得注意的是,当滑行速度超过vP时道面支撑力保持为0,Dfric完全消散,而Ddisp仍处于非线性下降阶段,持续影响飞机姿态和滑行距离,Ddisp更适合作为滑水状态判定依据。
3 积水阻力结果分析
实际道面起降环境复杂,依托本文建立的飞机轮组滑水分析模型,开展不同飞机滑行状态与道面积水分布条件下的积水阻力分析,探讨轮组阻力特征与叠加关系。
3.1 飞机滑行状态影响
飞机着陆过程中轮胎瞬间高速接地开始滚动滑行,在发动机反推和刹车系统共同作用下持续减速直至脱离跑道,轮胎受到积水阻力规律与一般起飞加速过程有明显差异。有统计表明,着陆阶段发生滑水事故几率达到起飞阶段的4 倍[25],滑行状态影响不容忽视。
假定道面覆盖7.6 mm 厚均匀积水,水流以250 km/h 初始速度冲击轮组模型,当轮胎接触面水域完全覆盖并稳定后,降低速度模拟着陆滑行过程,作为起飞加速情况对照,其他参数与2.1 节一致。图7 为不同滑行速度下着陆滑行道面积水分布。

图7 着陆滑行过程道面积水分布Fig.7 Distribution of accumulated water on pavement surface during landing
图7 中上层Eulerian 网格描述流体运动分布,下部规整道面网格为流体变形分析提供参考系。如图7(a)所示,着陆瞬时飞机滑行速度超过vP,轮胎底部可见大量水流通过,积水承托作用使得轮胎与道面脱离,轮胎接触面轮廓不清晰,处于完全滑水状态;当速度降至210 km/h 时,如2.2 节讨论,此时轮胎处于滑水临界状态,轮胎接触面恢复且较为完整,胎纹为流体提供底部排水通道,轮胎前缘及两侧Eulerian 网格“挤密”,积水阻力处于较高水平;随着滑行速度进一步降低,图7(c)中流域已被左右机轮接触面完全分隔,轮胎脱离滑水状态,除轮胎前缘出现雍水外,轮胎外侧及中间轮隙Eulerian 网格变形明显,绕流流体与阻挡水墙冲撞形成侧方喷流。显然,不同于飞机起飞阶段由低速充分接触发展至高速滑水脱离过程,着陆滑行状态可改变轮胎与道面接触条件及积水分布规律。
图8 为不同滑行状态下道面积水阻力,依据式(2)和式(4)对散点数据分段拟合,并以拟合曲线形式绘出。如图中箭头指向,着陆滑行时轮胎所受道面积水阻力经历了反向先增大后减小的变化过程,阻力变化路径与起飞滑行并不重合。相同速度条件下着陆滑行阻力更小,峰值点对应vP更低,超越临界滑水状态概率增加,符合滑水事故统计规律。积水厚度为7.6 mm 时,vP结果相差约8.3%,积水厚度为13.0 mm 时,vP相差增大至10.6%,与文献[25]中给出的15%参考值相接近。
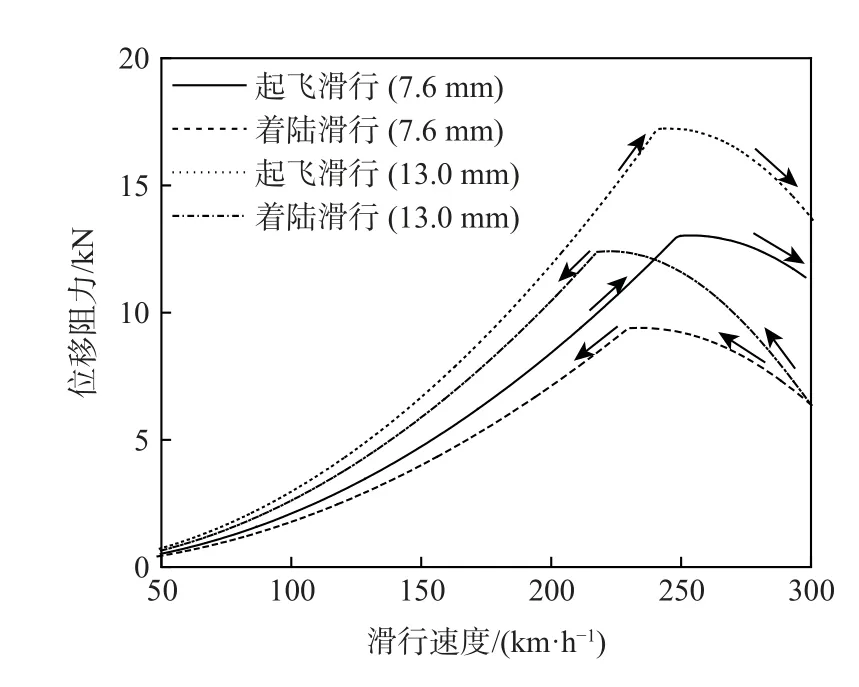
图8 不同滑行状态下道面积水阻力Fig.8 Drag force of accumulated water on pavement surface under different taxing conditions
综合本节所述,飞机滑行状态对轮胎滑水影响不容忽视,积水阻力结果表明:着陆时滑水风险更高,滑水控制条件更严格,后续分析针对着陆滑行条件展开。
3.2 道面积水条件影响
道面积水分布是影响轮胎滑水行为的另一重要因素。当局部轮辙变形形成后,可干扰道面横坡正常排水功能,增大道面积水阻力,引发轮组内部滑水行为差异。
假定环境降雨与道面排水达到动态平衡,流域内平均积水厚度为7.6 mm。以A1 加载荷位为例(见图4),此时轮辙中心最大水深可达19.7 mm,发生局部积水厚度超限。依次对图4 中3 组加载荷位进行滑水分析,每组加载荷位具有独立的轮辙变形与积水特征,并与平整道面情况对照。其他参数与2.1 节保持一致。机轮作用于不同荷位时轮组前缘动水压强分布如图9 所示。
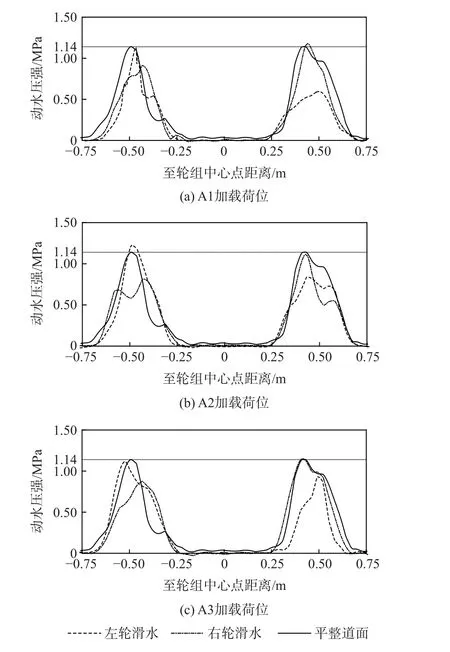
图9 轮胎前缘动水压强分布Fig.9 Distribution of hydrodynamic pressure at tire frontier
由图9 可知:①平整道面条件下积水均匀,轮胎前缘动水压强关于轮组中心点对称分布,左右轮胎压强峰值同时达到胎压等级1.14 MPa,积水阻力挤压轮胎变形,可视为轮胎滑水发生临界时刻,轮组内部滑水进程基本一致;②当轮组作用于A1 加载荷位时右轮积水厚度高于左侧,右轮达到滑水临界时刻时,左侧压强峰值仅为0.92 MPa,而左轮达到滑水临界时刻时,右侧压强峰值已降为0.61 MPa,对照图8 中滑水前后积水阻力变化规律,两侧轮胎并非同时发生滑水;③A2 加载荷位位于轮辙断面大斜率段,整体积水厚度虽低于A1 加载荷位,但两侧积水厚度差加大,左轮积水更厚因而可先于右轮达到滑水临界时刻,图9 中动水压强曲线非对称分布特征显著;④A3 加载荷位位于轮辙断面相对平坦段,整体积水厚度和两侧厚度差均小于A1 和A2加载荷位,动水压强分布非对称性减弱,较平整道面仍有差异。
图10 为不同加载荷位时左右侧轮胎积水阻力变化规律,结果以拟合曲线形式绘出。表2 不同加载荷位临界滑水速度比较结果。可以看出:①在250 km/h以下飞机着陆滑行速度范围内,3 组加载荷位道面积水阻力均高于平整道面情况,阻力曲线上升与下降速率增大,vP结果低于平整道面情况,对飞机滑行安全不利;②除平整道面情况外,3 组加载荷位轮组阻力曲线并不重合,两侧轮胎并非同时发生滑水,符合图9 中动水压强分布规律;③A1 加载荷位覆盖轮辙断面最大深度处,vP结果与平整道面相差最大达到12.8%,且右轮vP较左轮低3.5%;④与A1 加载荷位相反A2 加载荷位左轮vP低于右轮,符合轮辙断面局部变形与积水特征,由于积水厚度差高于其他荷位,轮组内部vP相差达到5.7%;⑤A3加载荷位轮辙变形相对平坦,整体积水厚度略高于平整道面,因而轮组内部vP相差仅为1.1%,较平整道面下降6.8%。
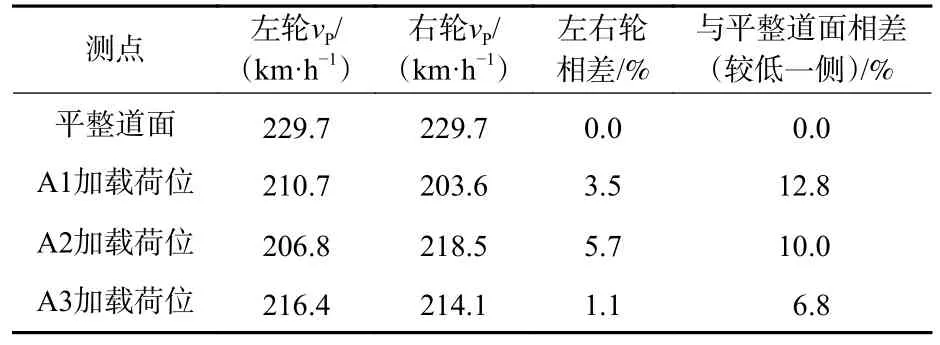
表2 不同加载荷位临界滑水速度比较Table 2 Comparison of hydroplaning speed at different loading positions

图10 不同加载荷位时道面积水阻力Fig.10 Drag force of accumulated water on pavement surface at different loading positions
显然,道面积水条件对轮组滑水影响不容忽视,其内部滑水过程存在时空差异,轮胎前缘动水压强非对称分布,积水阻力变化曲线相互独立。轮辙引起局部积水增厚导致vP降低,滑水风险随之加大。
3.3 轮组阻力特征
对于轮组滑水问题,一般认为由于主起落架轮胎物理间距较大,积水溅水喷流干扰效应有限,对于理想平整道面情况,轮组滑水可近似由单轮滑水行为代表,当起落架构型较简单时,轮组阻力约等于单轮阻力的叠加,式(2)中轮组系数n即为轮胎数量。
如3.2 节讨论,道面积水分布可改变轮组内部滑水行为,影响轮组阻力特征。对此,将单个轮胎阻力结果叠加得出轮组阻力曲线,并与式(2)计算位移阻力理论解求得比值,得出不同加载荷位时轮组系数n随滑行速度的变化规律,如图11 所示。
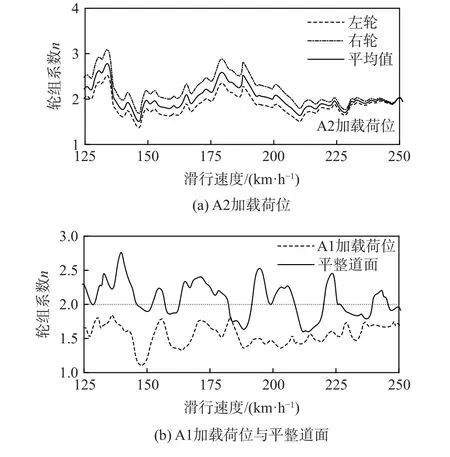
图11 轮组系数随滑行速度的变化曲线Fig.11 Variation cures of wheel configuration coefficient versus taxing speed
如图11(a)所示,分别以左轮、右轮和轮组平均阻力理论解为底,计算轮组系数曲线并进行比较,可以看出当轮组作用于A2 加载荷位时,积水较厚的左轮阻力理论解大于右轮,因而图11(a)中左轮曲线位于右轮曲线下方,曲线变形规律基本一致;由平均阻力曲线计算轮组系数中位数等于1.87,略低于期望值2.0。
如图11(b)所示,在飞机着陆滑行至脱离跑道速度区间内(150~250 km/h),平整道面条件下轮组系数曲线在2.0 上下波动,偏离度不超过2%,轮组系数简化方式基本适用。对比A1 加载不同荷位结果,轮组系数曲线整体在2.0 以下范围波动,实际轮组积水阻力低于式(2)计算理论值。考虑到飞机自动刹车系统,防滑系统和自动扰流系统均以轮胎滑行速度作为激活条件,当轮胎滑行速度未能降低到规定值时,上述3 类措施无法及时发挥减速作用,导致飞机着陆滑跑距离延长,影响飞机着陆安全。
4 结 论
1)轮胎发生滑水前道面积水附加阻力随滑行速度增加而逐步增大,峰值时刻对应轮胎临界滑水速度,与NASA 公式结果相差在5%以下;发生滑水后积水阻力非线性减小,持续影响飞机滑行状态,较道面支撑力更适合作为滑水分析指标。
2)飞机着陆时轮胎与积水道面高速接触可发生瞬时滑水,后随减速滑行脱离滑水状态,影响道面流域特征;相同参数条件下着陆滑行道面积水阻力始终低于起飞滑行过程,着陆阶段临界滑水速度较起飞阶段低8.3%~10.6%,表明飞机着陆过程滑水风险更高,符合事故统计规律。
3)轮辙变形可改变道面积水条件,飞机轮组滑水过程存在时空分布差异,空间上表现为轮组前缘动水压强非对称分布规律,时间上表现为左右轮胎并非同时达到临界滑水状态,vP差值随积水厚度差增加而增大。
4)仅对平整道面理想积水条件,道面积水阻力轮组系数可近似按轮胎数量计算;有轮辙道面条件下轮组积水阻力低于理论值,轮组系数中位数低于2.0,可拖延减速滑行过程,对预防冲出跑道事故较为不利。

