不确定风场下平流层浮空器全局路径规划

翟嘉琪，杨希祥，邓小龙，龙远，张经伦，柏方超

(国防科技大学 空天科学学院，长沙 410073)

平流层浮空器是指依靠轻于空气的气体提供升力，工作于平流层并可实现持久驻空的浮空类飞行器[1-2]，具有成本低、载重能力强、可长期驻空等优点。作为在临近空间开展应用的主要平台，平流层浮空器通过携带任务载荷，具备长时间、全方位、全天时和实时信息获取能力，可以为高分辨率对地观测、预警探测、通信中继、防灾减灾、环境监测等提供技术途径[3]。

目前平流层浮空器的研究主要关注长时驻空、区域驻留等方向[4-8]。例如，Loon 气球已经完成了单球连续驻空335 天23 时的总飞行时间，并能提供网络通信服务的飞行试验[9]，且Loon 团队首次将强化学习应用于气球的飞控系统，并在太平洋赤道附近进行了为期39 天，保持在定点距离50 km 以内区域驻留的验证试验[10]；国内多个机构，如北京航空航天大学、中国科学院空天信息创新研究院、中国电子科技集团第三十八研究所等研究的平流层浮空器也基本具备长航时驻空和区域驻留的能力。针对未来战场的快速变化及平流层浮空器的实际应用场景需求，如何实现从放飞点到目标区域的快速部署，即浮空器的路径规划，将是制约浮空器未来大规模应用的关键问题。

浮空器路径规划是指依靠风场环境和浮空器设计参数，在约束条件下（如能源、动力、时间及距离等），规划从起始点到目标点的最优路径，不同约束条件可以规划出不同的飞行路径。

目前的路径规划大多是针对无人机、水下航行器、机器人及无人驾驶车辆等对象[11-14]，常见的路径规划方法主要分为2 类，即传统路径规划和智能路径规划。其中，传统路径规划中的路线图构建方法简单、易于实现，主要能用于二维路径规划中；单元分解法能完整描述环境信息，但是规划速度与分解的单元个数息息相关；这2 种方法都需要通过搜索方法来寻找最优路径，常见的有A*、D*方法；人工势场法是一种虚拟算法，智能体在环境中受到来自目标点的吸引力势场和来自障碍物的排斥力势场组成的合势场来决定其运动信息，该方法实时性好，计算简单，但是容易出现局部锁死、路径振荡等问题。针对传统路径规划自适应性较差，提出智能路径规划方法，因其源于模拟人的经验或生物的行为，具有自组织、自学习及一定的容错能力，将其应用于路径规划中，可以提高系统的自主能力，使得系统更加灵活，自主性和适应性更强，主要包括遗传算法、神经网络、强化学习及深度强化学习等。

目前针对平流层浮空器的路径规划研究较少，多为无人机等研究对象，通过对比，大尺寸、低动态的平流层浮空器在飞行过程中更易受风场影响，因此，在浮空器的路径规划中可充分利用风场提供推力，同时引入一定的水平弱动力，在风场中可通过规划动作序列，避免部分不利风场影响，快速部署至目标区域。

由于风场环境的不确定性和时空复杂性，基于随机概率的方法是研究浮空器的路径规划问题的合理手段，为此，研究人员针对马尔可夫决策过程（Markov decision process, MDP）方法进行了一定的研究。MDP 是一个描述系统与外部环境之间相互作用的模型，并尝试选择合理的动作使得累积报酬最大，不需要给定任何状态下的监督信号，可以用来处理不确定情况下的规划问题，在路径规划中应用广泛。Wolf 等[15]提出一种基于MDP 的概率运动规划方法，其研究对象是运行在土卫六的Montgolfieré气球（热气球的一种），仿真结果指出该方法可实现Montgolfieré气球在土卫六的全局路径规划。陈魁[16]基于MDP 模型设计了码垛机器人的路径规划，采用最小二乘策略迭代方法设定基函数，求取最优状态-动作值函数，并且基于激光测距仪设计了基于部分可观MDP（partially observable Markov decision process，POMDP）的局部路径规划模型，使机器人具有避障能力。Yu 等[17]针对无人机在恶劣环境下的避碰问题，提出一种基于MDP 的方法，规划出来的无人机路径安全无碰，仿真结果表明，设计出来的路径可有效避免障碍物的攻击，但是该方法并没有将环境的不确定性引入其中，环境信息提前确定，不能很好地满足实际情况。Kularatne等[18]基于MDP 计算在不确定海洋环境下的水下航行器路径规划问题，约束条件是最低能耗和有效避障，仿真结果表明：MDP 方法更适用于起始点和目标点位置固定且不确定性已知的情况。Nanaz 等[19]通过对气球的动力学模型进行简化和解耦，将全局路径规划问题转化为图形搜索问题，使用Dijkstra方法计算给定目标点与土卫六上任意位置的最短时间路径，但是该方法不适用于不确定情况下的路径规划。

本文以具有弱动力的平流层浮空器为研究对象，提出一种基于MDP 的全局路径规划方法。所提方法充分考虑了风场预测模型的误差，并将误差引起的风场不确定性引入MDP 模型中，建立浮空器的二维全局路径规划模型。

1 问题描述及基本假设

由于平流层浮空器在长期驻空过程中的运动多为二维平面运动，本文对基于MDP 的浮空器全局路径规划方法有以下4 个假设。

1）不考虑浮空器垂直方向的运动。

2）浮空器吊舱四周安装4 个相互独立的动力设备（电机和螺旋桨）为其提供水平驱动力，单个动力设备能提供的最大速度umax=5 m/s，浮空器最多允许2 个动力设备同时工作。

3）浮空器无动力时的速度与风速一致，即处于随风飘飞的状态。

4）不考虑浮空器的动力学特性，只考虑其运动学特性。

本文研究区域在我国某地区，浮空器在该区域内的位置用r≜[x,y]表 示，其中x为 经度，y为纬度，风 速 用w(r,t)≜[wx(r,t),wy(r,t)]表 示，其 中wx(r,t)和wy(r,t) 分 别表示在t时刻x轴 （东西方向）和y轴（南北方向）的风速大小。在给定区域内，以∆x=0.3◦,∆y=0.3◦为精度进行离散化，得到如图1所示的21×21栅 格区域。针对栅格i，si表示浮空器的状态信息，ri表示浮空器在状态si下 的位置，w(ri,t)表示风场信息。

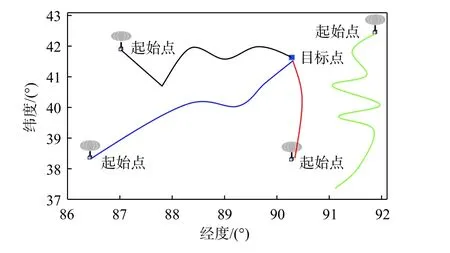
图1 区域离散化示意图Fig.1 Diagram of regional discretization

在风场的作用下，浮空器的速度v(si)=w(ri)+u(si)，其中u(si)表 示浮空器在状态si下自身所能提供的速度。针对栅格i，si表 示当前状态，sj表示下一状态，风场信息从状态si到 达临近状态sj的过程中始终保持为w(ri)，到达状态sj时才更新为w(rj)。在目标点确定时，位于给定区域内任意位置的浮空器在风场和自身动力的共同作用下向目标点靠近，但是有的位置在共同作用下始终无法抵达目标点，而某些位置可以在很短的时间内到达目标点，如图1 所示，即本文重点研究的区域可达性和最短时间的最优路径问题。

定义浮空器的移动方向为正北、东北、正东、东南、正南、西南、正西、西北8 个方向，将360°平均分为8 个部分，如图2 所示，其中，θi j为由状态si进 入相邻状态sj将空间分成8 个部分的较小边界角度。

图2 浮空器状态转移方向Fig.2 Transition direction of a stratospheric aerostat

2 相关方法模型

2.1 马尔可夫决策过程

MDP 是一种描述智能体和外部环境之间相互作用的模型，如图3 所示，常被用来作为序列决策问题的框架，可以用一个五元组M=(S,A,P,R,γ)来表示[14]，S代表环境状态的集合，A代表智能体能执行的基本动作集合，Pa(s,s′)表 示智能体在状态s下执行动作a到 达状态s′的 概率，Ra(s,s′)表示智能体在状态s下执行动作a到 达状态s′所得到的即时奖励，γ表示折扣因子，取值范围为 [0,1]，γ越大表示后续奖励对当前奖励的影响越大。

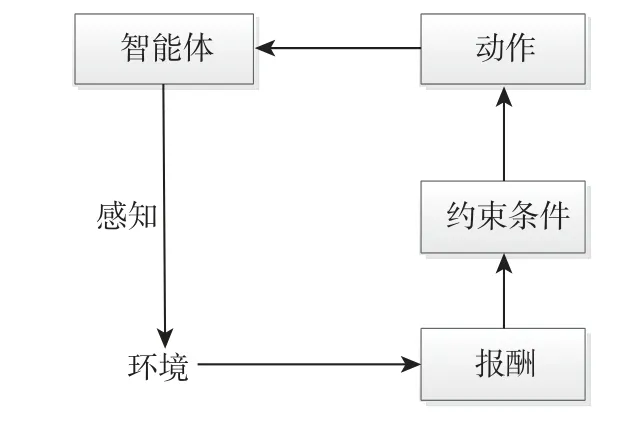
图3 MDP 模型Fig.3 Model of Markov decision processes

当MDP 用来表示序列决策问题时，决策问题的解即为策略（π），是从状态集合到动作集合的映射，即 π:S→A，求解MDP 即可表示为求解最优策略（π∗）的问题，即浮空器在所处状态采取的最优动作，使得所获得的累积奖励最大。累积奖励可形式化表示为浮空器所处状态的价值（状态-值函数）：

式中：Vπ(s) 为 执行策略 π后 在状态s下 的价值；t为决策时刻；Rt为t时刻下的即时奖励。

对于任意状态，使得值函数最优的充要条件是Bellman 方程，最优策略 π∗是使得值函数取得最大值时的策略：

式中：π∗(s)为 智能体在状态s下的最优策略。

求解最优策略常见的方法有策略迭代和值迭代[20]，其中策略迭代需在每个状态-值收敛后再进行策略提升，不断地迭代直到策略收敛，而值迭代在状态-值每更新一次之后进行策略提升，再重复进行状态-值更新和策略提升直至状态-值收敛[21]。因值迭代方法在本文研究的问题中具有更高的计算效率，本文采用值迭代方法进行求解。

2.2 二维风场分布

在实际情况下，风场数据为该区域内的各个离散气象站提供的预测数据，在考虑风场因素时直接把某个气象站的数据作为该区域内的整体风场数据，风向、风速只随高度变化，不会对该区内各个高度的二维风场分布进行处理，但是在实际路径规划中，必须考虑二维风场的空间分布。本文根据各个气象站的风场预测数据，采用双线性差值法如图4 所示，根据各点距离气象站的距离确定权值，可以得到该区域内各个高度的二维风场分布，具体步骤如下：

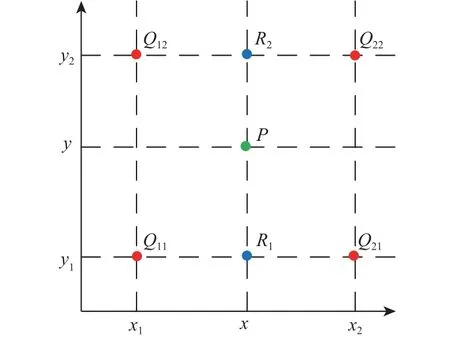
图4 双线性差值法示意图Fig.4 Diagram of bilinear interpolation method

1）二维线性差值。按照双线性差值法如式（4）所示，可以得到二维区域内任意位置的数值。

式中：（x1,y1）、（x1,y2）、（x2,y1）、（x2,y2）、（x,y）分别为Q11、Q12、Q21、Q22、P的位置坐标。

2）确定权值。由于区域中各个点的风速风向与每个气象站的实际数据有关，即目标点距离某个气象站越近，该点的风速风向越接近该气象站的实际数据，如图5 所示，因此，目标点的气象数据与各个气象站在该点的权值有关，将其设置为与气象站的距离成反比，为目标点与气象站的水平距离，权值按照式（5）取值。

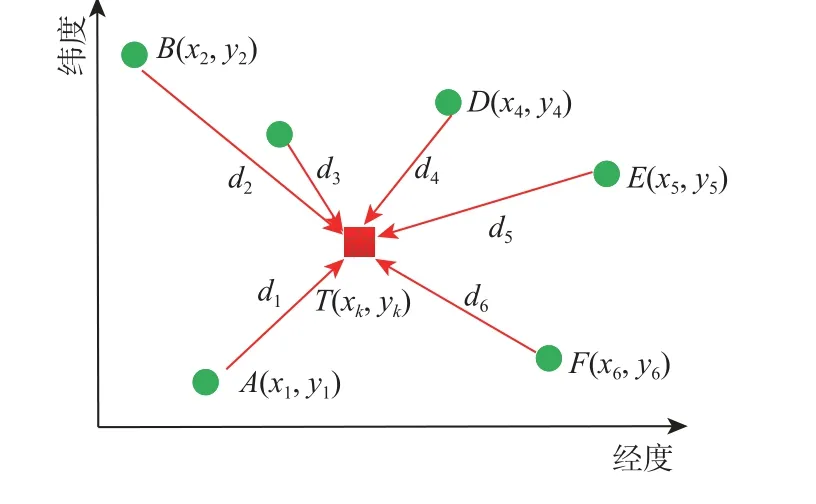
图5 二维平面权值确定示意图Fig.5 Diagram of determination of two-dimensional plane weights

式中：η为 权值；(xk,yk)为 待求目标的位置坐标；d为待求目标与已知点之间的距离；N为气象站点数量。

3）二维风场可视化。二维风场速度的大小通过箭头的长度和颜色表示，箭头越短，颜色越蓝，风速越小；风向通过箭头的指向来表示，箭头的方向即为风的来向。为了和浮空器的状态数量保持一致，二维风场分布也划分为 21×21个栅格。如图6所示。

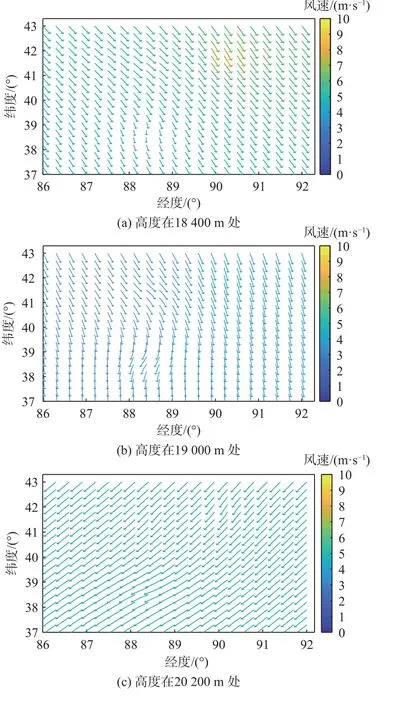
图6 不同高度的二维风场分布对比Fig.6 Comparison of two-dimensional wind field distribution at different heights

2.3 不确定风场模型

由于风场模型可能存在的不准确性，风场数据存在一定的误差，为了使得路径规划更加符合实际情况，本文将不确定性引入风场中，建立不确定风场模型。风场信息包括风向和风速，分别用 θi和wi表示，两者具有相互独立的概率分布，风速和风向由w(ri)表示[15]。

1）风向概率分布。风向概率分布采用von Mises 分布，该分布是圆上的连续概率分布，近似于包裹正态分布，是正态分布的圆形模拟，概率密度函数为

式中：θi=∠w(ri)为可获得的风场数据中的实际风向，整个分布围绕它展开，取值范围为 [0◦,360◦]，其中正北风向为 0◦（3 60◦），正东方向为 90◦，以此类推可以得到所有风向对应的角度；κ为风向分布的集中程度，κ＞0，且 κ →0，分布越分散，κ →∞，分布越集中；I0(κ)为0 阶Bessel 修正函数。

2）风速概率分布。风速概率分布采用Gaussian分布，其概率密度函数为

式中：σi=ρwi，wi=//w(ri)//，w(ri)为可获得的风场数据中的实际风速，整个风速分布围绕它展开；ρ为分布幅度的参数，可按实际情况取值。

根据实际风场数据，在19 000 m 高度、37°经度、86°纬度处，风向 θi=251.916◦，κ=1/400，风速wi=[0.344 6,−3.559]，ρ=0.2，可以得到该点处的风向、风速的概率分布，如图7 所示。

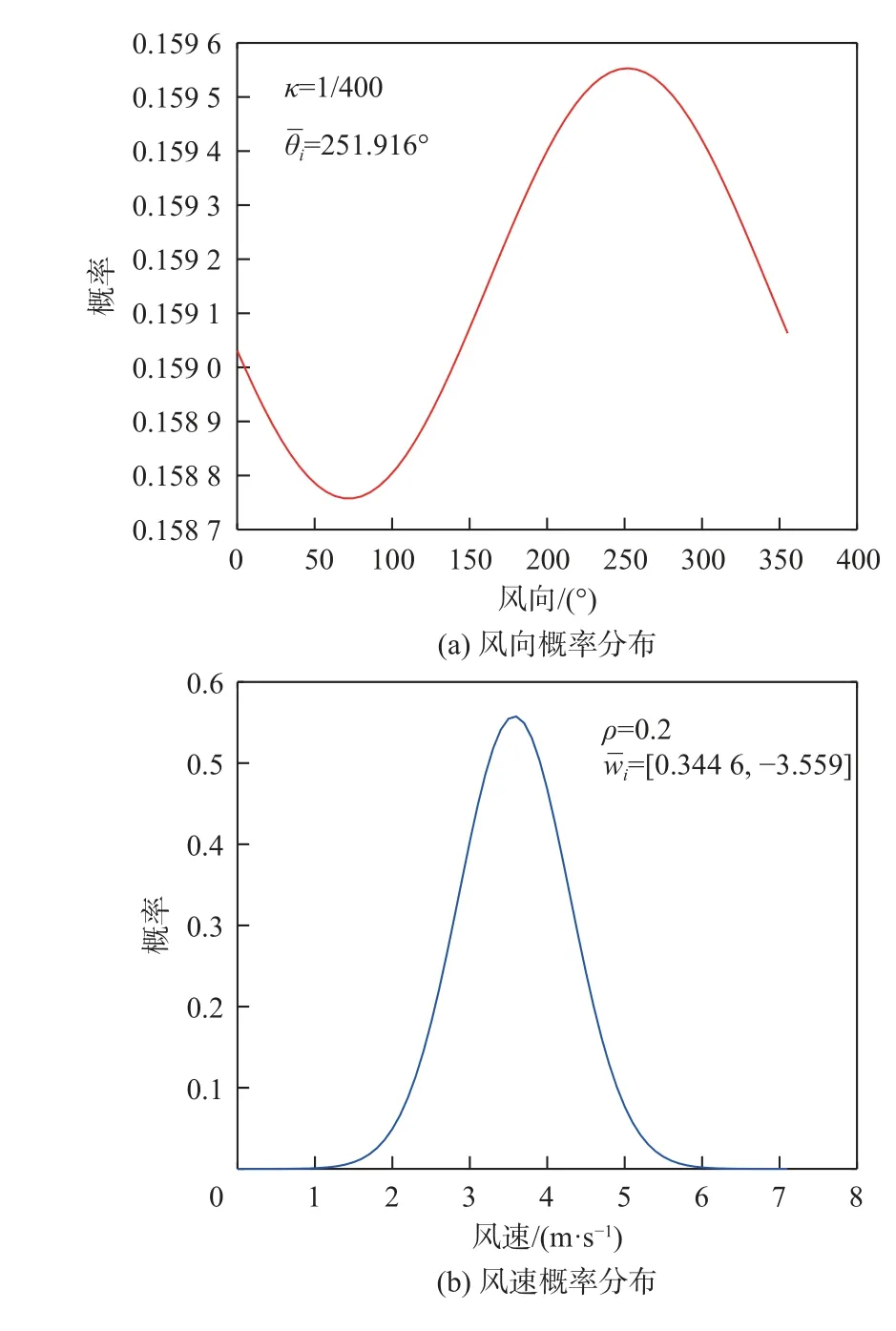
图7 不确定模型下风向和风速概率分布Fig.7 Probability distribution of wind direction and speed under uncertain model

3 基于MDP 的全局路径规划

3.1 MDP 模型中关键参数设计

1）环境状态集合S。本文浮空器所处区域，经过离散化得到 21×21个栅格，MDP 模型中的状态S即为 21×21个栅格中的风速和风向。由于风向的范围为 [0◦,360◦]，按照图3 中对角度和方向的划分，风向可分为如下8个方向，分别为：①正北：[0◦,22.5◦]∪[337.5◦,360◦]；②东北：[22.5◦,67.5◦]；③正东：[67.5◦,112.5◦]；④东 南：[112.5◦,157.5◦]；⑤正 南：[157.5◦,202.5◦]；⑥西 南：[202.5◦,247.5◦]；⑦正 西：[247.5◦,292.5◦]；⑧西北：[292.5◦,337.5◦]；

当风场中的风向数值确定之后，浮空器在无动力情况下的移动方向就确定为这8 个方向之一。

2）基本动作集合A。浮空器自身的速度由4 个相互独立的动力设备提供，且最多允许2 个设备同时工作，通过控制动力设备的开启和关闭，可以得到9 个基本动作，正东方向为x轴正方向，正北方向为y轴正方向，浮空器基本动作方向如图8 所示。动力设备均不工作，浮空器无动力：[0,0]m/s。

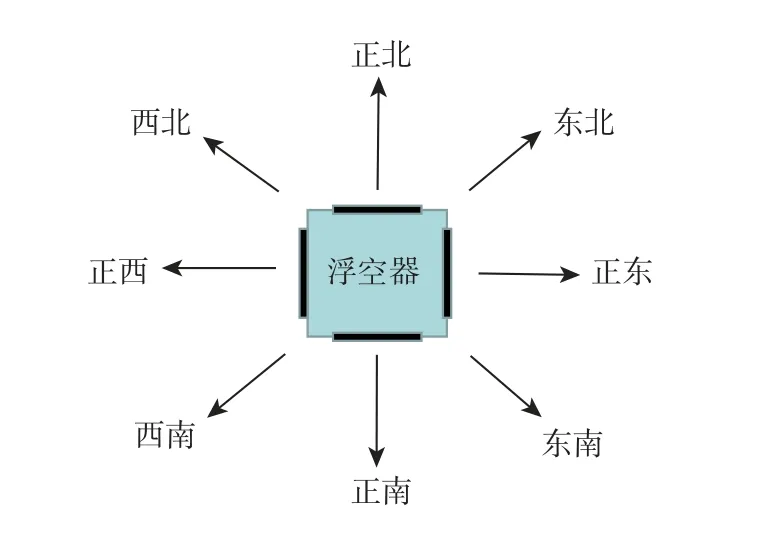
图8 浮空器基本动作方向Fig.8 Basic action direction of stratospheric aerostat

只有1 个动力设备工作，浮空器分别具有向正北、正东、正南、正西方向的速度，通过调整动力设备使得浮空器可具备5 m/s 和2 m/s 的速度，速度大小为：[0,5]，[5,0]，[0,−5]，[−5,0]，[0,2]，[2,0]，[0,−2]，[−2,0]m/s。

2 个动力设备同时工作（本文假设2 个设备所能提供的速度一致），浮空器分别具有向东北、东南、西南、西北的速度，通过调整动力设备使得浮空器在单个方向可具备5 m/s 和2 m/s 的速度，此时速度大小为：[5,5]，[5,−5][−5,−5]，[−5,5]，[2,2]，[2,−2]，[−2,−2]，[−2,2] m/s。

3）转 移 概率P。Pa(si,sj)表 示浮 空 器 在状 态si下 通过采取某个动作a进 入到状态sj的概率。转移过程中包括2 种模型：一种是确定模型，即浮空器在风速和自身驱动速度的共同作用下，从初始状态si转 移到的唯一确定的临近状态sj；另一种是不确定模型，即由于风场的不确定性，导致浮空器在不确定的风速和自身驱动速度的共同作用下，从初始状态si转 移到的临近状态sj是不确定的，是具有一定的概率的。在浮空器无动力的情况下，风向分布决定浮空器的转移概率为

浮空器在无动力、速度为 [5,5]m /s 及 [−5,−5]m/s情况下的转移概率分布情况如图9 所示。

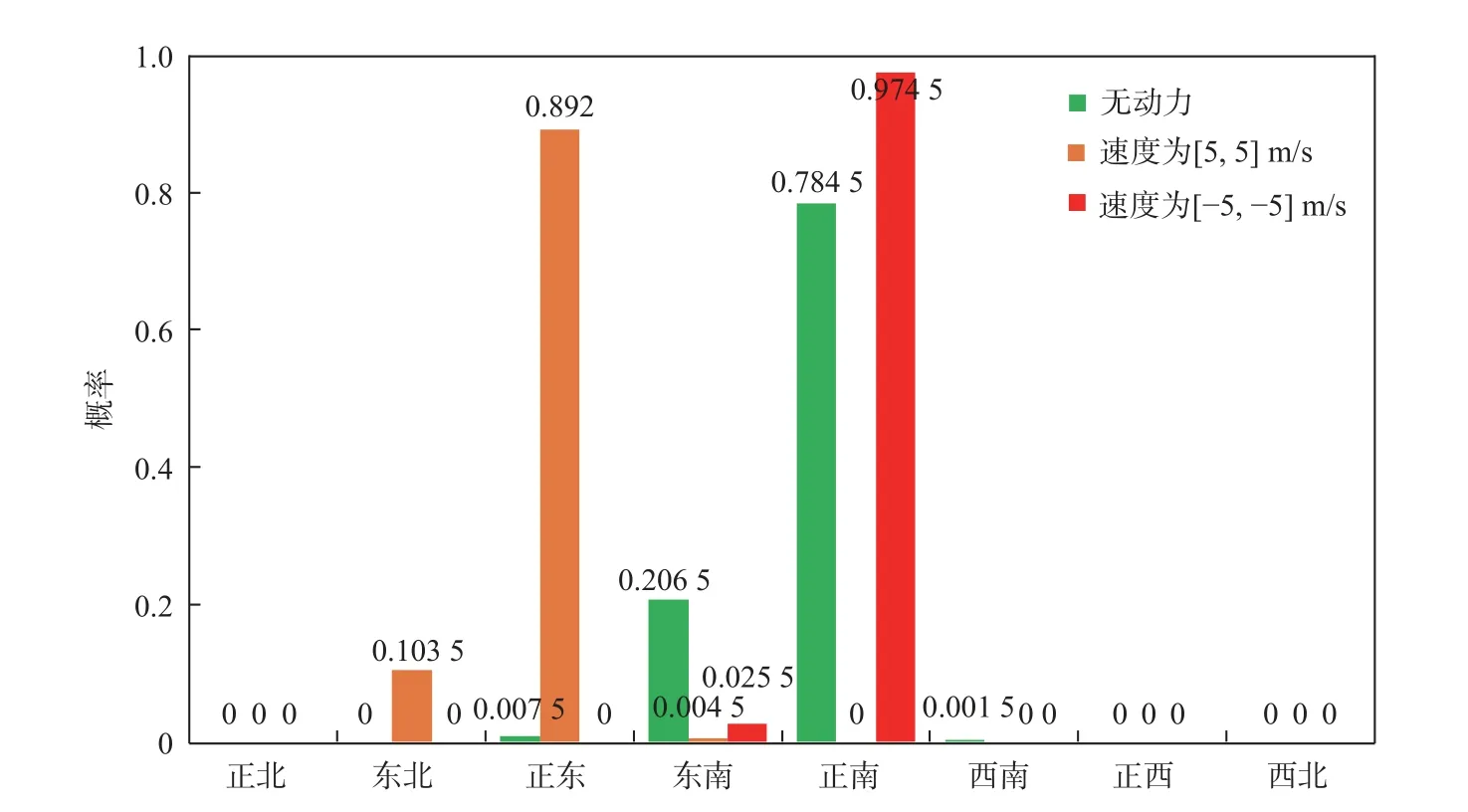
图9 不确定风场下浮空器转移概率分布Fig.9 Transition probability distribution of stratospheric aerostate under uncertain model

4）奖励函数R。为描述浮空器状态、动作和目标之间的关系，奖励函数用Ra(si,sj)表示，具体含义为浮空器在选择动作a的情况下由状态si转移到状态sj所 消耗时间的负值，奖励函数R为即时奖励，且共有 21×21×9个 数值。浮空器在由状态si移动到sj过 程中所消耗时间为 δt，则Ra(si,sj)=−δt，如下：

式中：dist(·,·)为 2 个栅格间的实际距离；vi,a为浮空器实际速度矢量，由风速和浮空器自身速度合成，vi,a=w(ri)+ua；w(ri)为 风场在位置ri处的矢量风速；u(si)为 浮空器在状态si下所能提供的速度。

路径规划目的是使浮空器在给定区域内找到一条从起始点到目标点飞行时间最短路径，因此，奖励函数需考虑到距离区域边界、远离目标点、趋向目标点等所有情况，在确定风场下的奖励函数为

式中：Ra(si,sj)表示浮空器分别在转移过程中趋向目标点、远离目标点及超出区域边界时的即时奖励，式（14）情况相同。

在不确定风场下，由于风场信息的不确定导致浮空器的实际速度也无法确定，本文用均值来表示浮空器在状态si下 通过采取动作a得到的平均速度，此时相邻2 个状态的飞行时间为

由于风场的不确定性，导致浮空器由状态si进入到相邻状态的sj也是无法确定的，通过不确定风场的转移概率，不确定风场下的即时奖励根据飞行时间期望值来确定，而飞行时间的期望值则根据转移概率计算：

3.2 值迭代方法

本文中的风场模型包括确定风场和不确定风场2 种模型，因此，值迭代方法也分为2 种，在确定风场下，浮空器选择动作后到达下一状态是确定的；而在不确定风场下，浮空器选择动作后到达下一状态具有一定的概率，区别在于状态转移概率Pa(si,sj)如何求解，值迭代方法步骤如下：

步骤1输入环境状态、基本动作集合、即时奖励、转移概率、目标点位置，并初始化状态值函数。

步骤2计算所有环境状态下确定风场和不确定风场下的状态值函数。

步骤3计算2 次状态值函数的差值。

步骤4若差值达到值迭代收敛阈值，则末次计算的值函数即为最优状态值函数，若未达到，则返回步骤2，迭代次数增加1 次。

步骤5若迭代次数大于最大迭代次数，则末次计算的值函数即为最优状态值函数，若未达到，则返回步骤2，迭代次数增加1 次。

3.3 路径规划流程

全局路径规划流程见图10。实现步骤如下：

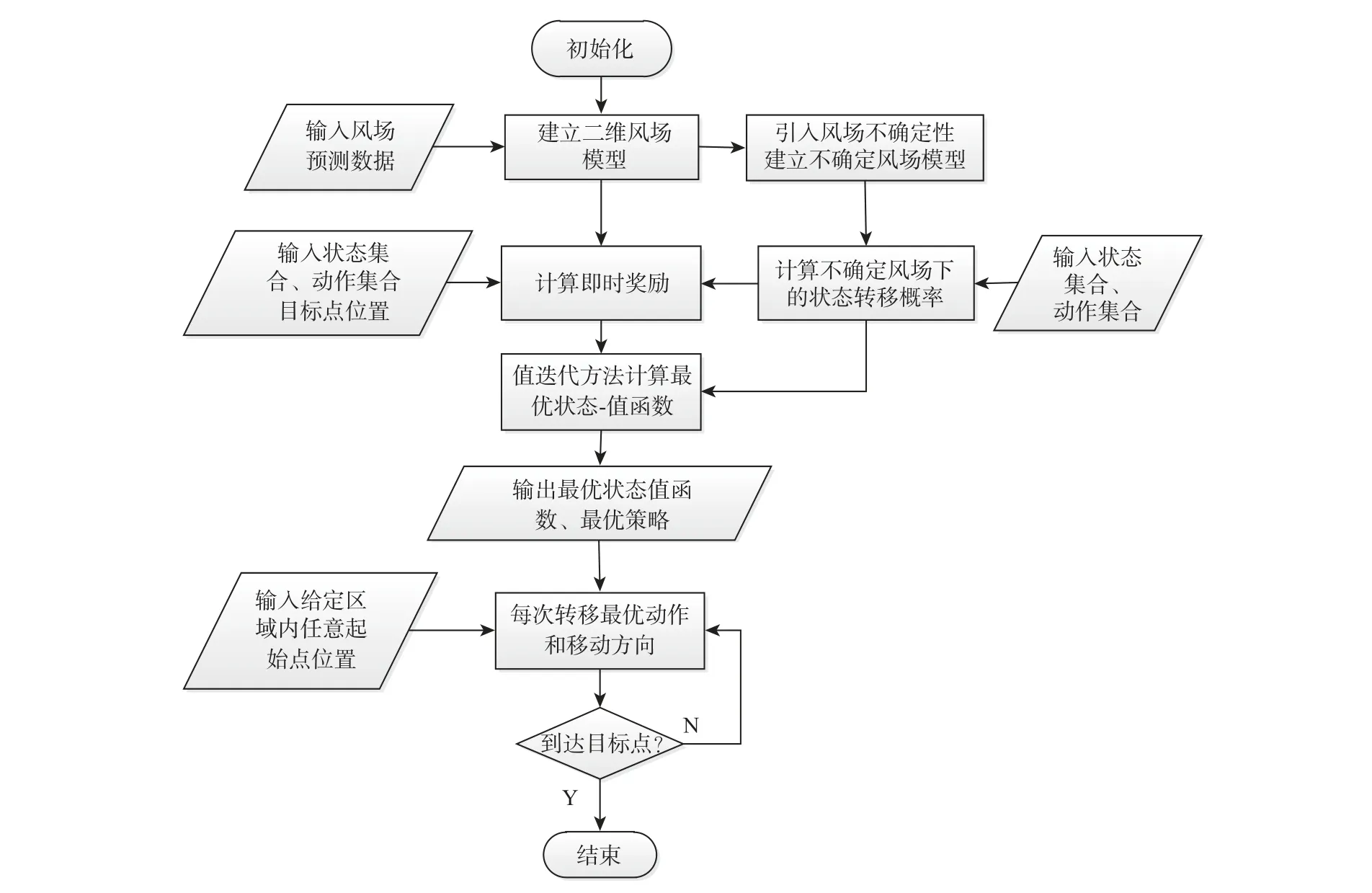
图10 全局路径规划流程Fig.10 Flowchart of global path planning

步骤1初始化参数。

步骤2以风场预测数据为输入，建立二维风场模型。

步骤3针对风场不确定性，建立二维不确定风场模型。

步骤4以状态集合、动作集合为输入，计算状态转移概率。

步骤5以状态集合、动作集合、目标点位置为输入，计算2 种风场模型下的即时奖励。

步骤6根据浮空器的即时奖励和转移概率，用值迭代方法计算浮空器的最优状态值函数，并输出最优状态值函数和最优策略。

步骤7以飞行区域内任意位置为起始点，根据最优状态值函数，获得每次转移的最优动作，结合风场得到转移方向。

步骤8判断是否到达目标点，若到达，则结束流程，若未到达，则返回步骤8。

4 仿真结果分析

将第3 节中的模型和方法应用于浮空器的全局路径规划，通过在MATLAB2020a 环境下建立的模型进行仿真，验证参数设计和方法流程的有效性和工程实用性。

4.1 区域可达性仿真结果分析

在实际任务中，当给定目标点时，浮空器需要快速机动部署至目标区域实施任务，但是由于浮空器自身载荷能力、动力设备等限制，导致浮空器的驱动速度不高，抗风能力较弱。在没有动力甚至在有一定动力的情况下，若浮空器自身驱动能力无法补偿风场的不利影响，也会导致浮空器在某些位置无论采取何种动作均无法达到目标点。

本节主要对浮空器自身驱动速度与给定目标的可达性之间的关系进行分析，使用的是中国某地区的6 个气象站点的气象数据，按照第2 节中的方法得到19 000 m 高度的二维风场分布，给定目标点为[88.7◦,41.2◦]，图11 中白色方框所在位置，图11 和图12 分别为在确定风场和不确定风场的情况下，在无动力、单个动力设备提供的最大速度umax=2 m/s、umax=5 m/s时，浮空器在区域内任意位置到达给定目标的期望时间。

图11 确定风场下不同最大抗风能力期望到达时间分布Fig.11 Distribution of expected arrival time at different speeds in certain wind field

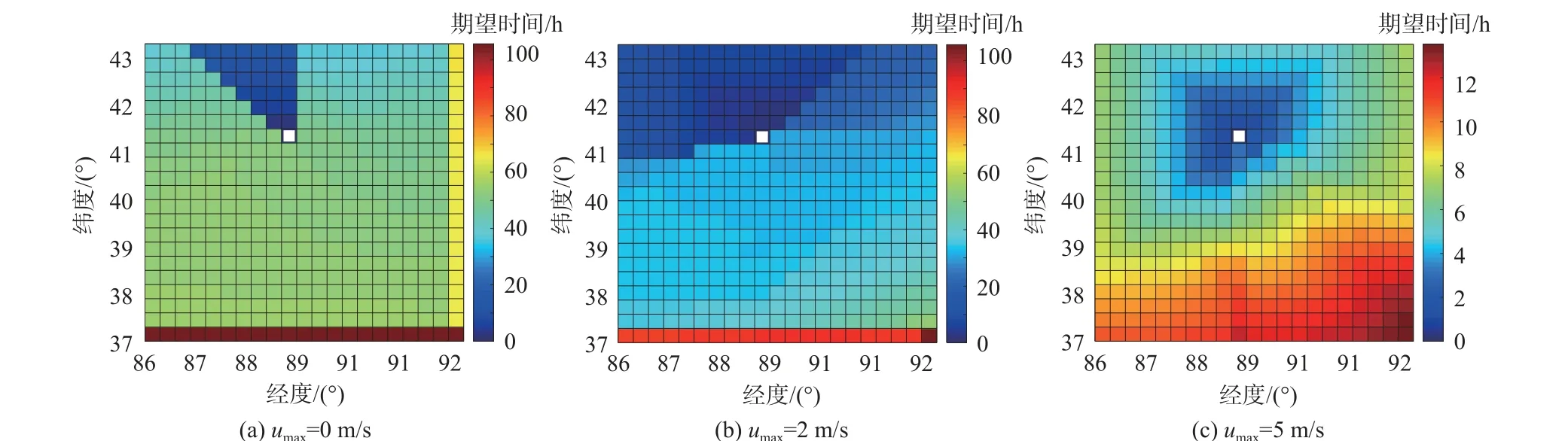
图12 不确定风场下不同速度期望到达时间分布Fig.12 Distribution of expected arrival time at different speeds in uncertain wind field

1）确定风场模型。在确定风场模型下，浮空器在每个状态下的移动方向由该状态下的风速、风向及浮空器自身提供的速度唯一确定。图11 和图12中栅格的颜色表示到达目标点的期望时间，颜色越红到达时间越长，根据19 000 m 高度处的风场分布可知以北风分量为主，西风分量较小。当浮空器无动力时只能通过风场的作用到达目标点，只有在特殊几个栅格状态下可以快速部署到目标区域；当浮空器的单个动力设备提供最大速度为2 m/s 时，浮空器在某些位置下期望到达时间为100 h，当某些位置的期望到达时间过大时，在实际情况下可将其定义为不可到达点，即起始点不可选在这些位置；当浮空器的单个动力设备提供最大速度为5 m/s时，浮空器在给定区域内的大部分位置到达时间在10 h 以内，只有极少数的状态下期望到达时间为14 h，该区域内的任意点均可作为起始点。

2）不确定风场模型。在不确定风场模型下，浮空器的实际速度和实际转移方向是按照一定的概率进行分布的，通过Mont Carlo 方法统计得到风场的分布概率，由图12 可知不确定风场与确定风场相比，期望时间的分布规律大致相同，风场按照第2 节中的概率分布，导致浮空器在转移到临近状态时存在不确定性，根据转移概率和即时奖励（相邻2 个状态之间的飞行时间）来确定状态值函数。随着浮空器自身提供的驱动速度增加，给定区域内的各个位置可到达给定目标点的数量增加，因此，浮空器的水平驱动速度可改变区域内各位置相对于给定目标点的可达性。

3）2 种风场模型的对比。由图11 和图12 可知，当浮空器无动力时，对于给定目标点，不确定风场模型下较为合理期望到达时间占据栅格更多（蓝色栅格），确定风场模型下不可达的栅格数量更多（红色栅格）；但是随着浮空器水平驱动能力的加强，确定风场模型下蓝色栅格的分布和数量与不确定风场模型下蓝色栅格的分布和数量逐渐一致，说明浮空器的水平驱动能力可以抵消一部分风场不确定的影响。

4.2 最优路径规划仿真结果分析

本文规划的路径为最短时间路径，浮空器在到达目标点的过程中需不断根据实际风场来选择最优动作序列，使其能够在最短的时间内快速机动至目标区域。通过对浮空器在区域内各个位置的期望到达时间的分析，可以找到状态转移的最优方向，去除风场的作用，即可得到浮空器在不同驱动速度下的最优动作序列，浮空器在实际飞行中可按照最优动作序列控制执行机构作动，为浮空器的飞行决策提供指导。

图13 和图14 分别为确定风场和不确定风场下浮空器在不同起始点、不同速度下的最优动作序列和规划出来的路径。目标点的经纬度坐标设置 为 [88.7◦,41.2◦]，起 始 点 经 纬 度 坐 标 设 置 为：[86.3◦,42.4◦]、[90.8◦,37.3◦]，浮空器单个动力设备提供的最大速 度umax=2 m/s 、umax=5 m/s。图13 和图14 中的黑色箭头为该位置下浮空器的最优速度方向，红色箭头为风向，在不确定风场中，红色箭头的长短表示风场分布在该方向的概率大小。

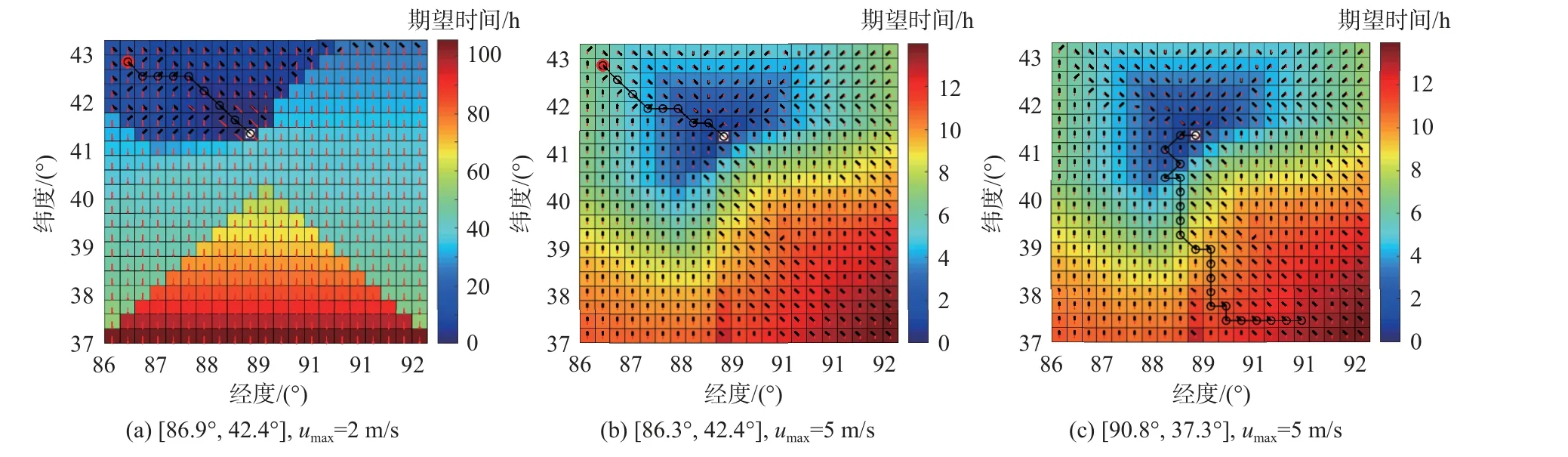
图13 确定风场下路径规划和最优动作序列Fig.13 Path planning and optimal velocity sequence in certain wind field

图14 不确定风场下路径规划和最优动作序列Fig.14 Path planning and optimal velocity sequence in uncertain wind field

浮空器自身的驱动能力、起始点的位置及风场模型均会影响浮空器最优策略即最优动作序列的选择。图13（a）和图14（a）中，当浮空器单个动力设备能提供的最大速度为2 m/s 时，有的位置没有黑色箭头，说明在这些位置无论浮空器采取何种动作，都无法到达靠近目标点，因此，在浮空器实际飞行过程中应该避免到达这些位置；但是当浮空器单个动力设备能提供的最大速度为5 m/s 时，浮空器能够在比较短的时间内到达目标点，相同位置下，由于浮空器自身速度的改变导致浮空器在整个区域的可达性也发生改变；对比图13（b）、图13（c）和图14（b）、图14（c）针对同一起始点和目标点规划的路径，在不确定风场下的路径转弯的次数更少，由于风场的概率分布，浮空器的实际速度也存在概率分布，导致在不确定风场下浮空器的路径规划更符合实际情况。

本文所提方法是在对整个风场环境和浮空器状态空间进行有效的离散化的基础上开展的，与基于图搜索的路径规划方法有一定的相似之处。Dijkstra 方法是其中比较常用的路径规划方法，主要通过搜索空间来求解最优路径，因此，搜索效率不高，尤其是在不确定风场下的路径规划问题，不适用于本文的研究背景。

5 结 论

1）本文所提方法能够在不确定二维风场环境中规划出一条针对目标点的最短时间路径，并能给出给定区域内各个位置下的最优动作序列和期望达到时间，为浮空器的实际飞行执行机构作动策略提供理论依据。

2）本文所提方法还可提供浮空器在不同水平驱动能力下针对目标点的区域可达性，为后续浮空器的飞行策略提供指导。