基于分层优化的多源融合定位方法

刘傲，修春娣

(北京航空航天大学 电子信息工程学院，北京 100191)

行人精确连续定位是复杂室内环境下位置服务、应急疏散、智能管理等应用领域共同关注的问题。随着智能便携终端的普及，基于地磁、Wi-Fi、视觉、超宽带及惯导等定位源的定位技术得到了广泛应用[1-3]。然而，单一定位源由于自身特征上的局限性，往往难以满足行人连续定位的精度需求。例如，地磁在特征相似区域易产生误匹配，Wi-Fi 动态定位可能产生信号堆积，行人航位推算(pedestrian dead reckoning, PDR)定位存在误差累积[4-5]。因此，多源融合室内定位逐渐成为研究热点。

目前，国内外在多源融合室内定位方面展开了较多研究。文献[6]提出基于双层级联架构的滤波融合算法。在下层结构中，利用卡尔曼滤波(Kalman filter, KF)获取行人的航向及步长信息，并引入零速修正和非完全约束对惯导进行初步校正。在上层结构中，利用下层传递的信息进行PDR 定位，并将定位结果和地图利用辅助粒子滤波(particle filter, PF)进一步融合。仿真结果显示，当PF 中设定的粒子数能够使定位精度与计算负载两者之间达到平衡时，行人的平均定位误差为1.67 m。为了改善滤波性能，文献[7]提出一种基于 改 进 扩 展 卡 尔 曼 滤 波(extended Kalman filter,EKF)的融合算法，利用Wi-Fi、PDR 与地磁间的相互关系建立三级质量控制机制，对融合过程中的不可靠观测量和不匹配搜索空间进行滤除。该算法在一定程度上降低了定位误差，但代价是算法复杂度的显著提升。文献[8]提出一种基于滤波与因子图的融合方法，利用EKF 融合惯导与里程计信息实现位姿估计，随后结合Kinect 传感器数据送入即时定位与地图构建(simultaneous localization and mapping, SLAM)框 架 进 行 融 合，实验结果表明，该方法提高了导航系统的可靠性与实用性。除了滤波和因子图融合方法，近年来，伴随机器学习技术的发展，神经网络在多源融合室内定位中的应用逐渐得到了更多关注。文献[9]提出一种包含深度卷积神经网络的融合定位方法，采用神经网络进行图像匹配定位，同时利用定位结果约束地磁匹配范围，随后利用PDR 对结果进一步修正。该方法在普通光照场景下的平均定位误差为1.46 m，但由于定位精度还受到相机分辨率影响，在低光照场景下该方法的定位性能较为受限。为了优化定位性能，文献[10]提出了一种基于粒子群优化(particle swarm optimization,PSO)与 极 限 学 习 机(extreme learning machine,ELM)神经网络的双层融合算法，同时引入静态反馈对惯导进行校正，该算法在一定程度上降低了定位误差。

本文提出了一种基于分层优化的多源融合定位方法。利用Wi-Fi 定位结果约束地磁匹配范围，优化地磁定位可能存在的误匹配问题；将集成学习引入神经网络，并利用PSO 减少算法耗时；为了降低Wi-Fi 信号堆积导致的定位误差，利用PF 将上述融合结果与PDR 定位结果进一步融合。由此，实现分层优化的多源融合定位。

1 基于Wi-Fi 约束的地磁定位方法

选用静态采集方式构建Wi-Fi 与地磁指纹库。采用指纹法实现Wi-Fi 定位，进一步利用Wi-Fi 定位结果约束地磁。

将定位场景划分为若干网格，在各网格顶点重复采集多组Wi-Fi 信号强度(received signal strength indication, RSSI)数据，计算信号强度均值并与对应网格顶点的坐标组合，构成对应点的Wi-Fi 指纹序列。地磁数据的采集利用手机内置的磁传感器完成，由于x，y，z三轴的磁场强度会随着手机的位姿变化，但三轴的合磁场强度不会随之改变，因此，将合磁场强度作为地磁指纹，进行克里金插值获得细粒度的地磁全局基准图。

室内地磁特征相对稳固，但不同区域的地磁特征可能相似，实际定位时可能存在较大的误匹配概率。为有效解决这一问题，采用基于Wi-Fi 约束的地磁匹配定位方法，如图1所示。图中Ra为约束区域半径，其值为Wi-Fi 的平均定位误差，由定位场景中对大量坐标已知的静态测试点进行k 邻近（knearest neighbor，k-NN）算法定位的方式获得。在约束区域内进行地磁匹配，有效降低了地磁定位的误匹配概率。

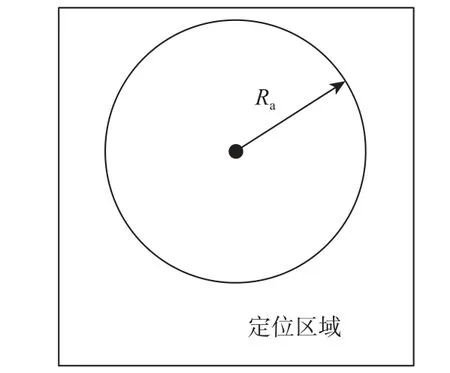
图1 基于Wi-Fi 约束的地磁定位方法Fig.1 Wi-Fi constraint-based geomagetic positioning method

2 基于PSO 优化的BP-AdaBoost 算法

后向传播(back propagation, BP)神经网络属于监督式学习算法。进行样本训练时，通过反向传播方式不断调整网络的权值和阈值，最终达到设定迭代次数或误差小于设定值时停止训练[11]。BP 神经网络的拓扑结构图如图2 所示。图中 γi和 εj分别为神经网络的输入值和预测值。在实际训练过程中，单一BP 神经网络易陷入局部最优，可能导致预测值 εj的精度下降。

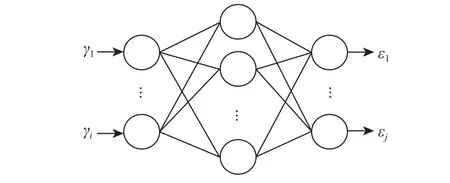
图2 BP 神经网络拓扑结构图Fig.2 Topological structure of BP neural network

2.1 BP-AdaBoost 算法

为提高任意学习算法的预测精度，Freund[12]将集成学习领域的Boosting 算法进行改进，提出AdaBoost 算法。该算法的核心思想是，在迭代过程中更加关注预测错误的样本，迭代结束后，将多个弱学习器按照某种结合策略生成强学习器，利用强学习器进行预测并输出预测结果。

将BP 神经网络作为AdaBoost 中的弱学习器，利用BP-AdaBoost 算法融合Wi-Fi 定位结果与约束后地磁的定位结果，其主要步骤如下。

步骤 1划分数据集与初始化

将数据集划分为训练集、验证集和测试集。其中训练集包含s个训练样本，将第i个训练样本的初始权重wm,i设为

式中：m为弱学习器轮数。

BP-AdaBoost 的输入与输出分别为

式中：Xa和Ya为 Wi-Fi 定位结果；Xb和Yb为约束后地磁的定位结果；Xe和Ye为融合定位结果。

根据BP-AdaBoost 的输入输出维数确定弱学习器结构，并通过随机设定的方式初始化弱学习器的权值和阈值。

步骤 2计算弱学习器的定位误差率与权重

当第m轮弱学习器Hm训练时，每个训练样本的相对定位误差为

式中：Xr和Yr分别为待定位点的真实位置坐标；Em为该轮训练中训练样本的最大定位误差，其表达式为

则第m轮弱学习器的定位误差率为

由于BP 神经网络属于样本无法带权重的弱学习器，因此，需利用wm+1,i对训练样本进行重采样的方式实现实际更新过程。

步骤 4生成强学习器

达到设定迭代次数T后，将T轮弱学习器按照结合策略生成强学习器G。选取的结合策略为加权平均法：

式中：M为弱学习器总轮数。

G的输出即为Wi-Fi 与约束后地磁的融合定位结果。

2.2 BP-AdaBoost-PSO 算法

BP-AdaBoost 算法能够有效提升定位精度，但迭代过程导致算法耗时相应增加。为了减少集成学习算法耗时，进一步利用PSO 对BP-AdaBoost 算法进行优化。

PSO 是一种通过搜索当前最优以获取全局最优的随机搜索算法[13]，优化后的BP-AdaBoost-PSO算法主要步骤如下。

步骤 1参数初始化

将PSO 的初始位置向量设为BP-AdaBoost 的权值与阈值，同时对PSO 中的有关参数进行初始设定。其中，将粒子维度设定为

式中：dinput和dhidden分别为输入层与隐含层神经元个数。

步骤 2更新粒子的速度与位置

对粒子的速度vh与位置ph进行更新，其表达式分别为

式中：h=1,2,···,Q，Q为粒子总数；f为惯性权重；c1和c2为 学 习 因 子；r1和r2为(0,1)之 间 的 随 机 数；pbesth为第h个粒子的个体极值；gbest为所有粒子的全局极值。

步骤 3更新个体与全局极值定义适应度函数fit 为

式中：Esum为测试集所有点的定位误差之和。

依据各粒子的适应度对个体和全局极值进行不断更新。当满足PSO 终止条件时，将最优个体作为权值和阈值赋给BP-AdaBoost。

3 粒子滤波融合

运动状态下利用BP-AdaBoost-PSO 进行连续定位时，仍可能存在由Wi-Fi 信号堆积导致的定位误差。针对这一问题，在本层融合定位方法中，利用PF 将PDR 定位结果与BP-AdaBoost-PSO 算法结果进一步融合。

PDR 通过智能便携设备中的惯性传感器信息实时解算出行人的步频、步长与航向[14]，再根据行人的上一位置推算出当前的位置信息，其定位原理如图3 所示。

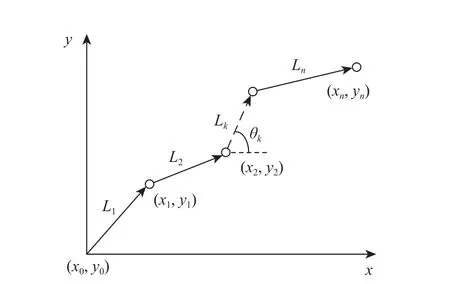
图3 PDR 定位原理Fig.3 Positioning principle of PDR

式中：Ln为 第n步的步长；θn为第n步的航向角。

采用文献[15]中的基于三重约束的波峰波谷检测计步模型，实现对步态的准确检测。步长估计采用Weinberg 在文献[16]中提出的经验模型：

式中：η为 常数；tk−1和tk分别为第k−1 步和第k步对应的时刻；amax(t)和amin(t)分别为间隔t内加速度的最大值和最小值。

利用陀螺仪积分计算航向时易产生误差累积，利用加速度计和磁力计计算航向时易受铁磁性物质干扰[17]。为了提高航向估计精度，采用互补滤波对上述2 种方式解算出的航向角进行融合。综合利用检测计步模型、步长估计和航向估计方法[15-17]解算出的步频、步长与航向信息，经推算可得PDR定位结果。

利用PF 将PDR 定位结果与BP-AdaBoost-PSO算法定位结果进行融合。将第α个粒子的初始坐标向量设定为

4 仿真结果与分析

基于分层优化的多源融合定位方法的总体框架如图4 所示。第1 层优化利用Wi-Fi 约束地磁匹配范围，第2 层优化利用PSO 降低BP-AdaBoost 算法耗时，第3 层优化利用PF 融合减少Wi-Fi 信号堆积。进一步利用真实定位场景中的实测数据对所提定位方法的定位性能进行仿真验证。

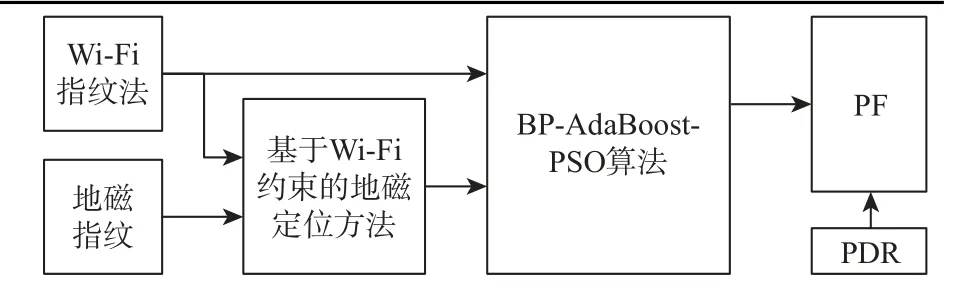
图4 融合定位方法框架Fig.4 Framework of fusion positioning algorithm

在北京航空航天大学新主楼内部选取2 个不同的定位场景。定位场景1 由封闭走廊和半露天走廊2 种环境特征构成，长30.0 m，宽15.6 m。定位场景2 长48.0 m，宽22.2 m，沿线途经走廊、大厅、天井等设施，环境特征较为丰富。在这2 个场景中分别选取原点O建立基准坐标系，如图5 和图6 所示。选用搭载自主开发APP 的小米6s 作为数据采集设备。Wi-Fi的采集频率设为10 Hz，加速度计、陀螺仪与磁力计的采集频率设为50 Hz。

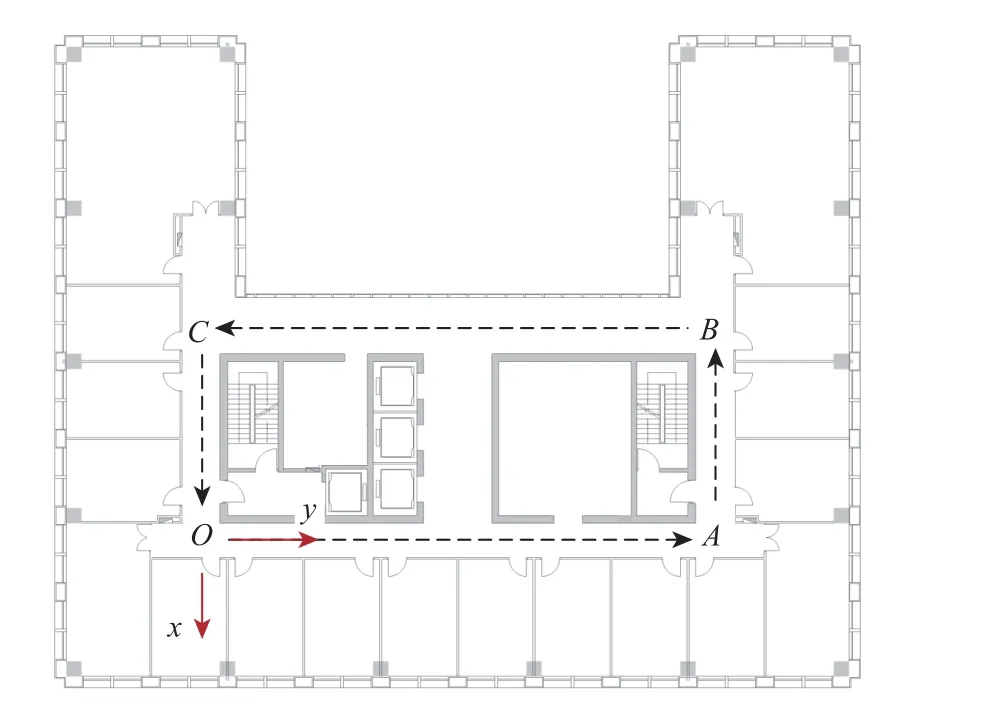
图5 定位场景1 平面图Fig.5 Plan of positioning site 1

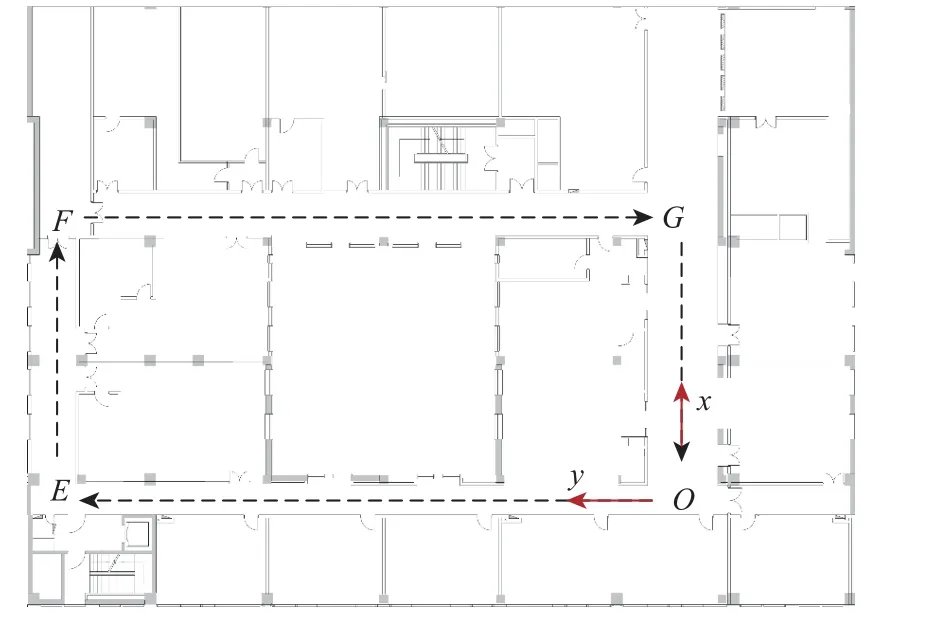
图6 定位场景2 平面图Fig.6 Plan of positioning site 2

离线阶段，将2 个定位场景划分为1.2 m × 1.2 m的网格，在各网格顶点采集Wi-Fi 信号强度和地磁强度数据，经预处理后建立指纹库。

在线阶段，分别采集行人静止和运动状态下在2 个场景中的实验数据。对于每个场景，在730 个真实坐标已知的待定位点采集行人静止状态下的数据，用于训练神经网络及获取Wi-Fi 的平均定位误差。行人运动状态下，为了便于对定位性能进行分析，沿预先设定的坐标已知的地标行走，每行走一步触发一次数据采集，沿O-A-B-C-O方向在定位场景1 中的不同路径重复行走100 圈，沿O-E-F-GO方向在定位场景2 中的不同路径重复行走100 圈。

4.1 地磁定位方法的定位性能

地磁定位方法的定位误差累积分布函数(cumulative distribution function, CDF)曲线如图7 所示。当CDF 为0.7 时，本文的约束方法和k-NN 算法的定位误差在场景1 中分别为2.06 m 和7.11 m，在场景2 中分别为2.03 m 和7.43 m。结果表明，基于Wi-Fi 约束的地磁定位方法能够有效降低行人运动状态下由地磁误匹配导致的定位误差。

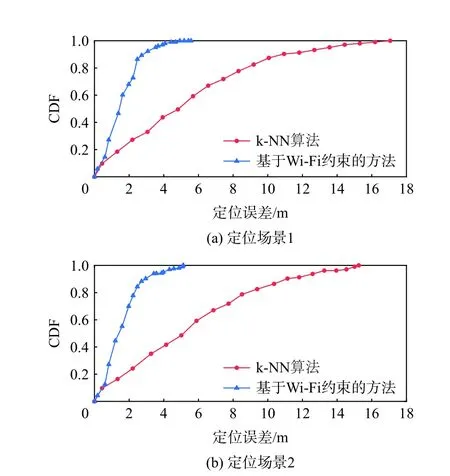
图7 不同地磁定位方法定位误差的CDF 曲线Fig.7 CDF curves of position errors with different geomagnetic positioning algorithm

对应的平均定位误差如表1 所示。可见，相较于k-NN 算法，基于Wi-Fi 约束的方法的平均定位误差在场景1 中降低了72.5%，在场景2 中降低了73.1%，定位精度得到了较大程度提升。

表1 不同地磁定位方法的平均定位误差Table 1 Average position errors of different geomagnetic positioning algorithms m

4.2 神经网络融合算法的定位性能

1）定位精度

图8 为神经网络融合算法的定位误差CDF 曲线。当CDF 为0.7 时，BP 算法、BP-AdaBoost 算法和BP-AdaBoost-PSO 算法的融合定位误差在场景1中 分 别 为1.25，1.18，1.17 m，在 场 景2 中 分 别 为1.27，1.16，1.16 m。结果表明，集成学习算法能够降低单一BP 易陷入局部最优导致的定位误差，提高Wi-Fi 与地磁的融合定位精度。而PSO优化前后的算法定位精度基本保持不变。

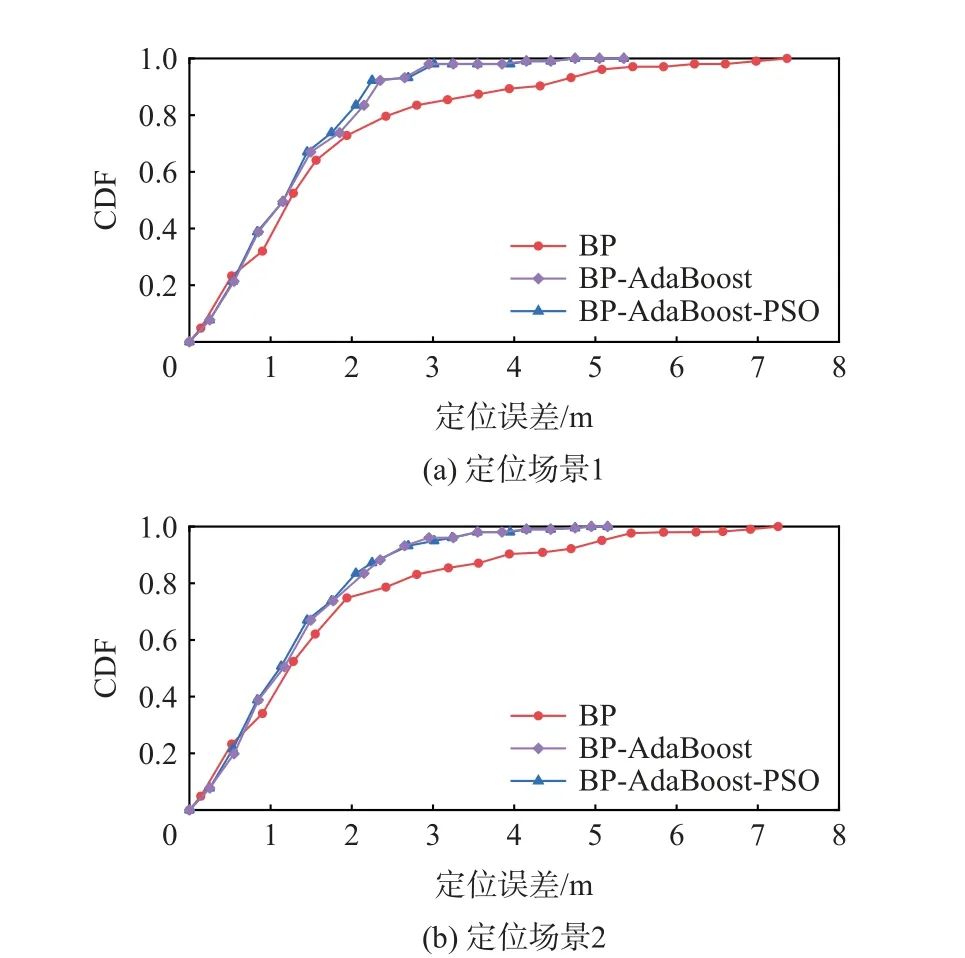
图8 神经网络融合算法定位误差的CDF 曲线Fig.8 CDF curves of position errors of neural network fusion algorithms

对应的平均定位误差如表2 所示。相较于BP，BP-AdaBoost 和BP-AdaBoost-PSO 的平均定位误差在定位场景1 中分别降低了6.5%和7.6%，在定位场景2 中分别降低了8.2%和9.3%，而BP-AdaBoost和BP-AdaBoost-PSO 两者的平均定位误差在2 个场景中均较为相近。

表2 神经网络融合算法的平均定位误差Table 2 Average position errors of neural network fusion algorithms m

2）算法耗时

以平均执行耗时作为评价指标，对神经网络融合算法耗时进行比较分析。

在2 个定位场景下，分别执行100 次融合算法并统计各自的平均执行耗时，如表3 所示。为了更加直观地显示耗时情况，分别在各场景下随机选取5 次统计结果，制成如图9 所示的柱状图。由于BP-AdaBoost 和BP-AdaBoost-PSO 存在迭代过程，在定位场景1 中，其平均执行耗时相较于BP 分别增加了49.4%和29.1%。但利用PSO 优化后的执行耗时较优化前减少了28.6%。在定位场景2 中，其平均执行耗时相较于BP 分别增加了49.8%和29.4%。但利用PSO 优化后的执行耗时较优化前减少了28.9%。结果表明，利用PSO 对BP-AdaBoost进行优化，能够降低平均执行耗时，加快算法收敛。

表3 平均执行耗时Table 3 Average execution time s

图9 执行耗时示意图Fig.9 Diagram of execution time

4.3 分层优化融合定位方法的定位性能

在2 个定位场景中，分别比较了PDR、BPAdaBoost-PSO 和分层优化融合定位方法的定位轨迹，如图10 所示，图中行人起始点的真实坐标分别为(0.9 m, 1.8 m)和(0.6 m, 0.6 m)。可 以 观 察 到，2 个定位场景下PDR 定位轨迹均在刚出发的6 m左右，与真实轨迹接近，随着时间推移，累积误差逐渐增大，行走结束时的坐标与真实起始点坐标存在较大偏离。

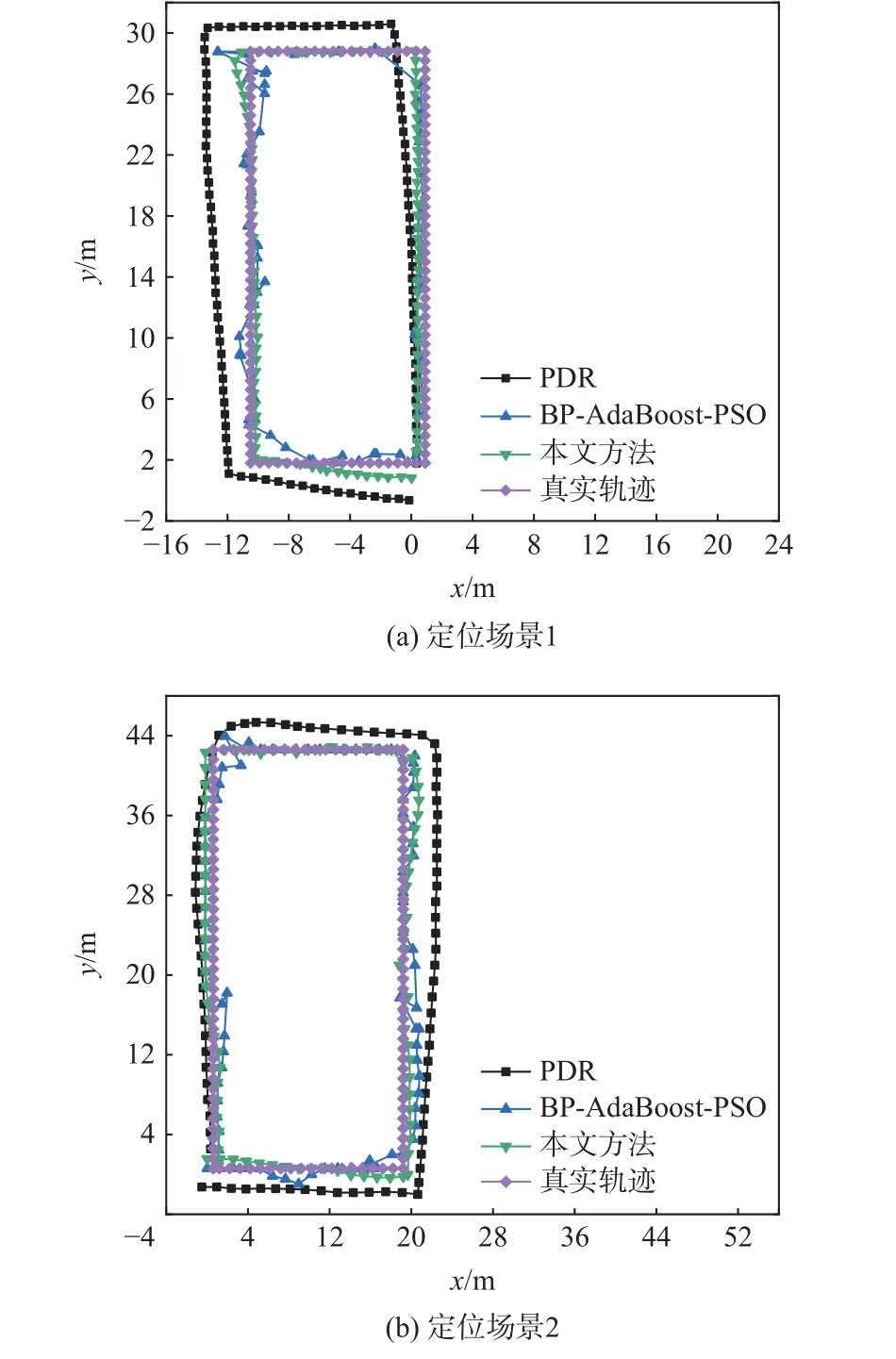
图10 定位轨迹对比Fig.10 Comparison of positioning trajectories

利用BP-AdaBoost-PSO 算法进行Wi-Fi/地磁融合定位时无误差累积，其定位轨迹与真实轨迹较为贴合，但由于Wi-Fi 信号堆积等原因，BP-AdaBoost-PSO 的部分Wi-Fi/地磁融合定位轨迹与真实轨迹仍存在一定程度偏离。利用PF 进一步融合PDR得到的定位轨迹与真实轨迹的偏离程度最小，定位精度得到了较大程度提升。

图11 为不同定位法对应的定位误差CDF 曲线。当CDF 为0.7 时，在定位场景1 中，PDR 和BPAdaBoost-PSO 融合定位误差分别为2.46 m 和1.17 m，分层优化融合定位方法为1.06 m。在定位场景2 中，PDR 和BP-AdaBoost-PSO 融合定位误差分别为2.52 m 和1.16 m，分层优化融合定位方法为1.03 m。结果表明，本文方法能够降低由于Wi-Fi 信号堆积导致的定位误差，同时降低PDR 误差累积的影响，提高行人运动状态下的连续定位精度，进一步提高系统整体定位性能。

图11 定位误差CDF 曲线对比Fig.11 Comparison of CDF curves of position errors

表4 为不同定位法的平均定位误差。相较于PDR 和BP-AdaBoost-PSO，本文方法的平均定位误差在定位场景1 中分别降低了50.4%和25.7%，在定位场景2 中分别降低了52.1%和24.7%，均具有更优的定位性能。

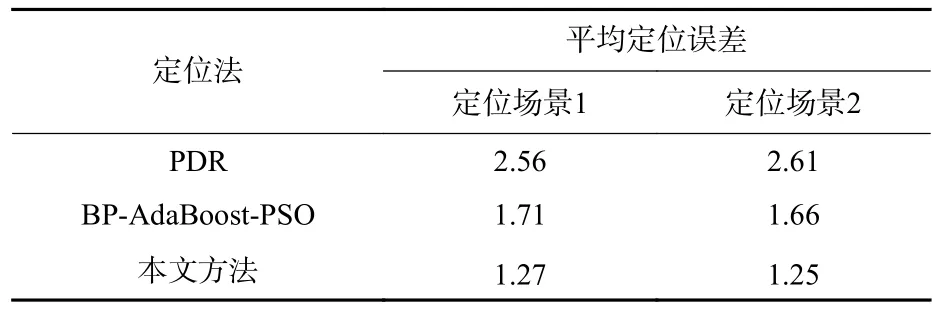
表4 融合定位的平均定位误差Table 4 Average position errors of fusion positioning algorithms m

5 结 论

1）基于Wi-Fi 约束的地磁定位算法的定位精度较传统k-NN 算法大幅提升。

2）优化后的BP-AdaBoost-PSO 算法能够在保证定位性能的同时，降低算法耗时。

3）不同场景下的定位性能仿真结果显示，本文方法能够较好解决行人运动状态下定位的连续性和稳定性问题。

本文方法有效降低了行人运动状态下由地磁误匹配、Wi-Fi 信号堆积和PDR 误差累积导致的定位误差，实现了在复杂室内环境下的精确连续定位，为解决行人室内定位问题提供了一种新的思路。