基于平流层飞艇的空基伪卫星路径规划算法

曲艺，王生，*，曾凌川，巩应奎

(1.中国科学院 空天信息创新研究院，北京 100094；2.中国科学院大学，北京 100049)

伪卫星是能够传播导航信号的发射器，最初布设于地面，用来验证卫星导航接收机[1]。随着技术的发展，伪卫星已成为改善卫星导航服务效能的重要手段之一，在组合导航、逆向导航、导航增强以及独立组网导航等方面取得了长足进展[2-9]。为扩大服务范围，增强部署灵活性，伪卫星依托的平台已从地基扩展到空基。在各类空基伪卫星平台中，平流层飞艇以其飞行动态性较小、覆盖面积大、驻空时间长等优势而备受青睐[10-15]。

鉴于基于平流层飞艇的空基伪卫星（以下简称“飞艇伪卫星”）的飞行高度远小于卫星轨道高度，其几何布局对于导航定位性能至关重要。文献[16]对2 种典型的浮空器导航定位系统方案进行了比较，指出对于同样数量的浮空器，因几何布局不同可导致导航定位精度相差1 个数量级。文献[17]对于空基伪卫星部署高度与覆盖范围之间的关系进行了计算，认为在4 颗空基伪卫星典型布局场景下，因伪卫星高度不同可导致服务区域面积相差数倍甚至数十倍。文献[11,14,18-19]针对精度、服务区域等不同的导航性能指标，以理论推导与经验相结合的方法提出了3 颗、4 颗、5 颗、6 颗空基伪卫星组网导航的几何布局方案。文献[18-24]则分别利用粒子群算法、遗传算法等现代启发式算法，设计了导航服务性能优化目标函数并对目标函数进行了全局寻优，获取了空基伪卫星组网导航的最佳布局方案。文献[15,22-24]讨论了地基伪卫星和空基伪卫星协同导航定位及性能增强问题，并采用多种方法，研究了地基伪卫星与空基伪卫星联合组网的几何配置问题。

以上研究均以经验方法或优化算法对飞艇伪卫星导航定位系统的几何布局进行了分析求解。然而大多聚焦于飞艇伪卫星几何布局的静态结果，却忽略了飞艇伪卫星构建几何布局的动态过程，特别是没有考虑飞艇伪卫星如何以最小的能源代价构建预期几何布局，也没有考虑飞艇伪卫星在构建预期几何布局过程中的伪卫星网络结构演变历程。

实际上，对于飞艇伪卫星来说，即使针对相同的初始位置和目标位置，不同飞行路径所需的能源总量差异很大，不同飞行路径导致的伪卫星网络结构演变历程差异也很大，且平流层飞艇属于低速飞行器，从起始位置飞行到目标位置需要较长时间，上述差异难以忽略。

综上所述，在飞艇伪卫星部署过程中，需要同时兼顾飞艇伪卫星的几何布局和飞行路径，使之能够以较低的能源代价获取较好的网络构型，进而提高导航服务的完好性、连续性与可用性。为此，本文首先梳理了飞艇伪卫星路径规划的性能指标，然后设计了具体的路径规划方法，对飞艇伪卫星从起始位置到目标位置运行路径的网络构型与能源消耗进行全程分析评价，最后对该方法进行了仿真分析，验证了方法的有效性，并对多种输入条件下的仿真结果进行了初步分析。

1 飞艇伪卫星路径规划性能指标

1.1 几何构型指标

设(xj，yj，zj)是第j颗伪卫星的位置，c为光速，用户的位置和接收机钟差分别为(xu，yu，zu)和tu，则用户接收机测量到的第j颗伪卫星到用户的伪距观测值为

将式(1)进行一阶泰勒展开，可以得到

式中：(Δxu，Δyu，Δzu)为用户的真实位置与近似位置之差；(axj，ayj，azj)为用户近似位置到第j颗伪卫星的方向余弦。

若不考虑导航电文中的星历数据误差和卫星相位误差，且假设参与定位的伪卫星数量为n，则式(2)可扩展为

其中：矩阵H的元素分别为

对于式(3)，应用最小二乘法可得

若各伪距测量噪声线性无关，方差为σ2，则Δx的协方差为

由式（7）可知，(HTH)−1反映了伪距测量误差与定位误差之间关系，其迹的平方根通常被定义为几何精度因子（geometric dilution of precision，GDOP），用以反映伪距测量误差到定位误差的放大倍数[25]，即

伪卫星为某点提供定位服务的性能可用该点的GDOP 数值评价，而伪卫星为某个区域提供定位服务的性能，多以区域内采样点的GDOP 数值分布图或GDOP 等值线图来表示[13,15,19,26]。具体到量化评价方法，第1 类是采用伪卫星覆盖范围内均匀分布采样点的GDOP 均值进行评价[20,27-29]，如式(9)所示；第2 类是以GDOP 数值小于某阈值的采样点占全部采样点的百分比进行评价[19,30]。由于第2 类量化评价方法的阈值选取具有主观性，因此，本文以第1 类量化方法评价飞艇伪卫星为某个区域提供定位服务的性能，即

式中：b1为服务区域内均匀分布的采样点数量；GDOPi为服务区域内第i个采样点的GDOP 数值；GDOP为服务区域内全部采样点的GDOP 平均值，后文以 GDOP作为飞艇伪卫星路径规划代价函数中的定位服务性能指标。

进而，由于飞艇伪卫星处于位置j时，服务区内定位性能可用 GDOPj表示，则飞艇伪卫星从起始位置到目标位置的飞行过程的导航服务性能可以用飞艇伪卫星处于飞行路径全部节点的 GDOP平均值（以下简称“路径GDOP 均值”）评价，即

式中：b2为飞艇伪卫星飞行路径的节点数量；GDOPj为飞艇伪卫星处于飞行路径节点j时服务区域内全部采样点的GDOP 平均值，后文以 GDOP 作为飞艇伪卫星路径规划结果的导航服务性能评价指标。

1.2 能源消耗指标

飞艇伪卫星依托的平台—平流层飞艇作为一种浮空器，在能源消耗方面与无人机、导弹等飞行器存在显著差异。平流层飞艇主要依靠净浮力升空、驻空，通过螺旋桨推力实现工作高度的位置保持与巡航飞行。因此，平流层飞艇在飞行过程中的能源消耗不仅取决于动力学作用，还取决于大气、风场等环境因素[31-35]。

本文研究的重点在于飞艇伪卫星的飞行路径优化策略，因此，将平流层飞艇简化为质点模型，并做如下假设：平流层飞艇的浮力与重力相等，即平流层飞艇的高度调节无需消耗能源；平流层飞艇的迎角、侧滑角和滚转角为0；平流层飞艇飞行过程中自身质量不变。

1.2.1 平流层飞艇动力学模型

平流层飞艇的动力学方程为

式中：mtotal为平流层飞艇质量m与平流层飞艇附加质量madd之和；U为平流层飞艇飞行的空速；T为螺旋桨产生的推力；D为气动阻力。

mtotal的计算公式为

式中：k1、k2、k3为平流层飞艇在各个方向的附加质量系数；ρair(h)为高度h处的大气密度；V为平流层飞艇体积；m为平流层飞艇质量，max、may、maz分别为平流层飞艇在x方向、y方向、z方向的附加质量。

气动阻力D的计算公式为

式中：Sref为平流层飞艇参考面积；CD为平流层飞艇的气动系数，可以利用其长细比计算[36]。

对于平流层飞艇，参考面积Sref通常用式（14）表示：

1.2.2 风场模型

风场随经纬度、高度、季节、时间等发生显著变化。大体而言，风速在对流层随高度增加而增加，到约10～15 km 处达到极值，而后又逐渐下降，到平流层底部的准零风层降至低点[31-32,37]。

为了降低计算量，本文暂不考虑风场随季节、时间的变化，采用简化的七阶多项式拟合指定区域各个高度的水平风场，并以北半球某地秋季风场数据为例拟合其系数[38]，即风场模型的表达式为

式中：We为风速东向分量；Wn为风速北向分量；h′为标准化高度，计算公式为

其中：h为平流层飞艇距海平面的高度。

拟合出的该地风速东向分量系数和风速北向分量系数分别为[38]

1.2.3 平流层飞艇能源消耗模型

平流层飞艇飞行所消耗的能量主要包括推进螺旋桨消耗的能量和舵面消耗的能量，即

式中：Jp、Jδr分别为推进螺旋桨、舵面消耗的能量。

推进螺旋桨消耗的功率按匀速平飞工况核算，此时推进螺旋桨产生的推力与阻力大小相等，方向相反，即在空速U下产生推力T所需能耗功率为[39]

式中：ηp和ηe分别为推进效率和电机效率，根据文献[33]，ηe与ηp均可假设为常数。

若平流层飞艇飞行时长为t，则在此期间推进螺旋桨的能源消耗可以表示为

其中：cδr为方向舵铰链力矩系数；q∞为平流层飞艇动压；Lref为平流层飞艇参考长度；δr为方向舵偏角。

平流层飞艇动压q∞的计算公式为

式中：U为平流层飞艇飞行的空速。

平流层飞艇参考长度Lref的计算公式为

为了简化问题，假设舵面匀速转动，则方向舵舵面消耗的能源可表示为[40]

由式(24)可知，当方向舵偏角 δr= 0，即平流层飞艇不转弯时，Jδr= 0，平流层飞艇消耗的能量J等于推进螺旋桨消耗的能量Jp。后文以J作为飞艇伪卫星能源消耗的评价指标。

2 飞艇伪卫星路径规划算法

2.1 规划空间建立与路径表示

为了高效直观地表达飞艇伪卫星的飞行路径，本文采用栅格法描述规划空间，将实际的物理空间映射为虚拟的算法网格，即在地固坐标系下将规划空间栅格化为立体网格，然后判断网格节点之间的连通性，计算飞艇伪卫星在网格节点之间飞行所需的代价，从路径规划起点开始，依次向代价最小的可连通节点移动，直至路径规划终点，以所经过节点的连线表示飞艇伪卫星的飞行路径。

假设飞艇伪卫星规划空间的经度范围、纬度范围、高度范围分别为[lw,le]、[ss,sb]、[el,eh]，算法网格在经度方向、纬度方向、高度方向分别栅格化为nl、ns、ne个节点，则对于算法网格中的任一节点N(ni,nj,nk)，对应的规划空间经度lN、纬度sN、高度eN分别为

节点N(ni,nj,nk)在算法网格内的可连通节点集合为：Q={(qi,qj,qk),qi=ni±1,qj=nj±1,qk=nk±1,(ni−1 ≥1)&&(ni+1 ≤nl), (nj−1 ≥1)&&(nj+1 ≤ns),(nk−1 ≥1)&&(nk+1 ≤ne)}。具体规划时，可以通过调整规划空间的栅格数量实现计算量与路径规划精度需求的平衡。

2.2 代价函数

为了综合考虑第1 节定义的2 项指标，本文将路径规划代价函数定义为

式中：WG为代价函数中GDOP 均值变化量所占权重；WJ为代价函数中飞艇伪卫星能源消耗所占权重；GDOPA、GDOPE分 别 表 示 飞 艇 伪 卫 星 处 于A点、路径规划终点时服务区域内全部采样点的GDOP 均值；JAB为飞艇伪卫星从A点飞行到B点的能源消耗。

即算法网格中不可连通节点间的代价为无穷大，而可连通节点间的代价包括2 部分：①飞艇伪卫星服务区域内全部采样点的GDOP 均值变化量；②飞艇伪卫星能源消耗。由于GDOP 均值变化量与飞艇伪卫星能源消耗属于不同类型的物理量，不宜直接叠加，因此，本文将其分别归一化后再相加。假设飞艇伪卫星处于路径规划起点时服务区域内全部采样点的GDOP均值为 GDOPS，飞艇伪卫星到达路径规划终点后服务区域内全部采样点的GDOP 均值为 GDOPE，飞艇伪卫星从路径规划起点沿直线飞行到路径规划终点的能源消耗为JSE，则物理量归一化后的路径规划代价函数演变为

对于代价函数中的权重，有

WG与WJ此消彼长，决定了在路径规划中优先考虑飞艇伪卫星能源消耗还是优先考虑GDOP 均值变化量。若优先考虑飞艇伪卫星能源消耗，则服务区域的GDOP 改善程度可能会有所减缓；反之则可能增加飞艇伪卫星的能源消耗。

2.3 约束条件

一般飞行器路径规划考虑的约束主要包括最小航迹段长度、最大转弯角、最大节点数量、最大爬升角/俯冲角、最低飞行高度限制等[41]。

由于平流层飞艇属于低速飞行器，可以实现大角度转弯甚至悬停，因此最小航迹段长度、最大转弯角、最大节点数量等限制对平流层飞艇可以暂不考虑[39]。对于最大爬升角/俯冲角，本文通过规划空间网格划分数量加以调节。对于最低飞行高度，本文通过规划空间高度范围加以限制。

2.4 路径搜索算法

在明确了算法网格与代价函数后，本文将飞艇伪卫星路径规划问题转化为算法网格内的最短路径搜索问题。可将算法网格视为有向赋权图，网格节点视为图顶点，网格节点之间的代价视为边的权值，则飞艇伪卫星路径规划可视为寻求图中从规划起点到规划终点的代价最低的路径。

最短路径搜索问题的经典求解方法包括floyd算法、dijkstra 算法、A*算法等。floyd 算法属于遍历求解，主要解决多源最短路径问题，计算量大，运行速度较低；dijkstra 算法采用贪心算法策略，可解决单源最短路径问题，同样存在遍历节点多、内存占用量大等缺陷，难以用于大型路径规划中；A*算法属于启发式算法，在扩展搜索节点时选择代价最小的节点加以扩展，具有搜索节点数量少、搜索效率高、鲁棒性好等优点[42-44]。综上，考虑到飞艇伪卫星路径规划问题规模较大，且路径前后节点的代价存在关联，本文选择A*算法开展研究。

A*算法的代价函数定义为

式中：f(x)为综合代价函数；g(x)为实际代价函数；h(x)为启发代价函数，也是预计代价函数。

本文对上述2 个函数的定义均如式(27)所示，只是g(x)中GDOP 代价与能耗代价均是从当前点到扩展点的实际代价，而h(x)中GDOP 代价与能耗代价均是从扩展点到路径规划终点的预期代价。

A*算法维护CLOSE 和OPEN 这2 个表，前者保存算法网格中已得到从起始节点到当前节点最短路径的节点，后者保存算法网格中的可扩展节点，算法基本的搜索步骤如下：

步骤 1初始时，将路径规划起始节点s放入OPEN 表。

步骤 2对OPEN 表中各个节点的综合代价函数从小到大进行排序。

步骤 3计算OPEN 表中综合代价函数最低者进行扩展，将扩展节点放入OPEN 表。

步骤 4将OPEN 表中第一个节点移至CLOSE 表。

步骤 5重复步骤2～步骤4，直到OPEN 表中没有节点或找到路径规划终点。

3 仿真分析

本文以1 颗飞艇伪卫星和多颗地基伪卫星协同定位为背景进行飞艇伪卫星路径规划仿真，多颗飞艇伪卫星组网定位的路径规划仿真可在此基础上略加改动获得。

在飞艇伪卫星与地基伪卫星协同定位场景下，飞艇伪卫星路径规划受飞艇伪卫星飞行速度、路径规划起始位置、规划空间网格划分数量等多种条件影响，本文算法对上述输入条件不加以限制，后文所列仿真结果仅是一种或几种条件下的仿真结果，用以验证算法。仿真工具采用MATLAB 2015b。

3.1 仿真流程

本文仿真的主要流程如图1 所示。

图1 仿真流程Fig.1 Flow chart of simulation

3.2 仿真参数设置

1 ) 大气模型采用美国标准大气模型[45]。

2 ) 导航服务区域经度范围：107°E～109°E。

3 ) 导航服务区域纬度范围：39°N～41°N。

4 ) 导航服务区域经度方向、纬度方向采样点数量：20×20。

5 ) 规划空间高度范围：2～22 km。

6 ) 平流层飞艇体积：30 000 m3。

7 ) 平流层飞艇轴向气动系数0.025，法向气动系数0.18，电机效率0.7，推进效率0.9，铰链力矩系数2.8× 10−4。

8 ) 平流层飞艇飞行速度（除3.3.2 节外）：30 m/s。

9 ) 路 径 规 划 起 始 位 置（除3.3.3 节 外）：经 度108.8°E，纬度39.2°N，高度2 km。

10 ) 规划空间经度、纬度、高度方向网格划分数量（除3.3.4 节外）：20×2 0× 10。

11 ) 参与组网的地基伪卫星位置：

地基伪卫星1(107°E,39°N,1 km)；

地基伪卫星2(107°E,41°N,2 km）；

地基伪卫星3(109°E,41°N,3 km)；

地基伪卫星4(109°E,39°N,4 km)。

3.3 仿真结果

本节首先对飞艇伪卫星路径规划结果与直线飞行路径（未经规划的路径）进行比较，然后对多种仿真条件下的路径规划结果进行对比分析。

除3.3.1 节外，后文的性能比较分析均采用GDOP 均值变化量与飞艇伪卫星能源消耗平均权重（即式(27)中WG=WJ=1/2）的路径规划结果。

3.3.1 路径规划结果与直线飞行路径性能比较

本文在3 种权重设置下进行了路径规划，3 种不同的权重设计分别为

1 ) GDOP 均值变化量权重优先，飞艇伪卫星能源消耗权重为0，即式(27)中，WG=1，WJ=0。

2 ) 飞艇伪卫星能源消耗权重优先，GDOP 均值变化量权重为0，即式(27)中，WG=0，WJ=1。

3 ) GDOP 均值变化量与飞艇伪卫星能源消耗权重相等均为1/2，即式(27)中，WG=1/2，WJ=1/2。

3 种权重下的路径规划结果及其性能比较如图2 所示。可以看到，权重设置对路径规划结果影响较大。GDOP 均值变化量权重优先的情况下，伪卫星网络GDOP 收敛较快，但是其能源消耗最大；反之，飞艇伪卫星能源消耗权重优先的情况下，飞艇伪卫星能源消耗最少，但是其网络GDOP 收敛较慢；GDOP 均值变化量与飞艇伪卫星能源消耗平均权重情况下，伪卫星网络GDOP 与能源消耗适中。

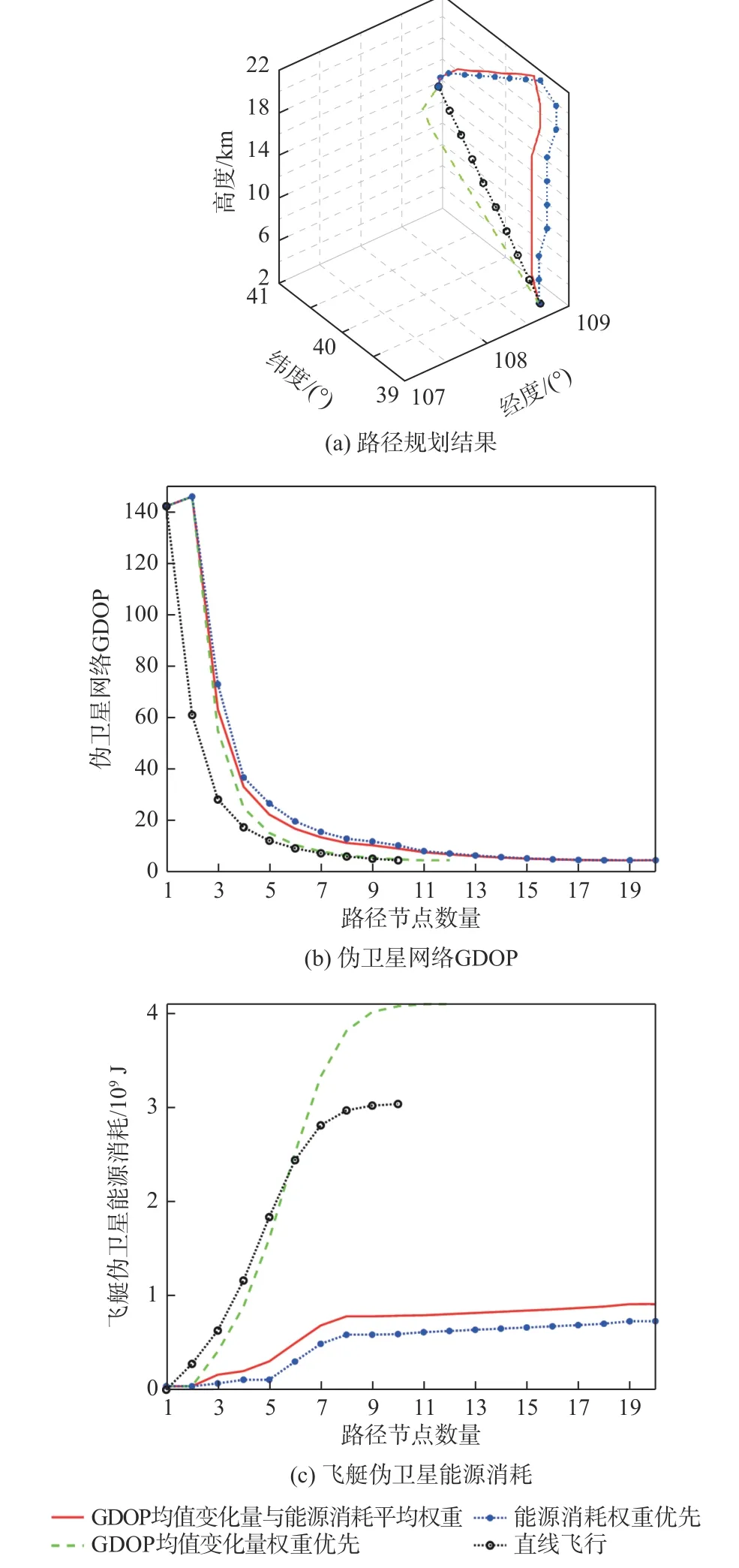
图2 路径规划结果与直线飞行路径的对比Fig.2 Comparison among path planning results and rectilinear flight path

表1 为路径规划结果与直线飞行路径性能比较情况。可以看出，与直线飞行路径相比，路径规划结果可以有效改善飞艇伪卫星性能。在GDOP均值变化量与飞艇伪卫星能源消耗平均权重的情况下，路径GDOP 均值降幅可达31.50%，能源消耗降幅可达70.03%。3 种权重下，平流层飞艇方向舵消耗的能源分别为7.04×104J、0.30×104J、1.40×105J，与路径中的转弯数量与转弯角度相关，但总体来说，方向舵能耗在总体能耗中占比很小。

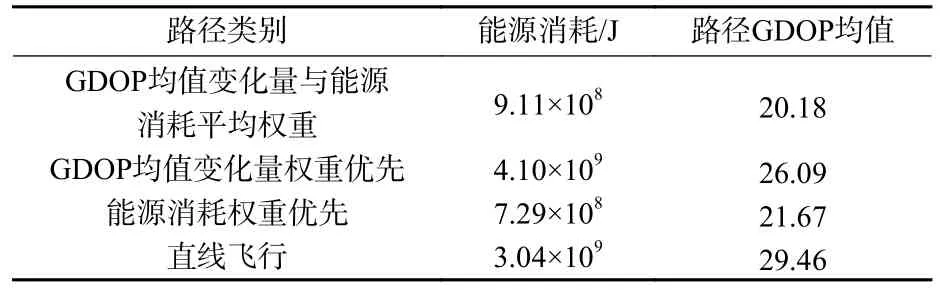
表1 路径规划结果与直线飞行路径性能比较Table 1 Performance comparison among path planning results and rectilinear flight path

3.3.2 飞行速度对路径规划的影响

为研究飞艇伪卫星飞行速度对于路径规划结果的影响，本文在其他仿真参数均与3.2 节一致的条件下，选择4 种飞艇伪卫星飞行速度20 m/s、25 m/s、30 m/s 和35 m/s 进行仿真，仿真结果如图3 所示。4 种飞行速度下，飞艇伪卫星的能源消耗与路径GDOP 均值如表2 所示。

表2 不同飞行速度的路径规划结果性能比较Table 2 Performance comparison among path planning results of different flight speeds

图3 不同飞行速度的路径规划结果对比Fig.3 Comparison among path planning results of different flight speeds

从图3 和表2 来看，对于本文设置的仿真条件，飞艇伪卫星在20 m/s、25 m/s 速度下的路径规划结果接近，在30 m/s、35 m/s 速度下的路径规划结果接近，4 种路径规划结果的GDOP 均值相差不大，但是飞艇伪卫星能源消耗存在约26%的差异。

3.3.3 规划起点对路径规划的影响

为比较路径规划起点对于飞艇伪卫星路径规划结果的影响，本文在其他仿真参数均与3.2 节一致的条件下，选择5 种规划起点对于飞艇伪卫星路径进行规划，5 种不同的规划起点分别为服务区域的4 个边界点和服务区域的中心点，仿真结果如图4所示。5 种规划起点下，飞艇伪卫星的能源消耗与路径GDOP 均值如表3 所示。

表3 不同规划起点的路径规划结果性能比较Table 3 Performance comparison among path planning results of different planning starting points

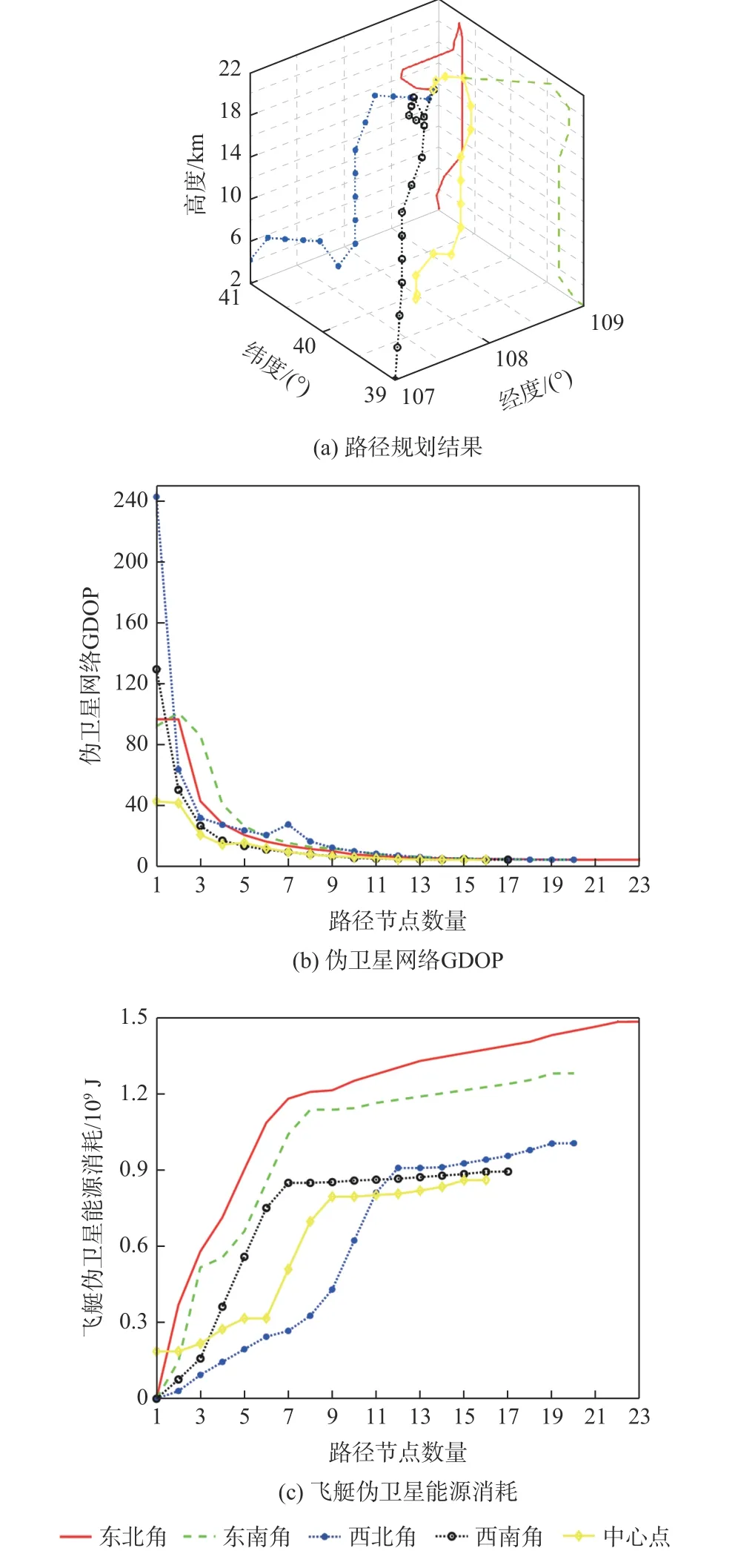
图4 不同规划起点的路径规划结果对比Fig.4 Comparison among path planning results of different planning starting points

从图4 和表3 来看，对于本文设置的仿真条件，以服务区域中心作为飞艇伪卫星路径规划的起点最为有利，伪卫星网络GDOP 改善效果最为明显，路径GDOP 均值较表中最大值减少51.08%，且飞艇伪卫星能源消耗最少，能源消耗较表中最大值减少41.82%。其他起点的路径规划结果则在伪卫星网络GDOP、飞艇伪卫星能源消耗等方面表现不一。

3.3.4 规划空间网格划分数量对路径规划的影响

为分析规划空间网格划分数量对飞艇伪卫星路径规划结果的影响，本文在其他仿真参数均与3.2 节一致的条件下，分别在水平方向、垂直方向对规划空间进行了多种网格划分。首先，将垂直方向网格数量固定为10，水平方向网格划分数量分别为10×10、15×15、20×20、25×25、30×30、35×35、40×40，其路径规划结果、飞艇伪卫星的能源消耗与路径GDOP 均值如图5 和表4 所示。然后，将水平方向网格数量固定为15×15，垂直方向网格划分数量分别为10、15、20、25、30、35、40，其路径规划结果，飞艇伪卫星的能源消耗与路径GDOP 均值如图6和表5 所示。

表4 不同水平方向网格数量的路径规划结果性能比较Table 4 Performance comparison among path planning results with different numbers of grids in horizontal direction

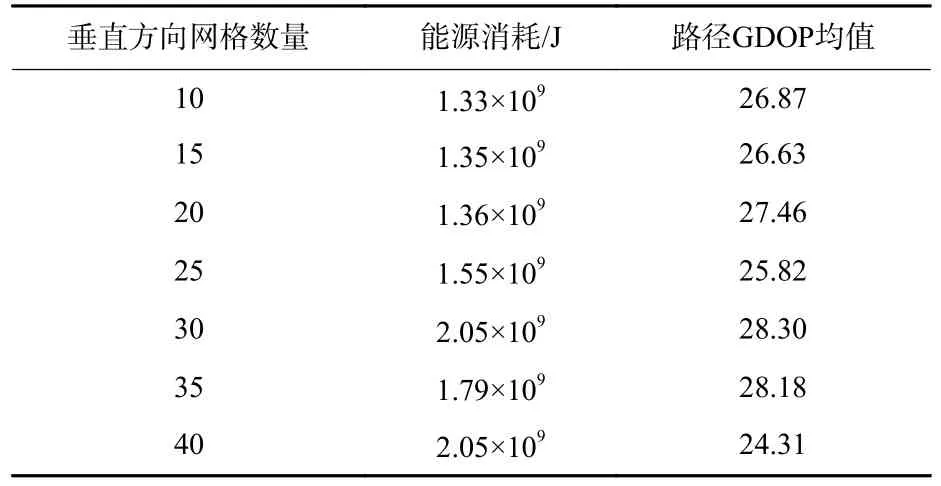
表5 不同垂直方向网格数量的路径规划结果性能比较Table 5 Performance comparison among path planning results with different numbers of grids in vertical direction

图5 不同水平方向网格数量的路径规划结果对比Fig.5 Comparison among path planning results of different numbers of grids in horizontal direction

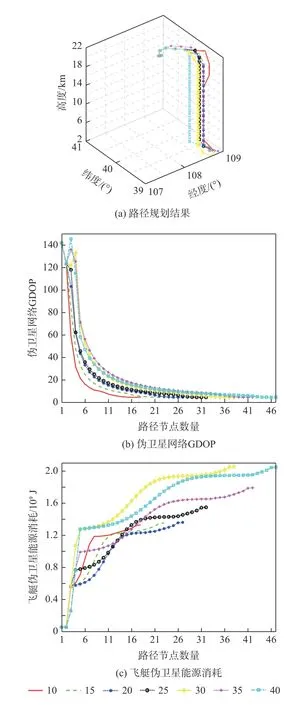
图6 不同垂直方向网格数量的路径规划结果对比Fig.6 Comparison among path planning results of different numbers of grids in vertical direction

从仿真结果来看，在本文设置的仿真条件下，水平方向网格划分数量从10×10 增加到40×40，路径GDOP 均值与飞艇伪卫星能源消耗总体呈改善趋势，路径GDOP 均值降幅达39.92%，飞艇伪卫星能源消耗降幅达35.18%。而垂直方向网格划分数量从10 增加到40，飞艇伪卫星性能没有得到大幅改善。

4 结 论

1）在飞艇伪卫星导航服务应用需求日益迫切的背景下，有必要开展飞艇伪卫星路径规划研究，以便用最低的能源代价获取最优的导航服务效果。

2）本文的飞艇伪卫星路径规划方法能够在改善伪卫星网络GDOP 的同时，大幅降低飞艇伪卫星能源消耗。在本文的仿真条件下，路径规划结果与直线飞行路径相比，路径GDOP 均值与飞艇伪卫星能源消耗的降幅均超30%。

3）飞艇伪卫星路径规划结果受多种因素影响。从仿真结果来看，飞艇伪卫星飞行速度从20 m/s增加到35 m/s，路径GDOP 均值变化不明显，但是能源消耗差异较大；与服务区域边界点作为飞艇伪卫星路径规划起点相比，将服务区域中心点作为飞艇伪卫星路径规划起点在路径GDOP 均值、能源消耗等方面存在明显优势；在水平方向增加规划空间网格划分数量，有助于改善路径GDOP均值，降低飞艇伪卫星能源消耗。

4）本文对所用风场模型、飞艇动力学模型等均进行了简化假设，实际风场中包含定常风、风切变、大气紊流、突风等多种复杂因素，飞艇伪卫星飞行过程中也可能发生变速运动、飞艇质量变化等情况，后续可对此进行更为详尽的分析研究。