基于时空图卷积神经网络的离港航班延误预测

姜雨，陈名扬，袁琪，戴垚宇

(南京航空航天大学 民航学院，南京 211106)

随着民航运输需求量的不断提升，航班延误问题已经成为限制民用机场发展的主要瓶颈之一。同时伴随机场网络的规模持续扩张，机场之间的航班延误传播现象愈发频繁[1]。因此，如何精准高效地预测航班延误就变得至关重要，这不仅可以提前感知机场航班延误发生的可能性[2-3]，还能够反映航班延误的波动情况[4]。

纵观国内外学者的相关研究，对航班延误预测问题大多采用构建预测模型的解决方式，并且研究对象主要集中在航班延误波及、航线延误和机场航班延误。Cai[5]和Hao[6]等构建航班延迟模型以分析延误波及问题；Guo[7]、Thiagarajan[8]和罗谦[9]等从航线延误角度出发构建航班延误预测模型；王春政等[10]致力于研究机场网络中各子系统间的延误特征并提出基于Agent 的机场网络延误预测模型；Khanmohammadi 等[11]基于自适应网络构建了模糊推理系统和模糊决策系统，可分别执行航班延误预测和飞机降落计划制定两大任务。

近些年来，随着人工智能的迅速发展，越来越多的学者运用深度学习的思想去解决交通运输领域的预测问题[12-13]，常见的深度学习算法有卷积神经网络（convolutional neural networks, CNN）和循环神经网络（recurrent neural network, RNN）等。吴仁彪等[14]在CNN 的基础上增设直通通道并引入卷积衰减因子以控制不同深度网络的特征叠加比例，从而维持航班延误预测模型的稳定性。部分学者提出 使 用 图 卷 积 神 经 网 络[15-18]（graph convolutional network, GCN）捕捉交通网络中的空间特征以提升预测精度。Yin[19]和冯宁[20]等利用谱图卷积方法将卷积操作应用至图结构数据以提取路网中的空间特征，从结果来看这种方法使得预测模型具有相对较高的预测精度和稳定性，因此，如何将GCN 引入机场网络中进行航班延误预测亟待研究。

本文从航班延误预测的时间序列特性出发构建机场网络，在GCN 的基础上建立基于时空图卷积神经网络（spatio-temporal graph convolutional networks,STGCN）的离港航班延误预测模型，并使用TensorFlow为深度学习框架进行模型训练和实例分析。

1 机场网络与谱图卷积

1.1 机场网络模型设计

本文对航班延误预测问题的表达式为

式中：vt∈Rn为第t时间段的n个机场的观测向量，向量中每个元素都代表了对应机场的观测值。式(1)表 示 由 前m个 延 误 观 测 值vt−m+1,vt−m+2,···,vt，去预测下一个步长为h的时间段内的延误预测值vˆt+1,vˆt+2,···,vˆt+h。

综上定义第t时间段的机场网络图结构为图Gt=(Vt,E,W)。其中，Vt为节点集，对应于各机场的延误值；E为边的集合，表示各机场之间的连接性，每个机场的观测值并不是互相独立而是成对连接的；W为Gt的 加权邻接矩阵，其元素wij为 节点i和j之间的权重，同时也表征了对应2 座机场之间的连接度，这种连接度能够反映出机场间的空间关联性。不同时间段的机场网络按时间序列进行排列，使得每个机场网络图中的延误状态信息是一种按照时序动态变化的图信号，最终形成机场网络图结构的网络数据，具体如图1 所示。

图1 机场网络图结构的网络数据Fig.1 Network data of airport network graph structure

机场网络的加权邻接矩阵W反映了机场间的空间关联性。W可根据各机场之间的周航班频次计算得出，其元素具体公式为

式中：wij为 机场i和 机场j之间边的权重；fij为机场i和 机场j之间的周航班频次；fmax和fmin分别为最大航班频次和最小航班频次；ε为控制邻接矩阵分布和稀疏性的阈值，取 ε =0.2。

1.2 基于谱的图卷积方法

GCN 是一种研究图的神经网络，其本质在于提取网络中的空间特征。目前图卷积方法大致有2类：一种是基于空间域的图卷积；另一种是基于谱的图卷积。1.1 节所提出的机场网络图结构属于拓扑图，其包含了节点自身的节点特征和各节点之间的结构特征，并且拥有关于图的邻接矩阵，这使得机场网络满足谱图的生成条件，因此，采用基于谱的图卷积方法研究机场网络的空间特征。

谱图卷积的主要思想是利用傅里叶变化将图信号从空间域转换为谱域，之后再进行卷积运算。谱图卷积相关公式为

式中：L∈Rn×n为 图的拉普拉斯矩阵；I∈Rn×n为单位矩阵；D∈Rn×n为对角度矩阵，其对角线上的元素是各 节 点 的 度 数；U∈Rn×n为L的 特 征 向 量 矩 阵；Λ=diag([λ0,λ1,···,λn−1])∈Rn×n为对角阵，λi为L的特征值；X∈Rn×n为输入的图信号；“∗g”表示图卷积运算；Θ (Λ)为一个滤波器，是一个对角矩阵。

式(3)表示拉普拉斯矩阵L的谱分解，式(4)表示图信号X通过核 Θ 与 傅里叶变化UTX相乘，完成由不规则的图结构数据转换为规则结构数据的过程，以便之后进行卷积操作，最终完成各节点特征和结构特征的信息聚合。

2 航班延误预测模型构建

2.1 STGCN 结构构建

从机场网络的整体性出发捕捉航班延误的时间特征和空间特征，并且在时间轴上采用完全卷积结构。基于此，将STGCN 用于预测航班延误。STGCN的结构如图2 所示，其中同一模块使用相同颜色表示。

图2 STGCN 结构Fig.2 Architecture of STGCN

STGCN 主体由时空卷积块和输出层构成，图2右侧部分反映了模型的整体流程，输入是已知前m个时间段的延误观测值vt−m+1,vt−m+2,···,vt，通过时空卷积块提取输入值的时间特征和空间特征，并在输出层进行特征整合，最终输出延误预测值vˆ。

2.2 提取空间特征的空间图卷积

为考虑到机场网络的连通性和全局性，将图卷积直接运用至图结构数据以提取网络的空间特征。在式(4)所对应的谱图卷积中，网络的复杂度为O(n2)，因此，使用切比雪夫多项式作为近似策略进行逼近以降低复杂度。

定义卷积核为对角阵 Λ的多项式，记作

式中：θ ∈RK为多项式系数的向量；K为图卷积核的大小。

切比雪夫多项式Tk(x)用 来近似滤波器为K−1阶的截断展开式，即

基于此对图卷积式(4)进行重新定义，具体为

式中：Tk为缩放后的拉普拉斯矩阵L˜ 的k阶切比雪夫多项式。使用切比雪夫多项式进行逼近后计算局部卷积，网络的学习复杂度降为O(K|E|)。

2.3 提取时间特征的时间门控卷积

由于CNN 具有训练速度快、结构简单等特点，因此，采用卷积结构捕捉机场网络中发生航班延误时的时间特征。如图2 左侧所示，时间门控卷积层中设有一个一维因果卷积，其卷积核大小为KT，而后连接一个门控线性单元（gated linear units, GLU）激活。对于机场网络中的各节点，时间门控卷积对输入元素的KT个近邻进行挖掘，使得序列长度逐次缩短KT−1。基于此，对每个节点的输入视为一个长度为M、通道数为Ci的时间序列，因此将输入设为Y∈RM×Ci。时间门控卷积的定义为

式中：Γ ∈RKT×Ci×2Co为时间门控卷积核，Co为输出特征的通道数；“∗Υ”表示卷积操作；P和Q为GLU 的输入；“⊙”表示哈达玛乘法。式(10)是指将输入Y通过卷积核 Γ映射到单一输出元素R(M−KT+1)×(2Co)，且P和Q的 通 道 数 相 同。Sigmoid 门σ(Q)的作用是控制哪些输入信息可以传入下一层。使用GLU 不仅能通过堆叠卷积层从而充分利用输入，还能在各卷积层间形成残差连接以防止梯度消失。

2.4 时空卷积块

时空卷积块的主要结构如图2 中间所示，其中空间图卷积负责提取图中的空间特征，时间门控卷积则用于提取时间特征。利用空间图卷积连接2 个门控卷积，可以完成由网络卷积向时序卷积的快速空间状态传播。此外时空卷积块中采用层标准化以防止模型过拟合。

设时空卷积块l的输入为vl∈RM×n×Cl，输出为vl+1 ∈R(M−2(KT−1))×n×Cl+1，且它们都是三维张量，具体计算公式为

图2 右侧部分中的输出层由一个时间门控卷积与全连接层组成，门控卷积将时空卷积块的输出映射为单步预测，之后获得中间输出结果Z∈Rn×c，并通过式(12)得到延误预测值vˆ为

式中：a∈Rc为待训练的权重；b为偏置项。

最后运用 L2损 失函数衡量预测值vˆ与真实值v的不一致程度，具体公式为

式 中：A为 可 训 练 的 所 有 参 数；vˆt+1(·)为 预 测 值；vt+1为真实值。

3 实例分析

实例中以2011—2019 年美国的相关民航运输数据构建机场网络并对其进行航班延误预测，验证STGCN 用于预测机场航班延误的可行性。

3.1 机场网络构建

在美国选取51 座主要大型机场，将所选机场作为节点，通航航线作为边构建机场网络。美国本土的机场网络如图3 所示。

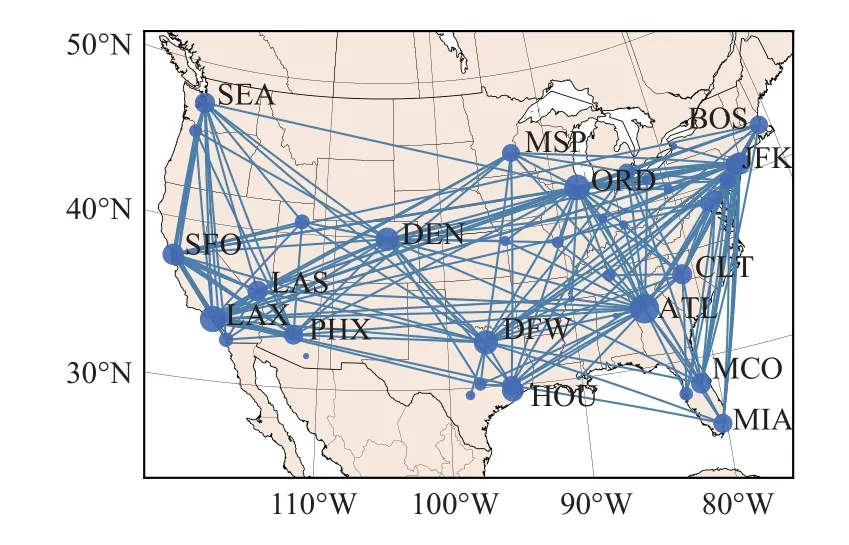
图3 机场网络Fig.3 Airport network

图3 中蓝点表示机场，蓝点越大，表明旅客吞吐量越大，其中所选机场的年旅客吞吐量多数大于1 000 万人次；蓝线表示相应机场之间的航线连接，图中显示的连线均是日航班量大于或等于10 的航线。

图4 为机场网络邻接矩阵W的可视化形式，采用LabelEncoder 对所选机场按照其三字码首字母顺序进行编码。右侧的彩色条说明了W中各节点间的权重区间在 [0,1]。权重越大，颜色越深，相应机场之间的联系越紧密。当权重为0 时表示相应机场间没有航线连接。

图4 机场网络邻接矩阵W 可视化Fig.4 Visualization of adjacency matrix W in airport network

3.2 延误数据采集

所选51 座机场的航班延误数据来源于美国联邦航空管理局（FAA），其中包括了2011—2019 年这51 座机场共计167 631 条航班延误信息，选取机场离港准点率为延误观测值和延误预测值。机场离港准点率是指飞机在预计起飞时间之后的15 min（含）内脱离跑道起飞的准点率。具体延误信息示例如表1 所示。使用Scikit-Learn 库中Preprocessing模块的 StandardScaler函数对各输入数据进行ZScore 标准化操作。

表1 机场航班延误数据示例Table 1 Example of airport flight delay data

3.3 实验设置

3.3.1 实验环境与参数设置

相关实验算法均采用Python 3.7.0 进行编写；深度学习框架为TensorFlow 1.14.0；处理器为Intel(R)Core(TM) i7-10510U，CPU 频率为1.80 GHz；图形处理器为NVIDIA GeForce MX250；机带内存为16 GB。

选取 2 011—2 019年中前7 年的延误数据作为训练集，第8 年为验证集，第9 年为测试集。在测试集中，历史时间窗口设为7 天，分别预测未来1 天、2 天、3 天的机场离港准点率。在设置模型参数时，最大迭代次数（epoch）设为50；批处理数据量（batch size）设为100；深度学习优化器采用 RMSProp算法；初始学习率设为0.008；学习率衰减设为0.7；时空卷积核的大小均设为2。

3.3.2 评价指标选取

选取平均绝对误差（mean absolute error, MAE）、平均绝对百分比误差（mean absolute percentage error,MAPE）、均方根误差（root mean square error, RMSE）作为评价指标。具体计算公式为

式中：yˆi为 预测值；yi为 真实值；n为预测序列长度。

3.4 实验结果分析

3.4.1 不同模型预测结果对比

实例分析中运用STGCN 预测机场离港准点率，并选择3 种经典预测模型进行比较。

1）历史平均（history average, HA）法：一种经典统计模型，将历史平均交通数据作为预测值。

2）长短期记忆循环神经网络（long short termmemory, LSTM）[21-22]：RNN 的改进模型，能够充分利用长距离时序信息，并且可以保持长时记忆。

3）堆栈自编码器（stacked autoencoders, SAEs）[23]：通过堆叠自动编译器建立，将下一层编译器的输出作为当前层的输入从而形成一个深度网络。

实验结果如表2 所示。可知，当预测窗口分别是1 天、2 天和3 天时，STGCN 相比其他3 种预测模型都取得了更好的预测结果。HA 和LSTM 等传统模型并不适用于长期预测。SAEs 由于缺少空间特征的捕获，因此，预测结果相比于STGCN 仍有一定差距。

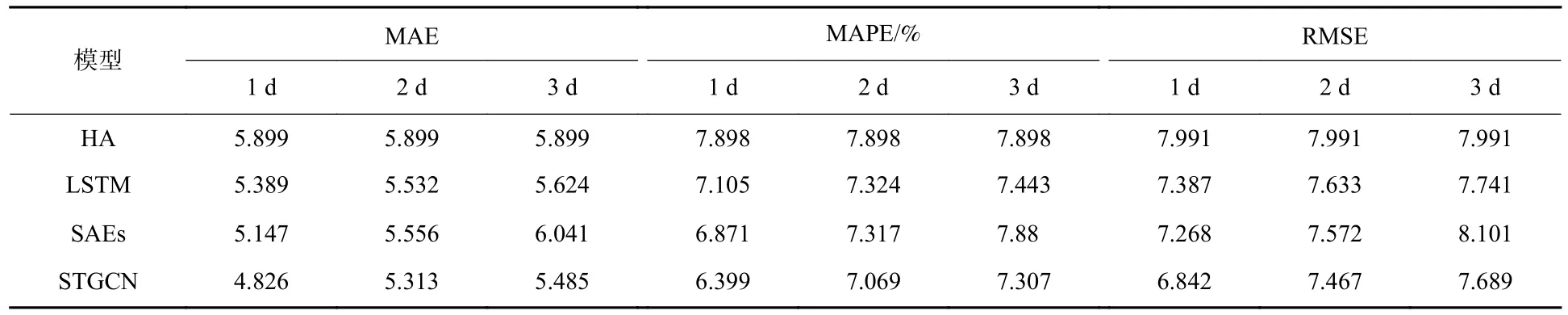
表2 不同预测模型预测结果的评价指标对比Table 2 Comparison of evaluation indexes for prediction results by different forecasting models

图5 为预测窗口为1 天时，SAEs 和STGCN 的预测曲线与真实值的比较，其中预测曲线的数值是当天51 个机场预测值的平均值。可以看出，STGCN的曲线更接近于真实值，说明能够更快速地响应航班延误的动态变化从而更精准地预测航班准点率。

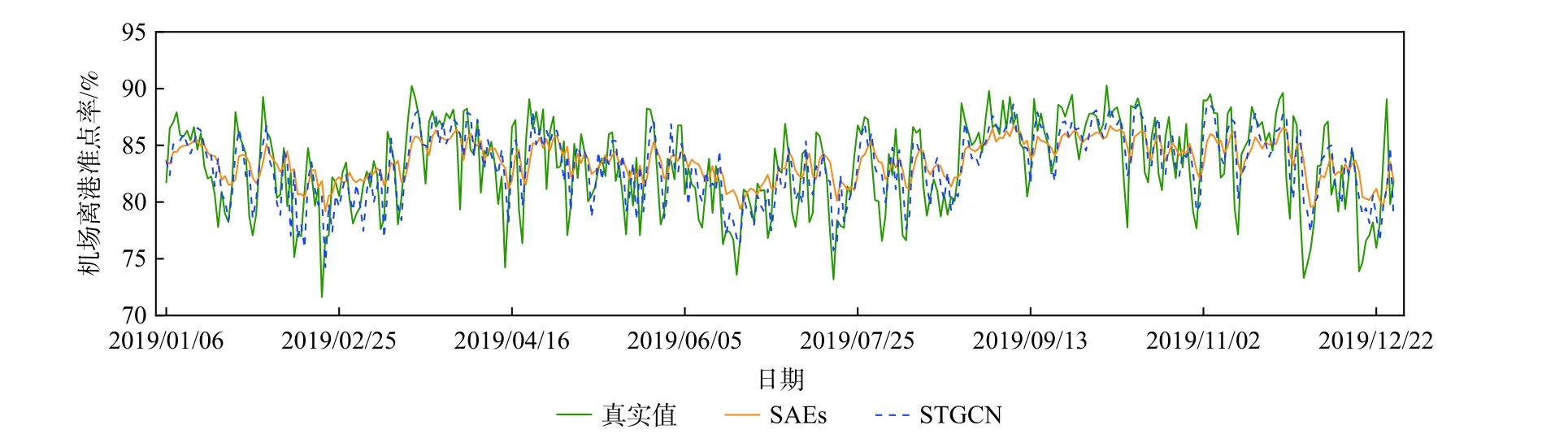
图5 不同预测模型的预测曲线Fig.5 Prediction curves of different forecasting models

3.4.2 不同机场预测结果对比

具体到不同的机场，STGCN 的预测效果也有所区别。选取预测窗口为1 天时，3 座代表性机场的预测结果进行比较，如图6 所示。其中HNL 是所有机场中MAE 最小的，表明预测效果最好；JFK的MAE 处于所有机场的中等水平；MEM 的预测结果不及上述2 座机场，其MAE 为10.54，是所有机场中最大的。结果表明，对于离港准点率波动不大的机场，STGCN 的预测精度较高；而对于准点率波动较大的机场，预测精度会相对下降，但从图6 中MEM 的预测曲线可以看出，对于准点率波动较大的机场仍旧能够较好地拟合出延误波动趋势。

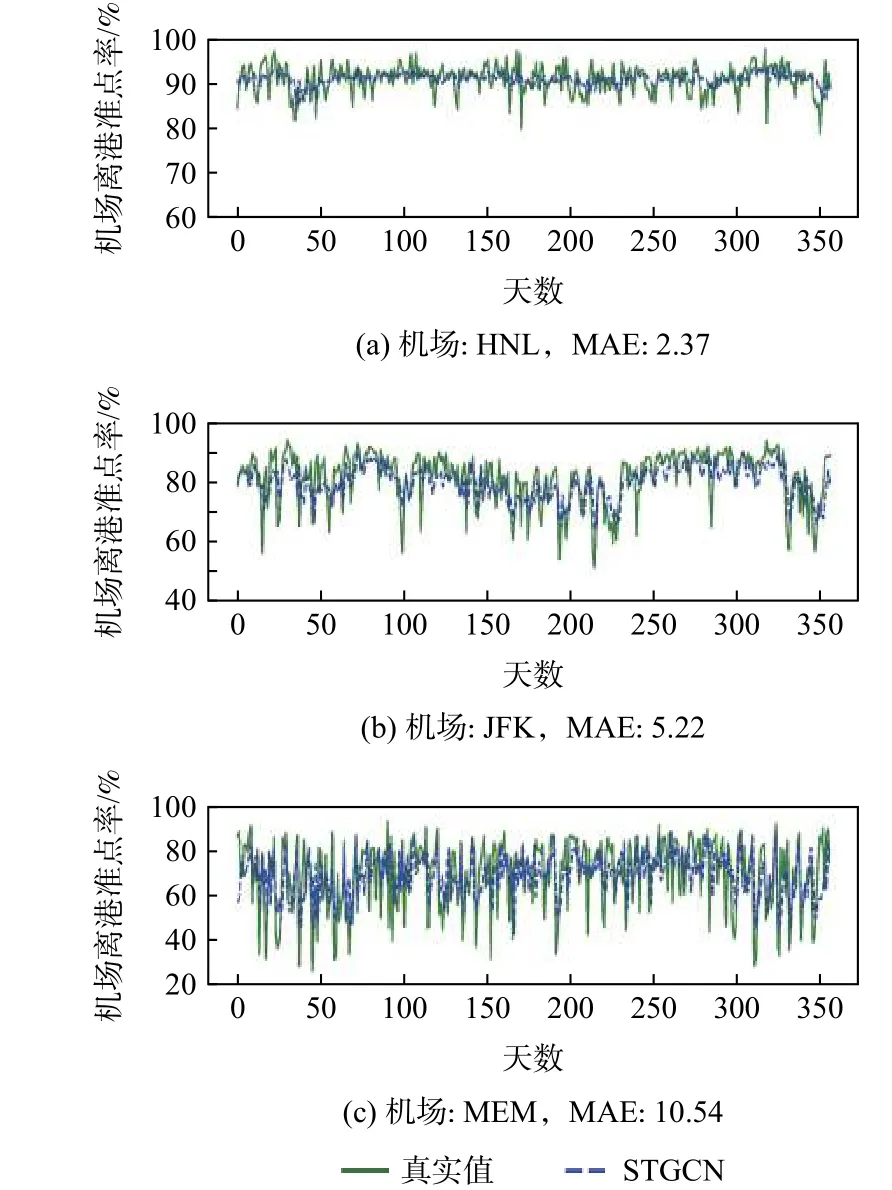
图6 不同机场的预测结果Fig.6 Prediction results of different airports

进一步分析延误预测误差相对较大的机场，发现它们均坐落于人口密集的大城市且都是枢纽机场，与其他机场的通航航线较多，这使得它们的延误不确定性和随机性相比于其他机场更为复杂。

基于此，下文分别从高延误度、中延误度和低延误度3 种机场航班延误程度各自所对应的预测精度出发，说明STGCN 的预测效果。其中低延误度表示当天离港准点率大于或等于 80%；中延误度表示准点率介于50%～80%之间；高延误度表示准点率低于 50%。

图7 为3 种不同延误程度下的各机场航班延误预测误差对比，其中所选的均是一年中发生过高延误的机场。可以发现，在发生低延误时，除了MEM的预测误差较高，其他机场的MAE 均在2～7 之间，表明低延误日的预测结果较好；中延误日的预测误差虽然整体上高于低延误日，但仍处于一个较低的范围，并且中低延误日的预测误差波动幅度较小，表明对航班延误波动趋势的掌握较好；发生高延误时各机场预测结果的MAE 相对较高，并且波动幅度较大，但在这些机场中，除了MEM 的高延误日天数较多，其他机场一年中的高延误日天数均未超过10 天，并且整个机场网络中平均每个机场一年中发生高延误的天数仅为2.59 天。

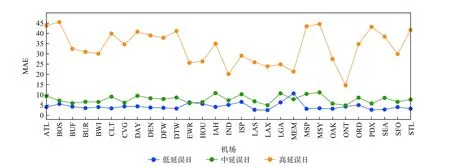
图7 三种延误程度下的各机场预测误差比较Fig.7 Comparison of forecast errors in airports under three delay levels

因此，在未考虑特殊因素导致高延误的情况下，STGCN 在一年的绝大多数时间中能够进行较为精确的航班延误预测，并且快速地响应机场发生航班延误的波动情况。

3.4.3 不同时期预测结果对比

通常航空公司在一年中会多次改变航班计划，这可能会导致航班延误特征发生变化，而航班计划的改变往往和航空运输淡旺季相挂钩，因此，为了更全面地测试不同时期下STGCN 的航班延误预测能力，根据美国运输统计局公示的2019 年旅客吞吐量挑选出全年航空运输的旺季和淡季，并用STGCN分别对旺季和淡季进行航班延误预测。其中淡季是2019 年1 月至3 月，旺季是2019 年7 月至9 月，预测窗口设为1 天。

最终淡季航班延误预测结果的MAE、MAPE、RMSE 分别是5.156、6.984%、7.359；旺季航班延误预测结果的MAE、MAPE、RMSE 分别是4.748、6.293%、6.542。2 个时期的预测结果评价指标和相应的全年指标相近，表明STGCN 在不同时期均能取得较好的预测表现。

进一步分析淡旺季中不同延误程度下的预测结果，参照上文设定的3 种延误程度划分，在淡旺季中按照延误程度分别挑选一天作为测试日。由于2019 年全美没有发生所有机场整体离港准点率小于50%的高延误日，因此，下文主要分析中延误度和低延误度这2 种延误程度，并最终挑选4 天为测试日，分别为淡季中延误日（2019 年2 月17 日）、淡季低延误日（2019 年1 月21 日）、旺季中延误日（2019 年7 月13 日）、旺季低延误日（2019 年8 月20日）。4 个测试日的预测值和真实值对比如图8 所示。

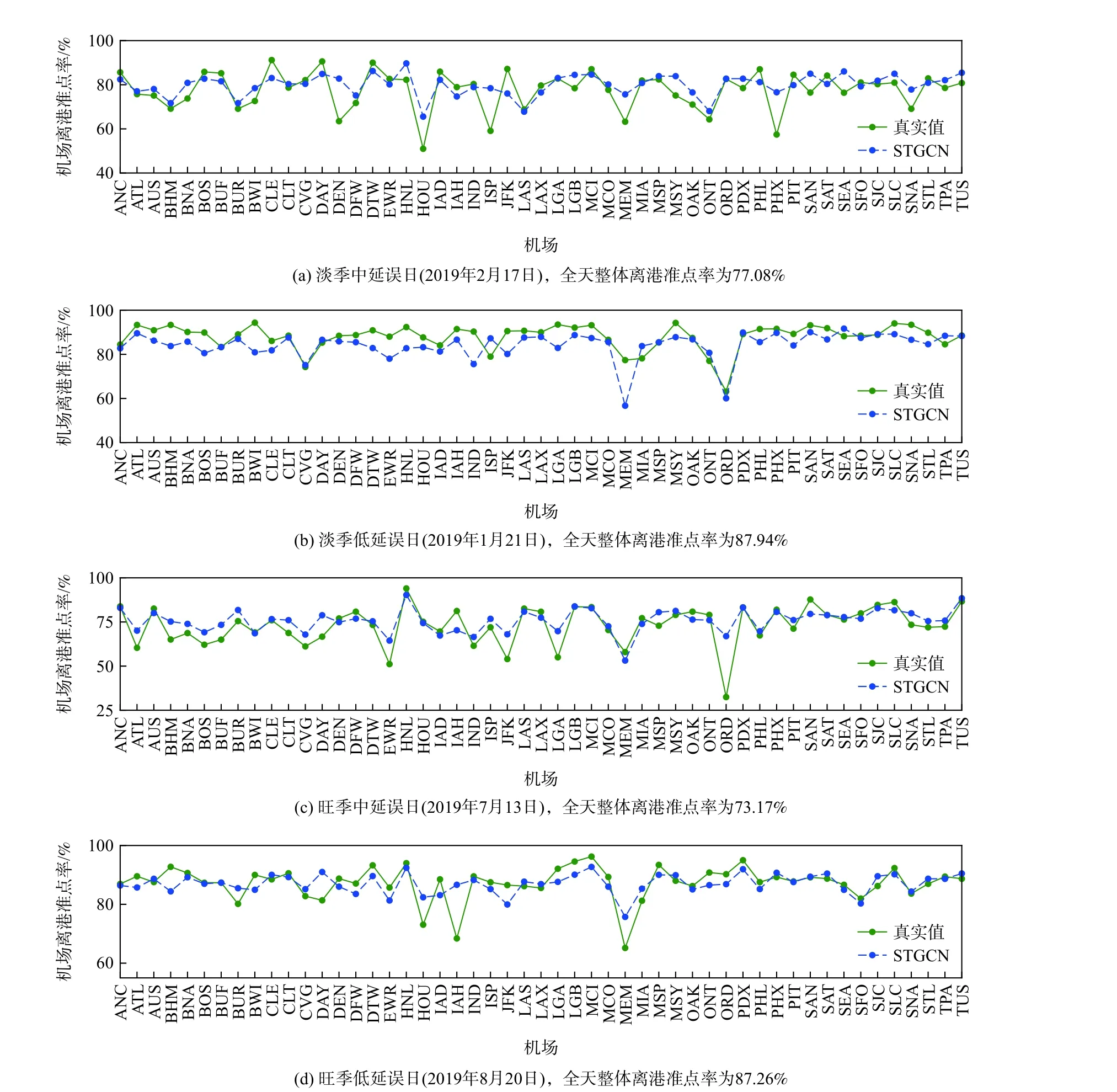
图8 不同测试日的预测结果Fig.8 Predicted results on different test days

图8 反映出在4 个测试日中除了个别机场预测值与真实值相差较大，其他多数机场的预测结果都与实际离港准点率相近，并且可以较为精准地反映出航班延误的动态变化。随后使用SAEs 进行再次预测，以评价STGCN 的预测能力。表3 为2 个预测模型的预测结果评价指标对比，可知STGCN 在4 个抽选测试日的预测结果都优于SAEs，说明在不同时期STGCN 相较于传统预测模型均有着更低的预测误差。

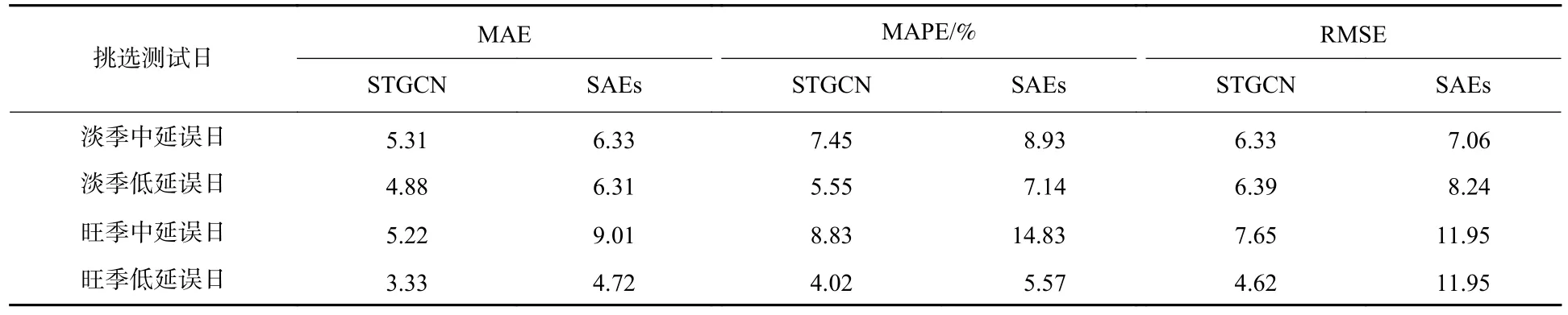
表3 STGCN 与SAEs 预测结果评价指标比较Table 3 Comparison of evaluation indexes between STGCN and SAEs

综上所述，STGCN 在一般情况下拥有较高的航班延误预测精度，其预测结果在一年中的不同时期均有着重要的参考价值和指导意义。

4 结 论

1）STGCN 相较于传统的预测模型拥有更高的航班延误预测精度，并且能够快速地反映出航班延误的波动情况。

2）针对不同的航班延误程度，除了少数高延误日的预测误差相对较大，STGCN 在一年中的绝大多数时间都能保证较小的预测误差。

3）在一年中的不同时期，STGCN 均能做出精准的航班延误预测，为机场制定季节性的航班延误保障措施提供参考价值。

下一步将思考如何引入机场网络中的其他延误影响因素至卷积中。在本文实例分析中发现部分高延误日的预测精度较低，初步分析可能是恶劣天气所导致的大规模航班延误。未来会致力于在模型中引入气象特征，从而进行更为精准的航班延误预测。