油中溶解气体组合预测方案及其在设备状态检修中的应用

叶任时，马书民

（长江设计集团有限公司，湖北 武汉 430061）

0 引言

变压器内部的绝缘油是由许多不同分子量的碳氢化合物组成，一旦变压器内部发生潜伏性故障，放电或过热现象会导致绝缘油中C—H 键和C—C 键断裂，由此产生的氢原子或自由基通过复杂的化学反应迅速重新化合，进而快速形成氢气和低分子烃类气体。特别是，随着故障进程的不断发展，绝缘油中的溶解气体组成也随之慢慢发生变化。因此，分析油中溶解气体的组分和含量是监视充油电气设备安全运行最有效的措施之一。

在此基础上，若能通过大量数据分析归纳绝缘油内部气体含量的变化规律，并在一定程度上对其发展趋势进行预测，则能在变压器内部故障严重之前，甚至在故障发生之前提前安排相关检修，避免可能出现的事故。值得注意的是，电弧放电、局部放电等故障由于具有瞬发性和高能性，不是简单的随机过程，而是混沌过程，只能通过当前油色谱数据进行检测判断，不在预测评估的范畴之内［1］。

目前，国内外已有部分学者针对绝缘油内部的气体量预测开展了相关研究［2-4］，现有研究工作表明，油中气体溶解浓度变化趋势具有一定的规律性或可预测性，但总体而言现有预测方法的精度还有进一步提高的空间［5-6］，而且变压器在不同工况下的油色谱发展规律不尽相同，仅采用单一算法难以保证不同工况下的预测精度，同时当历史油色谱数据出现较大幅度的波动时，单一预测算法会得到误差较大的离散点，方法的鲁棒性有待提高［7］。此外，对于相同的数据样本，单一算法的预测结果可能是正误差（预测结果大于实测值），也可能是负误差（预测结果小于实测值）［8］。因此，针对这样的特征，有学者提出将多种单一预测方法进行组合［9-11］，在某种准则下构建最优化模型，以期实现中和预测误差、减小误差波动范围、提高预测精度的目标。但是，这些组合方法均是针对某一特定应用场景、以固定的几种单一预测方法进行组合，方法的普适性有待提高。组合预测方法的关键在于组合权重的确定，目前有学者通过计算预测误差的协方差矩阵构建最优化组合预测模型，求解得到最优的自适应变权重系数［11］，为本文油气组合预测方案中权重系数的确定提供了有益的启迪。但上述方法采用均方误差作为概率分布预测模型的损失函数，在梯度参量下降时存在学习速率降低的问题。

此外，现有的研究成果绝大部分侧重于预测方法理论的研究，缺乏实际工程场景的应用。在目前的实际运维中，工作人员仅能通过关注状态量数值是否超标来对设备的异常状态进行判断及处理，无法基于预测结果进行设备状态变化的预警。

针对上述不足并结合现场实际情况，本文提出了一种基于信息熵组合的油中溶解气体含量预测方法。首先基于前期收集到的变压器运行数据样本对常用的预测算法进行比较，选取相对表现最优的两种算法建立本文的预测模型，其次利用多信息融合技术，运用信息熵组合预测算法，将选取的神经网络与支持向量机算法进行有机组合，综合考虑多项造成预测误差因素的影响，并运用熵权法分配各因素的权重。最后，通过与常用的最优权重组合预测算法以及原有算法的对比，验证本文所提算法的优越性与可靠性。

1 预测算法简述

1.1 预测算法适应性评价

目前预测算法种类繁多，但不同的预测方法对不同场景具有不同的适应性。为寻找到最适合预测油中气体含量变化规律的方法，本文选取平均误差以及最大误差作为预测方法的筛选指标，其数值上越小，则预测精度越高，对油中气体预测的适应性也越强。其中，平均误差的定义如式（1）所示：

式（1）中，δˉi表示第i种预测算法的平均误差，n表示数据 样 本 的 总 量，ŷij表 示 实 际 测 量 值，yˉij表 示 算 法 预测值。

在此基础上，选择了支持向量机、RBF 神经网络、灰色理论、回归分析、遗传算法、蚁群算法、模糊数学法以及贝叶斯网络这8 种常见的预测算法作为待选算法，并利用收集到的1 000多组油浸绝缘电气主设备正常工况下的运行数据进行预测训练，得到的训练误差如表1所示。

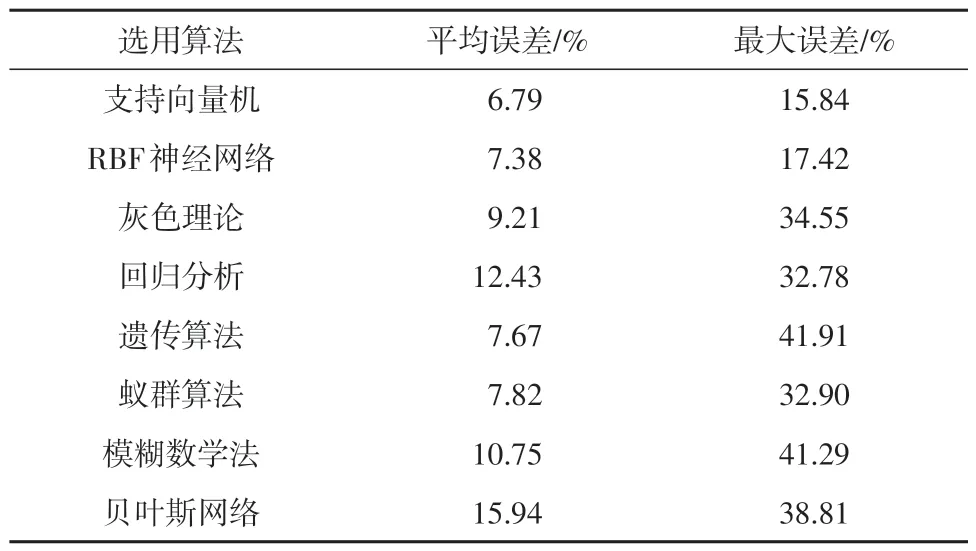
表1 常见预测算法的误差比较Table 1 Error comparison of common prediction algorithms

从表1 可以看出，支持向量机和RBF 神经网络算法在进行油色谱预测时，相比于其他预测方法，预测平均误差与最大误差都能有较优异的表现。因此，本文选用支持向量机与RBF神经网络算法进行预测。

但值得注意的是，并不是所有场景都要选取支持向量机和RBF神经网络预测方法两种算法，也并没有规定只能选取两种方法进行组合。事实上，如果有多种预测方法同时表现得较为优异，此时可以选取多种预测方法进行组合，本文只是提供一个组合预测思路，具体选取方法根据实际场景决定。

1.2 径向基神经网络预测算法

RBF 神经网络属于前向神经网络类型，网络的结构与多层前向网络类似，是一种三层的前向网络，具体如图1 所示［12-13］。第一层为输入层，由信号源结点组成；第二层为隐含层，隐含层节点数由所描述问题的需要而定，隐含层中神经元的变换函数即径向基函数是对中心点径向对称且衰减的非负非线性函数，该函数是局部响应函数，而以前的前向网络变换函数都是全局响应的函数；第三层为输出层，它对输入模式做出响应。

图1 径向基神经网络结构示意图Fig.1 Diagram of radial basis function neural network structure

在RBF 网络中，输入层仅仅起到传输信号的作用，与神经网络相比，输入层和隐含层之间可以看作连接权值为1的连接。输出层和隐含层所完成的任务是不同的，因而它们的学习策略也不相同。输出层是对线性权进行调整，采用的是线性优化策略。因而学习速度较快。而隐含层是对激活函数（格林函数或高斯函数，一般取高斯函数）的参数进行调整，采用的是非线性优化策略，因而学习速度较慢。

RBF 神经网络算法用于点预测时自身需要确定3个参数：基函数的中心、方差及隐含层到输出层的权重，这几个参数会影响RBF 神经网络的泛化性能。RBF的输出可表述为：

式（2）中，N为隐层单元总数，t= 1，2，…，m，m为训练样本总数。

1.3 支持向量机预测算法

SVM 利用回归算法解决预测问题，其中回归算法分为线性回归和非线性回归［14］。其中线性回归给定训 练 样 本 集{(x1，y1)，(x2，y2)，…，(xt，yt)}，其 中xi∈Rn，yi∈R，则回归线性方程可以用式（3）表示：

最佳线性回归函数可以转化为求解式（4）中函数的最小值得到，如式（4）所示：

式（4）中，C表示惩罚因子，ξ、ξ∗表示松弛变量的上下限，且满足约束条件如式（5）和式（6）所示：

式（5）、式（6）中，ξ≥0，ξ*≥0，i= 1，…，k。在此基础上，为求解该最优问题，本文引入Lagrange函数，如式（7）所示。

影响SVM预测精度的主要有三方面因素：正则化参数、不敏感参数以及核参数。其中正则化参数影响了模型的泛化特性，不敏感参数影响了支持向量的数量，而核参数则反映了训练样本数据的分布或范围特性。适当的参数选择可以更精确地对数据进行预测。

2 基于信息熵的组合预测算法

算法的选择只是预测的第一步，为了得到准确的预测结果，还需要对算法本身进行相应的优化调整与改进。不同的函数模型均有其自身对应的参数需要根据数据样本进行拟合，而这些参数需要随着数据样本的变化作出自适应改变，从而更好地对数据进行预测。特别是在训练数据样本不完善的情况下，预测误差将显著增大。因此，需要将不同算法进行有机组合，扬长避短，充分发挥算法的优势，尽可能地减小预测误差。

考虑到影响充油设备油中溶解气体浓度的因素很多，但暂时无法获取完整的相关因素的统计数据，所以仅能划分不同的时间区间（日、周、月），通过分析待预测气体的历史数据来预测其未来发展趋势。事实上，仅用单一预测模型进行预测时，因其考虑角度的局限性、信息选择的片面性以及信息利用程度的差异性，导致其预测精度不高且稳定性差。而组合预测法能很好地综合各种单一预测算法的优势，更大限度地发挥不同方法的优点，做出正确的预测［16］。

经调研可知，目前主要使用的组合预测算法是最优权重组合预测，具体步骤是：对于各种单项预测模块，先计算各自的最优权重，形成组合预测模型，然后加权综合求出最终的预测结果。目前对于最优的标准，多是按照测量误差平方和最小为原则，采用拉格朗日乘子，进行最优权重的计算。然而，最优权重组合预测算法也存在着问题，在计算中往往只能考虑单一因素的影响，因而精度还是受限［17-18］。为了解决这个问题，本文引入了基于信息熵的组合预测算法，该算法可以综合考虑多项因素的影响，并运用熵权法智能分配各因素的权重，使预测精度进一步提高［19］。

熵权法可以综合各预测模型的重要性和指标提供的信息量这两方面更客观地确定各模型的最终权重。某个预测模型的信息熵越小，表示该模型的变异程度越大，所提供的信息量越多，即在整个预测过程中起到的作用越大，其权重也越大［20］。本文采用的组合预测模型使用多种评价指标来评判各单一预测方法的预测精度，评价指标j(j= 1，2，…，q)的重要性熵值如式（9）所示：

式（9）-式（13）中，Nij为各评价指标参数值相对于各评价指标的接近程度，x表示训练样。

由于信息熵e（dj）可用来衡量评价指标j信息的有用程度，信息熵越小则评价指标j的有效程度越高，因此用hj来评价指标j的信息效用程度hj=1-e（dj）。

利用熵权法计算各评价指标的客观权重，实质上是利用该评价指标信息的效用价值系数来计算的，效用价值系数越高，对评价的重要性就越大，于是得到评价指标的客观权重值θj如式（14）所示。

最后，利用上个步骤求出的信息熵，可求出预测方法i的熵权值，即对应的权重值［21］：

由《Q/GDW169-2008油浸式变压器（电抗器）状态评价导则》［22］可知，充油设备内部的绝缘材料在放电或过热情况下，会产生各种特征气体。其中对充油设备故障诊断分析有价值的特征气体主要有氢气（H2）、甲烷（CH4）、乙烷（C2H6）、乙烯（C2H4）和乙炔（C2H2）。这里以H2为例，对其含量进行预测分析。为了比较预测值与实测值，采用预测的相对误差和平均相对误差来评价算法的预测结果，定义如下：

式（16）、式（17）中y为实际监测值，ŷ为模型预测值，n为样本个数。

综上，所提基于信息熵的组合预测算法的具体思路如图2所示。

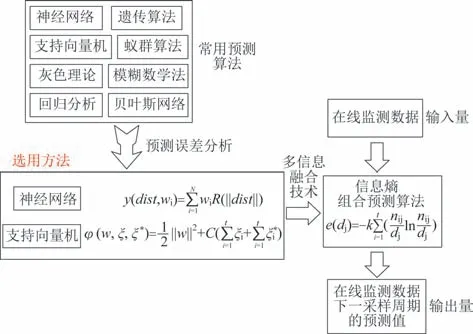
图2 基于信息熵的组合预测算法思路流程图Fig.2 Flow chart of combined prediction algorithm based on information entropy

3 仿真验证

3.1 组合预测方法的优越性验证

为验证所提算法的优越性，本文以北京某220 kV发电厂主变在线监测数据为样本，分别采用RBF、SVM、最优权重算法以及组合算法进行预测。需要说明的是，不同的预测场景存在不同的最优预测算法，然而本文的重点在于比较组合算法相较于单一算法以及传统最优权重算法的优越性，单一预测算法的最适性或者最优权重算法的优化并非本文研究的重点。

在此基础上，本文所采用的在线监测数据以天为监测间隔，使用2017/11/2 至2018/5/10 的数据作为预测模型的训练样本，且数据样本中不包含突变型数据，最终预测未来31 d（2018/5/11 至2018/6/10）H2含量的变化，实际值与预测结果如表2 所示。其中，x表示实际值，RBF、SVM、最优权重算法以及组合算法的预测结果分别以x1、x2、x3、x4表示，各预测算法与实际值的相对误差分别以y1、y2、y3及y4表示。

表2 RBF神经网络和SVM预测模型的预测值与实际值对比Table 2 Comparison between predicted value and actual value of RBF neural network and SVM prediction model

进一步地，各单一预测方法、组合预测及真实值的数值曲线如图3 所示，基于信息熵的预测算法与最优权重组合预测算法的对比结果如图4所示。

图3 基于信息熵的组合预测与单一预测方法对比结果Fig.3 Comparison of combined forecasting and single forecasting methods based on information entropy

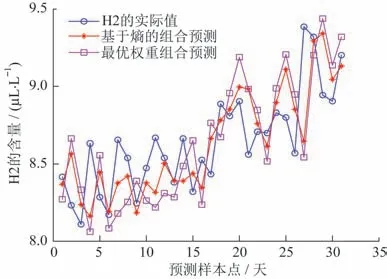
图4 基于信息熵的组合预测与最优权重方法对比结果Fig.4 Comparison of combination forecasting and optimal weight method based on information entropy

结合表2、图3、图4 可知，本项目使用的基于信息熵组合预测算法的平均相对误差不仅远小于RBF 神经网络和SVM两种单一预测模型的平均相对误差，还小于基于最优权重组合预测算法的平均相对误差，因此所提基于信息熵组合预测算法相较于单一算法具有显著的优越性。

3.2 预测结果的实际应用

本文所提出的故障甄别流程是基于预测数据和实际数据的对比，实现对真实故障和运行环境变化所带来的数据突变的甄别，其具体步骤如下所述：

将第N天的实测值与基于0～N-1天的实测数据做出的第N天的预测数据进行比对，如果两者偏差较大（这里设置一个门槛值，为之前预测统计平均误差的两倍，正常的预测不会达到这个误差值。如果出现这个偏差，证明油浸绝缘电气主设备运行出现了变化），存在两种可能，一种是运行工况变化，如变压器突然重载造成预测数据与实测值的暂时性背离。这个重载工况消失以后，后续的实测数据应该将会向基于预测做出的轨线回归。第二种就是实际发生了故障，后续的实测数据将会与基于预测的轨线存在持续性的背离。

基于上述分析，进行第N+1天预测时，应以第N天的预测值而不是第N天的实测值填入预测序列，而预测序列第1～N-1 天的值均为实测值，预测得到第N+1天的预测值。

如果第N+1 天的预测值与其实测值依然吻合，则初步断定第N天的实测值与预测值偏离是扰动引起，则对第N+2 天的预测依然是第N天用预测值，其他天均用实测值来进行预测，如果第N+2 天的预测值与实测值吻合，那么基本可以断定系统未发生故障，且形成的预测序列是可信序列。

如果第N+1 天的预测值与其实测值背离，则初步断定第N天的实测值与预测值偏离是故障引起，这时应该调用故障诊断模块进行诊断，判断出具体故障类型。

如果故障比较严重，变压器停运检修，预测结束。如果故障不太严重，变压器带病运行，在误差允许的条件下，将预测数据窗内全部填入实测值进行预测。也可以将之前的预测序列清空，之后的每一天将实测值填入预测序列的数据窗（一般会用到7 d的数据，每天采集1 个点），直到数据窗填满，具备预测的条件后再启动新的预测。此时可以对带病运行的变压器是否会发生新的故障或经历扰动进行新一轮的判断。

基于上述思路，本文将所提基于信息熵组合预测算法应用于实际场景中，得到以下算例。

3.2.1 算例一

某220 kV 变压器在2014 年7 月20 日出现轻瓦斯保护动作，根据三比值法判断为中温过热故障。实际上该设备在2014年6月25日就出现了总烃含量超标，根据三比值法判断为低温过热故障，但由于产气速率较慢（3.8%），该故障会如何发展未知，因此运维人员并未采取应对措施。本文收集了该变压器前溯1年的油色谱数据，分别采用RBF、SVM以及由本文所提组合预测方法（两种算法组合）对2014 年7 月1 日-2014 年7 月30 日的油中溶解气体含量进行预测，针对每一种方法获取得到的油中气体含量数据系列，采用三比值法判断变压器是否发生故障以及故障类型，三种方法均成功判断出设备将发生中温过热故障的趋势。其中RBF 算法为正误差（即预测状态异常早于实际时间），SVM算法为负误差（即预测状态异常晚于实际时间），预测结果如图5所示（以H2为例）。

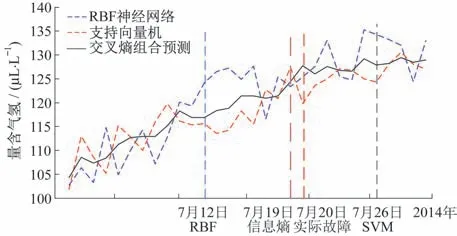
图5 预测对比结果(场景1)Fig.5 Comparison results of prediction (Scenario 1)

由图5中的对比结果可以看出，RBF算法、SVM算法以及组合方法预测设备故障状态跃变为中温过热的时间分别在2014年7月12日、2014年7月26日及2014年7月19日。

RBF算法预测结果相比实际情况提前了8 d，虽然可以更早地发出报警信号，但如果采用RBF算法的预测结果，则运维人员将在2014 年7 月9 日开始调集检修资源，而实际上2014 年7 月12 日设备状态尚未跃变，继续等待至2014 年7 月15 日仍未提示异常，则将会解除检修计划，而到了2014年7月20日设备状态跃变发生时又需要紧急调集检修资源，这样就造成了检修资源的往复浪费，增加了检修成本。

SVM 算法的预测结果比实际情况滞后了6 d。如果采用SVM算法的预测结果进行检修准备，即在2014年7 月19 日才开始调集检修资源，仅仅比故障实际发生时间提前了1 d，因此，该预测算法未达到规避应急检修的目的。

相比上述3 种方法，本文所确定的组合方法的预测结果与实际情况最相近（提前1 d），因此采用组合方法结果能够为运维部门提供最为准确有效的检修提示，弥补了其余单一方法的不足，避免了检修资源的浪费，这也充分说明了高精度预测的必要性。

3.2.2 算例二

再采用另外一组实例来说明预测结果均为负误差的场景。某220 kV 变压器在2013 年4 月17 日出现轻瓦斯保护动作，根据三比值法判断为中温过热故障。实际上该设备在2013年3月8日就出现了总烃含量超标，根据三比值法判断为低温过热故障，但由于产气速率较慢（2.5%），该故障会如何发展未知，因此运维人员并未采取应对措施。本文收集了该变压器前溯1年的油色谱数据，分别采用RBF、SVM以及由本文所提组合预测方法（两种算法组合）对2013 年4 月1 日-2013年4月30日进行预测，结果如图6所示（以H2为例）。

图6 预测对比结果(场景2)Fig.6 Comparison results of prediction (Scenario 2)

由图6中的对比结果可以看出，RBF算法、SVM算法以及组合方法预测设备故障状态跃变为中温过热的时间分别在2013年4月24日、2013年4月18日及2013年4月19日。

RBF算法预测结果相比实际情况滞后了7 d，如果采信该结果进行检修准备，则中温过热故障已经发生时，检修准备工作才刚刚开始，没有达到提前准备、避免应急检修的目的；SVM算法的预测结果相比实际情况滞后了1 d，采信该结果进行检修准备的时间裕度为6 d；信息熵组合预测算法的预测结果相比实际情况滞后了2 d，采信该结果进行检修准备的时间裕度为5 d。

由此可见，当所有预测算法的误差均为负误差时，即预测结果均滞后于设备状态异常的实际时间，则各类预测方法的检修准备时间裕度均受到一定影响，甚至出现了刚进行检修准备时故障就已经发生的情况。但是，在此情况下，组合预测算法仍能保证预测结果与实际结果的偏离程度在可承受范围之内（提前5 d 安排），能够为安排检修提供一定的时间裕度。

类似地，在所有预测方法误差均为正误差时，某些单一方法的检修准备提前量可能过大，在目标日期到达后，接下来的ΔT2天内，仍未能将实际的异常情况或故障工况囊括在内，则检修待命状态解除。但是，几天后设备出现异常工况报警，则需重新调集检修资源，又陷入了应急检修的困局。上述场景直接对应的是场景1 中RBF 方法的预测结果。对于上述风险，某一类单一预测方法的出现概率是最大的，而由于组合方法是基于各类单一预测方法的优化组合，其启动应急检修的风险介于各类单一方法之间。

综上，当各类单一预测方法的误差没有呈现单向性（即误差有正有负）时，组合方法总体上优于所有参与组合的各个单一方法。当各类单一预测方法的误差呈现单向性（即误差均为正或均为负）时，在某个特定的场景下预测结果不一定最优，但是从统计意义上来说，组合方法可以保证在全局范围内结果最优。

当选择的观测和预测指标恰当时，组合预测方法及其结果的应用方法同样适用于其他电网设备。此外还需指出的是，目前运维人员对预测结果的信任程度可能不高，如果完全依据预测结果，在状态被判定为劣化时提前进行检修，则将造成预测结果无法后验证的后果，即无法确定此次提前检修是否正确、是否过检修。因此，在试运行期间，应该充分累积数据，结合定期检修或其他形式状态检修的结论，验证组合预测方法判别结果的准确性，最终，以保证既不丧失预测功能，又能保证有足够的时间裕度提前安排检修为目标，合理整定ΔT、ΔT1及ΔT2的值。

4 结语

针对单一预测方法在不同场景应用下的局限性，本文提出了一种具备普适性的变压器油中溶解气体含量组合预测方法，并基于该预测方法形成了一套完整的故障甄别流程，最终通过仿真验证形成以下结论：

1）相比于传统的单一型预测方法，本文所提出的组合预测优选方法可以综合考虑多项因素的影响，并运用熵权法智能分配各因素的权重，在预测结果上具有更高的精度；此外，本文所提出的预测方法能根据不同场景选定最合适的预测方法组合，避免了单一预测方法的局限性，保证了预测结果的可靠性。

2）基于所提出的组合预测方案，本文进一步形成了一套基于时间窗的故障甄别流程。相比于传统故障甄别方法呈现的误差单向性，所提故障甄别流程在全局范围内具有最优的预测结果，对现场运行具有指导作用。

3）本文所提出的方法不仅适用于变压器油中溶解气体的预测，同样也可以适用于电力系统其他方面的预测工作。在后续的研究中，宜拓展组合预测方法的应用范围，形成一套完整、普适的工业化应用方案。