基于自适应递推滤波的高压输电线路行波故障定位方法

张 杰，陈玉林，黄 涛，谢 华，徐晓春

（南京南瑞继保电气有限公司，江苏 南京 211100）

0 引言

高压输电线路横跨范围大、沿线环境复杂，线路发生故障的概率较大［1］。输电线路故障可能会造成电网停电，进而给社会生产造成损失，因此快速、精确地定位故障点，对提高供电可靠性和电网安全稳定运行水平具有重要意义［2-3］。

高压输电线路的故障定位目前主要有两类方法：阻抗法和行波法［4-6］。阻抗法是建立在工频电压、电流相量基础上，通过求解系统电压平衡方程计算故障点到测量点的线路阻抗，进而得到故障距离的方法。然而阻抗法的测距精度易受过渡电阻、互感器变换误差、线路参数分布不均匀等因素的影响，实际应用效果不理想［7］。行波法基于测量行波波头到达测量点的时间，结合输电线路长度和行波波速即可实现故障点定位，且不受系统运行方式等因素的影响，因而得到了广泛的应用［8-15］。

目前，实用化的行波测距装置主要采用小波分析法实现行波波头的检测，但小波分析法的检测精度容易受到小波基的诸多因素影响，例如小波基函数的类型以及分解尺度等［16］。而且在实际应用中发现，行波信号采集装置记录的故障行波信号富含大量噪声干扰［17-18］，这些干扰信号的来源主要包括行波采集通道的电气噪声和变电站内电力电子器件的开关噪声。当输电线路在电压过零点附近或者经高阻接地故障时，行波信号的幅值较小，当故障点距离测量点的距离较远时，行波信号受传输过程色散效应的影响会引起波头发生衰减和畸变［19-21］。这些故障条件下的行波波头奇异性较弱，再叠加噪声的影响，小波分析法容易造成波头的错标定或漏标定，导致测距精度损失甚至测距失败［22］。

针对传统行波测距方法的不足，文中基于故障行波信号特性，提出了一种基于自适应递推滤波算法的行波故障定位新方法。根据原始数据估计噪声的分布参数，构建自适应递推滤波器对行波信号进行滤波，最终实现波头标定和故障定位，并通过仿真分析对所述方法的可靠性和精度进行了验证。

1 行波故障测距原理

当高压输电线路上某故障点F 发生接地短路，如图1所示，利用叠加原理进行分析，故障状态可以表示为正常负荷分量和故障分量的叠加。假设故障类型为金属性接地，则故障状态下接地点的叠加电势为零，相当于在故障点F处施加一与该点正常负荷状态下大小相等方向相反的电压-uf。在此电压的作用下，将产生由故障点F向线路两端M和N传播的电压行波和电流行波。

图1 故障行波信号产生原理Fig.1 Principle of fault traveling wave signal generation

行波信号的传播速度和输电线路的基本参数相关，其中地模分量存在着较严重的衰减和参数随频率变化较大等问题，导致行波信号衰减大且波速不稳定，线模分量的波速在不考虑频率的影响时相对比较稳定，其波速计算公式如式（1）［23-24］。

式（1）中，L1和C1分别为单位长度线路的正序电感和正序电容。

实际应用中，为了避免线路参数不准确引入波速误差，一般使用区外故障实测线模分量的行波波速。当位于输电线路两端测量点检测到的故障初始行波波头到达的时刻分别为tM和tN，结合线路全长l和波速度ν，计算的故障位置距离M侧测量点的距离为：

根据式（2）可知，在输电线路参数已知的条件下，不同位置的短路故障，可以通过检测线路两端故障初始行波波头到达时刻来进行定位分析。考虑到高压架空线路的行波传播速度接近光速，因此行波波头的准确标定是影响故障定位精度的关键。

2 基于自适应递推滤波的行波波头检测

2.1 行波信号状态空间模型

输电线路故障时的电气量信号可分解成稳态基波信号、暂态行波信号和干扰信号［25］。其中，稳态基波信号为未发生故障时线路中稳定存在的基波信号；暂态行波信号为故障后由故障点突然产生、向线路两端传播并发生折反射、迅速衰减的故障行波信号；干扰信号即为环境中或系统中存在的噪声等信号。相对于电压互感器，电流互感器能够更好地对高频分量进行传送［26-28］，因此采用电流行波进行分析，则行波信号的状态空间模型可表示为：

式（3）中，ik为测量信号；i0，k为稳态基波信号；wk为故障行波信号；νk为干扰信号。

故障行波信号为宽频域信号，且有效的频率区间位于高频部分［29-30］，高通滤波不会给行波波头的奇异性检测带来不利影响。对实际电力信号进行高通滤波处理，可以去除稳态基波分量和低频干扰，保留故障行波信号的高频部分和系统噪声。因此，经高通滤波后由行波采集装置测量的信号表示为：

式（4）中，iH，k为高通滤波后信号的测量值；wH，k为行波信号高频部分；νH，k为系统噪声。

2.2 噪声分布参数的极大似然估计

故障发生前系统未叠加故障行波信号，此时wH，k为0，iH，k即等于系统噪声νH，k，因此对故障发生前的测量值进行统计可以实现对当前系统噪声状态的估计。

首先对iH，k测量值序列进行窗长为λ的滑动窗口均值滤波，得到均值滤波后数据序列：

设置明显大于噪声幅值的波头阈值，与iλ，k进行逐点比较，得到第1 个超出波头阈值的数据对应的位置即粗定为行波波头位置，然后在此基础上向前剔除一定时间长度的数据以保证不包含行波信号，得到噪声样本数据集：

式（6）中，a为粗定的行波波头位置；b为向前剔除的序列长度。

基于噪声样本数据集W，利用极大似然方法估计当前系统噪声的高斯分布参数：

式（7）中，μ和σ2分别为噪声分布的期望和方差。

2.3 构建自适应递推滤波器

故障发生前系统未叠加行波信号，相邻采样点时刻m和n分别对应的测量值与估计值的残差εm|n的分布应符合噪声偏差值的概率密度分布，此时递推滤波器应滤除噪声的影响；当故障发生时，系统叠加行波信号，残差εm|n的分布将不再满足噪声偏差值的概率密度分布，当采样率足够高，可以观测到εm|n将持续地高于噪声分布区间，此时递推滤波器应立即准确跟随行波信号。同时，为了抑制脉冲信号干扰，本文采用临近三点测量值相对前一点时刻估计值的残差进行综合计算。所构建的自适应递推滤波算法的递推方程为：

式（8）中，îH，k为k时刻滤波器输出的估计值；îH，k-1为k- 1 时刻滤波器输出的估计值；iH，k为k时刻的测量值；Ak为k时刻的滤波器增益。

其中，滤波器增益由以下递推方程给出：

式（9）中，P(|εm|n|)为离散值ω在噪声N(μ，σ2)分布中位于[-|εm|n|，|εm|n|]区间的累积分布概率。

基于所构建的滤波器，预设定初始值îH，1，即可实现对测量值序列iH，k的递推滤波，得到滤波后的行波信号的估计值序列îH，k。

2.4 自适应波头标定

对行波信号估计值序列进行一阶差分计算。

式（10）中，dîH，k为k时刻估计值与k- 1 时刻估计值的差。

以噪声样本数据集对应时间区间内的一阶差分数据最大值乘以一定的裕度系数作为行波波头标定门槛。

式（11）中，icmp为波头标定门槛；r为裕度系数，应大于1。

使用波头标定门槛对行波信号估计值的一阶差分序列进行逐点比较，得到的第1 个大于标定门槛的值所对应的时间即初始行波波头到达时刻。

3 仿真分析

为验证基于自适应递推滤波的行波故障定位方法的准确度与适用性，本文在不同故障条件下进行了仿真试验，并将其行波检测结果、故障定位结果与小波变换的试验结果进行了对比。试验利用电磁暂态仿真软件搭建电网输电线路模型，设置不同故障情况进行试验得到原始电流数据，并对初始电流信号进行加噪处理，进行算法检测试验。仿真模型如图2所示，电压等级为500 kV，线路总长200 km，仿真软件的采样率设置为1 MHz。

图2 输电线路故障模型Fig.2 Transmission line fault model

3.1 行波波头检测算法的实现

以单相接地短路故障为例进行分析，电压故障角为30°，接地电阻300 Ω，故障点F距离M侧80 km。使用截止频率为1 kHz的高通滤波器处理后采集电流行波信号，图3（a）和图3（b）分别为输电线路两端M侧和N侧采集的包含故障行波信号的电流波形。在原始信号上叠加均值为0，方差为0.01 p.u.的高斯分布伪随机数模拟噪声，其电流行波信号如图3（c）和图3（d）所示。

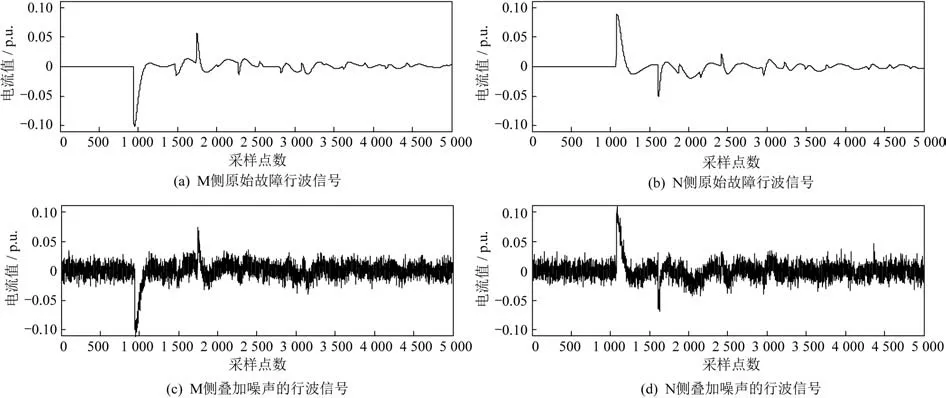
图3 输电线路两端的故障行波信号Fig.3 Traveling wave signals at both ends of transmission line

按31个采样点长度进行均值滤波，设定波头启动阈值为±0.02 p.u.，通过比较均值滤波后信号与波头启动阈值的大小，分别得到M 和N 侧粗定的行波波头位置为942点和1 076点，如图4所示。

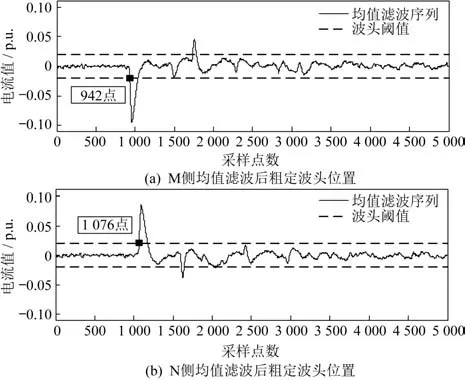
图4 均值滤波后粗定行波波头位置Fig.4 Position of the wave-head with rough alignment after mean filtering

在粗定的行波波头位置基础上，向前剔除固定200 µs 的数据以去除行波波头的影响，得到故障前的噪声样本数据集，根据式（7）基于极大似然估计方法得到噪声样本的分布参数，然后基于式（8）和式（9）构建的自适应递推滤波器对叠加噪声的电流行波信号进行递推滤波，得到行波估计信号。

图5给出了M侧和N侧经递推滤波后得到的行波估计信号，可以看出自适应递推滤波器有效去除了强噪声的影响，而且行波估计信号的峰值没有衰减，输出时间没有延迟，在保留奇异性的同时极大提高了行波信号波头的性噪比。

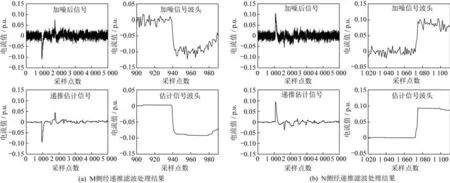
图5 行波信号自适应递推滤波分析结果Fig.5 Analysis results of adaptive recursive filtering for traveling wave signal

根据式（10）对递推滤波器输出的行波估计信号进行一阶差分计算，设定裕度系数为2.0，根据式（11）计算行波波头标定门槛，然后使用行波波头标定门槛与一阶差分序列进行比较实现行波波头位置的精确标定。图6（c）所示M 端经标定的初始行波波头位置为939 点，图6（d）所示N 端经标定的初始行波波头位置为1 072点，这样就实现了输电线路两端对故障行波波头的检测。

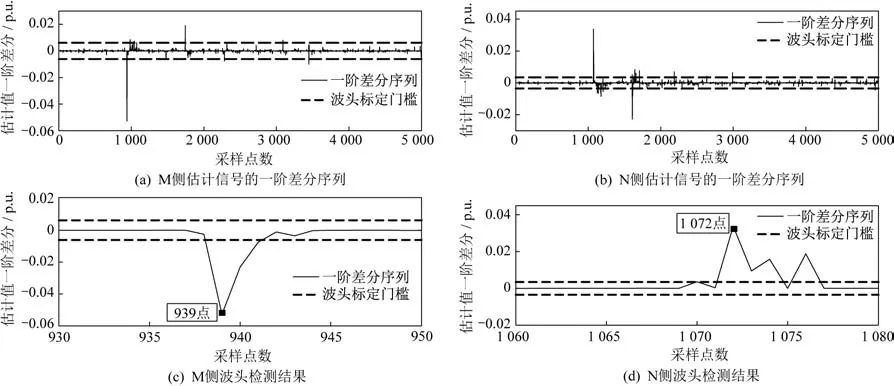
图6 故障初始行波波头的检测Fig.6 Detection of fault initial traveling wave head

3.2 与小波变换法行波检测对比

行波波头的检测精度是行波测距的关键，本文将对自适应递推滤波算法下的行波测距结果与小波变换算法进行对比。为避免行波波速误差的影响，利用区外故障时线路两端检测到的初始行波到达时间差实测得到输电线路模型的实际波速为297 m/µs，后文均采用该波速进行计算。

基于式（2），对前文所述单相接地短路故障，自适应递推滤波算法检测的行波波头时间差为-134 µs，双端测距结果为80.1 km，测距误差0.1 km。

本文选取db3 小波对图3 所示信号进行5 层小波分解，所得到的M侧和N侧信号的第1层至第5层空间尺度下的小波分解结果如图7 所示。结果显示，受噪声影响，在第1层至第3层尺度下无法找到行波波头对应的奇异点。M 侧在第5 层找到模极大值点，点号为929 点；N 侧在第4 层找到模极大值点，点号为1 057点。因此双端测距结果为81.0 km，测距误差1.0 km。以上结果说明，自适应递推滤波算法相对小波变换方法，在强噪声环境下对行波信号的检测具有更高的准确性。

图7 故障行波信号的小波变换结果Fig.7 Wavelet transform results of fault traveling wave

3.3 不同故障条件下的行波检测及定位

为了验证自适应递推滤波算法的适用性，仿真环境中设置不同的故障角、故障距离和接地电阻，以测试不同故障条件下该算法的检测能力和精度。

取接地电阻为100 Ω，故障距离80 km，叠加均值为0，方差为0.01 p.u.的白噪声，设置不同故障角情况下的行波故障测距结果如表1所示。

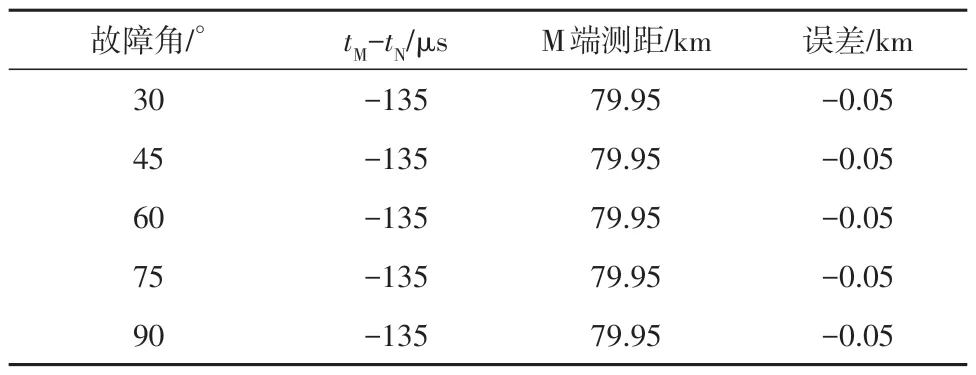
表1 不同故障角下的测距结果Table 1 Location results at different fault angles

取接地电阻为100 Ω，故障角60°，叠加均值为0，方差为0.01 p.u.的白噪声，设置不同故障点位置情况下的故障测距结果如表2所示。

表2 不同故障点位置下的测距结果Table 2 Location results at different fault points

取故障角60°，故障距离为50 km，叠加均值为0，方差为0.01 p.u.的白噪声，设置不同接地电阻情况下的故障测距结果如表3所示。

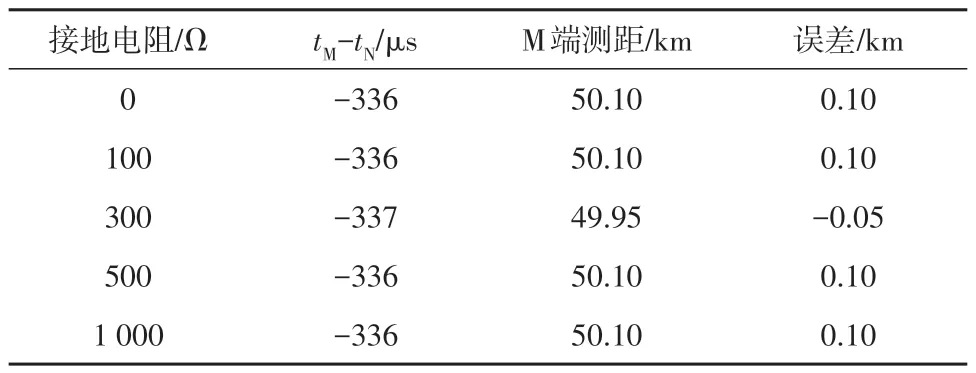
表3 不同接地电阻下的测距结果Table 3 Location results under different ground resistances

根据表1～表3的结果可知，在不同故障角、不同故障位置和不同接地电阻情况下发生的输电线路故障且叠加强噪声时，行波测距的最大误差为0.19 km，说明本文所提出的自适应递推滤波算法在输电线路故障行波信号检测过程中具有很高的适用性和精确度，尤其是为现实电网中存在复杂噪声干扰情况下的行波故障测距提供了一种实用性强、准确度高的方法。

4 结语

本文基于估计的噪声分布参数构建自适应递推滤波器，以实现行波信号检测和故障点定位。仿真试验结果表明，在噪声影响下，自适应递推滤波算法处理得到的行波估计信号波头特征明显，在保留奇异性的同时实现了有效去噪，相对db3 小波变换算法具有更好的检测精度。通过对不同故障情况下的仿真试验，表明自适应递推滤波算法对电网故障行波信号的检测具有良好的适用性和准确性，可以满足工程需求。后期，将重点开展现场实际测试，验证该方法的实用效果。