注重研“形”求“理”,达成解题高效


摘 要:以2021年中考北京卷第27题为例,通过多角度、多方位的剖析,基于多解追求“最佳”;立足多解与系统观的有机结合;注重研“形”求“理”,交融共进,高效达成解题,体现试题的育人价值.
关键词:试题评价;基本图形;解题教学;教学启示
基于中考试题开展解题研究和教学实践是数学教师的基本教学任务,也是提高学生解题能力的基本途径. 教师对中考试题的解读不到位、不深刻,会导致解题教学中的“滑过”现象,学生只能获得问题的答案,而失去了获得解法背后的数学原理和对数学问题本质的感悟的机会,这样的解题教学对试题本身来说仅是管中窥豹、未知万一. 若从试题评价角度切入,深入剖析试题,结合一题多解开展针对性的解题教学,则能有效提高中考试题的教学价值. 基于“双减”背景,解题教学自会走向“减量增质”,力求达到“做一题,会一类,通一片”的教学效果. 笔者以2021年中考北京卷第27题为例,抛砖引玉,浅谈对解题教学的理解与思考.
一、试题呈现
题目 如图1,在△ABC中,AB = AC,∠BAC = α,M为BC的中点,点D在MC上,以点A为中心,将线段AD顺时针旋转[α]得到线段AE,连接BE,DE.
(1)比较∠BAE与∠CAD的大小;用等式表示线段BE,BM,MD之间的数量关系,并证明.
(2)过点M作AB的垂线,交DE于点N,用等式表示线段NE与ND的数量关系,并证明.
二、试题评价
1. 常规出新意,“手拉手”模型巧拓展
此题中蕴含的“手拉手”模型,师生都比较熟悉,但此题把“手拉手”模型与线段中点的论证结合在一起,设计非常巧妙. 特别是第(1)小题证明过程中涉及的结论和全等三角形的性质紧密关联,并隐含第(2)小题的多种论证思路,如BA平分∠EBC,∠EDB = ∠EAB = ∠CAD等,为第(2)小题的论证作好了铺垫,可谓谋篇布局,寓意深远. 第(2)小题把三角形的中位线定理、等腰三角形的性质、全等三角形的判定等多种初中阶段重要的数学知识进行巧妙融合,考查指向基本图形的分离与重构,以及学生的推理能力和运算能力. 同时,检验了学生论证思维构建与解题路径设计的深层次能力.
2. 分解联重构,线段中点拓展思维
几何问题的解决,重在对基本图形的分解与重构.此题具有北京卷中考试题一贯提倡的多路径考查学生拓展思维的鲜明特色,问题看似普通,实则意蕴深远. 线段中点的证明思路颇多,如构造中位线,巧用等腰三角形“三线合一”的性质、全等三角形对应边相等等基本路径. 究其本质,无论采用哪种路径,都需要对基本图形进行分解与重构,即添加合适的辅助线还原基本图形. 从后文提及的几种解法来看,构造辅助线的方法非常巧妙,实则也是通性通法,归根结底是对基本图形的思考和应用. 这也体现了试题设计的初衷,即基于对解题思路构建、尝试、验证和反思的过程,考查学生的思维能力和数学核心素养.
3. 直观促想象,解题过程凸显素养
几何教学应该帮助学生建立分离基本图形的能力,使学生感知、运用基本图形进行思考,借助几何直观和空间想象构建几何问题的数学模型,对问题进行探索,并促进逻辑推理的锻炼与养成. 此题立足旋转变换,聚焦线段中点的拓展应用,通过空间想象达成对学生几何直观素养的培养;立足多种路径解题促进学生逻辑思维多角度、全方位地深度思考与养成. 问题由易到难,思维水平呈进阶式上升,让不同水平的学生立足自身素养基础,达成对应路径的思考与设计,使解题过程成为学生展示素养的舞台.
三、解法赏析
第(1)小题相对简单,主要是为了引导学生经历思维过程,为第(2)小题的论证作好铺垫.
第(1)小题证明:由线段AD顺时针旋转α得到线段AE,可得AE = AD,∠EAD = ∠BAC = α. 所以∠EAB = α - ∠BAD = ∠CAD. 因为AB = AC,所以△EAB ≌ △DAC. 所以BE = DC. 因为M是BC的中点,所以BM = MC = DM + DC = DM + BE.
顺着第(1)小题的结论,根据旋转的性质,容易确定△AED是等腰三角形. 实际上,参照“手拉手”模型,在△EAB ≌ △DAC的结论下,可知证明全等的目的是进一步得出相关的角和边之间的等量关系,于是有∠EBA = ∠C = ∠ABC,即BA是∠EBC的平分线. 另外,还可以得到∠EDA = ∠C和∠BDE = ∠BAE = ∠DAC. 这些重要结论作为基础条件,对第(2)小题的证明起到了至关重要的作用.
第(2)小题结论的判断与证明过程中的思维量较大,具有较好的教学价值,接下来我们将进行重点分析.
在明确NE与ND的数量关系时,学生需要先进行猜想,容易得出NE = ND. 接下来是证明结论,考查学生对线段中点证明路径的思考与选择.
思路1:构造三角形的中位线.
如图2,延长MH,与BE的延长线交于点G. 分离圖形,可以直观看出点N为△BED的边DE的中点,可以通过三角形的中位线来证明,即过点N作NF∥BE交BD于点F,此时,只需要证明点F是BD的中点即可.
要证得点N为DE的中点,NF必是△BED的中位线,也就是点F是BD的中点,即BF = DF. 考虑到已有BM = MC,BE = DC,所以FM =1/2BE. 事实上,学生在思考时,还是会遇到思维的瓶颈,即如何联系FM和BE. 很多学生想到借助BA是∠EBD的平分线,于是延长MH,与BE的延长线交于点G. 此时,根据等腰三角形“三线合一”的性质可以进一步证得∠BMG = ∠G. 又由NF∥BE,得到∠G = ∠FNM,所以∠BMG = ∠FNM,使得FM = FN. 再根据NF =1/2BE,得到FM =1/2BE. 由点F为BD的中点,得到FN是△BDE的中位线,并“解决”问题. 这里出现了把“NF =1/2BE”作为已知条件来使用的情况,这在事实上已经认定NF为△BED的中位线,显然是错误的. 也有个别学生尝试通过先定BD中点为F,再证NF∥BE,试图证明NF为△BED的中位线,显然也是无法实现的.
那么,是不是通过中位线无法证明结论呢?以上构造中位线是通过“先定三角形,再构造中位线”,能否换个角度,先定中位线,再构造三角形呢?具体证法如下.
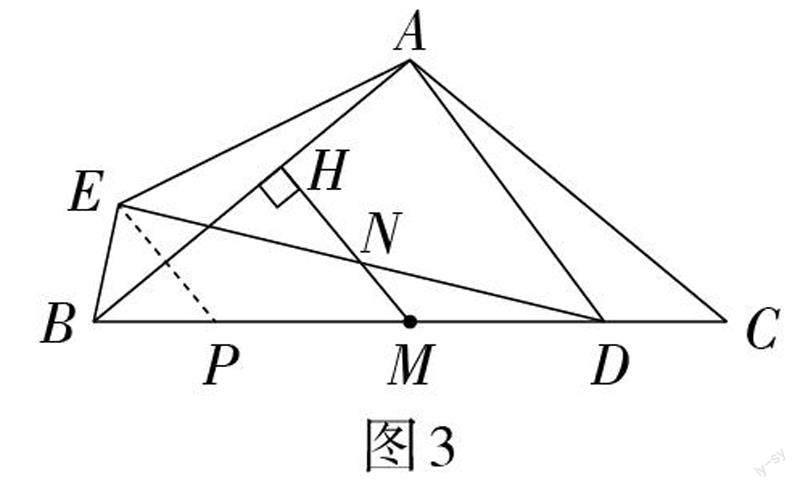
证法1:如图3,过点E作EP∥HM,交BC于点P,
则有EP ⊥ AB.
由已知可得BA平分∠EBD,所以BE = BP.
所以DC = BE = BP.
因为BM = MC,所以PM = MD.
所以MN是△PED的中位线,
故EN = DN.
【评析】构造中位线是证明线段中点的常见思路,关键在于构造合理的三角形和对应中位线. 三角形的中位线既能证明两直线平行,又能证明线段相等. 因此,常见的构造方案:一是定三角形,構造中位线;二是定中位线,构造三角形.
思路2:构造等腰三角形.
从证明点N为三角形一边的中点出发,通过等腰三角形“三线合一”求证也是一种常规路径. 证明EN = DN,可以借助等腰三角形EAD来实现,即连接AN,证明AN是△EAD的边DE上的高线或是∠EAD的平分线.
证法2:如图4,连接AN,AM,易得AM ⊥ BC.
则∠AMC = 90°.
因为AM平分∠BAC,所以∠HAM = ∠MAC.
因为MH ⊥ AB,所以∠AHM = ∠AMC = 90°.
所以∠AMH = ∠C.
因为∠C = ∠ADE,所以∠AMH = ∠ADE.
所以A,N,M,D四点共圆.
所以∠MAN = ∠MDN,∠AND = ∠AMD = 90°,
即AN是△AED的边DE上的高线.
因为△AED为等腰三角形,
所以AN是△AED的中线.
所以EN = ND.
证法3:如图4,由证法2可知A,N,M,D四点共圆.
所以∠MAN = ∠MDN = ∠BAE = ∠CAD.
所以∠EAN = ∠BAE + ∠NAH = ∠MAN + ∠NAH = ∠BAM = ∠CAM = ∠DAM + ∠CAD = ∠DAM + ∠MAN = ∠DAN,
即AN平分∠EAD.
所以EN = ND.
【评析】“三线合一”是等腰三角形的重要性质,也是等腰三角形与“中点”相关问题的解题基本思路. 在等腰三角形的条件下,利用中线、高线和角平分线“知一得二”,构建高线或角平分线证明中线是问题解决的常见思路.
思路3:构造全等三角形.
证明EN = ND,也可以通过全等三角形对应边相等来证.
证法4:如图5,延长MH,交BE的延长线于点G,过点D作DF∥BE交HM的延长线于点F.
由BA平分∠EBC,MH⊥AB,
得∠G = ∠BMG,BG = BM.
因为CD = BE,所以EG = DM.
因为DF∥BE,所以∠F = ∠G = ∠BMG = ∠DMF.
所以DF = DM = EG.
因为∠ENG = ∠DNF,所以△ENG ≌ △DNF.
所以EN = ND.
在构造全等三角形的解题路径下,难以找到构造图形的思路时,常见的方法是构造全等的直角三角形.
证法5:如图6,分别过点D,E作直线HM的垂线,垂足分别为点F,K,延长BE,与NH的延长线交于点G.
参考证法4的结论,易证Rt△EKG ≌ Rt△DFM.
所以EK = DF.
因为∠ENK = ∠DNF,∠EKN = ∠DFN = 90°,
所以△EKN ≌ △DFN.
所以EN = ND.
【评析】利用全等三角形对应边相等实现线段相等(包括线段中点)的证明,是一种常见的证明思路. 解决问题的关键在于利用已有的两条线段,结合已知条件,合理构造全等三角形.
四、教学启示
1. 基于多解追求“最佳”是解题教学的基本要求
对于解题教学,教师常常疑惑要开展一题多解还是只教“最佳”解法. 一些教师认为,没必要一题多解,因为多解中必有“最佳”,只教“最佳”,简洁明了,直奔主题,省时省力;一些教师认为,一题多解能有效培养学生的解题能力,解题时可以有多种方法供学生选择,有备无患. 基于上述对2021年中考北京卷第27题解答过程的研讨,笔者认为,立足一题多解,帮助学生寻求基于自身的“最佳”解法,是解题教学的基本要求. 常说的“做百题不如深研一题”是非常有道理的. 例如,第(2)小题对于3种类型5种证法的研究,通过一题多解能有效触发学生多角度、多方位的思考,全面联动数学知识,促进数学知识体系的有效构建,落实能力与素养的培养. 教学中,基于对以上5种证法的对比与分析,在寻求“最佳”方法的过程中,能有效培养学生的辩证思维,达成深度学习,有效构建数学知识与能力体系.
2. 立足多解与系统观的有机结合是解题教学的关键追求
解题教学中,面对复杂的问题时,我们常常发现教师分析得头头是道,学生则听得一头雾水、唉声叹气. 教师的解题能力很强,教出来的学生解题能力却很弱,是不是我们的教学出了问题?例如,此题第(2)小题的求证,需要学生具备很强的图形重构能力,以及几何直观和空间想象素养,快速解题并不容易. 如果学生已经系统掌握了线段中点的基本证法,那解决问题自然也会水到渠成.
造成学生解题障碍的原因出在哪里?笔者认为,教师未重视多解路径建设与系统观的有机结合是造成学生解题障碍的一个重要因素. 那么解题教学中要如何做好多解路径建设与系统观的有机结合?首先,要做多解尝试,即从不同角度进行思考与解答问题,如此题第(2)小题的5种证法;其次,在解题后要引导学生进行辨析与归类,如将5种证法归纳为3类;最后,将基于线段中点的证法纳入知识和思维系统,与其他知识形成整体构建,建立基于几何直观与空间想象的思维体系,使得以后遇到类似问题时能够快速获得对解题路径的联想,自然产生对基本图形的辨析、分离和重构,从一题多解到多解归一,使解题经验升华到系统思维高度.
3. 注重研“形”求“理”、交融共进是解题教学的核心价值
基本图形在数学解题中有着举足轻重的作用. 但是,到底是侧重于基本图形的“形”的记忆、辨认与运用,还是注重“形”背后的数学原理和深层次的逻辑理解形成“理”的探索更重要?这个问题一直困扰着教师与学生. 笔者认为,几何解题教学既要立足基本图形,又要注重对数学原理的理解和逻辑建构,两者相互融合、缺一不可. 学生的解题能力要通过学习过程的体验,在知识、能力、思维上逐渐达成进步. 通过研究“形”去追求“理”是数学解题教学的本质追求. 因此,在教学中,我们既要培养学生注重对基本图形的“形”的提炼、辨认、分离、联想和重构,也要注重培养学生对基本图形的“理”的探索、理解、诠释、感悟和内化,这样才能使学生的解题能力得到实质性的提升.
参考文献:
[1]郑振兴. 研读试题 分步递增 跳出题海 提升素养:以2018年浙江省温州市数学中考第15题为例[J]. 中学教研(数学),2019(4):21-23.
[2]段志贵. 构造:让解题突破思维瓶颈[J]. 数学通报,2018,57(9):53-57.
[3]郑振兴. 探索解题路径 发展关键能力[J]. 中学数学教学参考(中旬),2021(9):57-59.
[4]蔡卫兵. 思维在多解中提升 素养在探究中发展:一道中考试题的教学运用[J]. 中国数学教育(初中版),2021(5):44-49.
[5]刘志昂. 立足基本图形 追寻多题归一:从一道教材习题及其变式说开去[J]. 中国数学教育(初中版),2018(6):59-62.

