摇摆条件下水平圆管内湍流压力脉动特性分析

朱仕斌，艾华宁

（中广核研究院有限公司，深圳 518026）

核能作为一种高效、清洁能源，在使用安全性、稳定性以及对环境的保护性上具有明显优势以及极大的经济效应［1］。而随着我国“海洋强国”战略的提出，海上小型反应堆对岛屿的供电、供热以及海洋油气开发等具有独特的优势。其作为一种灵活、安全、经济的核电新形式，能够弥补海上能源短缺的问题。因此，发展海上小堆具有重大意义。

反应堆冷却剂流动会诱发堆内构件的振动，即流致振动。长期流致振动可能使堆内构件结构产生疲劳损伤或连接件发生松动、磨损等问题，可能造成事故。因此，堆内构件流致振动理论分析和计算是核电设备安全分析不可缺少的重要内容［2］。

工程经验和大量研究表明，反应堆堆内构件的流致振动主要由随机湍流激励引起［3］。海上小堆在海洋上进行作业时，在海浪、海风等的作用下将引起平台及核电站内的管线产生起伏、倾斜、摇摆等不稳定的运动状态，从而改变湍流运动特性与空间分布，导致压力脉动的频率、幅值发生变化，进而影响结构所受载荷的大小与分布，因此我们需要对海上环境因素重点考虑。目前，国内外针对海洋条件下的流动与传热研究主要集中探讨流速、压降、传热特性等宏观量的变化规律［4-9］，对海洋条件引起的压力脉动的研究较少。

压力脉动主要由大尺度旋涡及小尺度的湍流产生，在一回路流道中，压力脉动主要由湍流引起。本文依据文献［4］实验模型，开展数值模拟，选用该模型的原因在于：（1）有实验数据，便于数学模型的验证；（2）模型简单，压力脉动量均为湍流引起，从而剔除了大尺度旋涡对压力脉动的影响，为完善海洋条件下堆内构件流致振动分析理论提供参考。

1 数理模型

1.1 数学模型

雷诺平均N-S方程方法（Reynolds-averaged Navier-Stokes equations，RANS），大涡数值模拟方法（Large eddy simulation，LES）及湍流直接数值模拟方法（Direct Numerical Simulation，DNS）是目前研究湍流和工程应用的3种主要数值模拟方法。RANS无法捕捉脉动量，而DNS的计算成本太高，因此本文采用LES。LES的基本思想［10］：在湍流数值模拟中只计算大尺度的脉动，将小尺度脉动对大尺度运动的作用建立模型。由于放弃了直接计算小尺度的脉动，数值模拟的时间和空间步长可以放大，从而缓解对计算资源的苛刻要求。

1.1.1 控制方程

守恒形式的纳维-斯托克斯方程（Navier-Stokes equation，N-S方程）如下［11］：

式中，τ —粘性应力张量；

ρ—密度（kg/m3）；

u —速度矢量（m/s）；

t—时间（s）；

P—压力（Pa）；

g —重力加速度。

式（2）是通过分子粘性τ将能量耗散。只有当涡足够小（小到Kolmogorov尺度时）时，分子粘性才算足够大，能将涡耗散掉。

LES中，通过增加一个额外的应力项（亚格子应力）来增大耗散，且能够达到恰好耗散掉大于网格的涡的要求，此时N-S方程变为：

式中，τsgs—亚格子应力张量。

在亚格子模型中，普遍采用涡粘模型进行计算：

式中，vsgs—亚格子粘性；

ksgs—亚格子湍动能（J）；

—变形率张量；

δij—狄克拉函数。

采用该模型后，还存在一个未知量（亚格子粘性，vsgs），各亚格子模型的区别在于对亚格子粘性的计算方法不同，主要有Smagorinsky-Lilly子模型，WALE子模型，WMLES子模型。

本文中采用WALE子模型，该模型是在原始的Smagorinsky-Lilly模型基础上，通过修改速度尺度来解决粘性子层中亚格子应力不为零的情况。

1.1.2 惯性力模型

流体与实验回路壁面的相对速度是影响流动与传热特性的决定因素，而不是流体相对于地面的绝对速度［12］，因此我们需要确定非惯性系下的动量方程，惯性坐标系（O0X0Y0Z0）与非惯性坐标系（oxyz）如图1所示。

图1 惯性坐标系与非惯性坐标系Fig.1 Inertial & non-inertail coordinates

通过建立惯性坐标系与非惯性坐标系的关系，并将惯性坐标系下的动量方程代入，获得非惯性系下的动量方程：

式中，ao—平动加速度（m/s）；

β —转动角加速度（rad/s2）；

ω —转动加速度（rad/s）；

r —控制体在非惯性坐标系的位置（m）；

ur—相对速度（m/s）。

对比式（4）、式（7），并结合等效原理［13］可知，非惯性坐标系下的惯性力F为：

通过自定义函数（User Defined Function，UDF）将重力及惯性力添加至Fluent的动量源项中。

1.2 物理模型

海洋条件下的实际运动复杂，为六自由度耦合作用的结果。为清晰了解海洋条件下的运动对湍流压力脉动的影响与关系，我们通常研究单个自由度的影响。本文以文献［2］的实验模型作为几何模型开展摇摆运动对湍流压力脉动的数值研究，其摇摆台以及摇摆方式见图2，其中ab段为实验段，bc-cd段为出口段，管路绕x轴进行摇摆运动。管长为4.5 m，管径为0.0345 m。为消除入口段效应，我们取实验段入口1.6 m后的数据进行测量，得到管内MN段（2 m）压力随时间变化的实验数据。

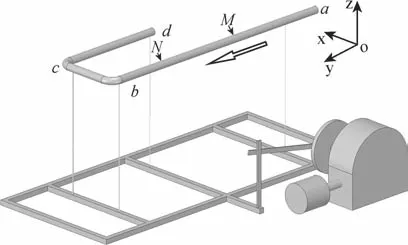
图2 摇摆台及摇摆方式示意图Fig.2 Rolling bench and rolling mode

根据实验段模型，建立如图3所示的数值计算模型。在截面D壁面处均布12个监测点，用于监测压力随时间变化。

图3 数值计算检测面布置图Fig.3 The scheme of measuring sections for numerical calculation

2 数值计算

2.1 计算工况

为获得摇摆周期及雷诺数对湍流压力脉动的影响，我们计算了如表1所示的7个工况，其中前三个工况无摇摆，后四个工况有摇摆。

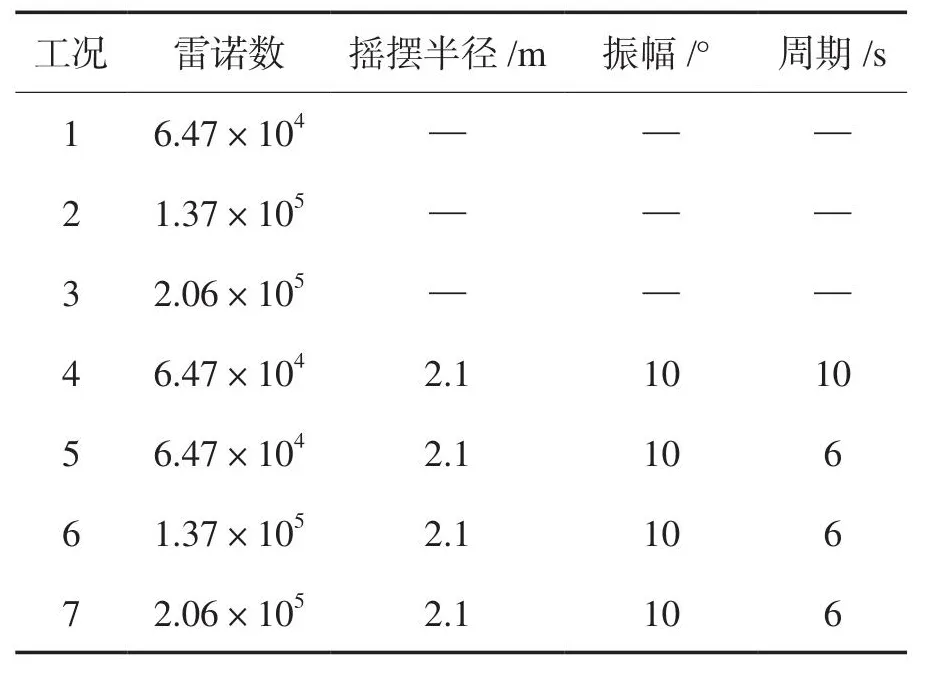
表1 水平管道压力脉动数值计算工况表Table 1 The case table of horizontal pipeline pulsation numerical simulation

2.2 计算网格

水平圆管模型简单，因此本文采用ICEM软件生成结构化网格，如图4所示。为进行网格敏感性测试，以工况1为例，本文计算无不同网格总数下的压力脉动均方根（Root Mean Square，RMS）值，见表2。可以看到，随着网格总数的增加，RMS值逐渐增大，但增长趋势逐渐减小，在综合考虑计算资源与计算效率的前提下，我们最终选定604万的网格进行后续分析。该网格的MN段（关注区）的网格尺寸为1 mm，第一层网格高度设置为9×10-3mm，保证y plus约为1。

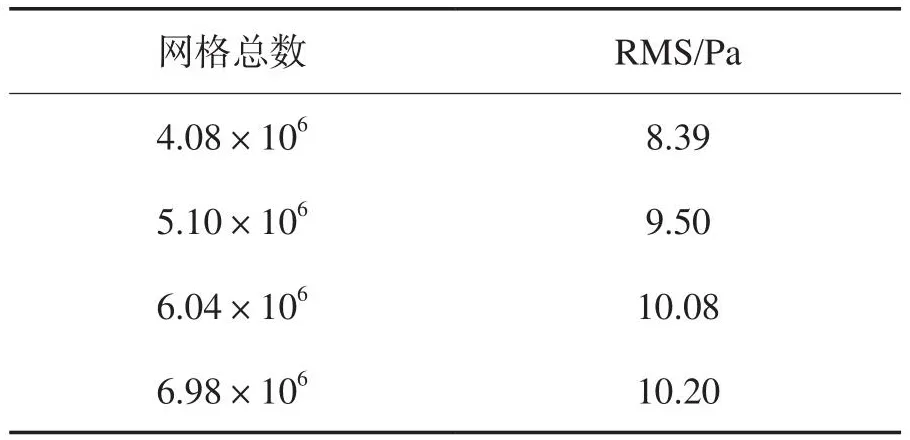
表2 网格无关性测试对比表Table 2 The comparison table of grid independence test

图4 结构网格示意图Fig.4 The scheme of structured grid

2.3 边界条件

管道入口设置为速度入口，管道出口设置为压力出口，壁面为无滑移边界，操作压力设置为一个大气压。

2.4 求解器设置

考虑到流场介质为不可压液体，因此本文采用压力基求解器（Pressure-based solver）。速度压力耦合算法为SIMPLE算法，空间与时间的离散格式均为2阶。

为快速获取瞬态计算结果，本文开始时采用RANS模型进行稳态计算，得到稳态场后生成脉动速度场，以此作为LES的初始值。LES的时间步长应满足每一时间步流体所流过的距离小于网格尺寸，以此得到时间步长为0.5 ms。待计算消除初始效应后，我们将统计量归零，并开启采样，以获取压力、速度等参数的统计量。

3 计算结果分析

3.1 数学模型的验证

图5给出了工况4条件下的MN段压降随时间的变化曲线，其中，参考曲线［8］为数值计算所得，并且采用与本文相同的湍流模型。可以看到，计算曲线、试验曲线［4］与参考曲线相近，因此加载至Fluent的惯性力模型是可信的。数值计算所得结果均表现为后半周期更接近实验值，并且本文计算结果优于参考文献所得结果。

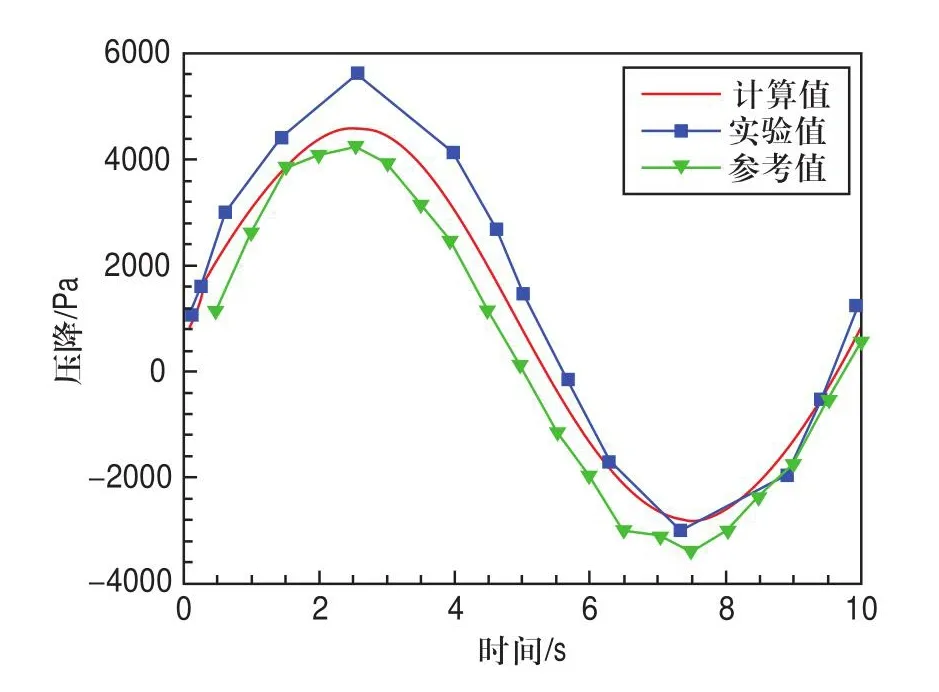
图5 MN段压降随时间变化曲线Fig.5 The pressure drop curve of MN segment with time

3.2 速度场定性分析

图6为工况1、工况4和工况5在不同摇摆相位角下y-z截面的速度分布云图，为便于观察，在后处理时将轴向长度与径向长度的比例按20∶1进行了缩减显示。工况1无摇摆运动，因此本文取1、2、3、4秒时刻的结果进行对比。由于惯性力及重力的影响，我们可以在工况4和工况5的y-z截面上观察到速度场随相位的上下摆动，而工况1则表现出各个时刻下速度场相近。

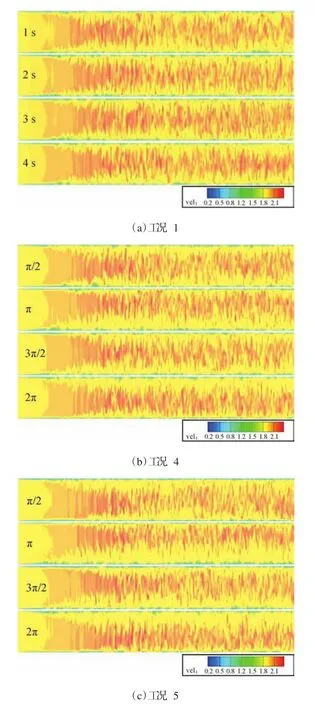
图6 y-z截面速度分布云图Fig.6 The contour of velocity distribution of y-z section

3.3 时域分析

从图6可以看出流体从入口段的均匀来流向湍流转捩的过程。在D截面处，湍流已充分发展。图7给出了工况5在D截面的12个监测点的时程曲线，可以看到，每个节点的压力值在各个时刻均相近，因此本文以D截面的1节点为例，给出不同工况的对比曲线，如图8所示。可以看到，湍流的压力脉动量相对于平均值而言是小量。从图8（a）可知，节点压力的峰值随摇摆频率的增加而增加。图8（a）、图8（c）表明，监测点处压力的响应与摇摆周期是同步变化的。

图7 监测点压力随时间变化曲线（工况5）Fig.7 Monitoring point pressure curve with time（case5）

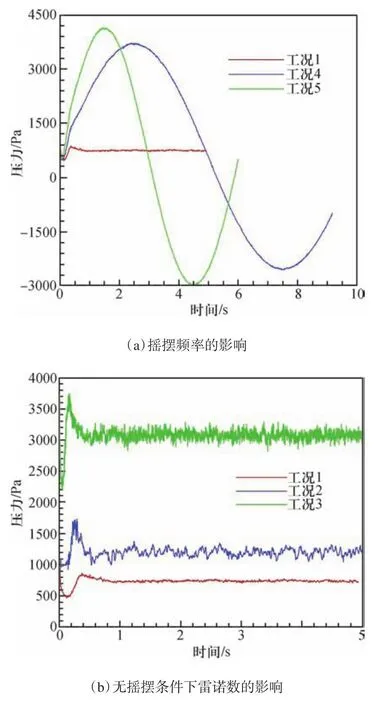
图8 监测点压力随时间变化曲线Fig.8 Monitoring point pressure curve with time

图8 （续）

受摇摆运动的影响，工况4—工况7存在一个与摇摆周期相同的压力波动，该波动是对平均场的贡献，在计算RMS值时需要将平均场的贡献剔除。本文采用高通滤波的方法，将截止频率设置为0.5 Hz（略大于摇摆频率），对所有工况的所有监测点进行滤波，并计算滤波后的压力脉动RMS值，RMS计算公式如下：

式中，pi—预测值，为采样结果；

ai—真实值，被高通过滤器滤掉的波动值；

n—样本总数。

7组工况下12个监测点的RMS值的对比曲线如图9所示。图9（a）为同一雷诺数下不同摇摆频率的RMS值对比图，可以看到，Fluent采样所得结果与滤波后的结果存在偏差，这是对数据进行了滤波所致，该雷诺数下所得RMS均为小量，摇摆频率对压力脉动的影响极小。图9（b）为无摇摆条件下雷诺数倍增后的RMS值对比图，可以看到，随着雷诺数的倍增，工况2的RMS值比工况1增加了约45 Pa，而工况3比工况2增加了约10 Pa，这说明随着雷诺数的增加，其对压力脉动的影响逐渐减弱，从图9（c）也可以得出相同的结论，这与参考文献［14］所述一致。

图9 监测点的RMS值对比图Fig.9 Comparison of RMS values at monitoring point

图10为摇摆和无摇摆条件下，RMS值随雷诺数的变化曲线，可以看到，摇摆条件下的斜率比无摇摆条件斜率大，即摇摆条件的引入增大了雷诺数对RMS值的影响。

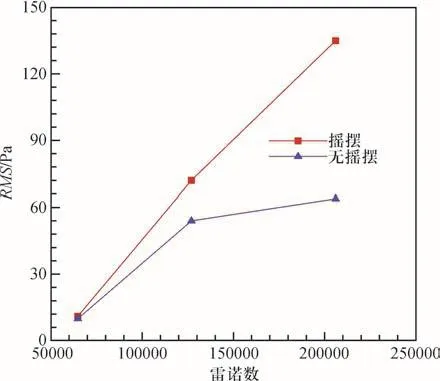
图10 RMS值随雷诺数变化曲线Fig.10 The value of RMS curve with Reynolds number

3.4 频域分析

观察图7可以发现，初始效应在1 s后消失，因此本文取1 s后的样本进行频域分析，为控制变量，均取1~5 s共4 s的采样数据进行高通滤波，后对该数据做快速傅立叶变换，最终可得到各工况下各监测点的功率谱密度（Power Spectral Density，PSD）曲线。从时域分析可知，在同一工况下相同截面上的各个监测点的时程曲线及RMS值相近，其PSD曲线也应相近，因此本文取1节点进行对比，如图11所示。可以看到，压力脉动表现为宽频脉动。对比图9和图11可知，RMS值大的工况，虽然局部PSD值会更小，但总趋势呈现出全频率段的幅值更大，这是因为随着摇摆频率/雷诺数的增加，系统的平均场获得了更多的能量，而该能量又通过能量串级的方式将低频能量传递到高频能量处，直至通过粘性耗散将动能转化为热能，而平均场能量越大，传递给高频的能量就越多，即表现为PSD曲线的幅值越高。

4 结论

本文采用ANSYS Fluent求解器，以水平圆管为例，通过UDF将惯性力模型添加至动量方程的源项中，开展LES数值模拟，并对监测点处的数据进行时域和频域分析，得出以下结论：

（1）相对于平均压力而言，湍流压力脉动值占比极小，表现为监测点处压力时程曲线上出现小的“毛刺”；

（2）观察有摇摆条件的工况发现，速度场与监测点处的压力曲线的波动均呈现与摇摆同步的正弦摆动；

（3）对比摇摆频率的变化发现，RMS值随着摇摆频率的增加而增加，而无论有无摇摆，RMS值都随雷诺数的增加而增加；

（4）对比摇摆及不摇摆工况，随着雷诺数的增加，其对压力脉动的影响将逐渐减弱，表现为斜率逐渐减小，但摇摆条件增大了雷诺数对RMS值的影响。