半悬臂式燃料元件在间隙限制约束下非线性振动的等效方法研究

杨国威，张 勇，宋 勇，凡天娣，陈建伟，林 峰

（1.中国科学院合肥物质科学研究院，合肥 230031；2.中国科学技术大学，合肥 230026；3.中子科学国际研究院，青岛 266041）

与大型核电站相比，小型模块化反应堆具有投资更低、应用场景灵活、模块化设计和固有安全性高等优势［1］。在各种第四代反应堆中，铅基堆具有中子性能良好、传热能力优越、燃料增殖性能优良和固有安全性高［2］等特点，更具有小型化应用前景［3-5］。

近年来，各国提出了多种铅基堆设计方案，包括俄罗斯的SVBR-75/100［6］和BRESTOD-300项目［7］，比利时的MYRRHA项目［8］，欧盟的ALFRED项目［9］，以及中国的CLEAR-I项目［10-12］。目前，铅基堆中燃料元件均采用了下端固定上端简支的结构，该结构可以利用液态铅合金浮力，同时还提供了燃料元件轴向热膨胀裕量。为了提高燃料元件稳定性，添加了中间支撑结构，其中SVBR、BREST-300与MYRRHA采用绕丝结构提供中间支撑，ALFRED采用格架提供中间支撑，代表性铅基堆燃料元件参数见表1。

表1 代表性铅基堆燃料元件设计方案Table 1 Representative lead-based reactor fuel pin design

为了尽量减小反应堆堆芯体积，小型模块化反应堆的燃料元件采用密集型排列。相较于传统铅基堆，小型模块化铅基堆的燃料元件长度大大缩短，可以省略中间支撑结构，并采用上端固定，下端间隙配合的半悬臂结构。与传统的固定方式相比，半悬臂式燃料元件的稳定性略有降低［13］，但减少了安装空间，解决了安装难题。

1 半悬臂式燃料元件非线性振动问题

半悬臂式燃料元件底部间隙导致了燃料元件底端接触变化。接触是一种很普遍的非线性行为，面对接触非线性问题，传统的线性模态分析技术无法得到准确的结果。由于系统非线性因素的控制难度较大，利用实验手段进行的非线性模态研究较少，目前采用的方法大多是寻求非线性模态的近似解解析，因此离散系统的自由度不超过3个，否则，计算量过于庞大。Rosenberg［14］等引入非线性模态理论，主要研究双自由度离散、无阻尼非线性系统的自由振动。堆芯内存在上百根燃料元件，若在多元件抗震分析中完全采用真实的间隙单元模拟，工作量与计算量巨大，为了减少工作量与计算量，根据燃料元件整体动态特性，将下部间隙采用等效弹簧模拟，将接触非线性结构等效为弹簧线性结构。

国际上完成的分析与试验［15］证明，第二阶及更高阶频率对整个元件在地震情况下的总的响应和贡献比例很小。故采用第一阶特征频率等效原则，通过单根燃料元件自由振动分析，将间隙配合悬臂梁等效为弹支梁模型。底端间隙配合半悬臂梁与等效弹簧弹支梁的振动分析模型，如图1所示。常规的等效弹簧刚度计算过程如下：根据悬臂梁模态计算得到的特征向量施加初始平动和转动位移，然后释放，可以得到半悬臂式燃料元件第一阶特征碰撞运动频率，调整代替真实间隙的等效弹簧刚度，当两种不同模型的第一阶特征碰撞运动频率相等时，此时所对应的弹簧刚度即为等效弹簧刚度，此时半悬臂式燃料元件的间隙碰撞效应与等效弹支梁弹簧效应等效［16］。

图1 模型线性化过程Fig.1 Model linearization process

上述方法需要进行多次迭代，无法快速准确地得到等效弹簧刚度。因此，本文推导得到了一种快速准确地计算等效弹簧刚度的方法。该方法具体步骤如下：第一步，结合弹支梁运动方程，建立运动周期与等效刚度关系，确定等效弹簧刚度值；第二步，从单摆碰撞模型入手，逐步等效得到悬臂梁第一阶碰撞运动周期计算公式，进而求解弹簧等效刚度。

2 半悬臂式燃料元件等效刚度求解方法

2.1 弹支梁运动方程推导

第一步，推导得到弹支梁振动方程，确定等效弹簧刚度K的计算公式。

考虑具有弹性控制边界条件的均匀欧拉悬臂梁，如图2所示。其中y（x，t） 是梁在时间t点x处的横向位移，E是梁的杨氏模量，I表示面积的二阶矩，ρ是线性质量。

图2 欧拉弹支梁示意图Fig.2 Schematic diagram of Euler’s bullet support beam

忽略剪切变形和转动惯量效应的均匀弹性，梁的自由弯曲振动运动方程为：

弯曲梁的自由振动方程是一个四阶偏微分方程。求解微分方程，可采用分离变量法，式（1）可以表示为：

其中T（t）是一个简谐函数，可以表示为：

其中ω是系统的固有频率。

式（2）可以表示为：

将式（4）带入式（2），可以得到：

将微分方程式（5）的解设为：

微分方程中有4个参数需要确定，边界条件表示如下。

（1）在固定端，梁的挠度和拐角均为0。固定端的边界条件写为式（7）、式（8）。

（2）在弹性支撑端，梁的弯矩为0，边界条件为式（9），剪力与弹簧力平衡，边界条件为式（10）。

通过上述4个边界条件，解得弹支梁振动方程：

当弹支梁结构确定后，E、I、l也随之确定，根据式（11）可知，只需要确定λ值，即可以求出等效弹簧刚度。是一个与弹支梁运动周期相关的参数，即确定半悬臂式燃料元件的一阶固有频率，便可以求解等效弹支梁弹簧的刚度。

2.2 半悬臂式燃料元件一阶固有频率计算

在半悬臂式燃料元件一阶固有频率求解过程中，采用如下简化方法：第一步，通过假设一个简单的单摆模型来初步估计碰撞运动周期；第二步，根据单摆与悬臂梁的差异，对上一步得到的计算公式进行优化，进而得到带间隙限制的悬臂梁系统一阶固有频率的计算公式。与传统的悬臂梁一阶碰撞运动法相比，该方法在保证计算精度的同时提高了速度。

2.2.1 单摆模型碰撞运动

假设梁质量集中在底端，且梁是刚性的，则悬臂梁模型简化为单摆模型。以单摆模型为研究对象，研究在碰撞过程中单摆小球的运动轨迹，单摆角度为θ0，当左侧转角为α时发生碰撞，模型如图3所示。

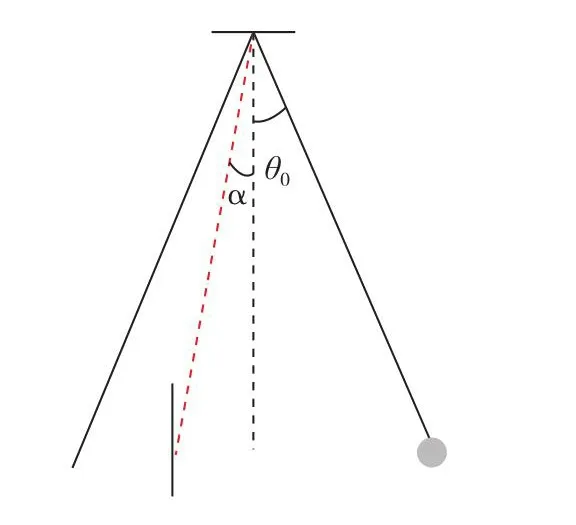
图3 单摆模型Fig.3 Pendulum model

正常情况下，单摆运动质量点的速度曲线与运动曲线如图4所示，当左侧存在挡板时，底端发生碰撞，能量不发生损失，质量点速度在碰撞瞬间方向反向，速度大小不变。

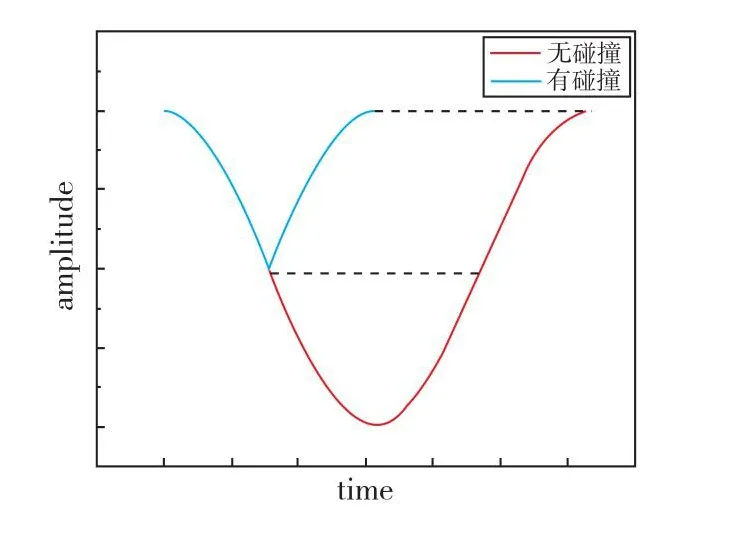
图4 单摆运动轨迹Fig.4 Pendulum motion trajectory

不发生碰撞时，单摆质量点运动周期可以通过式（12）求得，周期仅与单摆长度有关。

其中，l为单摆长度，g为重力加速度。

单摆运动角度与时间成余弦关系：

碰撞状态下的运动周期与夹角α相关。若小球不在挡板左侧运动，则运动的周期减少量即为该部分运动所需要的时间，该部分用时为：

其中ω可以表示为：

此时的运动周期为：

当α=0时，即在中间处设置有碰撞挡板，周期为，即T/2；当α=-θ0时，相当于没有挡板，即为原有周期。在两个极端角度下，根据式（15）可以准确计算单摆碰撞运动周期，初步判断式（15）可以计算不同碰撞角度的单摆碰撞运动周期。

为了进一步验证式（15）的正确性，使用ANSYS中CONTA174&TARGE170单元建立点线接触，构建单摆碰撞模型。单摆模型碰撞点的角度α分别为2°、4°、6°、8°，使用AYSYS与理论公式计算得到单摆碰撞运动周期，见表2。

表2 不同碰撞角度单摆周期Table 2 Pendulum cycles for different collision angles

与通过式（15）理论计算得到的结果进行对比，发现误差小于2%，碰撞角度越大，误差越大，因此得知：式（15）计算结果可靠。

2.2.2 铰接刚性梁模型碰撞运动

为了更接近间隙配合悬臂梁系统，引入铰接刚性梁模型。与悬臂梁模型相比，铰接刚性杆不会发生形变，相较于单摆模型，杆模型质量分布均匀。可以简化为长度为固定点到中心的单摆模型，如图5所示。

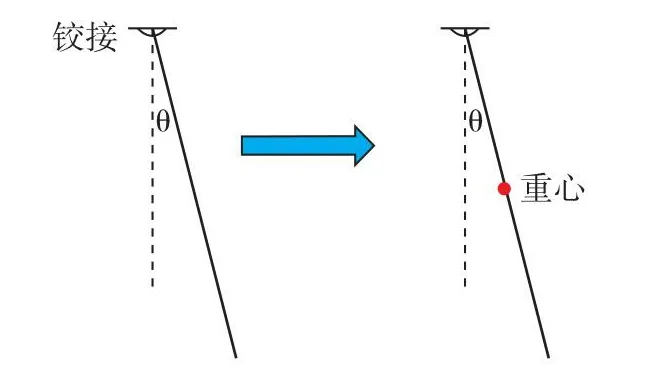
图5 铰接刚性梁模型Fig.5 Articulated rigid beam model

该结构在小角度时，运动形式与单摆一致。

不发生碰撞时，刚性杆末端点运动周期可以通过式（16）求得，周期仅与长度相关。

发生碰撞的运动周期为：

使用LINK1&MASS&TARGE170单元建立质量均匀刚性杆碰撞模型，杆长为1 m，材料为结构钢，摆角为10°。

碰撞点的角度α分别为2°、4°、6°、8°、10°，使用AYSYS与理论公式计算得到的运动周期见表3。

表3 不同角度碰撞单摆周期Table 3 Collision pendulum cycles at different angles

与通过式（17）理论计算得到的结果进行对比，误差小于3%，验证了式（17）计算结果可靠。

2.2.3 悬臂梁一阶自由运动模型

与上两个模型相比，悬臂梁一阶形变自由运动更为复杂，该系统不仅存在动能，还存在悬臂梁的弯曲势能。悬臂梁底端与挡板发生弹性碰撞，碰撞后不发生能量交换，碰撞发生时间极短，可以忽略该过程的悬臂梁形变量。碰撞后，悬臂梁底端速度方向相反，速度大小不发生变化，即碰撞后悬臂梁的动能与势能均不发生变化，碰撞前后悬臂梁端点运动规律可以与单摆等效。

在不考虑底端间隙配合时，本文对悬臂梁进行模态分析，得到第一阶特征频率所对应的特征向量，并将特征向量成比例添加在各单元节点上，作为悬臂梁自由运动初始位移（本文取最大平动位移特征向量为1 mm），初始位移1 mm自由振动的情况下，元件的底端节点位移—时间曲线如图6所示。可以看到其振动基本体现出正弦曲线特性，由于并未设置阻尼，振动无衰减趋势。自由振动的运动周期为0.147 s，频率为6.80 Hz，该频率即为假设悬臂固定时燃料元件的第一阶固有频率。

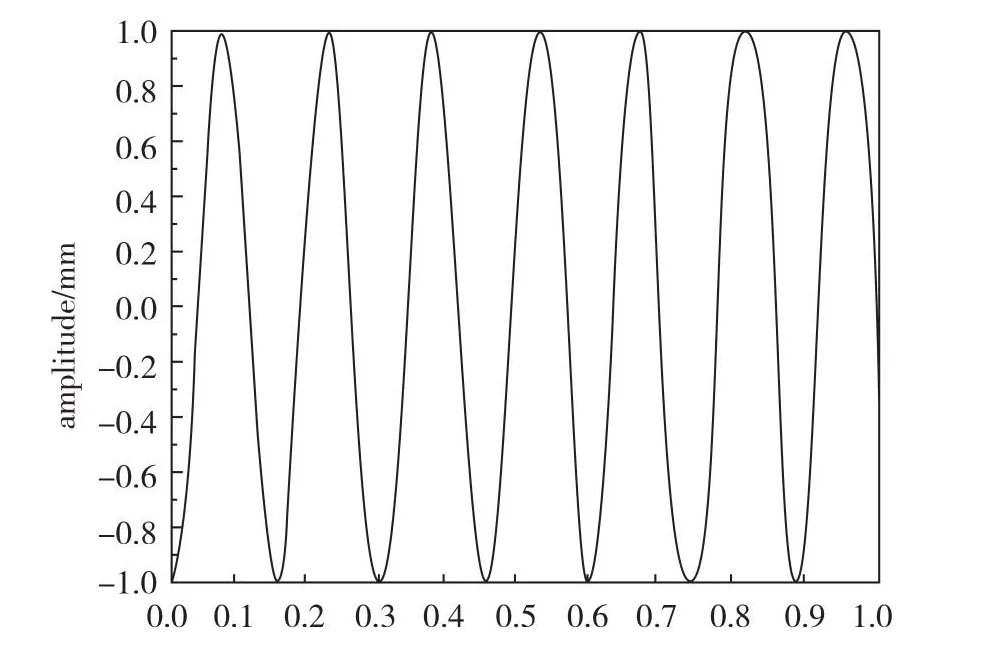
图6 悬臂一阶自由振动底端运动Fig.6 Cantilever first-order free vibration bottom end movement

悬臂梁一阶形变自由运动底端依旧为余弦运动，其振动频率与悬臂梁一阶模态频率一致。

间隙配合悬臂梁结构如图7所示，杆长度为L，间隙为a。

图7 单摆运动模型Fig.7 Pendulum motion model

初始角度θ近似为：

碰撞角度约为：

与单摆模型和铰接刚性梁模型进行类比，得到发生碰撞的悬臂梁运动周期：

其中，T为悬臂梁一阶固有振动周期。悬臂梁一阶固有频率可以由式（21）计算得到。

只需确定悬臂梁一阶固有频率，即可以求得间隙配合悬臂梁系统一阶振动频率。

本文使用BEAM3&TARGE170单元建立点线接触，构建碰撞模型。间隙距离为0.1 mm、0.3 mm、0.5 mm，得到自由端运动轨迹，如图8所示，碰撞点存在位移扰动，可以得到半悬臂式燃料元件运动周期。

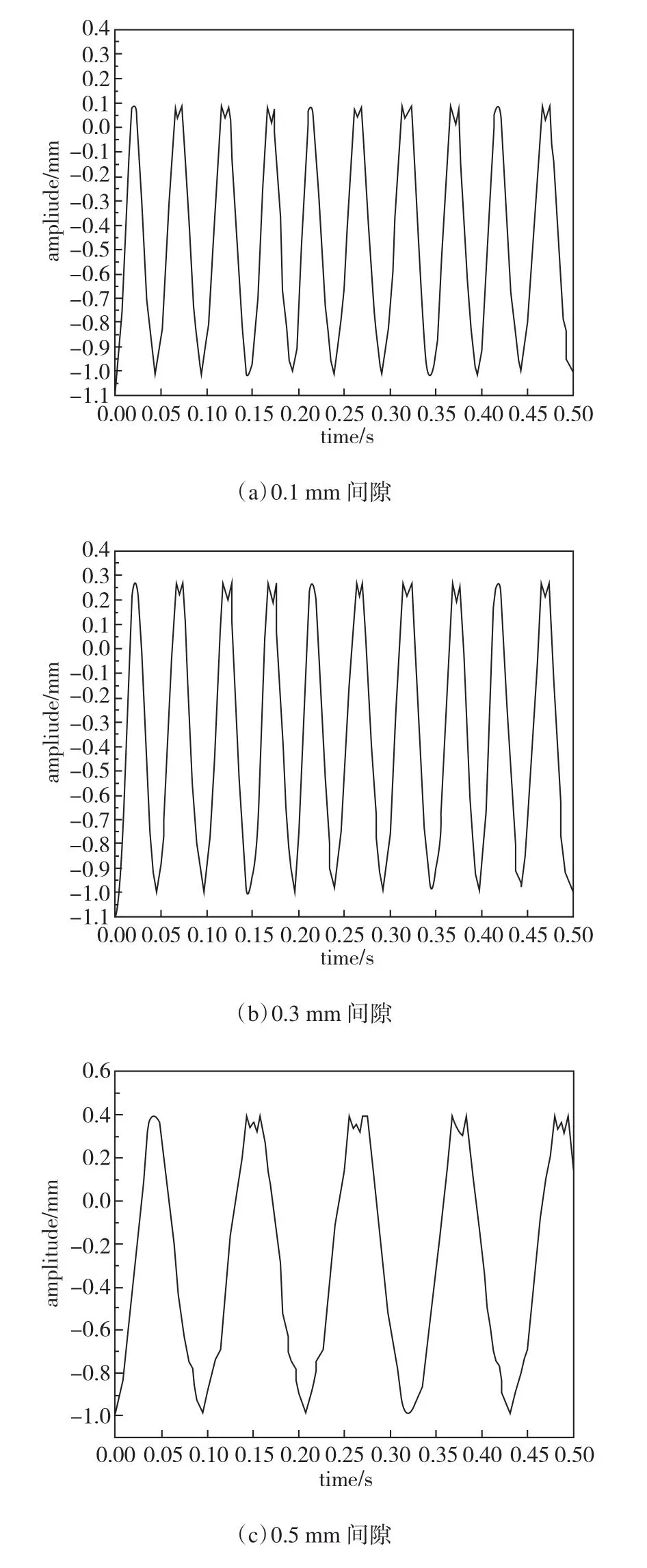
图8 间隙配合悬臂系统自由端运动轨迹Fig.8 Gap with cantilever system free-end motion trajectory

本文使用AYSYS与理论公式计算得到运动周期，见表4。

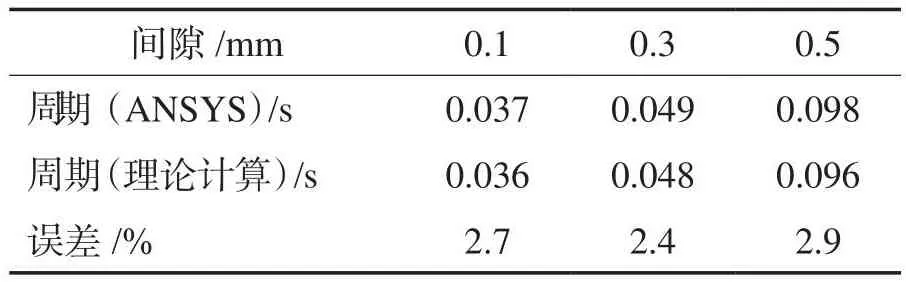
表4 不同角度碰撞单摆周期Table 4 Collision pendulum cycle at different angles

ANSYS计算过程中，发现碰撞时存在抖动现象，且周期均比理论计算长，两者之间误差小于3%，可以通过上述公式快速得到间隙配合悬臂系统碰撞运动周期。

2.3 间隙配合悬臂结构等效刚度确定

得到间隙配合悬臂梁系统振动周期后，结合式（11）可以快速得到弹支梁等效刚度K。计算得到间隙距离为0.1 mm、0.3 mm、0.5 mm时，间隙配合悬臂系统等效刚度的计算结果见表5。

本文使用BEAM3建立悬臂梁模型，并使用COMBIN40&TARGE170对底端进行弹支固定，模型如图9所示。

图9 弹支梁模型Fig.9 Projectile beam model

本文通过ANSYS计算如图9所示弹支梁模型的固有频率，得到不同等效刚度下弹支梁一阶固有频率，见表6。

表6 不同等效刚度的弹支梁一阶固有频率Table 6 First-order natural frequencies of elastic beams with different equivalent stiffnesses

该计算结果与间隙配合悬臂梁一阶自由振动频率对比见表7。

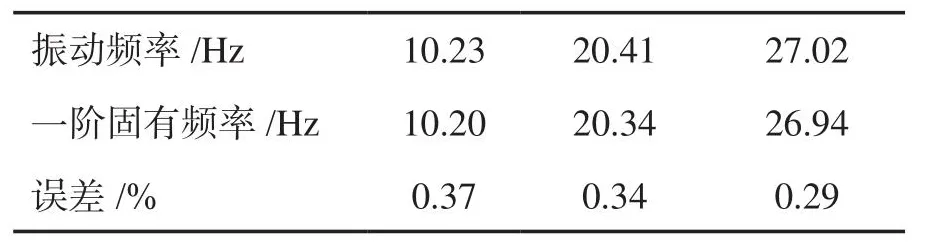
表7 弹支梁与半悬臂梁式燃料元件振动频率Table 7 Comparison of vibration frequencies of bullet support beams and semi-cantilever beam fuel pins

由表7可以看出，两个振动频率基本一致，因此，间隙配合悬臂系统可以使用该等效刚度下的弹支梁进行等效替换。

3 半悬臂式燃料元件抗震分析案例验证

为了进一步确定本方法的正确性，本文对半悬臂式燃料元件与等效弹支梁进行时程分析，分析模型如图10所示。半悬臂式燃料元件底端间隙分别为0.1 mm、0.3 mm、0.5 mm，对应等效弹支梁弹簧刚度分别为1.22×107N/m、1.41×108N/m、5.47×108N/m。

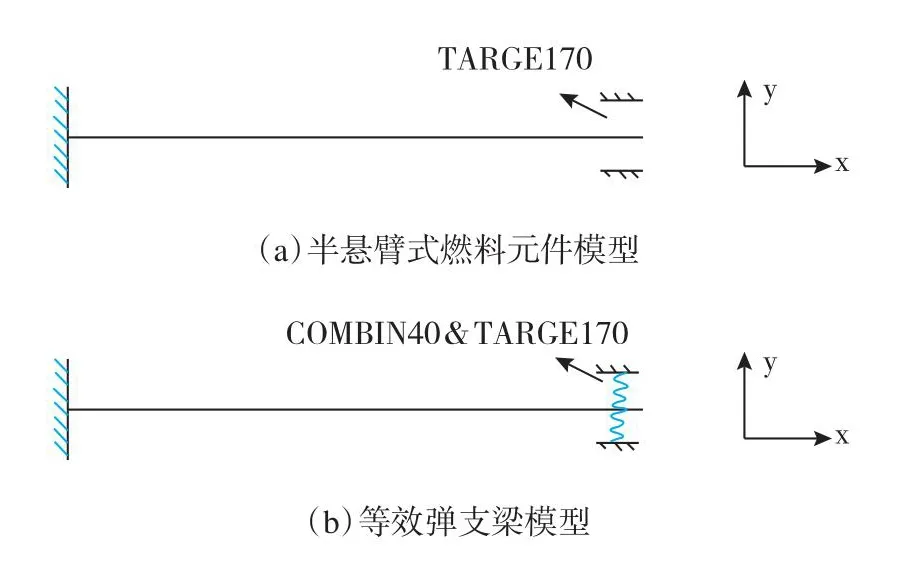
图10 半悬臂式燃料元件与等效弹支梁分析模型Fig.10 Analysis model of semi-cantilever fuel pin and equivalent bullet support beam

本文分别给两个模型在X方向添加RG1.60加速度谱，RG1.60加速度时程谱如图11所示。

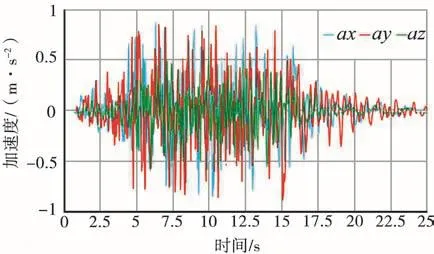
图11 RG1.60加速度时程谱Fig.11 RG1.60 acceleration timer spectrum

本文分别对图10中的两个模型进行25 s的时程分析，时间步长为0.01 s，其中等效弹支梁模型为线性模型，收敛速度快，仅需要17 min；半悬臂式燃料元件模型存在接触非线性，需要用直接积分的方法进行求解，由于所建立的动力学方程的每个对象是最基本的单元，故求解速度和收敛时间较慢，结果文件庞大，计算耗时1258 min（20.9 h）。等效弹支梁模型计算耗时仅为半悬臂式燃料元件模型耗时的1/74。

本文分析得到两个模型最底端位移轨迹，如图12所示。对比两个模型，半悬臂式燃料元件模型与等效弹支梁模型运动轨迹有所不同。由于底端存在碰撞，所以半悬臂式燃料元件底端位移轨迹相较于等效弹支梁模型更复杂，出现大量小幅振动。若忽略这些小幅振动，则两者位移轨迹整体趋势具有一定相似性，且两个模型的最大位移差距较小。

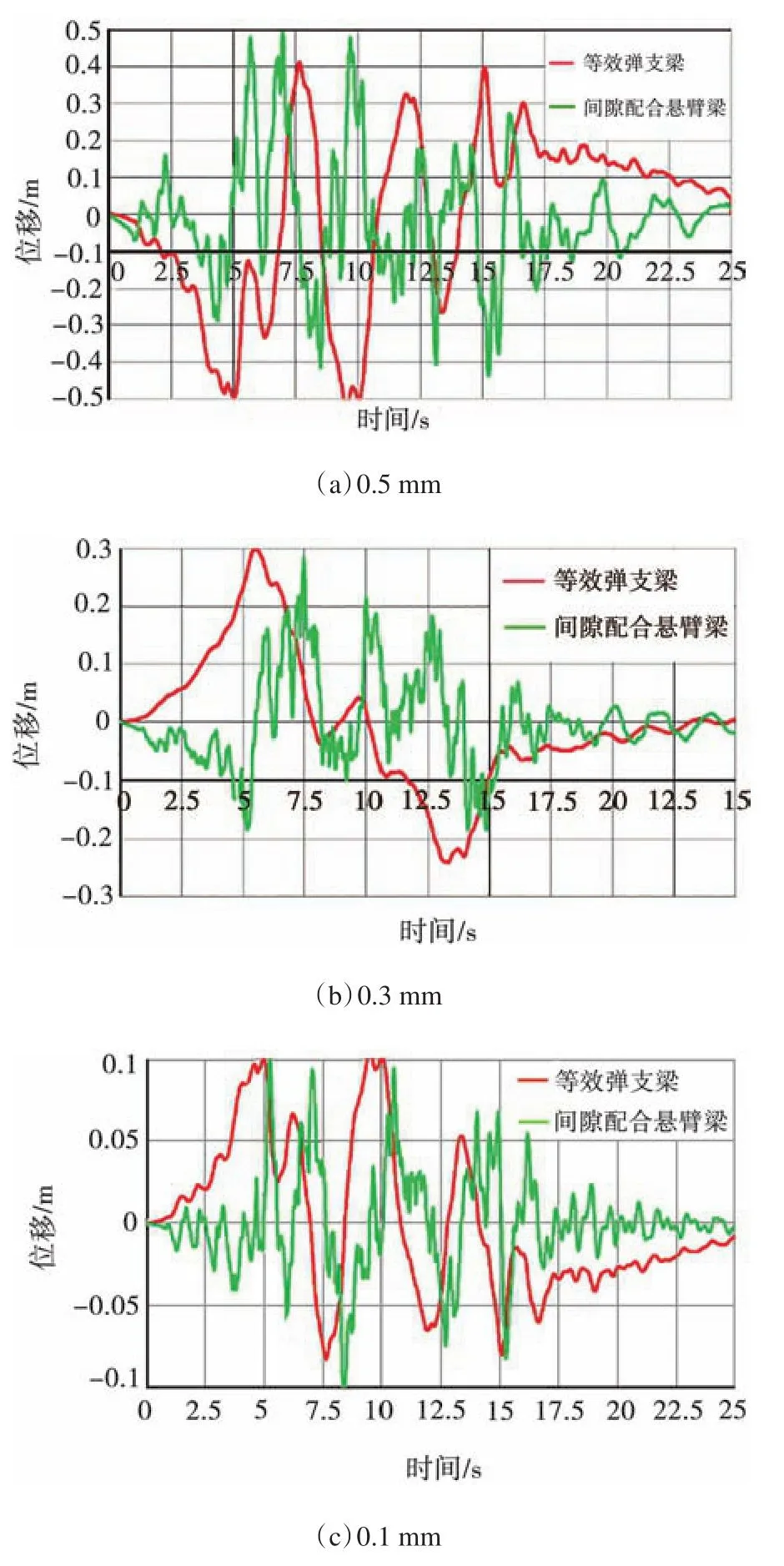
图12 半悬臂式燃料元件模型与等效弹支梁模型底端位移轨迹Fig.12 Semi-cantilever fuel pin model and equivalent elastic support beam model bottom end displacement trajectory

半悬臂式燃料元件模型位移略大，最大位移见表8，不同间隙下两者之间最大位移误差均小于5%，在抗震分析中，等效弹支梁模型可以准确地模拟出半悬臂式燃料元件底端最大位移情况。

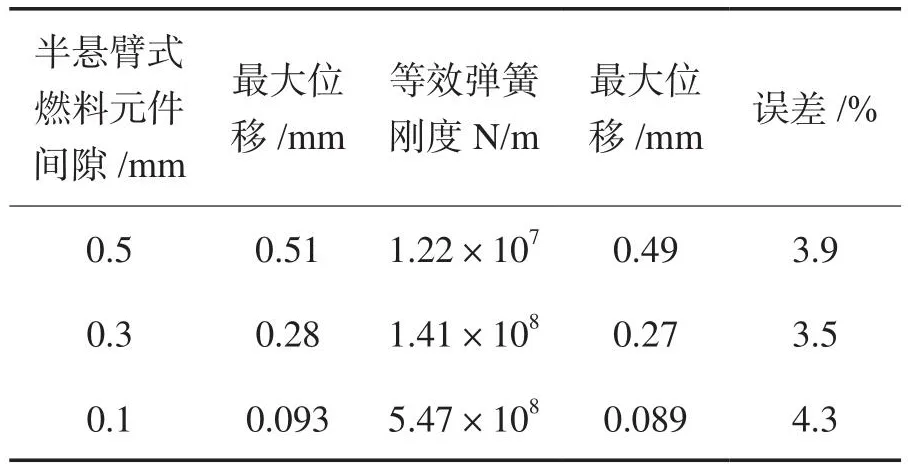
表8 弹支梁与半悬臂式燃料元件与等效弹支梁底端最大位移Table 8 Max displacement at the bottom end of the ammunition support beam and semi-cantilever fuel pin and equivalent elastic support beam

本文分析得到两个模型中间位置位移轨迹，如图13所示。对比两个模型，间隙为0.5 mm时，半悬臂式燃料元件整体呈现悬臂梁阵型，两者存在较大差距。误差随着间隙减小而减小，当间隙小于0.3 mm，且两个模型振型基本一致时，振型更接近简支梁，半悬臂式燃料元件振动依旧更为复杂，最大位移基本相同，等效弹支梁模型可以准确地模拟出半悬臂式燃料元件中间运动情况。

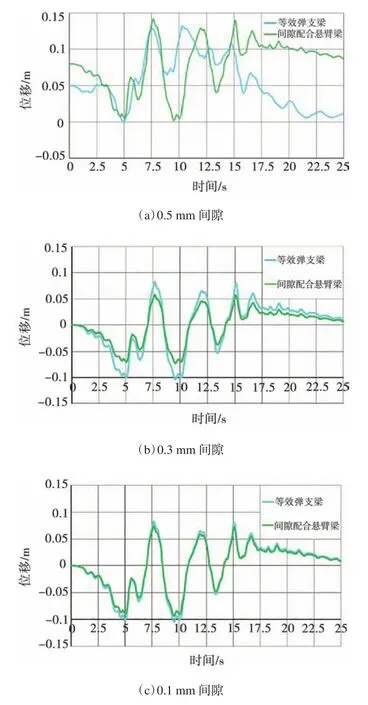
图13 半悬臂式燃料元件模型与等效弹支梁模型中间位置位移轨迹Fig.13 Displacement trajectory in the middle of the semi-cantilever fuel element model and the equivalent elastic support beam model

结合底端位移轨迹分析，可以基本确定，弹支梁与半悬臂梁式燃料元件模型与等效弹支梁模型的运动轨迹基本一致，且在不同位置处最大位移基本一致。

在整个时程分析中，半悬臂式燃料元件模型与等效弹支梁模型最大应变均集中在顶端固定处，不同参数下最大应变见表9，对比得到两模型之间误差小于5%。半悬臂式燃料元件模型与等效弹支梁模型在地震波作用下，受力情况基本一致。

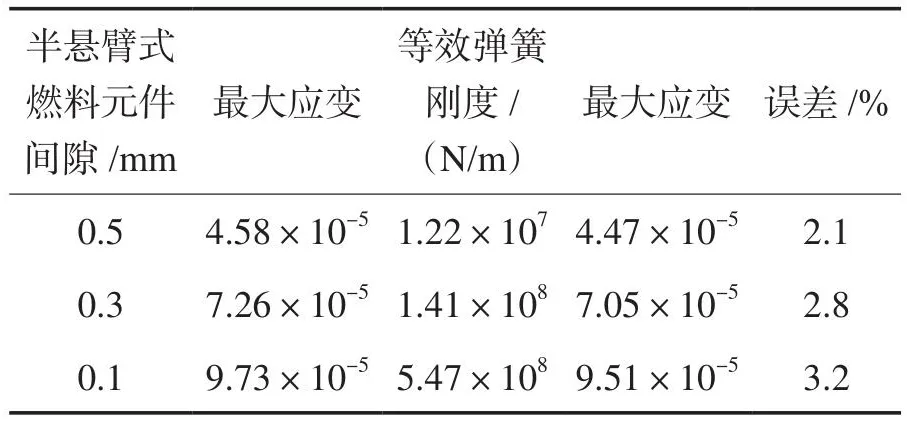
表9 弹支梁与半悬臂梁式燃料元件与等效弹支梁最大应变Table 9 Maximum strain of the ammunition support beam and semi-cantilever beam fuel element and equivalent elastic support beam

综上，等效弹支梁与半悬臂梁式燃料元件模型与等效弹支梁模型位移轨迹基本一致，且受力情况基本一致，两者之间可以相互等效替代。

4 结论

（1） 质量均匀分布的等截面间隙配合悬臂梁系统可以等效为弹支梁结构，进而消除碰撞非线性，大大简化计算过程。

（2） 结合弹支梁振动方程与间隙配合悬臂梁一阶振动周期，可以快速得到弹支梁等效弹簧刚度K，等效弹支梁一阶固有频率与间隙配合悬臂梁系统一阶振动频率基本一致，误差小于3%，通过等效公式，可以快速进行半悬臂式燃料元件在间隙限制约束下的模态分析。

（3） 通过RG1.60时程谱25 s的时程分析，确定等效弹支梁计算耗时仅为半悬臂梁式燃料元件模型的1/74，且关键部位的位移轨迹基本一致，受力情况基本一致，两者之间可以相互等效替代。