浅谈图形与几何教学中如何培养学生的数学推理能力

☉海 华

推理能力的培养首先需要学生牢固掌握已学的知识，在深入理解知识的基础上，举一反三和横纵向对比联系，获得更加开阔的数学知识视野和掌握更加全面系统的数学知识。良好的推理能力有助于培养学生良好的数学思维，尤其是归纳类比能力［2］。结合平时培养学生推理能力方面的教学实践，本文将从以下几个方面例谈如何培养学生的数学推理能力。

一、因材施教，科学制定推理题型

小学数学从启蒙时期的数字认识到后续的计算公式、几何图形，知识点和学习难度逐步提升，教师在小学各个阶段都要制定科学有效的推理能力培养策略，循序渐进地提升小学生的推理能力。对于低段的小学生，数学推理应该侧重于简单的判断；到了小学中高年级，数学推理则需要引入较为复杂的公式推理等［3］。

低段的学生以简单推理为侧重点，即“非黑即白”，类似于简单的判断题。以图形与几何为例，教师为学生展示图形，并让学生自行分辨和判断下一次应该出现的图形，或者是计算不同图形的数量。低段的数学推理，虽然没有涉及复杂的数学知识，但也能培养小学生注重数学推理的素养，从小树立对数学推理的认识。

［案例1］变化的图形

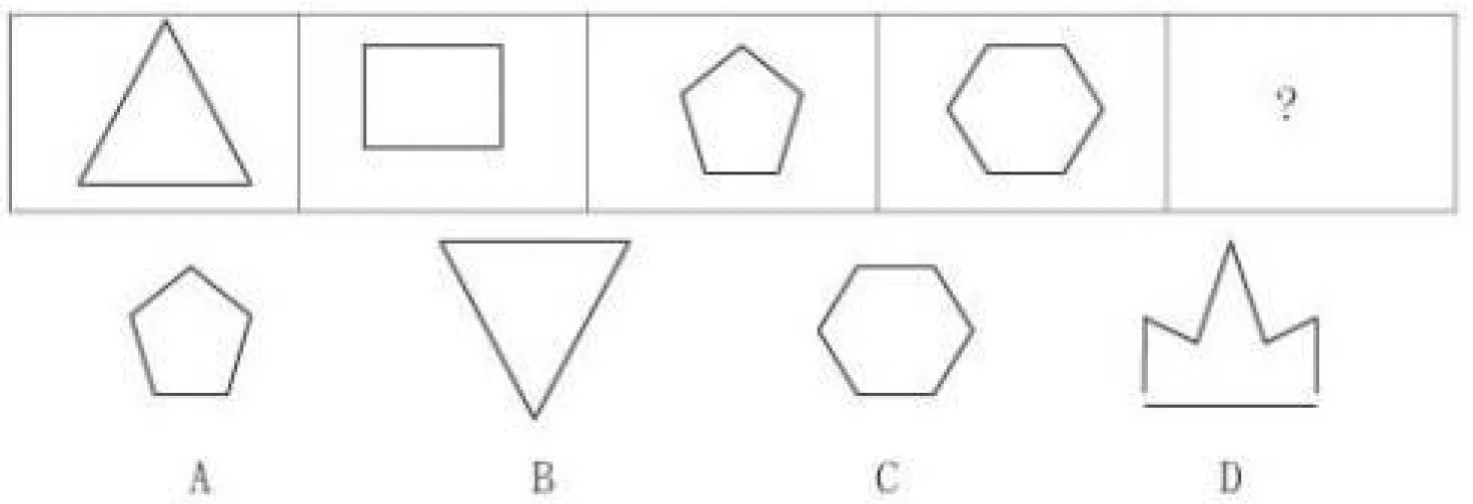
小学低段的学生对几何图形的认知还处于比较浅层的阶段，教师在进行推理训练时，应该选择比较简单、容易推理的题目。例如，这道“变化的图形”题中，让小学生根据已经出现的四个图形，推理接下来的图形［4］。小学生基本上都认识前面两个图形，分别是三角形和长方形，虽然对后面两个图形不是很熟悉，但能够发现它们的边数更多。通过简单地计算这四个图形的边数，学生们就能够得出边数逐渐加一的规律，也就能够推理出下一个图形的边数应该是7，也就是图形D。这种比较简单的推理题，适合于图形认知能力较弱的低段小学生，可以帮助他们从小树立数学推理的意识。

有了小学低段学习的基础，学生的学习能力有所提高，可以进行较为复杂的图形推理，尤其是图形面积计算公式推理。但是，教师在教学过程当中要循循善诱，循序渐进。

［案例2］梯形面积

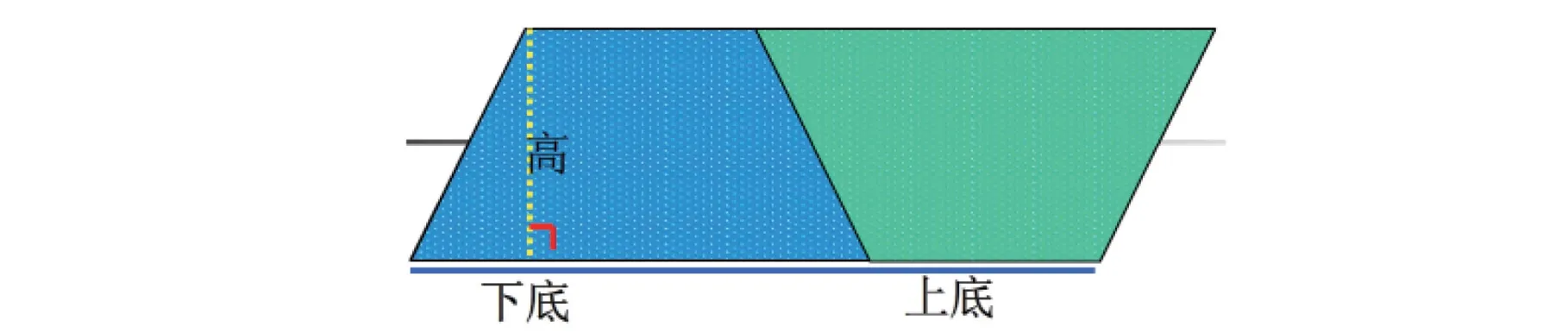
在教学长方形和正方形的面积计算公式后，我给学生画了一个梯形，让他们推理梯形的面积计算公式。学生刚接触梯形，觉得它的形状比较怪异，边长都不相等，而且也不是呈直角，一时间理不清头绪。于是我在梯形的右侧又补画了一个梯形，这两个梯形形状大小完全一样，组成了一个平行四边形。这时，学生就能够推理出梯形的面积计算公式和它的上底、下底、高相关了。根据平行四边形的面积计算公式再除以2 就得到梯形面积计算公式了。这种推理适合于具备一定的图形知识和联想能力的中高年级的小学生。接着，我又画了一个直角梯形，拼上一个相同的梯形后得到一个长方形，学生们对梯形的面积计算公式的理解更加深刻了。

二、强化验证环节，促进合理推理

推理和验证往往是相辅相成的，离开了验证的推理有时会变得虚无缥缈，脱离教学主题，达不到应有的教学效果。部分数学推理还需要对比验证，这也是帮助小学生的数学知识从猜想到确定认知的关键［5］。在验证的过程中，学生能够综合运用数学知识。部分没有确定答案的数学推理可以忽略验证环节，但是能够得到确切答案的推理如果脱离了验证，就会让小学生产生数学是一门感性科学的误解。

实际上，绝大多数的数学问题都是有确切解的。这就要求教师要引导小学生做好推理验证。即使后续的验证结果推翻了之前的推理预期，也是数学应用能力和数学思维一次很好的锻炼。小学生数学推理能力的培养是一项非常重要的教学目标，教师要制定科学有效的教学策略，营造出自由探索思考的学习气氛，加上严谨认真的验证环节，让小学生的数学知识视野和数学思维进一步拓展。

［案例3］圆锥体体积计算公式

在学生学习了圆柱体的体积计算公式后，我给出了一道推理题，要求他们推理出相同规格的圆锥体的体积计算公式：已知圆锥的底面直径d 和高h，如何求体积V？

因为学生第一次接触圆锥体，对圆锥体的概念还不是很清楚。首先，我给大家演示了圆锥体的生成过程。圆锥体虽然也有底圆和高度，但它是由三角形旋转生成的，而圆柱体是由圆拉伸而成。从它们二者的生成方式就可以看出，体积存在一定的差异。学生掌握了圆柱体的体积计算公式后，我让他们推理圆锥体的体积计算公式。假设和该圆锥体底面半径相同的圆柱体的体积计算公式为V ＝S×h，其中S 为底圆面积，可以由已知的底圆半径计算得出。学生很快就发现圆锥体的体积比圆柱体要小，部分学生推理出圆锥体的体积是相同底圆和高度的圆柱体的1/2 或1/3。面对几种不同的推理结果，在学生不知道准确答案或者对准确答案存在疑问的时候，我精心组织了一次推理验证实验。

在推理验证环节，我准备了一个圆筒和一个锥形容器，它们的底圆半径和高度一致，分别模拟推理题中的圆柱体和圆锥体，圆筒和圆锥里面一开始都是空的，没有水。接下来，我让学生先把圆锥形容器里面装满水，再把圆锥形容器里的水倒入圆筒中，学生发现虽然底圆半径和高度一样，但是，圆锥形容器里的水只填满了圆筒的一小部分，这说明相同底圆和高度的圆锥的体积远小于圆柱体积。但此时也无法确定倒入的水占到圆柱体体积的多少比例。接着，我让学生又一次将圆锥体容器盛满水并倒入圆筒中，学生们发现圆筒里的水还是不满。很显然，圆锥体的体积比圆柱体体积的一半要小，究竟是不是1/3 呢？我让学生再次将圆锥体容器盛满水，并再一次将水倒入圆筒中，这次正好把圆筒注满了。学生一下就明白了圆锥体体积是相同规格的圆柱体的1/3，对这两种几何体体积的关系认知也更加深刻了。一开始还有部分同学觉得圆锥体的形状比较奇特，很难准确得出它的体积公式，经过这次验证试验，彻底打消了他们心中的疑虑。我告诉学生，圆锥体是一类很常见的几何体，在以后的中学学习中会经常遇到。许多比它更加复杂的几何体都能够得到准确的体积公式。但是，需要大家掌握更加复杂的数学知识。验证环节也进一步强化了学生的严谨学风，在丰富学生数学知识的同时还提升了其学习兴趣，可谓是一举多得。同时，验证环节的开展也让学生知道了数学知识的具体应用策略。

三、肯定推理过程，保持推理兴趣

小学阶段的推理训练中，推理积极性和兴趣的培养往往比得到正确的推理结果更为重要。在推理圆锥体体积这一课上，经过试验验证得到圆锥体体积是同等规格的圆柱体体积的1/3 后，学生很开心，预测圆锥体体积是圆柱体体积的1/3 的同学更带有明显的成就感。我让学生把书本翻到圆锥体这一课，再次确认了圆锥体的体积计算公式。我表扬了成功推理出体积公式的学生；对于预测失败的同学，我也给予了鼓励，告诉他们，小学阶段还不能科学严谨地推导圆锥体的计算公式，推理出现错误是非常正常的事情［6］。许许多多的大科学家在探索未知科学问题时，一样会出错，包括著名的科学家牛顿。小学阶段的推理不是强调结果，更加重要的是鼓励和保护学生热爱推理活动的兴趣和积极性。一次次推理失败，并不能说明什么问题。相反，推理活动的兴趣和经验认知会逐步提升。

［案例4］拼正方体

在学习了正方体的体积计算公式后，我给学生提了一个问题：几个相同的小正方体能够拼成一个大的正方体吗？这个问题是我从小学生经常玩的魔方游戏和积木游戏中想到的。这个题目中，学生在推理过程中思维完全是开放式的，我并没有告诉学生小正方体有多大。有学生假设小正方体的边长为1，大正方体的边长为2，通过计算正方体的体积，得出8 个相同的小正方体才能拼出一个大正方体；有的小学生在脑海中展开联想，将小正方体的边长放大一倍，就能得到一个大正方体了。他们在脑海中算出放大后的正方体包括8 个小正方体。我充分肯定了这几种推理方式，这种推理说明小学生具备了一定的图形认知和联想能力。

总之，在推理训练环节中，教师要紧密结合小学生的知识能力水平，既要有一定的推理难度，又不能超出小学生能力水平，要融入数形结合思想，拓展小学生的数学思维；强化推理验证环节，加强学生对推理知识的认知和理解，强调过程和结果一样重要，保护学生的推理积极性。