三维视域下的概率犹豫模糊集及决策应用

朱国成，陈 煜，庄锡钊

(1.广东创新科技职业学院通识教育学院，广东 东莞 523960；2.郑州航空工业管理学院经济学院，河南 郑州 450018)

由于概率犹豫模糊集（Probabilistic Hesitant Fuzzy Sets, PHFS）能够很好地刻画决策群体对于事物的认知心理，在解决不确定信息条件下的多属性决策问题时非常实用.因此，自PHFS 的概念提出以来，该理论便在多属性群决策问题中取得了大量研究成果[1-5].然而，随着PHFS 在多属性群决策中的深入应用，其自身存在的局限性也渐渐凸显：虽然决策者给隶属度注解了发生的可能性即概率，但是发生以后的隶属度重要性则完全没有体现出来.例如，有5 位专家针对某个备选方案进行评价，有3 位专家给予7 分，1 位专家给予6 分，1 位专家给予5 分，此时对评价信息规范化并使用PHFS 进行描述，则可以表示为{0.7(0.6)，0.6(0.2)，0.5(0.2)}.事实上，在决策过程中针对评价专家的偏好经常发生，假如给予打7 分的每位评价专家权重为0.1，给予打6 分的评价专家权重为0.4，给予打5 分的评价专家权重为0.3，此时的PHFS 决策信息则可以表示为{0.7(0.6，0.3)，0.6(0.2，0.4)，0.5(0.2，0.3)}，由此可以直观看出各隶属度发生的可能性以及权威性.因此与经典的PHFS 相比，添加了决策专家权重的PHFS 显然蕴含了更加多元化的决策信息，在决策问题中更具实用价值.鉴于此，本文从三维视角下定义了PHFS，将隶属度、概率以及概率中所关联的决策专家权重以三维点坐标形式进行书写，并在此基础上建立了计算概率犹豫模糊元的几何距离函数模型、离差程度函数模型以及两个概率犹豫模糊元的大小判别准则.

在解决概率犹豫模糊集多属性群决策问题的过程中，确定属性的权重是必不可少的一个环节.计算属性权重的常用方法有熵值法[6]、离差最大化法[7]、线性规划法[8]等，无论哪种方法都是基于各个方案在属性上的整体信息差异程度而对属性权重的重新分配.目前，从方案在属性上的整体信息差异与属性内部评价信息差异两方面因素出发来计算属性权重的研究文献相对较少，因此，本文从此方面进行了研究.在决策算法方面，经典的方法是按照某种逻辑范式对方案的各个加权属性值进行糅合以获取方案的综合值，通过对比所有方案的综合值大小来达到排序备选方案的目的.据此思想，本文的算法1 利用Maclaurin 对称平均算子来集结各个方案的加权属性值，由Maclaurin 对称平均算子性质可知，集结结果大者对应的方案为优，案例分析进一步表明利用该法能够快速取得对备选方案的排序结果.与经典的决策算法不同的是，赵萌等[9]从属性的角度出发，对所有备选方案进行两两比较，并以此计算出任意一个方案与其他方案进行比较的总体利权值与总体弊权值，再利用每个方案的总体利权值与总体弊权值来对方案排序.受此思想的启发，本文的算法2 也从属性的角度出发，在所有属性上对所有方案进行两两比较，通过比较任意两个方案的属性优胜个数来排序方案.最后通过一个具体算例验证了两种算法在解决多属性群决策问题中所具有的实用价值.

1 预备知识

对于定义1，为了兼顾概率犹豫模糊元中隶属度lγ对应的概率lp所关联的决策专家权重，同时将隶属度lγ、概率lp、决策专家权重lω看作三维变量，以三维点坐标形式进行书写，此时，三维视角下的概率犹豫模糊集定义如下（见定义2）.

定义2 记非空集合X，将二元组称为集合X上的概率犹豫模糊集，其中

在定义2 中，显然最小的概率犹豫模糊数为(0,0,0)，最大的概率犹豫模糊数为(1,1,1).通过对概率犹豫模糊集中添加隶属度对应的概率所关联的决策专家权重可知，此时隶属度不但拥有了发生的频次，而且还具有了发生的权威性，故与传统的概率犹豫模糊集相比，新定义的概率犹豫模糊集蕴含的决策信息更加全面.

定义3 根据定义2，概率犹豫模糊数lxh的模糊值计算方法定义为：

容易验证，贴近度越大，对应的概率犹豫模糊数(γl,pl,ωl)就越大.同时，由式（1）进一步可知，最终决定概率犹豫模糊数lxh的模糊值大小的为隶属度、概率以及隶属度对应的概率所关联的决策专家权重等三者之中的最小者.

定义4 根据定义2，概率犹豫模糊元h(p, )ω的几何距离计算方法定义为：

性质1 概率犹豫模糊元h(p,ω)的几何距离e(h(p,ω))取值范围为e(h(p,ω)) ∈ [0,1].

所以有：

即e=e(h(p)) ∈(0,1).

综上可得e(h(p)) ∈ [0,1].

定义5 根据定义2，概率犹豫模糊元h(p,ω)，其离差程度函数d=d(h(p,ω))的计算方法定义为：

当概率犹豫模糊数以三维点坐标形式书写后，概率犹豫模糊元之间的大小比较问题需要按照新的方法进行测度.本文根据定义4、定义5，对两个概率犹豫模糊元h1(p,ω)和h2(p,ω)的比较规则定义如下：

下面给出一个例子来说明比较规则有效性.

例1 令概率犹豫模糊元h1(p) = {(0.6,06),(0.7,0.4)}，h2(p) = {(0.6,0.7),(0.7,0.3)}，试比较二者大小，

解：按照文献[11]中的方法，可得二者的得分函数值分别为s(h1(p)) = 0.64和s(h2(p))=0.63，即知h1(p) ≻h2(p).

此时若考虑决策专家的权重，在概率犹豫模糊元中，决策专家的权重进行平均分配，则有h1(p,ω) = {(0.6,0.6,0.5),(0.7,0.4,0.5)}，h2(p,ω) = {(0.6,0.7,0.5),(0.7,0.3,0.5)}，由定义4 得e(h1(p,ω)) = 0.495 5，e(h2(p,ω)) = 0.448 7，即知h1(p,ω) ≻h2(p,ω).

若在概率犹豫模糊元h1(p,ω)和h2(p,ω)中，决策专家的权重不进行平均分配，此时不妨设h1(p,ω) = {(0.6,0.6,0.7),(0.7,0.4,0.3)}，h2(p,ω) = {(0.6,0.7,0.8),(0.7,0.3,0.2)}，由定义4 得e(h1(p,ω)) = 0.520 2，e(h2(p,ω)) = 0.523 9，即知h1(p,ω) ≺h2(p,ω).

由例1 可知，本文定义的针对两个概率犹豫模糊元的大小判别规则是有效的，同时进一步可知，在概率犹豫模糊元中没有考虑决策专家权重或者决策专家权重进行平均分配时，皆不影响两个概率犹豫模糊元的大小比较.但是，当决策专家的权重没有进行平均分配时，则对两个概率犹豫模糊元的大小比较影响明显.考虑到在实际决策问题中，针对专家权重的分配很难做到平均，故在概率犹豫模糊元中考虑决策专家的权重是很有必要的.

定义6 概率犹豫模糊元h(p, )ω的加权综合值计算方法定义为：

定义7 在多属性群决策问题中，决策专家集Z= {z1,z2, …,zλ, …,zT}，其权重ωzλ表示且已知，方案集A= {a1,a2, …,ai, …,aM}，属性集G= {g1,g2, …,gj,…,gN}，属性权重用符号ωgj表示且未知，决策专家组给予第i个方案的第j个属性的评价数据信息用概率犹豫模糊元hi j(p ij,ωij)表示（如果在某个属性上的数据信息只有隶属度及对该隶属度认可的专家人数，则利用文献[11]中的方法将属性信息转化为概率犹豫模糊元数据信息），概率犹豫模糊元hi j(p ij,ωij)定义为：

若没有特殊说明，下文的概率犹豫模糊集的形式皆为定义7 中所示.根据定义2—定义7 有如下延展定义.

定义8 在概率犹豫模糊集多属性群决策问题中，概率犹豫模糊数的模糊值计算方法为：

式（5）中，k= 1,2, …, #hij(pij,ωij)，i=1,2, …,M，j= 1,2, …,N.

定义9 在概率犹豫模糊集多属性群决策问题中，概率犹豫模糊元hi j(p ij,ωij)的值用区间数近似表示，表示方法定义为：

式（6）中，k,k′∈{ 1,2, …,#hij(p ij,ωij)}，i=1,2, …,M，j= 1,2, …,N.

定义10 在概率犹豫模糊集多属性群决策问题中，概率犹豫模糊元hi j(p ij,ωij)的几何距离模型为：

式（7）中，k= 1,2, …, #hij(pij,ωij)，i=1,2, …,M，j= 1,2, …,N.

定义11 在概率犹豫模糊集多属性群决策问题中，计算概率犹豫模糊元hi j(p ij,ωij)的离差程度模型为：

式（8）中，k,k′= 1,2, …,#hij(p ij,ωij)，i=1,2, …,M，j= 1,2, …,N.

定义12 在概率犹豫模糊集多属性群决策问题中，概率犹豫模糊元hi j(p ij,ωij)的加权综合值为：

若hi j(p ij,ωij)中的元素只有一个，则规定d(hij(pij,ωij)) =mii′n(d(hi′j(pi′j,ωi′j)))(i′≠i).

由定义12 可知，影响加权后的概率犹豫模糊元的大小的因素来自两个方面，分别是概率犹豫模糊元的几何距离与概率犹豫模糊元中的元素（概率犹豫模糊数）两两相互之间的离差程度值.容易验证，概率犹豫模糊元几何距离越大，概率犹豫模糊元中的概率犹豫模糊数两两相互之间的离差程度值越小，加权后的概率犹豫模糊元的值越大.

定义13 令ai(i= 1,2, …,n)为一组非负实数，且有r= 1,2, …,n.若

则称 MSM(r)为Maclaurin 对称平均（Maclaurin Symmetric Mean, MSM）算子，这里i1,i2, …,ir为遍历组合1,2, …,n数中的一切r元组，为二项式系数.

容易验证Maclaurin 对称平均算子具有下列性质：

2 主要方法与结果

2.1 属性权重计算方法

为了能更加科学全面地利用决策信息来计算属性权重，这里从各个方案在属性上的整体信息差异程度与方案在属性上的内部评价信息差异程度两方面出发来确定属性权重.根据定义7，本文将概率犹豫模糊元的几何距离与概率犹豫模糊数之间的离差程度值相结合，利用熵值法来计算属性权重，具体计算过程如下：

首先，定义第j个属性的熵sj如下：

这里

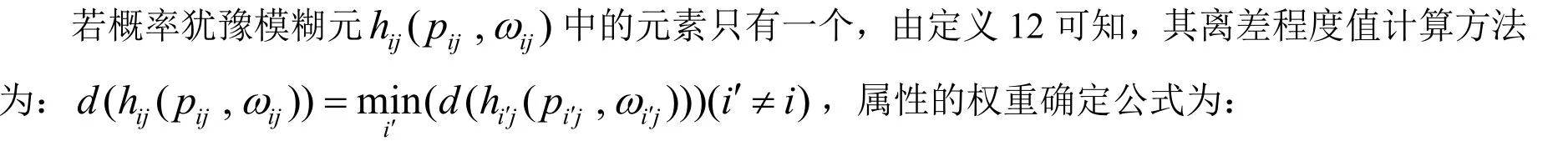
2.2 决策算法

在定义7 的基础上建立决策算法，具体决策步骤如下.

算法1.

步骤1：按照文献[11]中的方法，将决策专家给予方案的评分信息转换为概率犹豫模糊元决策矩阵HM×N=[hi j(p ij,ωij)]M×N.

步骤2：由2.1 节中的方法计算属性权重ωgj，j= 1,2, …,N.

步骤3：根据定义12 计算概率犹豫模糊元的加权综合值hi j(pij,ωij)ωg j=(pij,ωij).

步骤4：利用Maclaurin 对称平均算子对概率犹豫模糊元的加权综合值(p ij,ωij)进行集结，对第i个方案的集结结果用Hi表示，由Maclaurin 对称平均算子集结数据性质可知，Hi大者，其对应的方案ia为优.

算法2.

步骤1：按照文献[11]中的方法, 将决策专家给予方案的评分信息转换为概率犹豫模糊元决策矩阵HM×N=[hi j(p ij,ωij)]M×N.

步骤2：由2.1 节中的方法计算属性权重ωgj，j= 1,2, …,N.

由算法1 的计算过程可知，影响方案排序的因素有3 个，分别是概率犹豫模糊元的几何距离、属性权重以及属性权重在各个属性上的分配比例.从某种程度上说，算法1 中属性权重在各个属性上的分配比例对方案排序的影响程度最大，算法2 在对方案的排序过程中，影响因素只有一个，也就是概率犹豫模糊元的区间值，此时，属性权重在各个属性上的分配比例对方案排序没有影响.由此可知，两种算法的决策路径不同，决策过程中需重视的关键因素也不尽相同.

3 案例分析

例2 现实生活中经常会见到“男大未婚，女大未嫁”的现象，由于人们对物质条件的高质量需求及思想境界的“同频”要求，择偶期间男女双方更加看重对方的综合条件.以某父母的女儿择偶为例，女儿为某相亲平台会员，根据女儿对另一半的要求，平台给该家庭提供了3 位满足女儿要求的男士资料供选择并排序以方便平台尽快安排双方见面，家庭成员对3 位男士从8 个评价因素进行考察：财产、工作、家庭出身、健康、学历、才能、相貌、兴趣等，用g j(j= 1,2,…,8)表示，家庭4 位成员依次为：女儿、母亲、父亲及弟弟，用zλ(λ= 1,2,3,4)刻画，各位家庭成员参与对3 位男士评价，权重依次为ωz1= 0.6，ωz2= 0.25，ωz3= 0.10，ωz4= 0.05，被选择的3 位男士用符号ai(i= 1,2,3)表示，对3 位男士资料的讨论结果以家庭成员针对男士的某一个评价因素与女儿的匹配程度的数值形式给出（表1）.利用本文知识对3 位男士进行量化分析并排序.

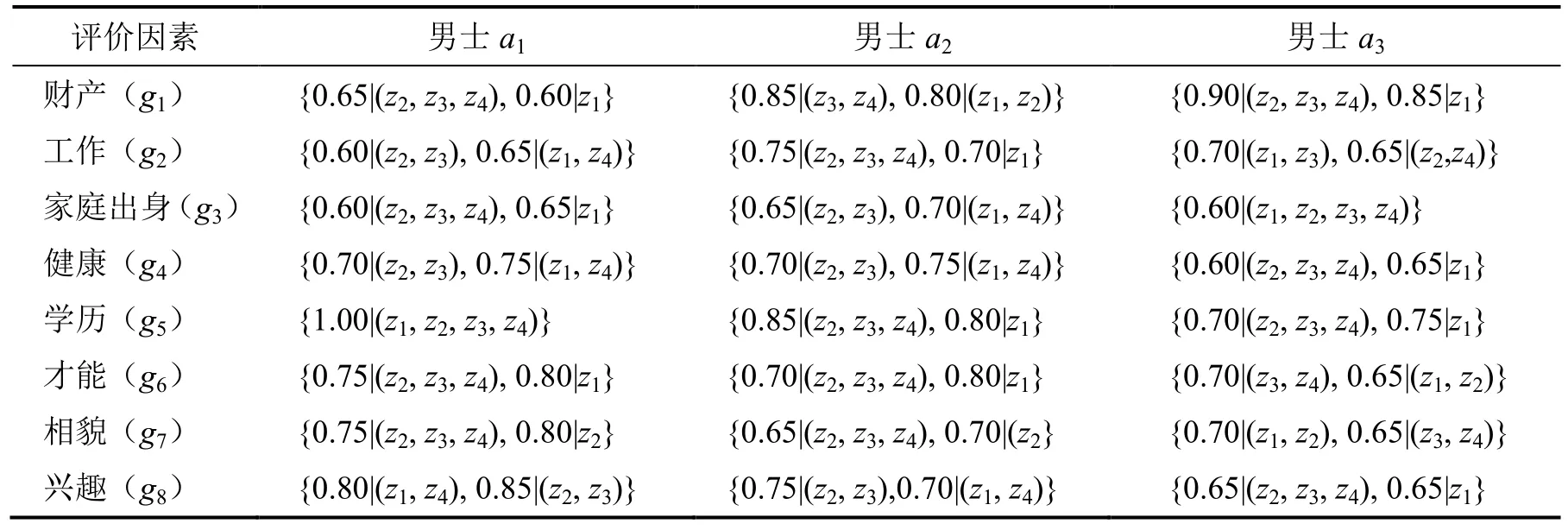
表1 家庭成员讨论评价表

3.1 算法1

步骤2：由2.1 节中的方法计算8 个评价因素权重（属性权重）ωgj，j= 1,2, …,8，分别得ωg1= 0.036 0，ωg2= 0.085 3，ωg3= 0.139 3，ωg4= 0.150 3，ωg5= 0.344 3，ωg6= 0.046 0，ωg7= 0.0433，ωg8= 0.155 3.这里 ∑8j=1ωgj= 0.999 8 ＜1，0.000 2 为计算时四舍五入方法造成的误差值.本文计算3 位男士的8 个评价因素权重不但考虑了概率犹豫模糊元的几何距离值，还兼顾了概率犹豫模糊元中的元素之间的离差程度值的问题，故，考虑的因素更加全面，计算方法有别于在概率犹豫模糊集多属性群决策问题中计算属性权重的普通做法，同时，该方法也丰富了属性权重的计算方法.

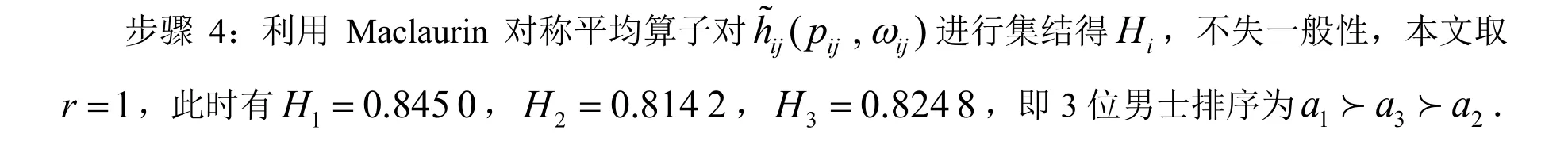
3.2 算法2

步骤1：前两步与算法1 一致，故可以直接进入步骤3 计算H ij(p ij,ωij).

步骤2：计算H ij(p ij,ωij)，i= 1,2,3，j= 1,2, …,8，依次可得

步骤3：利用定义14 对不同男士在相同的评价因素上进行测度并绘制测度表，如表2.由表2 可得，Q12=6 ，Q13=6 ，Q23=5 ，由算法2 排序准则得3 位男士排序为

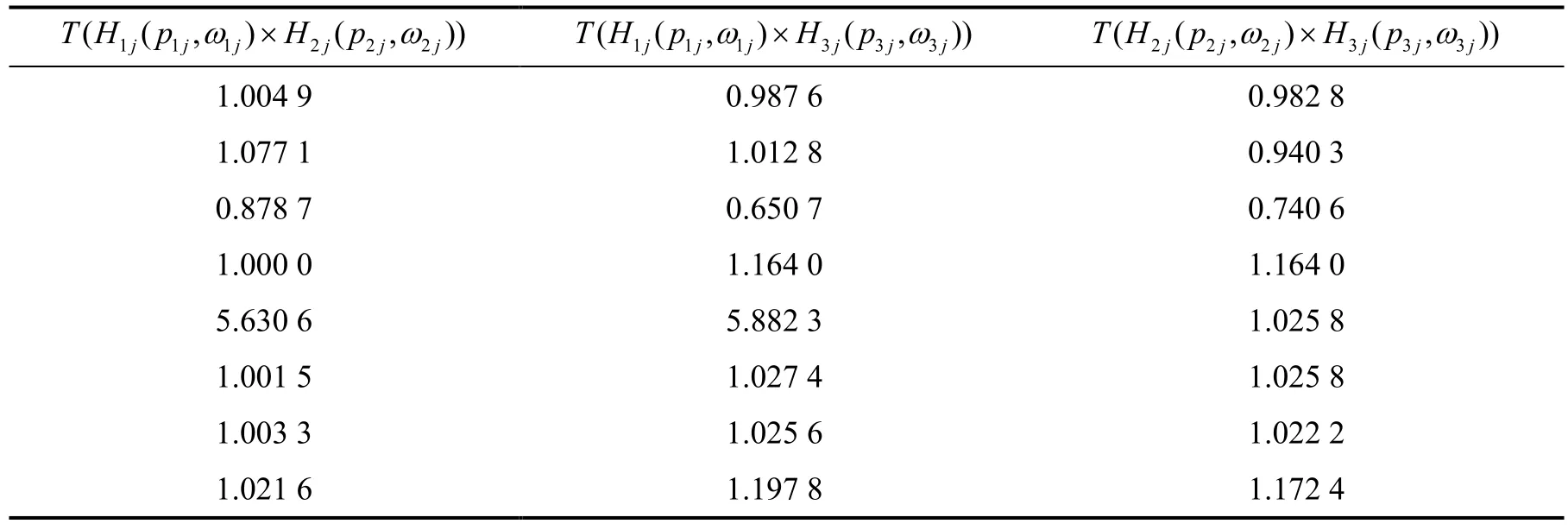
表2 测度表

算法1、算法2 在对3 位男士排序过程中都充分考虑了女方家庭4 位成员的重要性（权重），因此保证了决策过程中评价信息的严谨性，故两种算法的排序结果都具有重要参考价值.算法1根据4 位家庭成员对3 位男士在8 个评价因素上的评分值与在8 个评价因素的内部评分差异值来获取对3 位男士的综合评分值.算法2 在4 位家庭成员对3 位男士在8 个评价因素上的评分值的基础上对每位男士的评价因素进行两两比较，通过统计评价因素的优良个数来对3 位男士排序.两种算法的决策路径不同，则影响3 位男士排序的因素也不同，这也是导致第2 位与第3 位男士排序不同的根本原因，但都认同第1 位男士最合适，说明两种算法在汇总4 位家庭成员评价信息时对最适合的男士是保持一致的，进而说明了本文建立的两种算法的可行性.

4 结 论

本文在三维视域下定义了考虑决策专家权重的概率犹豫模糊集，并在此基础上采用熵值法计算了属性权重，建立了解决概率犹豫模糊集多属性群决策问题的两种算法.研究表明，两种算法都能快速取得排序结果，决策过程中两种算法都兼顾了每位决策者的重要性程度且在对最优方案的认同上一致.算法1 强调的是方案的综合条件，利用比较各个方案综合属性值的大小来对方案进行排序，通过分析影响算法1 的3 个因素可知，决策过程中考虑的影响因素比较全面，此方法具有普适性.算法2 通过比较不同方案的属性优良个数来对比方案优劣，由于影响算法2 的因素只有属性值的大小，与属性权重几乎没有关系，因此可知算法2 的决策路径具有一定的局限性.同时，假如方案的属性中具有一票否决式属性存在，则需慎重使用算法2（例如，在优秀教师评比当中，师德这一属性就是一票否决式，若在评比前，所有教师的师德都是无异议的，则可以使用该算法）.今后，我们将针对三维视域下的概率犹豫模糊集多属性群决策问题进行进一步研究，与传统的概率犹豫模糊集多属性群决策问题的解决方法作深入比较分析.