亨迪卡的条件概称句述评

董高伟

(中国药科大学 马克思主义学院, 江苏 南京 211198)

概称句(Generic sentences)又称为特征句,指不表示明确情节或独立事实,而是表达一类一般性质的命题[1]。关于概称句的研究开始于20世纪70年代。目前,国内学界对概称句的探讨[2]主要集中在SP型概称句上(1)参见文献[2],周北海指出,主谓结构的概称句,如 “鸟会飞”,其中鸟是主项(或主语),记作S,“会飞”是谓项(或谓语),记作P,此类概称句通常又记作SP。,如周北海和毛诩的双正常语义对概称句的解释[3],张立英介绍的概率方法对概称句的解释[1],Robert van Rooij和Katrin Schulz的因果力语义学对概称句的解释等[4]。雅各·亨迪卡(Jaakko Hintikka)是博弈论语义学(Game-theoretical semantics)的最初提出者,他在运用博弈论语义学解释条件句时,提出了一类条件概称句。本文主要介绍亨迪卡对条件概称句的解释,并对其解释方案进行分析。

一、 条件概称句及其成因分析

在一个条件句中,如果句子后件中包含一个(单数)代词,并且这个代词指称前件中量词所管辖的名词,那么这个句子就是条件概称句。例如:

(1)如果每一个学生都考试及格了,那么他一定非常努力地学习。

(2)如果张三有一辆自行车并且李四有一辆自行车,那么它在车棚里。

(3)如果比尔拥有一头驴子,那么他鞭打它。

在条件概称句中,前件所包含的量词等效于概称词,亨迪卡称之为概称量词(Geneirc Quantifiers)。在亨迪卡看来,条件概称句与SP型概称句的成因如出一辙,即在句子中包含了概称量词,例如:在SP型概称句“鸟会飞/A bird can fly”中,非限定词“(a(n))”即概称量词,具有概称属性。

条件概称句的结构特征是:句子后件中包含的代词指代前件中量词所管辖的名词,即句中的代词和它语法前件之间具有同一性。这不仅是条件句产生概称问题的关键,也是保证条件句符合语法的基本条件。亨迪卡所涉及的条件句中的概称问题,实质上是从存在量词到概称量词的一种转换,“无论什么时候存在量词只要构成了条件中的前件,就可以通过把它转换成概称量词,来适用于全部的条件”[5]。

从结构上考察条件概称句概称问题的成因,在于句子中后件所包含的代词没有指称前件中量词所管辖的名词,甚至指称不明。在日常语言中,由于这种不确定性,这样的条件句通常被认为存在语病。例如:

在例句(1)中,前件中的名词“学生”所指称的个体属于考试及格的学生的集合,后件中的代词“他”所指称的个体也应该属于考试及格的学生的集合,但是这样的句子给人的感觉是:言说者思维混乱,我们根本无法理解这样的句子是怎样的逻辑关系。造成这样的原因在于后件中代词指代前件中量词所管辖的名词这个条件没有得到满足,即在例句(1)中,“他”可以不指代“考试及格”的“任一个学生”,而是指代“一个不是学生却努力学习的人”,“他”和“任一考试及格的学生”两者之间并没有严格的互指关系。

在例句(2)中,句子前件包含了两个单个个体,后件中的单数代词“它”可以指定前件中的两个个体,而不是一个唯一个体,由此,代词“它”指称不明,代表的不是某个特殊个体。这即是例句(2)不可接受的原因。

在例句(3)中,后件中的代词“它”不是特指前面提到的某头特殊的驴子,因为我们无法从这句话中知道,“它”所指称的比尔拥有的这头驴子,与比尔拥有的其他驴子有何区别,也就是说,“它”即不是通常的名词函项(指出一个特殊个体的早期指称),也不充当所谓的指示代词(代表语法前件“驴子”)。

事实上,这类在日常语言中存在语病的条件句,症结就在于句中前件包含了的概称量词短语。在例句(1)中,“他”可以指代 “每一个考试及格的学生”中的任何一个,也可以不是;在例句(2)中,“它”既可以指代“张三的那辆自行车”,也可以指代“李四的那辆自行车”。例句(3)的意思等同于:

(4)如果比尔拥有每一头驴子,那么他鞭打它。

在例句(4)中的“每一(头)”是真正的概称量词。由此可见,在例句(3)中的“一(头)”具有“属”的功能,即它充当的是一个概称量词,而不是一个存在量词。不难看出,条件概称句后件中单数指示代词所指代的不是某个确定的个体,而是前件中概称量词短语的指称集合,本应表达非集合概念的量词短语实际上表达了集合概念,因此具有了概称属性。由此,亨迪卡得出结论:“条件句的前件所包含的存在量词,通常都属于概称量词。”[6]193

此外,在自然语言中,还有一些词具有概称意义,如“这个”“某个”等,例子如下:

(5)如果这头驴子是比尔拥有的,那么他鞭打它。

(6)如果比尔拥有某一头驴子,那么他鞭打它。

我们可以将例句(6)转换为例句(7),以便我们能更直接地看出“某个”所具有的概称意义:

(7)如果比尔拥有这头或那头驴子,那么他鞭打它。

从亨迪卡的博弈论语义学之视角,分析条件概称句概括称问题的成因,就在于用于刻画句子之博弈中的博弈策略缺乏必要的“粘性”。例如:运用语义博弈的方法处理例句(1)时,我们可以用“他”来代指“每一个考试及格的学生”的其中一个,化全称句为特称句,做出替换解释。但是,亨迪卡也解释道,这并不意味着“他”可以指称“每一个学生”,同时,“每一个学生”也能够指称“他”。因为在“自我”与“自然”的两人博弈中,“第一个也是唯一一个个体在与(1)相关的博弈中被自然选择出来,并试图证伪(1)的前件。……由于这些行动赖以建立的策略并没有‘记在’和条件后件相关的博弈中,因此不能支持后件中出现的代词。所以我们的理论预测,(1)中的代词没有发挥指代作用”[6]207。亨迪卡的意思是,在与(1)相关联的博弈中,自然的策略在前后件中并没有依赖关系,原因在于后件中的代词是“没有指称的指代”,由此,在自然的策略里,(1)中的“他”既可以指称一个自然任意挑选出的考试及格的学生,也可以不是。这种不确定性是博弈论语义学认为(1)不可接受的原因。

二、条件概称句的特点概述

较之于SP型概称句,条件概称句具有如下特点:

1.概称量词短语表达一个集合概念,具有“属”的功能。在例句(3)中,这个集合概念就是比尔所拥有的驴子的集合,而不是某头确定的驴子,我们不能认为比尔拥有的,仅只是他所鞭打的那一头驴子。概称量词短语所表达的集合概念通常可以适用于辖域内的个体,例如:我们通常可以这样来理解例句(3),即“比尔会鞭打这头驴,如果他拥有它”。这表明,在条件概称句中,概称量词和存在量词的区别是非常模糊的,在许多语境中,概称量词必须被当成真正的存在量词使用,反之亦然。

2.在条件概称句中,后件中的代词不一定严格对应前件中的名词所指称的某个特殊个体。尽管概称量词短语表达一个集合概念,但与全称量词所不同的是,概称量词所表达的是一个非全集,因此条件概称句中的前后件在语义上缺失必要的关联确定性。例如:我们不能由例句(3)推出例句(4),因为在语义层面,我们不能断定比尔鞭打的就是“他所拥有的‘这头’驴子”,理由是比尔也可能鞭打“他不拥有的‘那头’驴子”。这种不确定性是条件概称句的最重要的特点之一,也是对条件概称句进行语义解释的困难之所在。

3.条件概称句有真值。按照博弈论语义学,尽管参与人在不同语境对条件概称句的判断有所不同,但是他们都做出了判断,都对各自的取胜策略(断定条件概称句的真假)进行了选择,因此,条件概称句的前后件具有策略依赖关系,即条件概称句的前后件具有真值依存关系。如果否认条件概称句的真值,那么也就否认了博弈论语义学的立论基础。

4.对条件概称句所包含信息的整体理解必须是从物的。以例句(3)为例,如果仅是做出一个存在判断,即比尔拥有这头或者那头驴子,那么说比尔在鞭打它就变得毫无意义,因为这个时候我们的问题——比尔到底在鞭打什么?——没有任何答案。但是,对条件概称句前件的理解可以是从言的,在现实世界中,即使没有一个的实例符合条件概称句所表述的状态,条件概称句仍然可以为真。例如:即使比尔没有拥有驴子,例句(3)作为条件概称句仍然可能是真的。一方面,例句(3)可以看做是描述了一个未来的可能状态,是反事实条件句;另一方面,按照亨迪卡的观点,例句(3)后件中的代词并不一定指称驴子。

5.概称量词是在情境中考虑代词化行为的结果,对概称量词的界定与言说主体、语境等因素相关。在日常交流中,按照语用习惯,条件概称句一般被理解为特称句。例如:例句(3)往往会被理解为“如果比尔拥有某头驴子,那么他就鞭打这头驴子”。语用习惯属于交流主体的背景知识,是人们在长期言语交流中稳定沿用下来的语用规则的体现,其中包含了大量的心理因素,这也成为条件概称句在语义和语用上存在区别的主要原因之一,如何刻画这些因素,成为条件概称句形式化的难点。

三、博弈论语义学对条件概称句概称问题的消解

既然条件概称句后件包含一个代词,那么我们面临的主要问题就是:这个代词在前件中指称什么?亨迪卡说,条件概称句“对于语义的严重依赖表明了沿着纯语形的(生成的)路线对代词化进行描述是行不通的”[6]209。因此,与将重点放在前后件关系上的解释方法相比,博弈论语义学的解释方法是从语义出发,认为单数代词的前指使用,以假设了某个特别个体的出现为前提。亨迪卡指出,这种特殊个体并不能用只考虑前后件的语法关系来决定,而只能通过语义博弈过程中代词的实际指称情况来决定。要解决条件概称句的概称问题,首先需要考虑条件句的特征。

对于两人博弈G(Z),参与人为“自我”与“自然”,亨迪卡给出了博弈规则(G.if):

(G.if)当博弈形成如下形式的语句时,

(8)如果X,那么Y(If X,Y)

或者

Y,如果X(Y if X)

这是惯常对条件句的刻画,然而,亨迪卡对规则(G.if)并不满意。他认为,在日常语言的使用中,人们通常会做出相当纯粹的条件断定,也就是说,人们对条件句的关注点集中在后件,即Y的真假,而不是整句条件句的真假,换言之,除非认为前件X被确证或者被断定,否则对于条件句的断定就不会有分量。这与弗雷格的思想完全契合。在弗雷格看来,假的前提不能够推导出任何东西,只有真的思想才可以充当前提,并且这种真的思想是客观的,不是人们的假设。

亨迪卡就此指出,规则(G.if)并没有按照言说者语义推理一类形如(8)的条件句。在某种意义上说,我们推理(8)的过程应该是:首先通过推理X,然后看第一阶段的结果,再进一步推理Y,这样完成对(8)的推理。这一过程依照Karttunen的说法就是:处理条件句的有关理论要求人们先把条件句的前件增加到信仰储备的集合中去,这样如果能从新的信仰集合那里推出条件句的后件,就可以得出结论——整个条件句是真的[7]。按照这种思路,上面所提到的博弈规则(G.if)显然是不适用的,因为它太过于逻辑化了。

亨迪卡认为,既然博弈规则(G.if)是失效的,那么我们应该严格地从语义的角度来确认条件句(8)为真的条件,改善关于“if”的博弈规则。具体思路如下:对于两人博弈G(Z),参与人为“自我”与“自然”,关于X的不同确证方法,可以被看作是在相关的子博弈G(X)中自我可使用的不同策略,确证Y的努力是自我在子博弈G(Y)中可用的策略。那么对于博弈G(Z)最有用的理解,就是它是自我努力确证Z的尝试。自我对于(8)的辩护与自我在子博弈G(X)中的取胜策略相关。

要实现这个想法,亨迪卡认为最自然的方法就是让两个参与人首先开始子博弈G(X)。因为博弈论最重要的一部分就是选择策略,所以越到最后,越能看出一个人所采取的策略[8]。策略用函数表示。在博弈的后期,玩家的行动取决于在已经完成的子博弈中所采取的策略,因此参与人的后期策略是用高阶函数,而不是一阶函数表示,代表了对前一回合的策略的依赖关系。

然而,如果这样操作,亨迪卡就要面临一个难题,即自我在子博弈G(X)中的所有策略,在现实中很难且不需要全部实施。为了解决这一难题,亨迪卡提出可以通过类似于反证法的技术方式来处理,即两个参与人必须交换在子博弈G(X)中的角色。自然选择本来应当是自我的角色,反之,自我选择本来应当是自然的角色。如果自我赢得子博弈G(X),就会证伪X,且不用考虑Y,可以说此时自我是胜者。然而,如果自然胜出,就会证实X,因此自我必须考虑Y,两个参与人将继续进行子博弈G(Y)。

按照此种方法,自我在子博弈G(Y)中的策略取决于X被证实的方式,也就是说,取决于子博弈G(X)中自然对自我策略的选择。比较而言,自然并不享有任何特权,这次对局的结果将决定整个博弈G(if X,Y)的结果。由此,我们可以得到博弈规则(G.cond1),用图1表示出来[6]184。

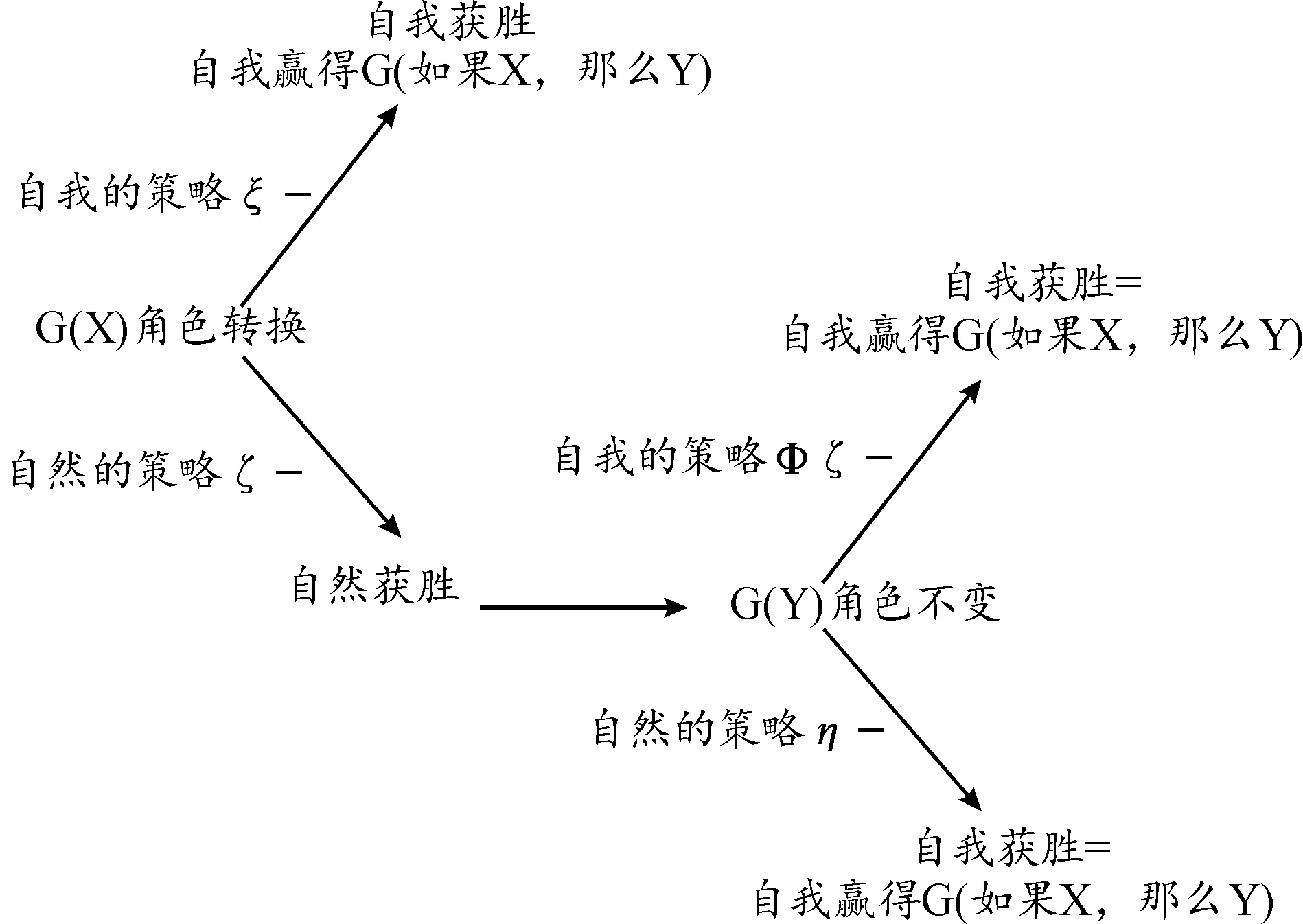
图1 博弈规则(G.cond1)流程图

根据图1,条件句的真可以定义为:“如果X,那么Y”为真,当且仅当有一个高阶函数Φ和一阶函数ξ,它们代表了自我的策略,并且它们能战胜用函数ζ和η代表的自然的任一策略。

两位参与人在博弈两阶段的关系如下:在子博弈G(X)中,互换了角色的自我和自然分别做出策略ξ和ζ,如果自我获胜,则博弈结束,如果自然获胜,则继续进行子博弈G(Y);在子博弈G(Y)中,自我做出策略Φ(ζ),并且策略Φ(ζ)取决于自然在子博弈G(X)中的策略ζ。而自然继续做出策略η,并且策略η取决于自我在子博弈G(X)中的策略ξ。相应地,在子博弈G(X)中,自我的取胜策略的映射,直觉上应该对应于在子博弈G(Y)中自我的取胜策略。

规则(G.cond1)是规则(G.if)的一个拓展,要解释条件概称句,“我们必须回到新规则(例如(G.cond)和(G.neg))的基础思想,这种思想就是,有时在某个情境中,一个词或一个短语的语义行为必须以合适的语义博弈方式进行,而当我们开始解释这些词或短语的意思时,这些合适的语义博弈就已经结束了。通常,这些关键词都是代词”[6]。也就是说,我们是按照从子句到子句的语序来理解一个句子,当我们看到一个给定的句子时,我们能够假定,先前与语句相关联的语义博弈已经结束。在亨迪卡看来,同一个文本中不同的语句通常被认为是合取的,并且先前的语句被认为是真的,因为只有当自我在早先博弈中胜出,参与人才会继续进行下一轮博弈。

亨迪卡强调,博弈规则(G.cond1)的要点不是给它所赖以建立的直觉思想增加更多的东西,而是指出η和ξ在G(Y)中是怎样充当我们关于条件的直觉思想的客观对象。

不难看出,亨迪卡解释条件概称句的基本思路是强调文本的上下文语境,认为在对一个条件句的前件的语词和语句理解的同时,已经确定了一个定义域,对整句条件句的理解必须是在这个定义域的范围之内的理解,从而排除了句子更多的语义歧义,缩小甚至确定了句子的语义范围。

以例句(3)为例子,亨迪卡指出,我们要明确例句(3)所描述的是关于被比尔打的所有驴子,或是关于没有被比尔打的驴子,或是关于比尔拥有的驴子。直觉上,一般的思路是:我们首先谈论所有驴子,然后将不是比尔的驴子排除,这样来进行量化。博弈论语义学对这一直觉过程刻画如下:(G.cond1)让玩家考虑自我在子博弈G(X)中的不同策略。虽然自我的策略并不指定个体(这些个体是自然选定的全称量化变量的值),但是只要使用这样的策略,就会在一次对局中产生某些个体,它们可以再次被代名词化地提起。而这样产生(特别挑选)的个体是存在量词提示自我挑选出来的。

具体操作过程如下:运用(G.cond1)到与(8)相关联的博弈中,自我必须将自我在G(X)中的每一个策略(称为ζ),与自我在G(Y)中的一个相似的策略相关联。在博弈中,这种关联是必须的,当且仅当ζ在子博弈G(X)中取胜。自我在例句(3)中的策略究竟如何?这里,X=“比尔拥有一头驴(Bill owns a donkey)”。理解“一(头)”最直接的办法就是把它看成是一个存在量词,可以得到例句(9):

(9)G(比尔拥有一头驴)

自我在例句(9)中的取胜策略,即是对比尔拥有的驴子的不同选择。因此在例句(3)的前件中,我们必须依次考虑比尔所拥有的驴子。这显然就是例句(3)的语义言说带给我们代词化的启示。当已经决定考虑例句(9)中自我的某个取胜策略之后,也就是说,考虑比尔拥有的一头驴子之后,我们就可以在例句(3)的后件中代名词化地提到每头驴子,并且能够确定是具体的哪一头驴子。这就是我们理解例句(3)的语义过程。这说明,自我的取胜策略就是在关于前件的子博弈G(X)中,自我给每头驴子指派一个个体,因此,当后件中的“它”需要我们去指认的时候,“它”已经有一个相关联的个体了。

值得一提的是,例句(3)中使得代词化成为可能的策略数量,和比尔拥有的驴子数量一样多。在直觉上,例句(3)中所选出的个体是自然在子博弈G(X)中做出选择后,引导自我们进行子博弈G(Y)的个体。准确地讲,是自我在例句(9)中所考虑的几个策略,引导自我去考虑在例句(3)的后件中哪个特定的动物可以用一个代词来指称,因为它代表了先前可以结束的子博弈的选择。

四、对博弈论语义学解释方案的评论

对于概称句,学界普遍认为是具有全称形式的特称句,并认为容忍反例是其最重要的特征。张立英[8]在《概称句的语义解释及形式化比较研究》一文中对SP型概称句的处理方法做出了总结,列举了相关限制、“不正常”限制、典型说、模态条件句方向和模态典型说5种处理方法。本文认为,这些处理方法同样适用于解释条件概称句。但需要指出的是,这5种处理方法在解释条件概称句时仍存在一些问题:首先,除模态条件句方向外,其余所列几类解释方法基本都是通过对前件名词所指称个体进行限制,从而解决条件概称句的相合性问题,然而这种限制如何确定并不明晰;其次,模态条件句方向会遇见情境选择的问题。

周北海提出了SP型概称句的双正常语义限制(1)参见文献[2],周北海指出,主谓结构的概称句SP都可以被精确化为“S(在正常情况下P)”。如果S是复数名词,则可进一步精确化为“(正常的S)(在正常情况下 P)”。以“鸟会飞” 为例,通过双正常语义限制,可以将不会飞的不正常的鸟,如断翅膀的鸟,被外层的全称量词略去;不正常的情况,如大气压力异常的环境,由内层的全称量词排除,从而保证了概称句“鸟会飞”语义解释的有效性。,沿着模态条件句方向处理了全称句与特称句的关系,这种解释是较为成功的。根据全称肯定命题与特称肯定命题的真假关系,前者为真则后者为真,后者为真则前者真假不定,当我们说“鸟会飞”为真,实指“那些(正常的)鸟(在正常情况下)会飞”为真,而后者为真不代表前者一定真,所以概称句能够出现反例。在日常交流中,人们使用了大量的概称句,但并没有引起理解上的困难,究其原因是在日常交流中,人们往往自觉地完成了全称句向特称句地转化。可以说,亨迪卡的解释方法更倾向于概称句的日常使用,刻画了多个认知主体间外在的语言交互活动[9]。

如前文所述,概称量词短语的本质语义与使用语义之间的差别产生了概称问题,因而对概称量词短语的使用语义加以限制不失为一个解决的方法。亨迪卡对于条件概称句的处理依然遵循主项限制的道路,但是与其他方法不同的是,在亨迪卡看来,这种限制不需要刻意进行,而是根据“进行原则”,诉诸人们的语用习惯和生活常识。

格赖斯(Grice)根据“修改了的奥卡姆剪刀”原则,即字面意义除非必要不作多义解释,把交际内容分为所言(What is said )和所含(What is implicated)。所言指字面意义,等于真值条件意义,而其他意义都放入所含(会话含义)中加以解释。前者属于语义学,而后者属于语用学,二者的界限是严格分明的。通过比较发现,亨迪卡的解释方法实质上是从语义学角度解释所含。在技术上,亨迪卡将概称量词短语的指称范围与策略行为联系起来,通过博弈规则的作用,将概称量词转化为存在量词,然后将存在量词的值与策略行为选择的个体相对应,从而达到限定概称量词短语的目的。

亨迪卡的成功之处在于较好地刻画了概称句的生成机制。理性人假设是博弈论的基本假设之一。人们在做称述时,“存在一个认知预设,即根据某一特征将要描述的对象从类的角度与其他事物区别开来”[10]。这个认知预设的基础,就是人们的知识背景。在对条件概称句的解释中,亨迪卡根据理性人假设自然地将前后件的关系对应起来,根据公共知识从心理选择层面对概称量词短语进行了限制。日常交流是在公共知识背景下进行的,换言之,日常交流是在一定的语境下进行的,因此亨迪卡将主项限制转变为对语境的限制,即在某个定义域D下,博弈能够顺利展开。依靠语境对公共知识集合做出调整,以便将概念的内涵和外延区分开来,并通过引入博弈论加强了其可操作性。

在亨迪卡看来,一方面,语境并不是空洞的存在,而是上下文的联系,可以通过策略选择的方式限制主项;另一方面,条件概称句作为一个整体也为理解句子提供语境。博弈论语义学是寻找和发现的游戏,所以在处理全称量词时,都将其化为存在量词来处理,如博弈规则(G.every)。按照这一方向,在处理概称量词的时候,也可以将其化为存在量词。这里,需要考虑两个集合:一个是满足条件的集合,另一个是例外的集合。我们只要关联句子的前后件,就可以确定概称量词短语的指称属于满足条件的集合,进而将例外直接排除。

综上所述,不难发现,亨迪卡的处理方法实质上是概称句的心理语义解释方案。亨迪卡将概称量词短语的解释归于参与人根据自身公共知识而做出的心理选择,实质上是将概称量词短语的解释转移到了如何形式刻画人们内心对于概念的指称选择上,这是一个颇有难度的问题,也是我们需要研究的课题之一。