计及边缘效应的平板电容传感器的输出特性*
王福谦 谭 浩 于学东 卿建东 张 玉
(四川西南航空职业学院机务学院 成都 610400)
1 引言
电容式传感器是一个具有可变参数的电容器。在现有文献[1~5]中,关于变面积型平板电容传感器的讨论,均未计及其极板的边缘效应,对由此带来的测量误差的研究也未见涉及。为此,本文拟将理论分析与计算机数值模拟相结合,利用保角变换法和格林函数法,研究变面积型平板电容传感器的电场和电容,以消除传感器极板所引起的横向边缘效应,得到精确度较高的电场和电容量的表达式,并利用软件Matlab绘制出该传感器电容量与动极板线位移之间的变化曲线,通过数值模拟分析影响该传感器输出特性的因素及不计极板边缘效应情形下减小测量误差的途径。
2 变面积型平板电容传感器的电场与电容
2.1 变面积型平板电容传感器的电场
变面积型平板电容传感器由间距为d的两相同平行极板组成,电势分别为U0和-U0,极板的长度和宽度分别为L和l,且L远大于l,上极板相对于下极板向右发生水平位移X,其横截面如图1所示。因在垂直于极板长度方向的所有截面上的电场分布都相同,则该传感器的静态场为平行平面场,故可取任一截面为z平面来讨论电势和场强在其上的分布,如图1所示。因为指数函数可将z平面上0 <Imz<d水平带域变换为ζ平面的上半平面,所以,为了利用格林函数法计算z平面上变面积型平板电容传感器内的电势和场强的分布,可作如下的保角变换[6]:
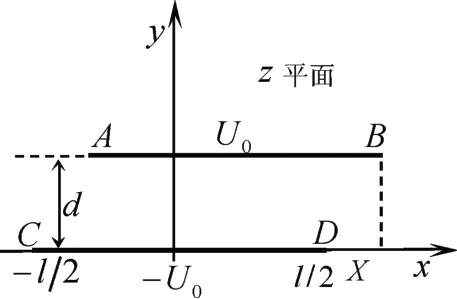
图1 变面积型平板电容传感器的横截面
经变换式(1),z平面上由两平行极板位置所限定的水平带形域0 <Imz<d,就映射为ζ平面的上半平面,变换后的ζ平面上两极板横截面的位置及其坐标可由式(2)确定,如图2所示。
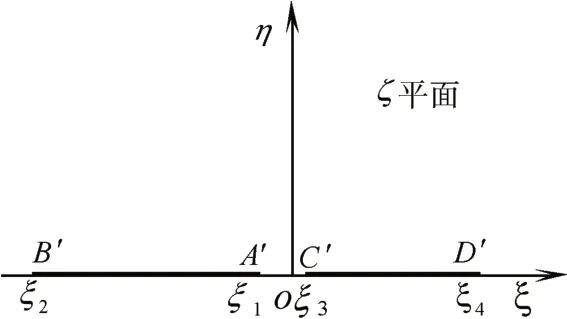
图2 变换后的上半平面及各极板端点的位置
经此变换后,z平面上的变面积型平板电容传感器内的电势分布就变换为ζ平面上的位于其上半平面的如下的边值问题:
对式(3)应用格林函数法[7~8],可得ζ平面上的电势分布为
由式(1),有
将式(5)中的ξ、η代入式(4),则得z平面上变面积型平板电容传感器内的电势分布为
由场强与电势的微分关系E=-∇φ,通过式(6)可得变面积型平板电容传感器内的场强分布为
为了给出变面积型平板电容传感器电场分布影响的直观图像,下面通过式(6),利用软件Matlab对其场分布进行数值模拟[9~10],绘制出了其横截面上的电场线和等势线(面)图(见图3)。图中的电场线与等势线及极板均垂直,场线分布正确合理,说明上述研究方法正确。
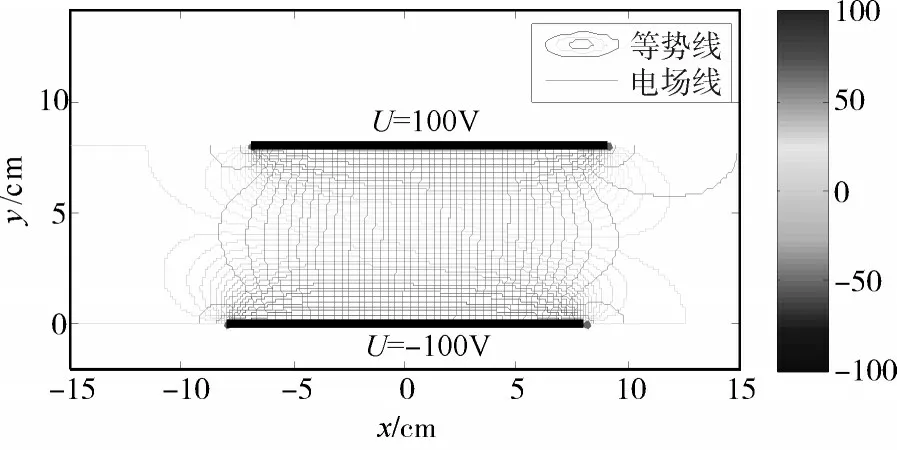
图3 变面积型平板电容传感器横截面上的电场(U0=100V,d=5cm,l=8cm,X=1cm)
2.2 变面积型平板电容传感器的电容
变面积型平板板电容传感器极板带电量的计算。为简便计,可设该传感器的两极板间的电压为U0(设上极板电势为U0,下极板电势为0),取式(6)中的y=y1=y2=0,可得其下极板上的感应电荷面密度的大小为
在下极板上对σ积分,变面积型平板板电容传感器极板的带电量为
由上式结合图1可得变面积型平板电容传感器的电容量为
因为该传感器内的场强分布是通过格林函数法得到的,且已计及了传感器极板横向的边缘效应,所以式(10)具有较高的精确度。
3 变面积型平板电容传感器的输出特性
下面利用Matlab[11~12]软件的数值模拟功能,通过式(10)绘制出变面积型平板电容传感器输出特性曲线,见图4。
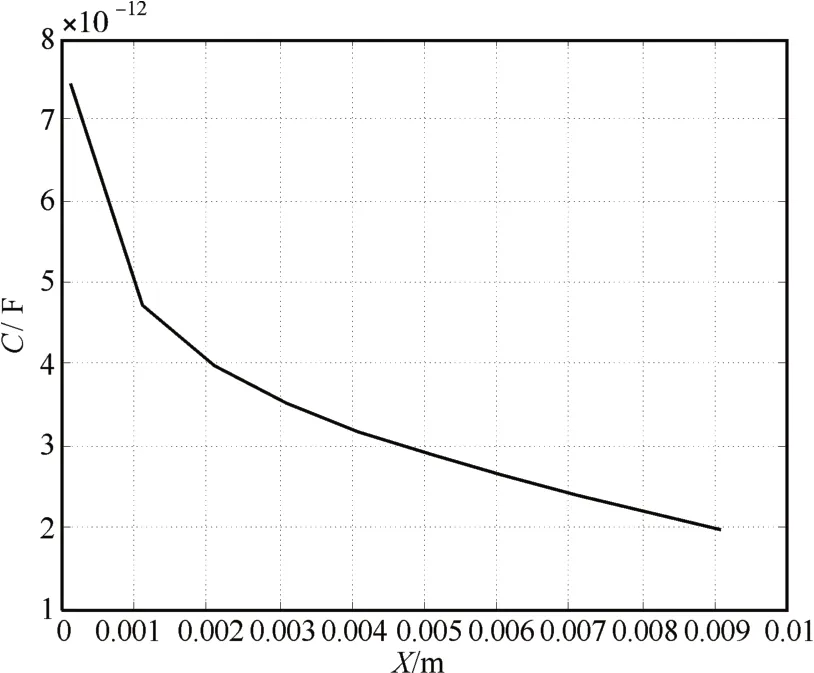
图4 变面积型平板电容传感器输出特性曲线(d=0.01m,l=0.02m,L=0.2m,εr=1)
3.1 变面积型平板电容传感器的输出特性分析
3.1.1 输出特性与d的关系
Matlab 软件的数值模拟结果表明:当该传感器的l和L保持不变时,减小极板间距d的数值,可提高其线性度和平均灵敏度,输出特性得到改善(见图5)。
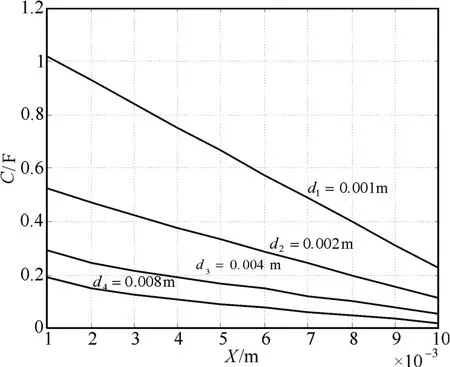
图5 变面积型平板电容传感器输出特性曲线(l=0.0125m,L=0.1m,εr=1)
3.1.2 输出特性与l的关系
Matlab 软件的数值模拟结果表明:当该传感器的d和L保持不变时,增大极板宽度l的数值,除该传感器初始电容量增加之外,其线性度和灵敏度几乎不变,输出特性没有明显改变(见图6)。
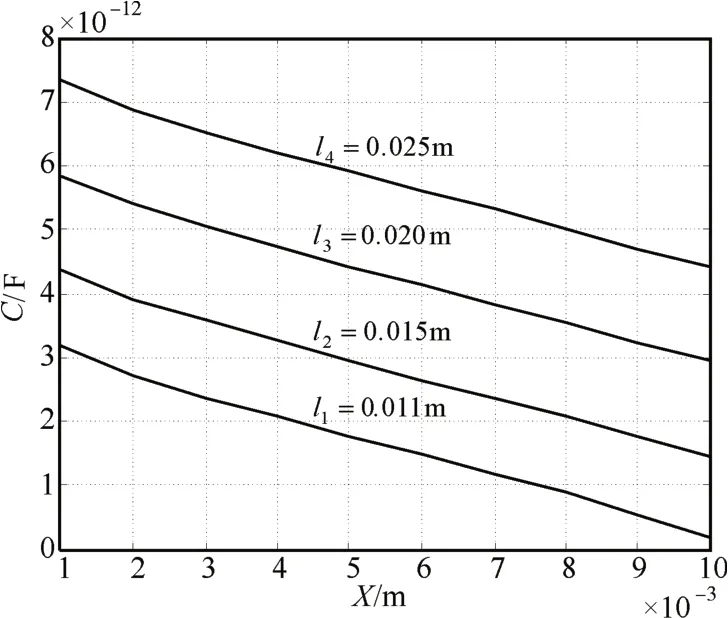
图6 变面积型平板板电容传感器输出特性曲线(d=0.003m,L=0.1m,εr=1)
3.2 改善输出特性的途径
从以上数值模拟结果(图5、6)可以看出,改善变面积型平板电容传感器输出特性的主要途径是尽可能减小极板间距;而增大极板宽度,对传感器输出特性的影响不大。
4 不计边缘效应的变面积型平板电容传感器的误差分析
在不计边缘效应时,变面积型平板电容传感器的上极板发生水平位移X,其电容量为
与式(10)比较可得变面积型平板电容传感器在不计边缘效应时引起的测量误差为
利用Matlab[13~14]软件,对式(10)和式(11),可绘制出变面积型平板电容传感器,在计及和不计及边缘效应两种情况下的输出特性曲线,其中实线曲线为计及边缘效应时该传感器的输出特性曲线,点线曲线为不计边缘效应时该传感器的输出特性曲线。由模拟结果可以看出,在极板宽度距l和测量范围(0.015m)一定的情况下,极板的间距d越小,测量的误差越小,见图7(a)和(b);在测量范围(0.015m)一定的情况下,极板的宽度l越大,极板宽间距d越小,测量的误差越小,见图7(b)、(c)。在d很小和l足够大时,两者的误差在一定测量范围内可以忽略,见图7(d)。所以,减小测量误差的有效方法是适度增大极板的宽度l和适度减小极板的宽度间距d。
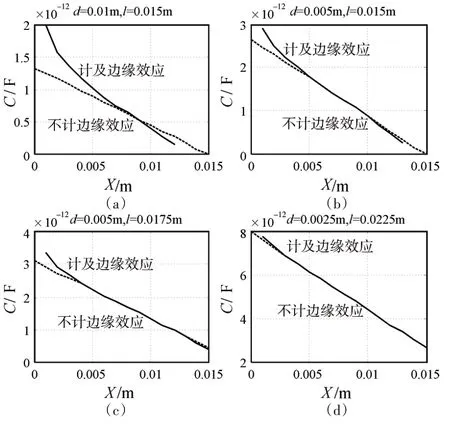
图7 不计与计及边缘效应的变面积型平板电容传感器的输出特性曲线比较 (εr=1,L=0.1m)
5 结语
计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第三种研究手段。本文将理论分析与计算机数值模拟相结合,研究了计及边缘效应的变面积型平板电容传感器的输出特性,指出了改善该容传感器输出特性的途径,并对不计边缘效应的平板电容传感器的测量误差进行了分析,给出了减小测量误差的方法。本文的研究的研究结论,对于提高变面积型平板电容传感器的测量精度具有一定的理论意义和实用价值,也可供相关问题的研究参考。

