基于多传感器组合导航系统的自适应算法研究*

侯 琪 李 沅 李 皓 王 丰

（中北大学信息与通信工程学院 太原 030051）

1 引言

惯性导航系统（Inertial Navigation System，INS）是一种定位定向导航设备，为载体自主、实时提供姿态、速度和位置信息［1］，具有不受地理限制、干扰小、结构简单等优点。其本质上是一个数值积分系统［2～3］，在实际应用中，由于器件的各种噪声以及计算上的误差会随着时间的增加而不断累积并发散［4］。捷联惯性导航系统（Strap-down Inertial Navigation System，SINS）因省去机电式的导航平台，使得整个系统体积、重量以及成本大大降低，但同时其动态误差要比平台式系统动态误差大，因此在长时间内很难独立使用。全球定位系统（Global Positioning System，GPS）作为非自主导航系统，具长期稳定定位、量测智能化等特点，但易受到外部环境因素的干扰导致可靠性下降。随着偏振技术的发展，天空偏振光作为仿生自主导航的重要分支，具有抗干扰能力强的优势［5～6］。多源组合导航可以充分利用单一导航的优势，提高导航的容错性与鲁棒性，增加观测冗余度［7］。

对于组合导航系统，滤波算法是影响导航性能的主要因素，工程上基本采用Kalman 滤波（KF）算法进行组合导航数据融合。模型统计噪声级在滤波过程之前给出，整个递推过程中保持不变，实际中众多因素会使得这种先验信息不再足以表示真实的统计噪声水平，不准确的状态估计量反馈至导航系统后会造成滤波发散问题。针对噪声统计特性的不准确问题，通常采用自适应卡尔曼滤波算法［8］。自适应滤波算法包括衰减记忆滤波、Sage-Husa 自适应滤波等方法，其本质都是通过不同参数调节噪声方差阵进行自适应估计，使其不断地适应系统的变化［9］。但衰减记忆滤波只能在一定程度上修正模型误差引起的系统噪声［10］。Sage-Husa自适应滤波的噪声协方差矩阵在多维系统中易失去非负定性并导致滤波发散［11］。

针对上述问题，本文提出了一种基于SINS/偏振光/GPS 组合导航自适应滤波算法，来解决子系统噪声方差阵异常或系统动态模型不准确情况导致的滤波发散问题。

2 多源组合导航滤波模型

2.1 系统方程

组合导航系统的误差状态向量均定义为SINS误差，包含9 个SINS 的基本导航参数误差和6 个惯导仪表的误差状态量，因此组合导航系统的状态向量可表示为

其中，δL、δλ、δh表示经、纬、高度的误差；δV表示东北天方向三维速度误差；ϕ表示东北天方向的航向姿态角误差；ε为随机漂移，∇表示加速度计零偏。

2.2 量测方程

SINS/偏振光/GPS 组合导航系统［6］量测方程中ZP、Zl分别为偏振光、惯性导航系统的观测矩阵，HP、Hl分别为偏振光、惯性导航系统的状态转移矩阵，如下：

1）GPS系统量测模型

将捷联惯导系统与GPS 之间的位置差Zl作为系统的位置量测信息。位置量测方程中Zl、Hl和Xl分别为

2）偏振光导航系统量测模型

将系统解算的航向角φs与偏振光导航解算出的航向角φp之差Δφ作为航向角的观测量，当姿态角误差为小角度时，航向角误差与平台误差角的关系为

其中，θs是导航系统解算出来的俯仰角。偏振光量测模型中Zp、Hp和Xp分别为

3 自适应卡尔曼滤波参数调整

3.1 量测噪声方差阵R估计

GPS 信号易受环境影响导致失锁［12］，偏振光辅助导航易受天气影响导致航向角信息误差增大，而SINS 短期内精度高。因此可利用这一互补优势对GPS 和偏振光系统量测噪声方差统计特性进行有效估计。

3.1.1 GPS量测噪声方差估计

设K 时刻GPS 和SINS 得到的同一轨迹的位置信息分别为ZGPS(k)和ZSINS1(k)，根据基于冗余量测噪声估计定理［9］，有：

其中，f(k)为量测系统误差，V(k)为动态噪声，且为零均值白噪声，ΔZSINS1(k)、ΔZGPS(k) 分别为SINS、GPS各自的一阶自差分序列。

因短时间内系统误差变化量很小，又惯导短时间内精度高，误差累计小，所以有：

其中RSINS1(k)、RGPS(k)分别为SINS 和GPS 测量噪声方差阵。

则GPS量测噪声方差估计可表示为

3.1.2 偏振光航向角噪声方差估计

设K 时刻SINS 计算得到的航向信息为ZSINS2(k)，偏振光探测系统解算得到的航向角信息作为姿态量测为Zlight(k)，有：

后续对偏振光导航系统航向角的方差估计计算与3.1.1 小节同理，得到偏振光航向角量测噪声方差估计为

3.2 修正系统噪声方差阵

通过3.1 节对R 的准确估计，该等式不成立则认为是由P(k，k-1)不准确引起的，P(k，k-1)对等式的影响程度可表示为

P(k，k-1)不准确主要受Q 影响且会呈现与Q相同的趋势，所以可通过αk实现对Q 的调整，间接实现对P(k，k-1)的调整：

其中，αk大于1 则表明系统噪声偏大，通过式（14）增大Q(k-1)，反之减小。

4 数据仿真与结果分析

4.1 仿真条件

本文利用轨迹发生器产生的仿真数据进行算法对比，其中SINS 采样频率为100Hz，偏振光和GPS 导航采样频率为1Hz；轨迹初始经纬度位置为112.444997°、38.016847°，高度为0m；初始速度为0m/s。设置陀螺仪零偏误差为0.3°/h；随机漂移为0.01°/h；加速度计零偏误差为100ug；仿真时长为2011s，生成轨迹如图1所示。

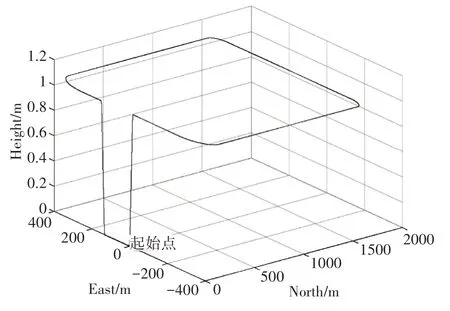
图1 运动轨迹

4.2 结果分析

为验证本文多源组合导航自适应算法的优势，在轨迹仿真1000s～1500s 内增大误差干扰，并且与扩展卡尔曼滤波（EKF）算法进行滤波对比，实验结果如下图所示。

如图2所示，航向角在整体滤波结果上有明显改善，在变噪时段滤波后均方根误差降低了55%。如图3、图4所示，在噪声非突变情况下，EKF 和本文改进自适应算法滤波的误差结果基本一致，但在1000s～1500s 的噪声突变情况下，通过图3、图4可以直观看出本文算法的优越性，表1可以看出该自适应算法较EKF 在经纬度均方根误差上分别降低了21.6%、25%。

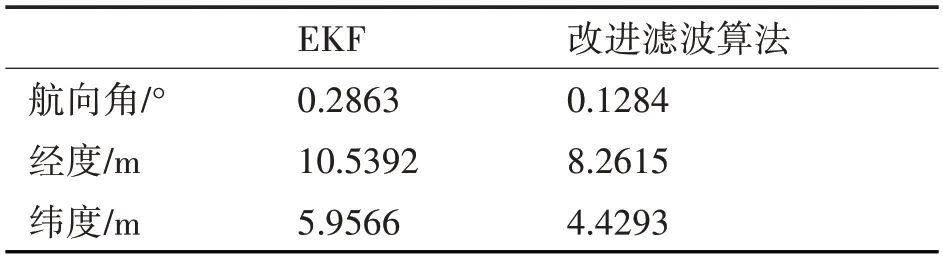
表1 变噪时段滤波结果均方根误差对比

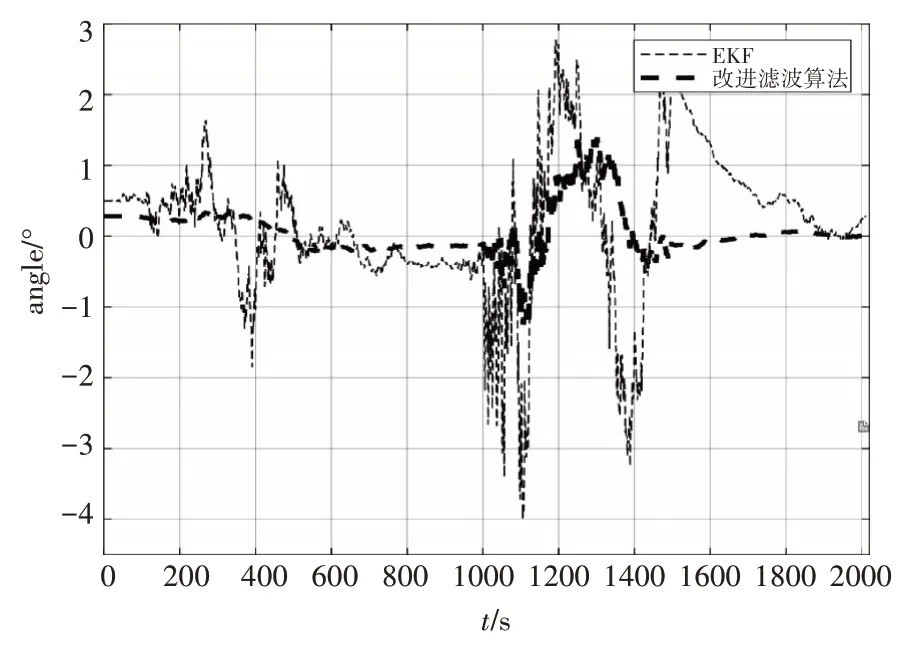
图2 航向角滤波误差对比

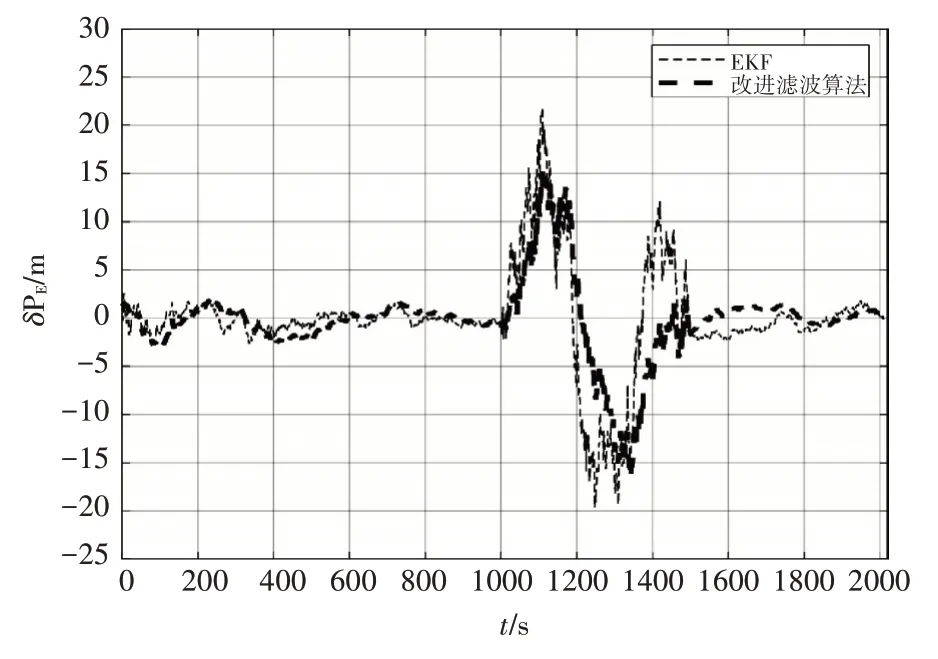
图3 经度滤波误差对比

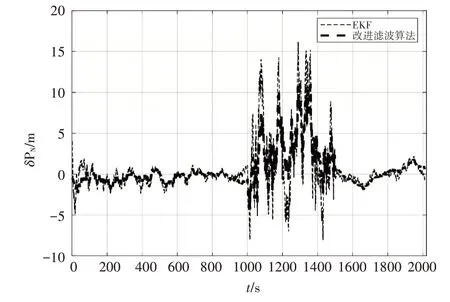
图4 纬度滤波误差对比

5 结语

针对GPS 和偏振光辅助导航系统出现干扰较大，量测噪声估计不准确以及系统动态模型不准确的情况，本文提出了一种基于组合导航自适应滤波调节方法。最终仿真实验表明该方法相比较EKF算法对姿态和位移有更好的修正作用，系统得到了有效的改善。