农业轮式机器人底盘转向运动控制及试验*

瞿济伟，李鸿基，张瑞宏，郭康权，丁钰洲，汪斌

(1. 扬州大学机械工程学院,江苏扬州,225000;2. 西北农林科技大学机械与电子工程学院,陕西咸阳,712100)

0 引言

我国设施农业综合机械化水平远低于全国作物耕种收综合机械化率[1],提高设施农业生产效率已成为亟待解决的问题,近年来农用轮式机器人的出现,促进了设施农业机械化水平的快速提升[2-3]。然而,传统轮式机器人依靠转向电机或复杂转向机构进行转向,其转向控制精度会对机器人行进路径造成影响[4],且温室具有密闭、狭小、障碍物多等特点,使农业轮式机器人的实际应用存在较大困难。

国内外农业轮式移动机器人转向控制研究广泛,Qiu等[5-9]设计的底盘,虽能实现原地回转、斜向行驶、横向行驶等多种运动模式,但都保留有转向电机,在转向时给各电机配合及控制增加了难度;王其东等[10-12]所开发的农用作业轮式机器人均采用差动转向方式,在平缓硬化路面上转向效果较好,但在松软土地上转向效果欠佳;Bakker等[13-16]中机器人转向部分采用液压驱动,底盘需装载液压系统,增大了机身体积与重量,不利于在温室等狭小空间中灵活作业。瞿济伟等[17]已经对此底盘的转向控制进行了大量探索,进行了转角跟踪控制研究和PWM波控制研究,取得了丰硕成果,但前期探索侧重于底盘静止状态转向控制和电磁锁控制精度研究,对轮毂电机控制参数的优化和行进中的转向协调控制研究还鲜有涉及。

针对以上存在问题,课题组提出基于轮毂电机驱动转向的农业轮式机器人底盘结构[18],极大简化了转向系统,为了实现灵活的转向运动及转向协调控制,本文提出了基于PID参数试验整定的转向控制方法,并进行了试验验证,以解决转向中各轮协调控制的问题,促进农业轮式机器人底盘的应用。

1 轮式机器人基本结构与控制系统

1.1 基本结构及转向原理

农业轮式机器人底盘(简称底盘)由机架、电磁摩擦锁、动力供电模块、中央控制器及转向机构等组成,如图1所示。底盘各转向轴上均设置有电磁摩擦锁,当底盘直线行驶或制动时,通过控制电路给电磁锁通以一定电流,电磁锁被锁紧,轮毂电机驱动轮不能相对于机架转动;当底盘转向时,通过控制电路减小电磁锁电流,电磁锁释放,驱动轮则相对底盘机架转动。

图1 机器人底盘整体结构简图

基于此特性,底盘可实现横行、斜行、原地回转等运动形式,如图2所示,能够在狭小、障碍物多的设施农业环境中高效灵活作业。

图2 底盘行走模式示意图

根据阿克曼转向原理,结合底盘自身结构特点,可得底盘前轮转向几何模型[19]如图3所示。转角α,β应满足式(1)。

图3 机器人底盘转向模型

(1)

式中:α——内转向轮转向角,(°);

β——外转向轮转向角,(°);

L——转向轴的纵向距离,mm;

K——转向轴的横向距离,mm。

转向过程各驱动轮的转向半径

(2)

(3)

(4)

(5)

式中:d——驱动电动轮偏置距离,mm;

Ri——第i个驱动轮的转向半径(以转向瞬心O为圆点),m,i=1,2,3,4。

以图3所示的左转为例,为了满足阿克曼转向几何,需对各个车轮速度进行精准控制,以2轮为主控轮,其余3个轮的速度以2轮的转速为基准进行控制(2轮转速系数为N),则剩余各个轮子的转速系数

(6)

1.2 控制系统

1.2.1 系统组成

轮式机器人主控制器采用单片机(STM32F103ZET6)采集4路转角信号、4路转速信号、1路模拟方向盘信号、1路模拟油门信号,输出4路占空比可调的PWM到轮毂电机控制器,控制轮毂电机转速,另外输出4路PWM信号控制电磁锁的开闭。基本控制原理如图4所示。控制系统主要由继电器控制的电磁锁部分、精密多圈电位器的油门信号和转向信号、单片机、传感器、线路、电源组成。为了使转向信号器转速可控,采用精密多圈电位器与步进电机固连的方式,使得转向信号器精确可调。转向控制器实物如图5所示。

图4 控制原理

图5 控制系统组成

系统工作时,单片机需要采集10路电压信号,包括4个驱动轮转速信号、转角信号、1路油门信号、1路方向盘信号,输出4路占空比可调的PWM波控制电机转速,另外输出4路PWM波信号控制电磁锁。STM32F103ZET6单片机外设ADC1采集4路转角和转速信号及方向盘和油门信号、DMA传输ADC采集的数据到内存中、基本定时器TIM6定时中断、高级定时器TIM1和TIM8输出PWM控制电机转速、普通定时器TIM2,3,4,5控制电磁锁开闭、串口USART1打印实时数据到电脑屏幕,用于调试。

1.2.2 控制策略

控制车轮转速主要包括位置式PID和增量式PID两种算法[20]。二者算法基本一致,区别在于位置式PID是对过去所有误差进行积分,输出PWM控制值;而增量式PID只是对过去三个误差进行积分,输出增减量。不同于步进电机,轮毂电机对位置不能自主累加,因此,只能选择位置式PID,通过对误差的不断累积,增大调节力度,从而对轮毂电机进行控制。在PID控制系统中,输出u(t)与输入e(t)之间的关系如式(7)所示。

(7)

式中:e(t)——偏差;

Kp——比例增益;

Ti——积分时间常数;

Td——微分时间常数。

对式(7)离散化处理后得到式(8)。

(8)

式中:T——采样周期;

u(k)——第k次采样时的输出;

e(k)——第k次采样时的偏差;

e(k-1)——第k-1次采样时的偏差。

由于每次输出值u(k)直接和执行机构的位置一一对应,故式(8)即代表位置型PID算法。

因底盘采用的轮毂电机为直流无刷电机,经前期反复调试,采用PI控制就能够发挥其启动转矩大、调速范围宽的优点[21]。因此,最终的PI控制算法表达式如式(9)所示。

(9)

另外,设定τ为限幅值,当u(k)的绝对值小于τ时,输出u(k);当u(k)的绝对值大于τ时,输出τ。需通过大量的试验对Kp和Ki进行整定,以获得有效可行的控制参数,其PI控制的程序流程如图6所示。电磁锁控制流程如图7所示,以目标角30 °为例,外轮转速大于内轮转速,由于油门信号和轮毂电机转速之间并非线性关系,同样油门信号情况下,加速和减速时轮毂电机转速的增量并不相同,为了满足式(6)推导的转速比,经过前期试验校准,需设置外轮转速为油门信号的1.2倍,内轮转速为油门信号的0.5倍。根据方向盘转角信号和2轮转角计算出具体转速系数后,分别对其他轮转速赋值,并判断转角关系是否满足,分别执行相应的电磁锁操作,完成转向过程。

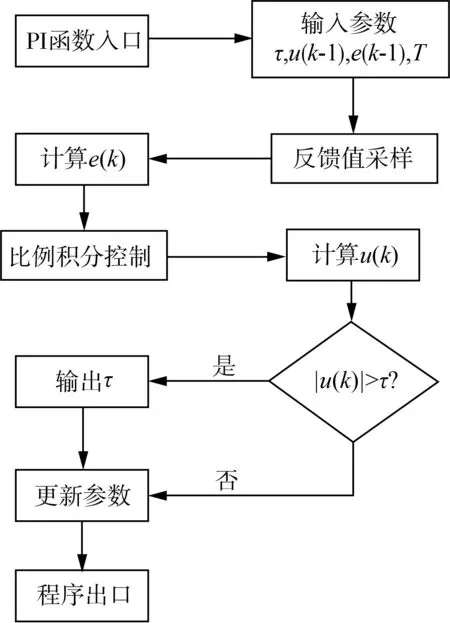
图6 轮毂电机PI控制流程

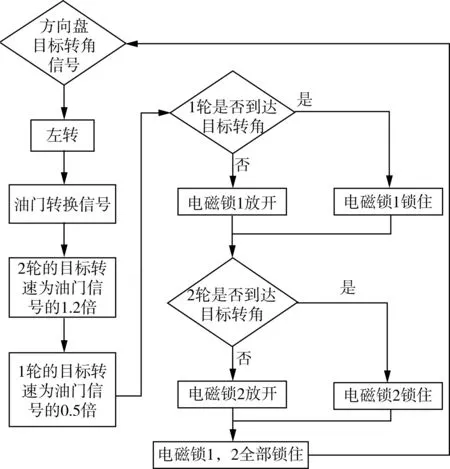
图7 电磁锁控制流程

2 转向控制参数整定

2.1 参数整定方法

参数整定试验设备如图8所示。包括笔记本电脑,单片机(STM32F103ZET6),数据采集卡(USB2852)采集数据,转速传感器(D046)采集悬空放置单轮转速,转角传感器(22HP-10精密多圈电位器)采集转向转角,电磁摩擦锁(FBD-050),轮毂电机(WX_WS4864)等。一般PID整定试验先从Kp进行整定,但是对于位置式离散PID,由其输出公式(9)可以看出,若无Ki,则系统输出将一直保持在较低水平,另外为了更快获得Kp、Ki的准确结果,采用先Kp后Ki的交替变化模式,开始时先确定一个Kp值和较小的Ki值,Kp和Ki以基数的倍数增加[22]。通过前期试验确定基本稳定的Kp与Ki的范围,即Kp=0.15～0.6,Ki=0.01～0.02。为得到更为精确的参数值,设计了如表1所示的6组试验,并分析整定过程。

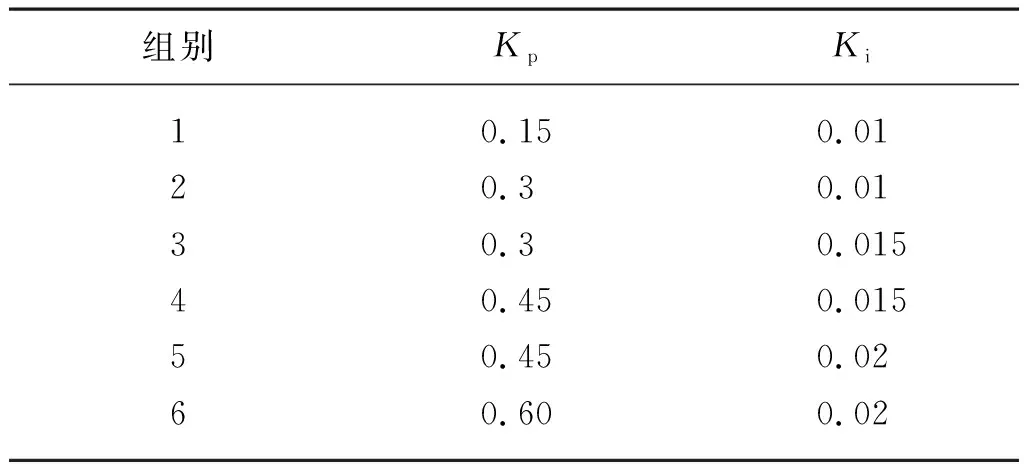
表1 PID整定试验方案Tab. 1 Test scheme of PID parameter tuning

图8 试验设备示意图

2.2 控制参数整定与获取

采用MatLab软件编写函数,用于求解延迟时间、上升时间、峰值时间、调节时间与超调量。鉴于轮毂电机转速范围较宽,对转速进行了40～90 r/min和90～130 r/min区间分组,分别进行加速测试,并采用Origin软件与Matlab进行单位阶跃响应分析。

2.2.1 40～90 r/min区间参数整定

Matlab求解函数的具体参数见表2。各个控制因素响应曲线以及实际转速的单位阶跃响应曲线分别如图9、图10所示。

表2 转速区间为40～90 r/min时计算系数表Tab. 2 Calculation coefficient table at speed range of 40-90 r/min

图9 实际转速与目标转速响应

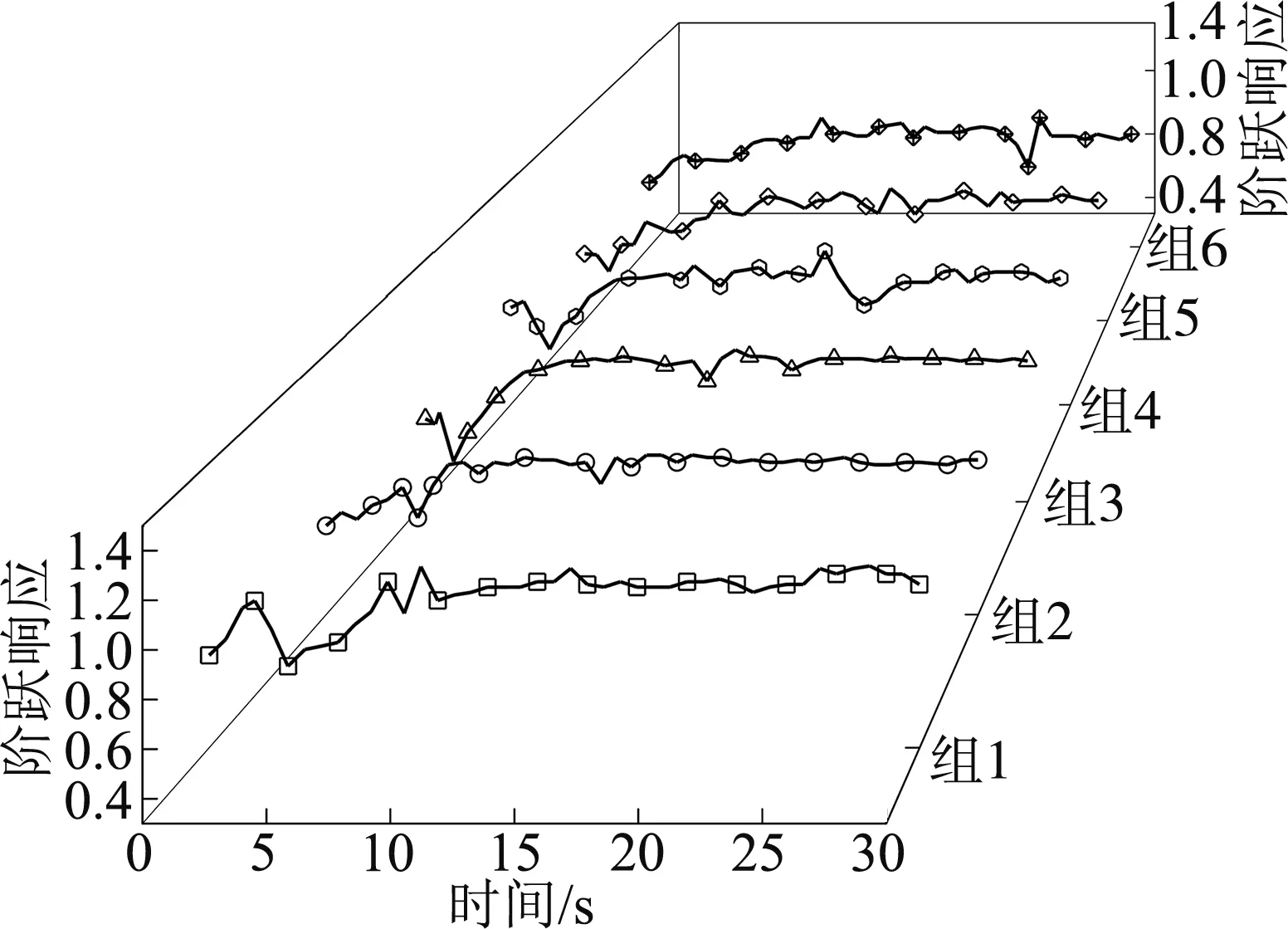
图10 单位阶跃响应

2.2.2 90～130 r/min区间参数整定

求解函数具体参数见表3。各个控制因素的响应曲线以及实际转速的单位阶跃响应曲线分别如图11、图12所示。

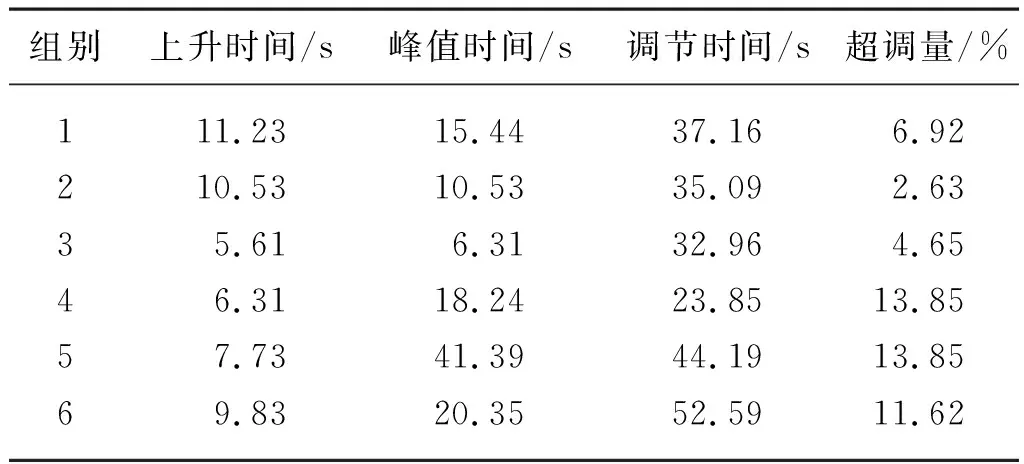
表3 转速区间为90～130 r/min时计算系数表Tab. 3 Calculation coefficient table at speed range of 90-130 r/min

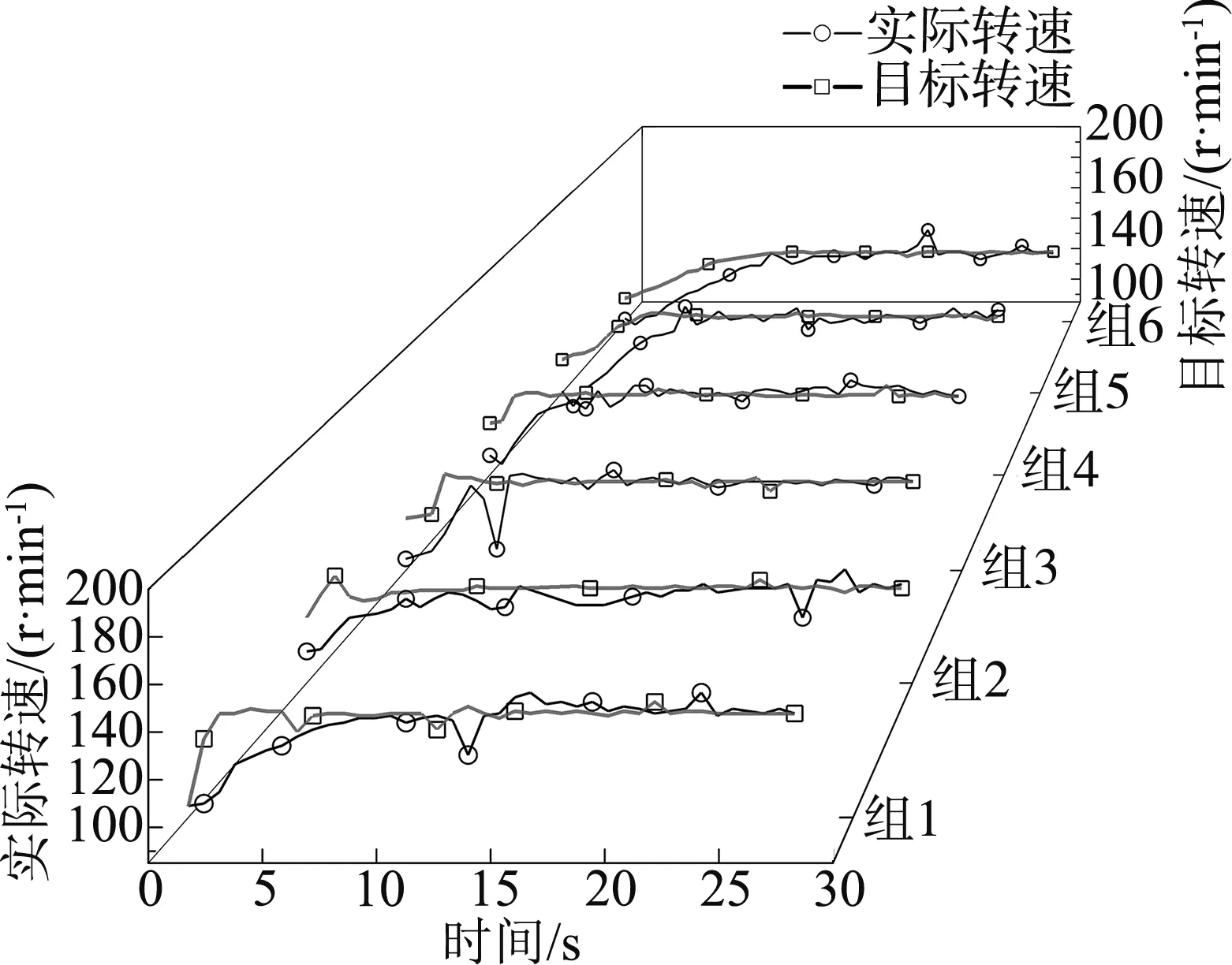
图11 实际转速与目标转速响应

图12 单位阶跃响应

由上述两组速度区间响应图可知:组1实际转速稳定在目标转速附近,控制的精准性已经达到低速作业柔性底盘的作业需求;组2在单纯增加Kp之后,上升时间减小,超调量减小;组3在增大了Ki之后,系统整体上升时间进一步减小,更加符合使用要求,但系统超调量也略微增加;组4与组5在进一步增大Kp之后,对上升时间影响不大,却增大了系统超调量,控制精准性也受到了轻微影响;组6在增大Kp之后,实际转速转速特性仍稳定在目标转速附近,但由阶跃响应曲线可得系统已经不稳定,因此不应该再增大Ki。在数据分析中也发现,转速传感器受轮胎抖动的影响,造成微小误差。

在多组试验基础上,对其中最为接近的6组数据进行了分析,可以看出积分Ki=0.02时,系统超调量已经很大,对于PI控制器不应再增加积分常量。Kp=0.45,Ki=0.02参数条件下,系统响应最符合使用要求,超调量较小,上升时间较快。

3 台架试验

3.1 试验设备

本文采用前期开发的试验台(图13)[23]进行试验。

图13 试验台与样机结构图

4个水平转盘与4个电动轮刚性连接,通过控制电路驱动轮毂电机在水平转盘上转动,每个水平转盘由4个橡胶轮支撑,其回转中心轴与底盘4个偏置转向轴轴线重合,可模拟底盘在路面上的转向行走状态并测试。

3.2 试验方法

3.2.1 因素与水平

轮毂电机转速:机器人底盘工作速度为0～3.6 m/s,则轮毂电机转速为0～120 r/min,取4种转速水平,分别为:30 r/min,60 r/min,90 r/min,120 r/min。

转向机构转角:理论上为-90°～+90°,而传统车辆车轮最大角度不超过40 °,故底盘前内轮转角取4种水平,分别为:10°,20°,30°,40°。

转向信号器转速:转向信号器用步进电机驱动转动,步进电机能实现6～110 r/min任意调速。

为了提升试验精准性,试验将转向信号器转速水平分为19～97 r/min;可以利用式(10)直接将转向信号器转速转化为实际输入单片机的转角信号。试验所用车轮转角信号对应关系如表4所示。

表4 内外轮转角对应关系Tab. 4 Angle relationship between internal wheel and external wheel

v=0.137v1

(10)

式中:v——实际输出角度信号,(°)/s;

v1——转向信号器转速,r/min。

3.2.2 评价指标

为了分析转向过程的转向符合情况,采用阿克曼率[24]来评定转向控制的平稳性。用内外轮实际转角差与理论转角差的比值r表示阿克曼率,%。

(11)

3.2.3 试验设计

首先进行小角度转向试验,计算伺服电机转动角度,确定方向盘转动速度。因素水平表如表5所示。

表5 因素水平表Tab. 5 Factor level table

每组试验重复5次取平均值,并利用Origin软件进行数据处理。

3.3 试验结果分析

本研究以外轮目标转角为30°、内轮目标转角39.15°时,转向信号器转速为45 r/min、电动轮转速为30 r/min以及转向信号器转速为71 r/min、电动轮转速为90 r/min的2组试验为例进行转向过程分析,并通过各轮转角响应与阿克曼率进行评价,响应曲线如图14、图15,阿克曼率曲线如图16、图17所示。

图14 转向信号器转速45 r/min、电动轮转速30 r/min的转角响应曲线

图15 转向信号器转速71 r/min、电动轮转速90 r/min的转角响应曲线

图16 转向信号器转速45 r/min、电动轮转速

由图14、图15可知,外轮目标转角为30°、内轮目标转角39.15°时,内外轮都存在1°～3°的转向误差,其中角度传感器的抖动,造成角度反馈不准,内轮误差较大;另外,转向趋势小,造成各轮转角不能及时跟随方向盘的信号,但验证了控制策略的可行性。由阿克曼率响应曲线可知,由于驱动力较小,车轮转向难以跟上方向盘给出的信号,因此在转向初期,阿克曼率较小,随着姿态的调整,逐渐符合最终的阿克曼转向几何关系。

阿克曼率不能够始终维持在100%附近,原因是转角采集传感器的偏差;另外,试验台水平转盘存在微小抖动,数据有一定波动,但在可接受范围内。以试验台中目标角为30°的中的两例进行了数据分析(图16、图17),用阿克曼率来评价转向过程,结果表明,还需进行硬化路面试验进一步验证。

4 路面试验

4.1 试验方法

将3.1节中所示样机在平坦硬化路面上进行测试,首先,检查程序,测试电磁锁是否能够在到目标角度后锁紧,设定转向信号器中伺服电机转动角度和转动速度;然后,转动油门模拟器所使用滑动变阻器,使车身以合适速度行进;最后,在到达转向区域时,启动转向信号器转向伺服电机,观察转向过程,保存试验数据。试验中底盘转向平稳,并且底盘可稳定进行大角度转向,基本能够实现原地转向,转弯半径大大减小。共进行了4组验证性试验,转向信号器转速为45 r/min、71 r/min,前外轮的转向角度为10°,20°,30°,40°。具体试验方案如表6所示。

表6 硬化路面试验方案Tab. 6 Test scheme for hardened road

4.2 数据分析

在机器人底盘实际作业过程中,运动模式以大角度转向和中低速行进为主,因此采用转角20°、转速71 r/min 和转角40°、转速45 r/min两种典型工况,即工况2与工况4,分析硬化路面行进中转向过程。各轮转角曲线如图18、图19所示。

图18 工况2转向过程

图19 工况4转向过程

分析两个工况可知,外轮(2轮)比内轮(1轮)的控制精度高,原因可能是外轮作为主控轮数据传输较快,以及外轮处于车辆外侧受到来自内侧的向外挤压力使得锁紧误差减小。因此,底盘内轮电磁锁锁紧力应大于外轮,以减少控制误差。曲线出现小范围波动是由于路面随机干扰,造成角度反馈不准;另外还有数据处理带来的舍入误差。通过对比两组数据可得,内外轮接收到目标转角指令后,能在3 s内到达目标角度,两轮状态能及时跟随目标角度进行调整;整个转向过程响应曲线斜率基本一致,说明内外轮能保持良好的阿克曼率;同时,减小转向信号器转速可以减小最终姿态控制误差,说明转向信号器转速低时数据传输更加稳定,与电磁锁响应时间更加契合,控制精度更高。随机误差与电磁锁响应时间和传感器采集误差有关,导致电磁锁锁紧时间迟后,影响控制精度;另外电磁锁安装存在1°～2°活动角度,影响转向精度。各轮最后实际角度与目标角度存在2°～3°偏差,在转向控制误差允许范围内,验证了控制策略的可行性。

5 结论

本文针对农业轮式机器人转向协调控制问题,提出了一种转向运动控制策略,通过试验得出结论如下。

1) 机器人底盘的PID参数整定试验表明,PI控制参数为Kp=0.45,Ki=0.02时,超调量较小,上升时间较快。

2) 试验台转向控制试验表明,机器人底盘前轮无法立即跟随方向盘进行转动,存在1°～3°的转向控制误差,但随着时间推移,各轮逐渐吻合阿克曼转向关系,验证了控制策略的可行性。

3) 路面试验表明,控制策略有效可行,最终控制偏差在2°～3°,转向过程时间在3 s以内,满足本机器人控制精度要求。但转向信号器转速不宜过快,否则会造成机器人转向误差增大。