基于响应面法的棉秆粉碎还田试验*

李明刚，杨会清

(滨州市农业技术推广中心,山东滨州,256600)

0 引言

棉花作为我国重要的经济作物、战略物资和纺织工业原料,2020年种植面积为3 169.9 khm2[1]。棉秆作为棉花种植的主要副产物,其综合利用不仅可以给农民带来可观的经济效益,还可以带来巨大的社会和生态效益[2-5]。目前,棉秆粉碎还田是最主要的利用方式。研究显示,棉秆中富含氮、磷、钾和微量元素,将棉秆作为秸秆肥进行粉碎后还田不仅可以减少化学肥料的使用,提高土壤有机质,改善土壤理化性质[6-7];还可以显著提高棉花总铃数、单铃重和产量,在一定程度上提高棉花品质[8-9]。

棉秆主要使用粉碎还田机进行粉碎还田作业。目前,棉秆粉碎还田机主要分为卧式和立式两种,卧式粉碎还田机由于秸秆粉碎效果更好,成为棉秆粉碎还田的常用机型。近年来,新疆高校、科研院所、山东科研院所等研制的侧抛式棉花秸秆粉碎还田机、二次抛送式棉秸秆粉碎还田机、4JSM-2000型棉秆粉碎与残膜回收联合作业机、平作区棉秆粉碎与残膜回收联合作业机等机型均为卧式粉碎还田机,以上机型均进行了田间试验,得出了该机型的工作参数[10-12]。但是,由于缺乏棉秆粉碎还田理论的研究与分析,棉秆粉碎还田装备主要采用玉米等粉碎还田装备进行改造或者根据经验数据进行设计的,导致棉秆粉碎还田效果差、相关装备可靠性差等。

为解决以上问题,本文采用设计的棉秆粉碎还田机,进行了棉秆粉碎还田单因素和Box-Behnken试验,建立了粉碎辊转速、甩刀离地高度、机具前进速度(试验因素)与棉秆粉碎长度合格率、棉秆抛撒不均匀度、留茬平均高度(试验性能指标)之间的回归方程,确定各试验因素对试验性能指标的影响规律,并进行优化计算,对优化结果进行试验验证,得出棉秆粉碎还田的最优参数组合,以期提高棉秆的粉碎还田效果,为棉秆粉碎还田装备的设计提供理论指导。

1 棉秆粉碎还田机结构及工作原理

1.1 棉秆粉碎还田机结构

设计的棉秆粉碎还田机为卧式粉碎还田机,包括粉碎辊、机架、限深辊、悬挂架、变速箱、甩刀等(图1)。

(a) 棉秆粉碎还田机

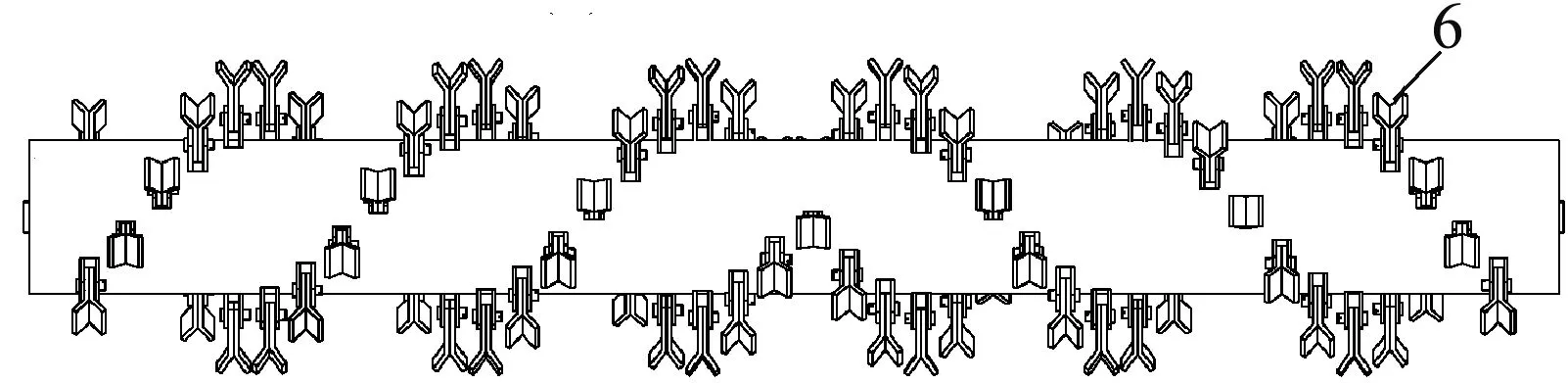
(b) 粉碎辊

其中,粉碎辊为棉秆粉碎还田机的主要工作部件,为使粉碎辊具有较高的粉碎质量,机具在工作时有较好的动平衡性、稳定性且不易发生堵塞,甩刀在粉碎辊上呈双螺旋对称排列[13];为保证粉碎辊具有较高的粉碎效率,且避免甩刀被棉秆缠绕,甩刀采用Y型组合式,排列密度约为0.028片/mm[14],如图1(b)所示。

1.2 棉秆粉碎还田机工作原理

棉秆粉碎还田机的工作原理是机具工作时通过悬挂架与拖拉机进行挂接,拖拉机后输出轴动力通过变速箱传递给粉碎辊,使粉碎辊高速旋转,Y型组合式甩刀随着粉碎辊进行高速转动,在拖拉机前进的同时,在粉碎辊高速旋转形成的负压、棉秆惯性力、机架形成的密闭空间和与甩刀配合的定刀的综合作用下,进入机具的棉秆经过多次砍切、撞击、揉搓后被粉碎,随后在重力和离心力的作用下均匀地落在田间。

棉秆粉碎还田机的主要技术参数见表1。

表1 棉秆粉碎还田机的主要技术参数Tab. 1 Main parameters of cotton stalk chopping and returning machine

2 棉秆粉碎还田试验

2.1 试验基本条件

试验地点在山东省滨州市杨柳雪镇,试验时间为2020年11月,棉花品种为鲁棉338,种植模式为760 mm等行距,种植密度为90 000～120 000株/hm2,棉秆平均高度为875 mm,平均直径为14.5 mm,平均含水率为47.6%,配套拖拉机为福田雷沃欧豹820。

2.2 试验方案

根据农作物秸秆粉碎还田影响因素及作业质量要求[15],本文选取粉碎辊转速、甩刀离地高度、机具前进速度作为试验因素,棉秆粉碎长度合格率、棉秆抛撒不均匀度、留茬平均高度作为试验性能指标。

采用5点法进行各试验性能的测定,即将试验区域对角线中心点和对角线四分之一至八分之一长度范围处的4个点作为测定点,每个测定点随机选取1 m2的统计区域进行相关数据统计。棉秆粉碎长度合格率和棉秆抛撒不均匀度的测定同时进行,捡拾每个统计区域粉碎棉秆的总质量,从中挑选出粉碎长度不合格的棉秆进行称重,按式(1)进行计算[16];测定每个统计区域内所有棉秆留茬高度并计算其平均值,最后将5个测定点的棉秆留茬高度平均值作为棉秆留茬平均高度。

(1)

式中:Mzi——第i个测定点粉碎棉秆总质量,kg;

Mbi——第i个测定点粉碎长度不合格棉秆总质量,kg;

M——试验区域粉碎棉秆质量平均值,kg;

Y1——棉秆粉碎长度合格率,%;

Y2——棉秆抛撒不均匀度,%。

2.2.1 单因素试验方案

棉秆粉碎还田单因素试验因素和水平见表2。进行粉碎辊转速单因素试验时,甩刀离地高度为65 mm,机具前进速度为1.6 m/s;进行甩刀离地高度单因素试验时,粉碎辊转速为2 100 r/min,机具前进速度为1.6 m/s;进行机具前进速度单因素试验时,粉碎辊转速为2 100 r/min,甩刀离地高度为65 mm。

表2 棉秆粉碎还田试验的试验因素与水平Tab. 2 Test factors and levels of cotton stalk chopping and returning to field test

试验时,每组试验选取10个试验区域,重复进行10次试验,单独统计10次试验的相关数据。采用SPSS统计分析软件对单因素试验数据进行统计分析[17],以P<0.05为差异有统计学意义。

2.2.2 响应面法试验方案

单因素试验只能说明单个试验因素对试验性能指标的影响关系与影响程度,并不能说明试验因素之间交互作用对试验性能指标的影响[18]。因此,在单因素试验分析结果的基础上,进行Box-Behnken试验设计,采用3因素3水平的响应面法对试验结果进行分析,建立各试验因素和试验性能指标之间的回归方程,确定各试验因素对试验性能指标的影响规律,建立目标函数并进行优化计算,最后对优化结果进行试验验证,得出棉秆粉碎还田的最优参数组合。Box-Behnken试验的试验因素编码见表3。

表3 Box-Behnken试验的试验因素编码Tab. 3 Test factor code of Box-Behnken test

试验时,每组试验选取10个试验区域,重复进行10次试验,单独统计10次试验的相关数据,将10次试验的平均值作为这组试验的最终试验数值。

3 棉秆粉碎还田试验结果与分析

3.1 单因素试验结果与分析

3.1.1 单因素试验结果

采用均值±标准差的方式表示单因素试验中各试验性能指标的结果,试验结果见表4。

表4 单因素试验结果Tab. 4 Single factor test results

分析表4可知,粉碎辊转速与棉秆粉碎长度合格率的均值成正相关,与棉秆抛撒不均匀度和留茬平均高度的均值呈反相关,说明粉碎辊转速越高,棉秆粉碎效果越好、抛撒越均匀、留茬高度越小。因此,粉碎辊转速越高越有利于棉秆粉碎还田作业。

甩刀离地高度与棉秆抛撒不均匀度的均值呈反相关,与留茬平均高度的均值呈正相关,说明甩刀与地面之间的距离越大,粉碎后的棉秆抛撒越均匀,而留茬高度也越大;当甩刀离地高度为45 mm时,棉秆粉碎长度合格率最大,棉秆粉碎效果最好;当甩刀离地高度为45 mm时,留茬平均高度最小。因此,棉秆粉碎还田作业时,必须选取一个合适甩刀离地高度,在保证棉秆粉碎效果尽可能好、抛撒尽可能均匀的同时,留茬高度尽可能小。

机具前进速度与棉秆粉碎长度合格率的均值呈反相关,说明机具前进速度越慢,棉秆粉碎效果越好;当机具前进速度为1.30 m/s时,棉秆抛撒不均匀度最小,即棉秆抛撒最均匀;当机具前进速度为1.60 m/s时,留茬平均高度最小。因此,棉秆粉碎还田作业时,也必须选取一个合适的机具前进速度,在保证棉秆粉碎效果尽可能好、抛撒尽可能均匀的同时,留茬高度尽可能小。

3.1.2 单因素试验结果分析

采用SPSS统计分析软件对采集的试验数据进行单因素统计分析,验证单个试验因素对每个试验性能指标是否具有影响及显著性程度,分析结果见表5。

表5 单因素试验结果分析Tab. 5 Analysis of single factor test results

从表5可看出,单个试验因素对每个试验性能指标均有影响且影响均显著(P<0.05)。根据F值的大小可知,粉碎辊转速对每个试验性能指标的影响顺序为:棉秆粉碎长度合格率>棉秆抛撒不均匀度>留茬平均高度;甩刀离地高度对每个试验性能指标的影响顺序为:留茬平均高度>棉秆抛撒不均匀度>棉秆粉碎长度合格率;机具前进速度对每个试验性能指标的影响顺序为:棉秆粉碎长度合格率>棉秆抛撒不均匀度>留茬平均高度。

3.2 响应面法试验结果与分析

根据制定的响应面法试验方案进行Box-Behnken试验设计并进行试验,试验结果见表6。

表6 响应面法试验结果Tab. 6 Response surface method test results

根据Box-Behnken试验设计和试验结果,采用二次线性回归建立各试验性能指标与各试验因素之间的关系模型并进行方差分析,方差分析结果见表7～表9。根据方差分析中的失拟项、信噪比和相关系数R2等可判断所建立的关系模型是否可用于预测相关试验性能指标,所预测数据与试验数据的拟合程度[19-20]。

表7 棉秆粉碎长度合格率的响应面方差分析Tab. 7 Response surface variance analysis of qualified rate of cotton stalk chopping length

表8 预测最优值和试验最优值的对比Tab. 8 Comparison of predicted and test optimal value

表8 棉秆抛撒不均匀度的响应面方差分析Tab. 8 Response surface variance analysis of spreading unevenness of cotton stalk

表9 留茬平均高度的响应面方差分析Tab. 9 Response surface variance analysis of average height of stubble

通过表7～表9可知,建立的棉秆粉碎长度合格率、棉秆抛撒不均匀度和留茬平均高度的关系模型均是极显著的(P<0.01);所建立各关系模型的失拟项均不显著(P>0.05),信噪比均大于18,表明建立的关系模型是合理且较优的,可用于预测相关试验性能指标;相关系数R2和调整后的R2均大于0.9,表明所建立关系模型的预测数据与试验数据具有较高的拟合度。

根据响应面试验结果绘制相应的响应面图,响应面图表达了当其他试验因素为0水平(机具前进速度1.6 m/s、甩刀离地高度60 mm和粉碎辊转速2 000 r/min)时,其他两个试验因素的交互作用与试验性能指标之间的关系。

1) 建立的试验因素与棉秆粉碎长度合格率之间的关系模型

Y1=90.07+2.30X1-0.51X2+0.65X3+

X1X2+0.75X1X3-1.50X2X3-

1.10X12+1.93X22+0.835 0X32

(2)

通过表7可知,粉碎辊转速和甩刀离地高度(X1X2)、粉碎辊转速和机具前进速度(X1X3)的相互作用对棉秆粉碎长度合格率具有显著影响(P<0.05),甩刀离地高度和机具前进速度(X2X3)的相互作用对棉秆粉碎长度合格率具有极显著影响(P<0.01)。棉秆粉碎长度合格率与试验因素的响应面图如图2所示。

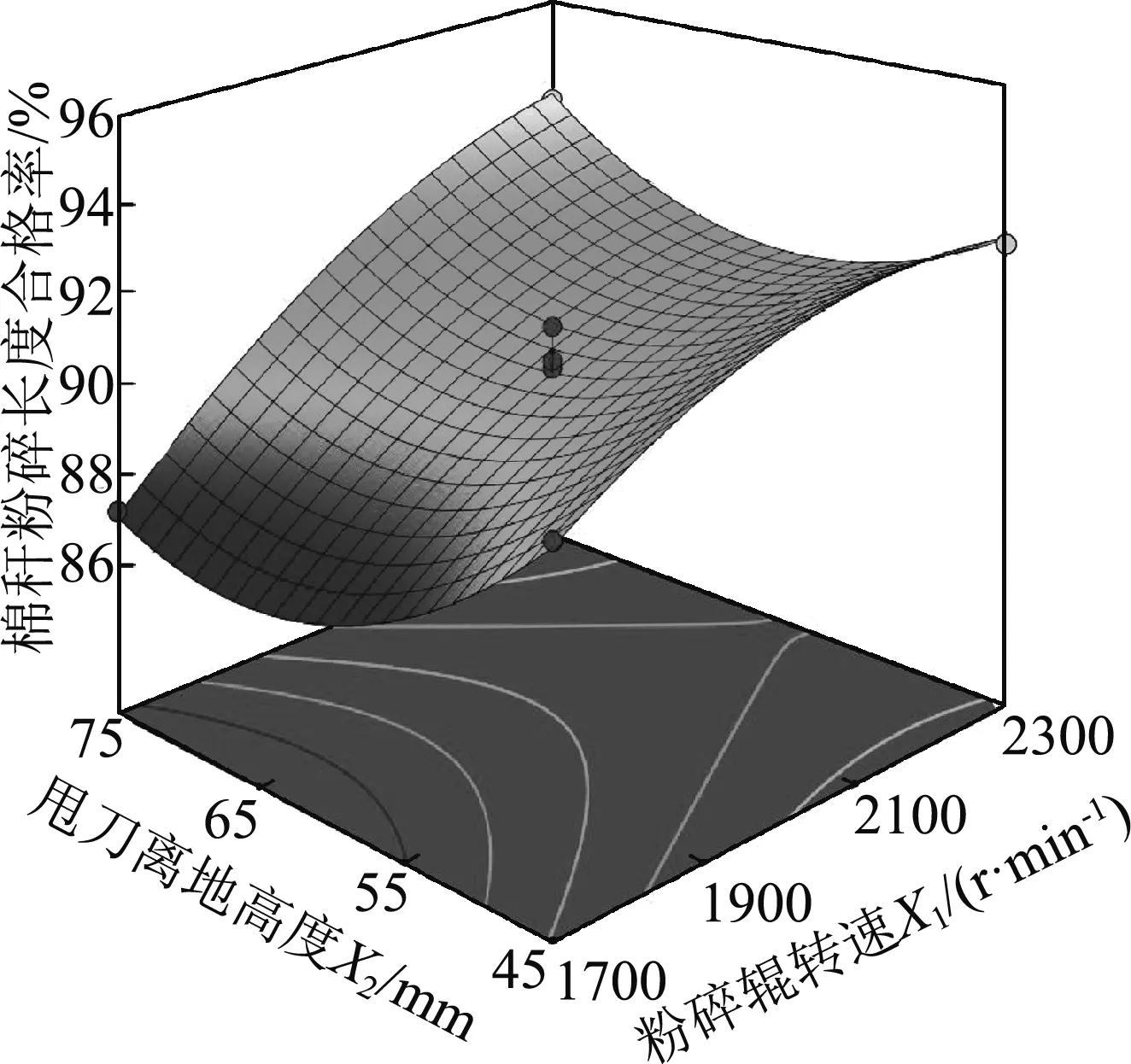
(a) X1与X2的交互作用

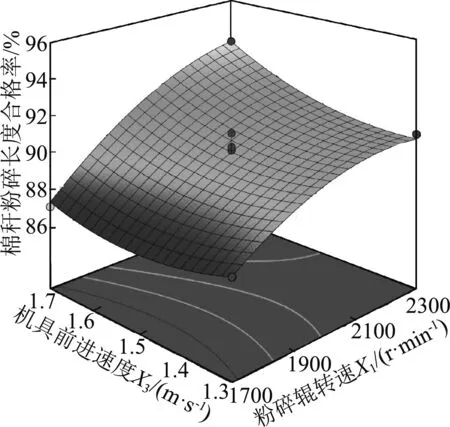
(b) X1与X3的交互作用

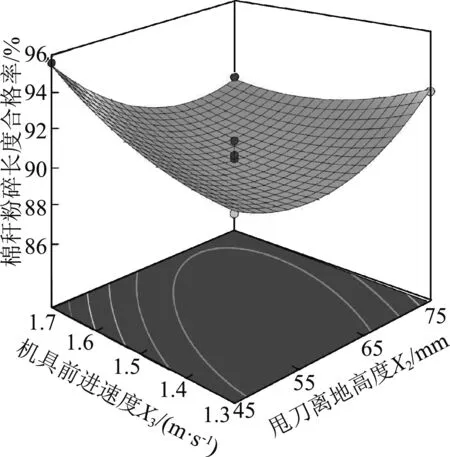
(c) X2与X3的交互作用

分析图2可知,在交互试验因素的影响下,随着粉碎辊转速的增大,棉秆粉碎长度合格率先增大后减小,这与单因素分析时粉碎辊转速与棉秆粉碎长度合格率的均值成正相关的结论不一致;随着甩刀离地高度和机具前进速度的增大,棉秆粉碎长度合格率先减小再增大,这与单因素分析时机具前进速度与棉秆粉碎长度合格率的均值呈反相关的结论不一致。以上结论说明试验因素的交互作用对棉秆粉碎长度合格率有影响,与表7中的方差分析结果一致。

分析图2(a)可知,粉碎辊转速和甩刀离地高度对棉秆粉碎长度合格率的响应面呈凹陷状,表明这两者的交互作用对棉秆粉碎长度合格率的影响较强;粉碎辊转速的曲面相对于甩刀离地高度的曲面较陡,表明在交互作用下,粉碎辊转速对棉秆粉碎长度合格率的影响比甩刀离地高度大。

分析图2(b)可知,粉碎辊转速和机具前进速度对棉秆粉碎长度合格率的响应面呈凹陷状,表明这两者的交互作用对棉秆粉碎长度合格率的影响较强;粉碎辊转速的曲面相对于机具前进速度的曲面较陡,表明在交互作用下,粉碎辊转速对棉秆粉碎长度合格率的影响比机具前进速度大。

分析图2(c)可知,甩刀离地高度和机具前进速度对棉秆粉碎长度合格率的响应面呈凹陷状,表明这两者的交互作用对棉秆粉碎长度合格率的影响较强;机具前进速度的曲面相对于甩刀离地高度的曲面较陡,表明在交互作用下,机具前进速度对棉秆粉碎长度合格率的影响比甩刀离地高度大[21-22]。

2) 建立的试验因素与棉秆抛撒不均匀度的关系模型

Y2=13.41-2.41X1-0.45X2-0.57X3+

0.67X1X2+1.50X1X3-0.84X2X3+

0.96X12-0.61X22+1.03X32

(3)

通过表8可知,粉碎辊转速和甩刀离地高度(X1X2)、甩刀离地高度和机具前进速度(X2X3)的相互作用对棉秆抛撒不均匀度具有显著影响(P<0.05),粉碎辊转速和机具前进速度(X1X3)的相互作用对棉秆抛撒不均匀度具有极显著影响(P<0.01)。因此,绘制的棉秆抛撒不均匀度与试验因素的响应面图如图3所示。

(a) X1与X2的交互作用

(b) X1与X3的交互作用

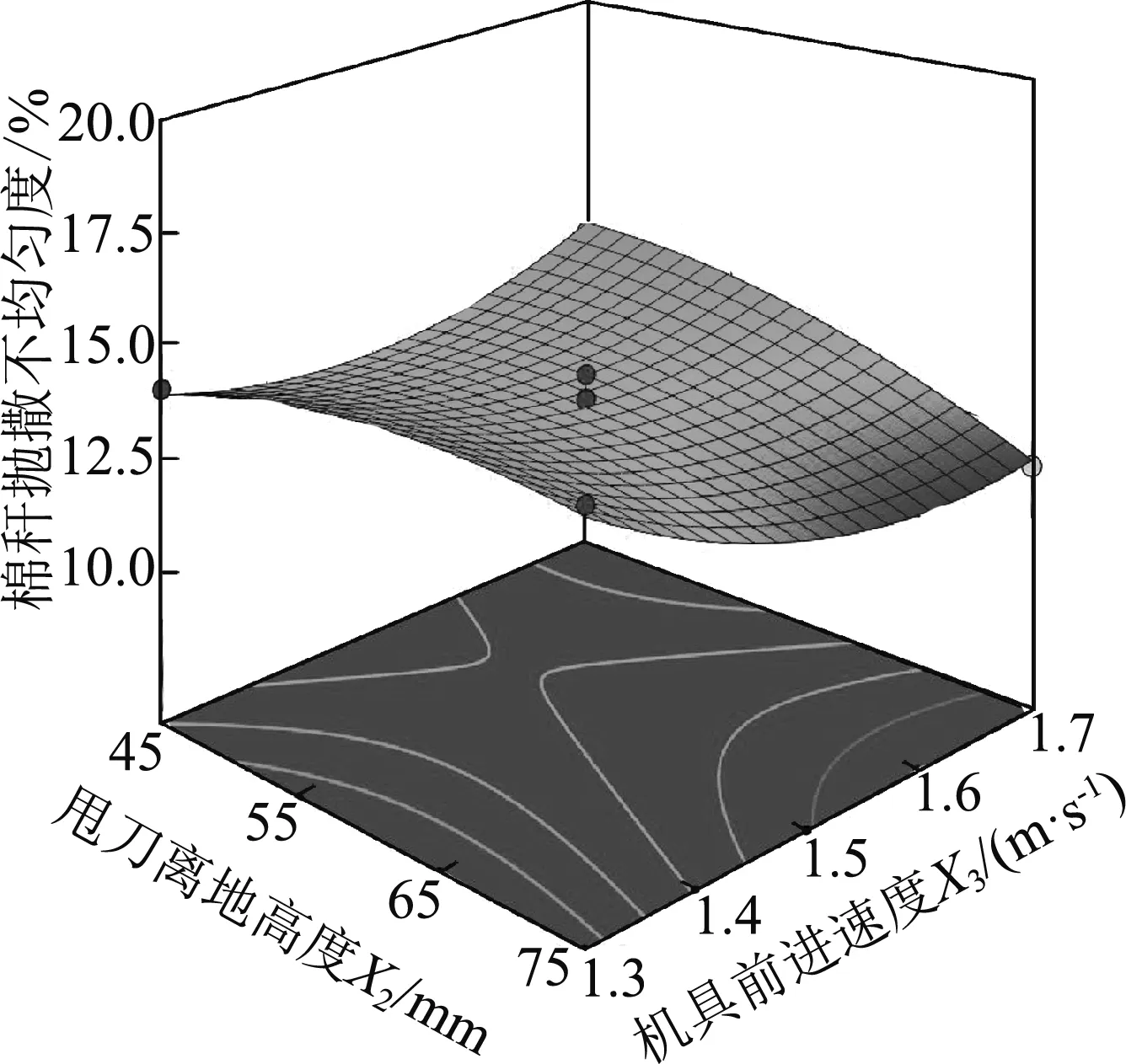
(c) X2与X3的交互作用

分析图3可知,在交互试验因素的影响下,随着粉碎辊转速和机具前进速度的增大,棉秆抛撒不均匀度先减小后增大,这与单因素分析时粉碎辊转速与棉秆抛撒不均匀度的均值呈反相关的结论不一致;随着甩刀离地高度的增大,棉秆抛撒不均匀度先增大后减小,这与单因素分析时甩刀离地高度与棉秆抛撒不均匀度的均值呈反相关的结论不一致。以上结论说明试验因素的交互作用对棉秆抛撒不均匀度有影响,与表8中的方差分析结果一致。

分析图3(a)可知,粉碎辊转速和甩刀离地高度对棉秆抛撒不均匀度的响应面呈凹陷状,表明这两者的交互作用对棉秆抛撒不均匀度的影响较强;粉碎辊转速的曲面相对于甩刀离地高度的曲面较陡,表明在交互作用下,粉碎辊转速对棉秆抛撒不均匀度的影响比甩刀离地高度大。

分析图3(b)可知,粉碎辊转速和机具前进速度对棉秆抛撒不均匀度的响应面呈马鞍状,表明这两者的交互作用对棉秆抛撒不均匀度的影响较强;粉碎辊转速的曲面相对于机具前进速度的曲面较陡,表明在交互作用下,粉碎辊转速对棉秆抛撒不均匀度的影响比机具前进速度大。

分析图3(c)可知,甩刀离地高度和机具前进速度对棉秆抛撒不均匀度的响应面呈马鞍状,表明这两者的交互作用对棉秆抛撒不均匀度的影响较强;机具前进速度的曲面相对于甩刀离地高度的曲面较陡,表明在交互作用下,机具前进速度对棉秆抛撒不均匀度的影响比甩刀离地高度大。

3) 建立的试验因素与留茬平均高度之间的关系模型

Y3=47.18-4.93X1-2.58X2+1.67X3+

1.50X1X2-1.75X1X3-1.25X2X3+

2.97X12+1.11X22-2.75X32

(4)

根据表9可知,粉碎辊转速和甩刀离地高度(X1X2)、甩刀离地高度和机具前进速度(X2X3)的相互作用对留茬平均高度具有显著影响(P<0.05),粉碎辊转速和机具前进速度(X1X3)的相互作用对留茬平均高度具有极显著影响(P<0.01)。因此,绘制的留茬平均高度与试验因素的响应面图如图4所示。

(a) X1与X2的交互作用

(b) X1与X3的交互作用

分析图4可知,在交互试验因素的影响下,随着粉碎辊转速的增大,留茬平均高度先减小后增大,这与单因素分析时粉碎辊转速与留茬平均高度的均值无明显规律的结论不一致;随着甩刀离地高度的增大,留茬平均高度也增大,这与当因素分析时甩刀离地高度与留茬平均高度的均值呈正相关的结论一致;随着机具前进速度的增大,留茬平均高度先增大后减小,这与当因素分析时机具前进速度与留茬平均高度的均值呈先减小后增大的结论不一致。以上结论说明试验因素的交互作用对留茬平均高度有影响,与表9中的方差分析结果一致。

x

分析图4(a)可知,粉碎辊转速和甩刀离地高度对留茬平均高度的响应面呈凹陷状,表明这两者的交互作用对留茬平均高度的影响较强;粉碎辊转速的曲面相对于甩刀离地高度的曲面较陡,表明在交互作用下,粉碎辊转速对留茬平均高度的影响比甩刀离地高度大。

分析图4(b)可知,粉碎辊转速和机具前进速度对留茬平均高度的响应面呈马鞍状,表明这两者的交互作用对留茬平均高度的影响较强;粉碎辊转速的曲面相对于机具前进速度的曲面较陡,表明在交互作用下,粉碎辊转速对留茬平均高度的影响比机具前进速度大。

分析图4(c)可知,甩刀离地高度和机具前进速度对留茬平均高度的响应面呈马鞍状,表明这两者的交互作用对留茬平均高度的影响较强;甩刀离地高度的曲面相对于机具前进速度的曲面较陡,表明在交互作用下,甩刀离地高度对留茬平均高度的影响比机具前进速度大。

3.3 模型验证与参数优化

3.3.1 模型验证

本文采用试验数据与模型预测数据之间的绝对误差比验证所建立模型的可参考度,绝对误差比

式中:φi——绝对误差比,%;

ai——试验性能指标的试验数据;

Ai——试验性能指标的模型预测数据。

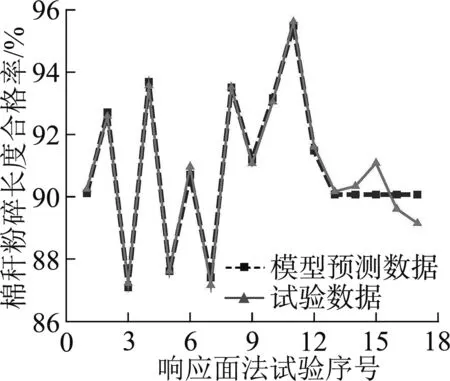
试验数据与模型预测数据曲线对比图如图5所示。通过图5可知,棉秆粉碎长度合格率、棉秆抛撒不均匀度和留茬平均高度的最大绝对误差比分别为1.11%、7.88%和2.62%,均小于8%,在考虑范围之内,表明各试验性能指标的模型预测数据与试验数据拟合程度比较高,所建立的模型可参考度高。

(a) 棉秆粉碎长度合格率

(b) 棉秆抛撒不均匀度

3.3.2 参数优化

通过建立目标函数,利用Design-Expert软件的目标优化法,得出最优的试验因素和对应的试验性能指标值。

建立的目标函数如下

(6)

根据建立的目标函数,得出各试验性能指标的预测最优值,然后根据预测最优值进行试验验证得到棉秆粉碎还田作业的试验最优值(表8)。预测最优值与试验最优值的绝对误差比均小于4.50%,在考虑的误差范围内,表明棉秆粉碎还田的最优值为粉碎辊转速为2 290 r/min,甩刀离地高度45 mm,机具前进速度1.58 m/s,棉秆粉碎长度合格率95.13%,棉秆抛撒不均匀度12.16%,留茬平均高度42.13 mm。

4 结论

本文通过棉秆粉碎还田单因素和Box-Behnken试验,采用SPSS统计软件中单因素方法和Design-Expert软件中响应面法分析了试验数据,优化得出了棉秆粉碎还田的最优值,并进行了试验验证,得出如下结论。

1) 通过单因素试验分析,粉碎辊转速、甩刀离地高度、机具前进速度对棉秆粉碎长度合格率、棉秆抛撒不均匀度和留茬平均高度之间均具有显著影响。

2) 通过Box-Behnken试验分析,建立了粉碎辊转速、甩刀离地高度、机具前进速度与棉秆粉碎长度合格率、棉秆抛撒不均匀度和留茬平均高度之间的二次回归方程,拟合程度均比较高,可用于预测相关数值。

3) 确定了棉秆粉碎还田作业的最优值为粉碎辊转速为2 290 r/min,甩刀离地高度45 mm,机具前进速度1.58 m/s,棉秆粉碎长度合格率95.13%,棉秆抛撒不均匀度12.16%,留茬平均高度42.13 mm。