螺旋桨对船舶操纵运动水动力影响的数值研究

于子涵,邹早建,2

(1.上海交通大学 船舶海洋与建筑工程学院,上海 200240;2.上海交通大学 海洋工程国家重点实验室,上海 200240)

在船舶操纵过程中,船体、螺旋桨、舵三者之间的相互作用非常明显。由于船体、螺旋桨、舵在操纵工况下受到复杂入流的影响,使得船-桨-舵相互作用相当复杂,船舶水动力特性发生显著变化[1],并对船舶操纵性产生重要影响。因此,深入研究操纵工况下的船-桨-舵相互作用,对于准确预报船舶操纵性至关重要。

应用CFD方法模拟约束模试验是研究操纵工况下的船-桨-舵相互作用的一种有效方法。Badoe等[2]使用OpenFOAM中的RANS求解器对船-桨-舵系统的斜拖试验进行了数值模拟,分析了漂角和船体外形对舵及螺旋桨性能的影响;Dai等[3]使用CFD Ship-Iowa软件中的RANS求解器模拟了带螺旋桨和舵的全附体DTMB5617船模的旋臂试验,分析了船体、螺旋桨、舵的水动力与绕流场;Abbas和Kornev[4]使用OpenFOAM中的RANS/LES求解器模拟了全附体KVLCC2船模的斜拖试验和旋臂试验,分析了螺旋桨激振力的变化;侯建军等[5]使用滑移网格与动网格模拟了某双桨双舵船的斜拖试验,研究了船-桨-舵相互作用的流场;王骁等[6]分别采用MRF方法和滑移网格法对螺旋桨建模,对全附体MARIN Model No.7967船模的旋臂试验进行了数值模拟,研究了不同回转半径下船-桨-舵相互作用的流场;Wang等[7]使用Fluent中的RANS求解器模拟了全附体KCS船模的斜拖试验,分析了斜拖试验的螺旋桨激振力;Guo等[8]使用STAR CCM+的RANS求解器模拟了双桨双舵ONRT船模的舵力试验、斜拖试验与旋臂试验,计算了船-桨-舵相互作用系数并建立了描述螺旋桨侧向力和舵法向力的数学模型;吴召华等[9]使用Fluent的RANS求解器模拟了全附体3100TEU集装箱船的旋臂试验,分析了体积力法在研究船-桨-舵相互作用问题中的适应性;刘义等[10]使用STAR CCM+的RANS求解器模拟了全附体KCS船模的斜拖试验,分别采用体积力法和实桨建模法对螺旋桨建模,验证了体积力法具有可接受的数值精度。

前人的研究集中在静态约束模试验中船体、螺旋桨、舵三者水动力的变化,但考虑螺旋桨对静态约束模试验中船体水动力、力矩和舵法向力的影响的研究相对较少。本文以集装箱船KCS(KRISO Container Ship)船模为研究对象,应用CFD软件STAR CCM+的RANS求解器,采用体积力法对螺旋桨进行建模,分别对带螺旋桨和舵的全附体KCS船模以及只带舵的KCS船模进行静态约束模试验数值模拟,包括舵力试验、零舵角斜拖试验及带不同舵角斜拖试验数值模拟,通过对比研究分析了螺旋桨对船-舵系统水动力的影响。

1 数学模型与数值方法

1.1 坐标系

采用图1所示的惯性坐标系O0-XoY0Z0和随体坐标系o-xyz描述船舶在水平面内的运动,其中,U为船舶在水平面内的合速度,u、v分别为纵向速度分量和横向速度分量;β为漂角,定义从U顺时针转到x轴的方向为正;δ为舵角,定义右舵为正;X和Y为作用在船模上的纵向力和横向力,N为绕z轴的转首力矩;FN为舵的法向力。

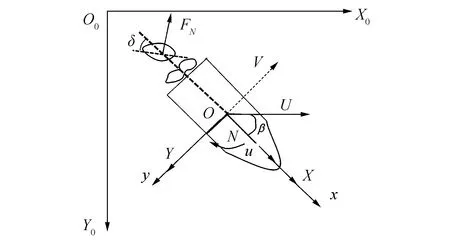
图1 坐标系Fig.1 Coordinate systems

1.2 控制方程

约束模试验中船模的绕流场具有三维不可压缩、黏性流体流场的物理特性,使用雷诺时均连续性方程与动量方程(Navier-Stokes方程)描述：

(1)

1.3 湍流模型

由于式(1)含雷诺应力项,需要引入湍流模型封闭控制方程。本文使用Menter[11]提出的SSTk-ω湍流模型,将适用于近壁面计算的k-ω模型和适用于远场的k-ε模型结合求解：

(2)

式中：k为湍动能;ω为湍动能耗散率;μt为湍流涡动力粘度;σk、σω、β、β*、γ为k-ω模型与k-ε模型结合后的模型参数,其余参数及混合函数的定义为：

(3)

式中：v为运动粘性系数;d为到壁面的距离;φ1对应集合{σk1,σω1,β1,β*,κ,γ1}中的任一参数;φ2对应集合{σk2,σω2,β2,β*,κ,γ2}中的任一参数。各参数的值或表达为：

(4)

(5)

1.4 离散及求解方法

本文采用有限体积法将计算域离散为若干个计算单元。针对每一个计算单元,采用分离型求解器;对流项的离散格式是二阶迎风格式,扩散项的离散格式是二阶中心差分格式;压力与速度的耦合算法采用SIMPLE算法,经迭代后获得数值解。

1.5 螺旋桨模型

使用由Hough等[12]提出的体积力模型对螺旋桨建模,该方法将体积力以源项的形式引入控制方程以替代螺旋桨表面的载荷,其表达式为：

(6)

式中：rc为螺旋桨区域内任取一点到桨轴线的距离;rp为螺旋桨的半径;rh为螺旋桨桨毂的半径;Tp为螺旋桨的推力;QP为螺旋桨的转矩;ΔP为桨盘面的厚度,通常取桨直径的2%;fbx和fbθ分别为轴向力和切向力在螺旋桨区域内的分布。

2 计算设置与网格划分

2.1 研究对象

参考国际船舶操纵性预报方法验证与确认专题研讨会SIMMAN2014的标准算例,全附体KCS船模选择由丹麦福斯科技公司(FORCE)提供的集装箱船KCS(KRISO Container Ship)船模试验数据;只带舵的KCS船模选择由中国船舶科学研究中心(下文简称CSSRC)提供的KCS船模试验数据。FORCE和CSSRC提供的试验数据的模型缩尺比均为1∶52.667,均为静水、深水中的静态约束模试验数据。

全附体KCS船模几何见图2,船型参数见表1。舵剖面采用NACA0018翼型,舵型参数见表2。螺旋桨采用VP1193螺旋桨,桨型参数见表3。

表1 KCS船型主要参数Table 1 Main parameters of the KCS ship

表2 NACA0018舵主要参数Table 2 Main parameters of the NACA0018 rudder

表3 VP1193螺旋桨主要参数Table 3 Main parameters of the VP1193 propeller

图2 全附体KCS船模几何图Fig.2 Geometric graph of fully appended KCS ship model

本文利用由FORCE提供的VP1193螺旋桨敞水性征曲线,采用体积力法对螺旋桨建模。

2.2 计算工况

根据FORCE提供的全附体KCS船模的静态约束模试验数据,选取船速U=1.318 m/s,对应傅汝德数Fr=0.201下的舵力试验、零舵角斜拖试验、带舵角斜拖试验的试验数据。螺旋桨转速与FORCE的螺旋桨转速保持一致,即转速n=840 r/min。

根据CSSRC提供的只带舵的KCS船模的静态约束模试验数据,选取船速U=1.318 m/s,对应傅汝德数Fr=0.201下的舵力试验数据。在数值模拟过程中考虑船体产生的兴波。由于CSSRC缺少只带舵的KCS船模的零舵角斜拖试验及带舵角斜拖试验的试验数据,本文先利用舵力试验数据进行网格收敛性分析,然后模拟只带舵的KCS船模的零舵角斜拖试验及带舵角斜拖试验。

具体计算工况见表4。其中,HPR表示全附体KCS船模;HR表示只带舵的KCS船模。

表4 计算工况汇总Table 4 Summary of calculation conditions

2.3 计算域与边界条件

采用如图3所示的立方体计算域,其具体尺寸为：船前2.5Lpp;船后5Lpp;船体两侧2.5Lpp;自由面以上1.5Lpp;自由面以下2.5Lpp。将计算域的6个面均设置为速度入口;在船模、舵的表面设置无滑移固壁边界条件。为降低计算过程中的数值振荡,分别在计算域的2个侧面、入口、出口处设置消波模块,其数值阻尼长度为1.25Lpp。

图3 计算域及边界条件Fig.3 Computational domain and boundary conditions

2.4 网格划分

采用适应性较好的切割体网格划分整体网格,在船体及舵表面附近的边界层采用棱柱层网格。对船艏、船艉、舵、螺旋桨、螺旋桨尾流、自由面等表面不连续或易产生较大流场变化的区域设置局部加密区,如图4所示。

图4 计算域网格Fig.4 Computational grids

3 网格收敛性验证

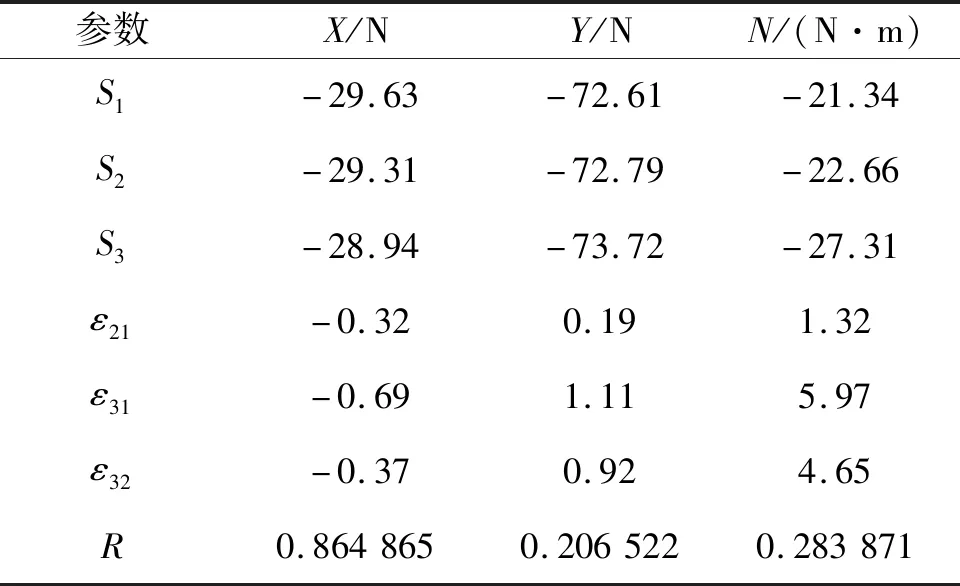
表5 全附体KCS船模的网格尺寸收敛性分析Table 5 Convergence analysis of mesh size for fully appended KCS ship model

表6 只带舵的KCS船模的网格尺寸收敛性分析Table 6 Convergence analysis of mesh size for KCS ship model with only rudder

由GCI准则,全附体KCS船模和只带舵的KCS船模的纵向力X、横向力Y、转首力矩N的收敛率R均介于0～1,说明满足单调收敛。综合考虑计算成本与计算精度,后续数值计算中全附体KCS船模和只带舵的KCS船模均采用中等尺寸的网格。

4 结果与分析

本节分别进行了有桨和无桨条件下带舵KCS船模的舵力试验、零舵角斜拖试验、不同舵角下的斜拖试验数值模拟,以分析螺旋桨对上述静态约束模试验中船体、舵水动力特性的影响。为便于比较FORCE和CSSRC所提供的试验数据,根据CSSRC提供的无因次公式对全附体KCS船模和只带舵的KCS船模的数值结果进行无因次化处理。

船模水动力及力矩的无因次形式为：

(7)

舵法向力的无因次形式为：

(8)

式中U为初始时刻船模的匀速直航速度。

4.1 船模水动力及力矩分析

4.1.1 舵力试验

图5给出了舵力试验水动力及力矩的数值结果。从图中可以看出,数值结果与试验结果的变化趋势较为一致：随着舵角的增大,船模纵向力、横向力和转首力矩及舵法向力的绝对值呈单调增大的趋势,螺旋桨推力呈单调增大的趋势。在-35°舵角和-30°舵角下,计算值与试验值差值偏大,这是由于在大舵角下流动分离现象更为显著,湍流脉动量的影响增大,RANS方法的数值精度下降。

图5 舵力试验水动力结果比较Fig.5 Comparison of hydrodynamic forces in rudder force test

在安装了螺旋桨后,船模的纵向力、横向力和转首力矩绝对值均有显著的增大,船后舵的法向力绝对值也显著增大,说明螺旋桨的运转提高了舵效。各水动力及力矩随舵角变化曲线的斜率增大,说明全附体KCS船模的水动力及力矩对舵角的变化更加敏感。

4.1.2 零舵角斜拖试验

图6给出了零舵角斜拖试验水动力及力矩的数值结果。从图中可以看出,对于全附体KCS船模,纵向力在负漂角下的计算结果与试验数据更为吻合;横向力、转艏力矩的计算结果均与试验数据保持了一致的趋势。由于体积力法缺乏对螺旋桨几何的精确模拟,采用附加体积力源项的方式简化了螺旋桨的几何建模,故螺旋桨负荷的计算值与试验值存在一定的误差。

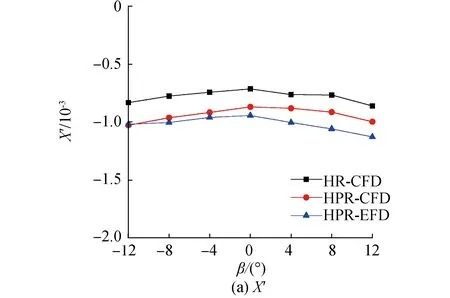
图6 零舵角斜拖试验水动力结果比较Fig.6 Comparison of hydrodynamic forces in oblique-towing test with 0° rudder angle

相较于舵力试验,斜拖试验下螺旋桨的运转对带舵的KCS船模横向力、转艏力矩的影响较小,而纵向力的绝对值呈显著增大的趋势;正漂角下舵法向力的绝对值呈显著增大的趋势,但负漂角下舵法向力的绝对值变化较小,其原因是在横向入流影响下螺旋桨旋向导致作用在桨后舵表面的艉流沿舵的正压面和负压面分布不均。

4.1.3 变舵角斜拖试验

图7给出了不同舵角下的斜拖试验水动力及力矩的数值结果。其中,漂角β=4°下变舵角的全附体KCS船模的计算结果与FORCE提供的试验数据进行了比对。从图中可以看出,计算值与试验值的整体趋势较为一致;在相同舵角下,随着漂角β由-12°变化到4°,船模纵向力绝对值、横向力绝对值、转艏力矩、舵法向力绝对值均呈先减小后增大的趋势,与零舵角斜拖试验的变化规律保持了一致;在相同的漂角下,随着舵角δ由0°变化到-35°,船模纵向力和横向力、舵的法向力呈沿横坐标轴负方向单调减小的趋势,而转首力矩呈沿横坐标轴负方向单调增大的趋势,与舵力试验中的变化规律保持了一致。

图7 不同舵角下的斜拖试验水动力结果比较Fig.7 Comparison of hydrodynamic forces in oblique- towing test with different rudder angles

在安装螺旋桨后,船模的纵向力、横向力和转艏力矩以及舵的法向力绝对值均呈显著增大的趋势,与上文中舵力试验的计算结果变化规律保持了一致。这进一步说明,在安装螺旋桨后,相比于漂角的变化,全附体KCS船模水动力及力矩对舵角的变化更加敏感。

4.2 不同试验的横向力分布对比

横向力是船舶操纵运动中关键的水动力之一,其大小和沿船长的分布情况对船舶操纵性有着重要的影响。本小节分别给出了有桨和无桨条件下横向力沿船长方向的分布并进行讨论。图8～10分别给出了舵力试验、零舵角斜拖试验和变舵角斜拖试验的计算结果,其中横坐标为沿船长方向的无因次纵向位置(设置水线面与船艉柱的交点为坐标原点)。

图8 舵力试验横向力计算结果比较Fig.8 Comparison of computed lateral forces in rudder force test

从图8可以看到,舵力试验中,横向力主要由船艉部区域(0～0.2Lpp)产生,船体其他区域(0.2Lpp～1.0Lpp)的横向力接近于0。随着舵角的增大,船艉部区域的横向力绝对值呈增大的趋势,其他区域的横向力仍接近于0。螺旋桨的运转使船艉部区域(0～0.2Lpp)的横向力绝对值显著增大,对船体其他区域(0.2Lpp～1.0Lpp)的横向力影响较小。

从图9可以看到,零舵角斜拖试验中,在船艏部区域(0.8Lpp～1.0Lpp)产生了较大的横向力,且在约0.95Lpp附近出现了峰值;在船舯平行中体、船艉部等其他区域(0～0.8Lpp),也产生了一定的横向力。总体上,船舯后方区域(0～0.5Lpp)的横向力要小于船舯前方区域(0.5Lpp～1.0Lpp)的横向力。

图9 零舵角斜拖试验横向力计算结果比较Fig.9 Comparison of computed lateral forces in oblique-towing test with 0° rudder angle

安装了螺旋桨后,船艉部区域(0～0.2Lpp)的横向力绝对值显著增大,但船艏部区域(0.8Lpp～1.0Lpp)的横向力没有明显变化。船体0.4Lpp～0.7Lpp区域的横向力有较为明显的变化;当漂角β=-8°或漂角β=-4°时,螺旋桨的运转使得船体0.4Lpp～0.7Lpp区域的横向力绝对值减小;当漂角β=-12°时,螺旋桨的运转对船体0.4Lpp～0.7Lpp区域横向力的影响较小。

从图10可以看到,变舵角斜拖试验中,在船艏部区域(0.8Lpp～1.0Lpp)产生了较大的横向力,且在0.95Lpp附近出现了峰值;船舯后侧区域(0～0.5Lpp)的横向力要小于船舯前侧区域(0.5Lpp～1.0Lpp)的横向力。以上2点规律均与零舵角斜拖试验的计算结果变化规律保持一致。对比图9与图10可以看到,变舵角斜拖试验中船艉部区域(0～0.2Lpp)的横向力绝对值大于零舵角斜拖试验中船艉部区域(0～0.2Lpp)的横向力绝对值。在变舵角斜拖试验中,舵角的变化对船艏部区域(0.8Lpp～1.0Lpp)的横向力影响很小,与舵力试验的计算结果变化规律保持一致。安装螺旋桨后,船艉部区域(0～0.2Lpp)的横向力明显增大,而其他区域的横向力变化较小,这也与舵力试验的计算结果变化规律保持一致。

图10 不同舵角下的斜拖试验横向力计算结果比较Fig.10 Comparison of computed lateral forces in oblique-towing test with different rudder angles

综上,螺旋桨的存在使船艉部区域横向力对舵角的变化更加敏感;随着舵角的增大,船艉部区域横向力增大的速率更快,同时也改变了小漂角斜拖试验中船舯区域的横向力。舵角对于横向力的贡献体现在使船艉部横向力增大,但对船体其他区域的横向力没有产生较大的影响;漂角对于横向力的贡献主要集中在船艏部横向力的峰值点,同时在船艉部和船舯部区域产生了一定的横向力。

4.3 自由面波形

图11给出了全附体KCS船模和只带舵的KCS船模β=-12°下的零舵角斜拖试验自由面波形。从图中可以看到,自由面波形趋于稳定,呈现较为明显的受漂角影响的开尔文波系。相比于只带舵的KCS船模,全附体KCS船模的船艉后方产生了更加强烈的尾流,船艉后方的自由面波形呈现更加明显的峰值点。

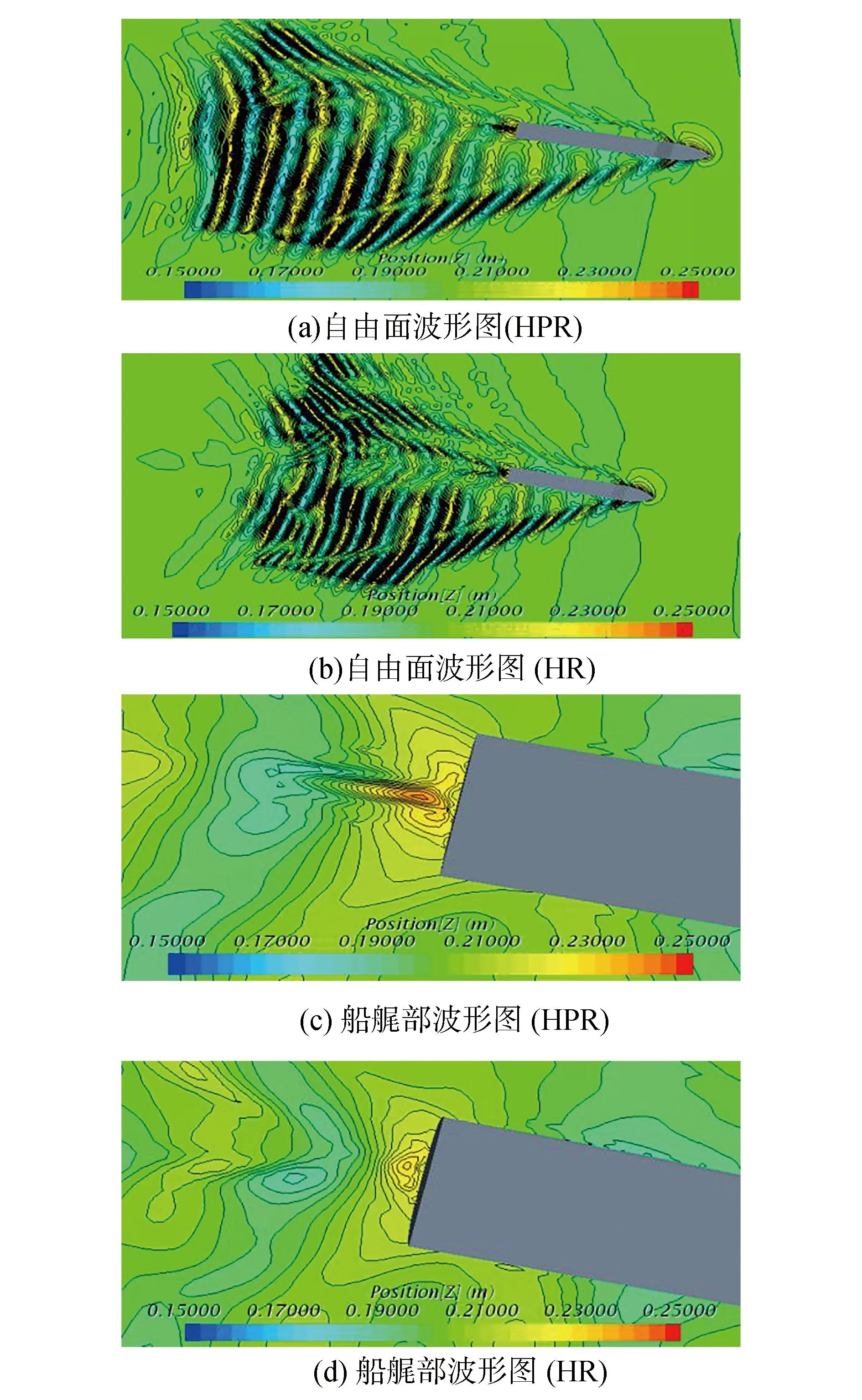
图11 零舵角斜拖试验的自由面波形图(β=-12°)Fig.11 Free surface wave contours in oblique-towing test with 0° rudder angle(β=-12°)

4.4 船体压力分布

图12给出了β=-12°,δ=-35°时斜拖试验的船底区域的压力分布。从图中可以看出,安装螺旋桨后,船底部的高压区有向船舯部集中的趋势,这主要是由螺旋桨的抽吸作用产生的。

图12 沿船长方向压力分布对比(β=-12°,δ=-35°)Fig.12 Comparison of pressure distribution along ship length(β=-12°,δ=-35°)

4.5 船后舵压力分布

图13给出了β=-12°,δ=-35°时带舵角斜拖试验船后舵的压力分布云图。从图中可以看出,安装了螺旋桨后,舵迎流面的正压力显著增大,且高压的峰值区向舵轴附近移动;舵背流面的负压力显著减小,且负压的谷值区向舵导边移动。

图13 船后舵压力分布对比(β=-12°,δ=-35°)Fig.13 Comparison of pressure distribution on the rudder behind the ship(β=-12°,δ=-35°)

4.6 船艉区域纵向速度分布

图14给出了带桨和不带桨的KCS船模在漂角β=-12°和不同舵角下斜拖试验的船艉部纵向速度分布云图。从图中可以看出,对于只带舵的KCS船模,在舵的后缘产生了一个高速区;随着舵角的增大,高速区不断向舵后缘方向移动。安装螺旋桨后,舵后缘高速区产生较为明显的上移,这说明螺旋桨的运转导致舵周围的流动分离现象更为剧烈。在螺旋桨桨轴附近的区域,也产生了一个较为明显的高速区。

图14 不同舵角下斜拖试验的船艉部纵向速度分布对比(β=-12°)Fig.14 Comparison of longitudinal velocity distribution at the stern in oblique-towing test with different rudder angles(β=-12°)

5 结论

1)螺旋桨的运转使得KCS船模的水动力和力矩对舵角的变化更加敏感。在舵力试验、变舵角斜拖试验中,螺旋桨显著增大了船模横向力与转艏力矩;在零舵角斜拖试验中,螺旋桨对KCS船模的横向力与转首力矩影响较小。

2)螺旋桨的运转提高了不同舵角下船后舵的舵效,同时使得漂角大小相同、方向相反的斜拖试验中的舵法向力产生了不对称效应。

3)螺旋桨的运转主要增大了船艉部分的横向力,同时改变了小漂角斜拖试验中船舯附近横向力的分布,但对其他部分的横向力影响较小。

4)螺旋桨的运转显著影响了船后舵周围流场的速度分布,改变了船底部的压力分布。

未来,需要利用更多的全附体船模试验数据开展对比计算研究,以深入研究约束模试验中螺旋桨的水动力特性对船体水动力、力矩以及舵水动力特性的影响。