基于双向蚁群算法的路径规划研究
申铉京,施英杰,黄永平,王玉
(1.吉林大学 计算机科学与技术学院,吉林 长春 130012;2.吉林大学 软件学院,吉林 长春 130012)
蚁群算法[1]是经典的仿生学优化算法之一,与Dijstra[2]、Bellman-Ford[3]以及A*算法[4]等寻路算法相比,在寻求最短路径上始终具有更加优越的效果。
此外,在解决路径问题时,与其他的优化算法如模拟退火算法[5]及遗传算法[6]更具优势。然而,该算法的收敛速度缓慢,陷入局部最优解难以跳出始终都是困扰着蚁群算法效率的一大问题[7]。
针对上述问题,相关学者提出了不同的解决方案[8-9]。针对收敛速度问题,文献[10]在每个路口加入了东南西北4个指针,从而使蚁群在路口时能够优先选择指向终点的路径来提高蚁群算法的效率。然而,该方法所选择的环境为真实道路环境(十字路口等),且仅涉及4个方向,因此将其用于解决机器人路径规划时可能造成陷入局部最优解等问题。在文献[11]中,作者通过利用双向搜索的思想,首先通过A*算法初始化一条次优路径,加强次优路径上的初始信息素的值在初期给蚂蚁一个引导作用防止蚂蚁进行盲目搜索。然后通过改变算法的信息素更新策略提高了算法的搜索精度,但依旧无法解决搜索全局最优解困难的问题。此外,由于A*预处理的存在,导致该方法的解集合可能更小。在文献[12]中,作者引入自适应信息素挥发系数,使信息素挥发系数随着迭代次数发生改变,从而加快了搜索的速度,但在搜索精度方面仍有些许的不足,如在算法前中期无法找到最优解,那本次算法就无法获得全局最优解。文献[13]在信息素更新过程中对最优路径进行信息素奖励,对最差路径进行信息素惩罚,从而提高了算法的搜索速度和收敛能力。但不足之处在于某些情况优先选择离终点较近的节点可能会使蚂蚁走过更长的路径到达终点,且在长的路径上设立了信息素惩罚,在路径搜索时会减小某些同时存在于长路径和最短路径上的节点被选择的概率,会对搜索精度和收敛速度造成影响。
相关学者也提出了许多方法致力于解决算法容易陷入局部最优解以及搜索精度不足等问题。如在在文献[14]中,作者在启发信息中加入了对下一可行节点到目标节点的距离,同时在信息素更新过程中,对最优路径进行奖励而对最差路径进行惩罚减少其路径上的信息素,在路径搜索中有着较为明显的效果提升,但对长路径的信息素惩罚项以及对蚂蚁的死锁处理依旧存在导致其节点选择时容易使蚂蚁错过最短路径。文献[15]中,作者通过控制蚁群的种群相似度来调节解的多样性,并对蚁群算法的信息素更新策略进行调整,有效降低了算法所获得的最短路径的长度。在文献[16]中,作者通过禁忌栅格来避免路径死锁问题,加快了算法的搜索速度,同时采用正反方向蚂蚁,让蚂蚁根据2种不同的搜索策略来进行搜索,有效地提高了算法的收敛速度和搜索精度,然而其采用的折返搜索策略,虽在一定程度上提高了搜索效率,但也增大了算法的搜索时间。在文献[17]中,作者在蚁群的启发函数中加入了当前节点、待选节点以及终点之间的距离关系,并采取信息素扩散方法使某个节点上的信息素向附近节点扩散,从而有效地提高了算法的搜索精度,但同时因为信息素扩散,可能会导致某些差的路径上信息素过大,从而对算法的效率和收敛速度造成影响。文献[18]中,作者通过修改启发式、蚂蚁转移概率及信息素更新公式来提高算法的效率,在最短路径和收敛速度方面都有着不错的提升。
同时也有学者将蚁群算法与其他算法进行融合来解决其收敛速度缓慢以及搜索精度不足的问题[19]。如文献[20]中作者将蚁群算法与萤火虫算法进行融合用来解决车辆路径选择问题,作者在蚁群算法中加入信息素摇动,通过避免信息素在开放区域上停滞而逃脱局部最优。在文献[21]中,作者在势场蚁群算法的基础上提出了基于势场跳转的蚁群算法,将跳点搜索算法引入到鱼群算法中,引入了势场合力递减系数从而减小蚁群陷入局部最优的问题,并对势场蚁群算法的初始信息素浓度、信息素更新策略和启发信息做了一定的改进,使算法的搜索速度有着明显的提升。
在其他领域也存在对于路径规划问题良好解决办法。文献[22]考虑到除路径长度以外的环境因素对最优路径选择所产生的影响,选择的最优路径评价指标不止局限于长度,还包括行走需要的时间、费用以及损耗等问题,并通过实验证明了实时环境下基于多目标的路径选择模型更具有实用价值。该思想同样可应用于机器人路径规划。因此,在最优路径长度相近的情况下,缩小平均转角可以有效减少机器人行走所需要的时间。
通过上述分析,本文提出一种改进蚁群算法用于解决传统蚁群算法收敛缓慢以及搜索精度不足等问题,其基本思想为:让蚂蚁根据编号分别从不同的起始位置出发向起点或终点进行路径搜索,在搜索到对应的路径后根据新的信息素更新规则对全局信息素进行更新。
1)让蚂蚁从地图上非起点和目标节点的可行节点出发,向起点或目标节点去进行搜索,通过让蚂蚁从不同的起点出发来增加解的多样性以获得全局最优解。
2)设立新的全局信息素更新规则,对每次迭代中寻找到的最优路径进行奖励而不对最差路径进行惩罚以增加走过最优路径的蚂蚁对下一轮迭代蚂蚁的引导作用。
3)提出了自适应角度参数并将其使用在蚂蚁转移概率中以提高算法的收敛速度,并与新的信息素更新规则共同作用来降低搜索到的路径的总旋转角度,使机器人在路径上的旋转角度有所下降
最后在Matlab仿真实验中证实了该方法是有效可行的,且寻优效率相对其他算法要高。
1 蚁群算法概述
蚁群算法是一种用来寻找优化路径的概率型算法,是由Dorigo[15]提出的一种仿生学群体智能优化算法,其灵感来源于蚂蚁在觅食过程表现出的群体智能行为,即在蚂蚁觅食过程中,单只蚂蚁的行为比较简单,但是蚁群整体却可以体现一些智能的行为。
1.1 蚁群算法转移概率
蚂蚁在觅食时会在自己走过的路径上留下信息素,而蚁群内的蚂蚁对信息素具有感知能力,它们会沿着不同路径中信息素浓度高的路径行走,每只走过该路径的蚂蚁都会在路径上留下信息素,这样经过一段时间后,蚁群就会沿着最短的路径到达食物源。蚁群算法的转移概率公式为:
(1)
式中:k为当前蚂蚁的编号;α是信息素启发式因子,代表信息素浓度对转移概率的影响。α的值越大,蚂蚁就更倾向于选择其他蚂蚁选择过的路径,搜索的随机性减弱,同时降低了解的多样性,扼杀了一些地图中找到全局最优解的概率。α越小,蚁群的搜索范围也就越小,容易陷入局部最优。τij为i、j路径上的信息素浓度。
信息素浓度β为期望启发因子使算法成为正反馈搜索,该值过大,容易导致蚂蚁选择局部最优路径,虽然收敛速度加快,但无法获得全局最优路径。η为启发函数,其值为i、j两点之间距离的倒数,启发函数的表达式为:
(2)
1.2 信息素的挥发
蚁群在某个节点根据其迁移概率选择下一个需要选择的节点,并在走过的路径上留下信息素。为了防止随着迭代次数增加,路径上的信息素浓度过多,遮盖掉路径上的启发信息,需要在迭代过程中对路径上的信息素进行一定的更新,更新策略为:
τij=(1-ρ)·τij+ρ·Δτij(t)
(3)
式中:ρ是信息素挥发系数,(1-ρ)是信息素的残留系数,如果ρ值过小,会导致路径上信息素残留过多,无法有效区别最短路径和较长路径之间的差距,如果该值过大,在无效路径被排除的同时有可能将有效路径上的信息素也大幅度地消除,增加了算法所需要的时间。Δτ是该条路径上信息素的增量,其值为:
(4)
式中Q为蚁群算法的信息素强度系数。
2 基于角度参数的双向蚁群算法
蚁群算法存在着容易陷入局部最优解、迭代速度慢以及搜索不到最优解等一系列问题,同时在解决静态环境的机器人路径规划中并没有考虑到机器人转动的问题。因此,本文在蚁群算法的基础上提出改进算法用于解决机器人路径规划的问题。本文算法将蚁群的出发位置进行改变以增大蚂蚁的搜索空间来解决蚁群算法初期搜索盲目以及搜索精度不足等问题,使算法在地图中获取更加多样化的解集合,提高了获得全局最优解的概率。同时对蚁群的信息素更新规则进行了改进,增加走过较短路径的蚂蚁的信息素对下轮迭代的作用以解决蚁群算法容易陷入局部最优解无法跳出。提出了角度参数并将其加入到蚂蚁转移概率中,使其能够在蚁群算法的寻路过程中通过角度参数对蚂蚁起到引导作用,让蚂蚁在分叉路口能够更容易的找到距离目标节点较近的路径提高搜索精度,同时能够减少机器人在路径规划中转过的角度总和,从而减小机器人在转弯时所花费的时间。算法伪代码如表1所示,算法流程图如图1所示。

图1 栅格地图Fig.1 Raster map

表1 基于角度参数的双向蚁群算法伪代码Table 1 Pseudocode of bidirectional ant colony algorithm based on angle parameters
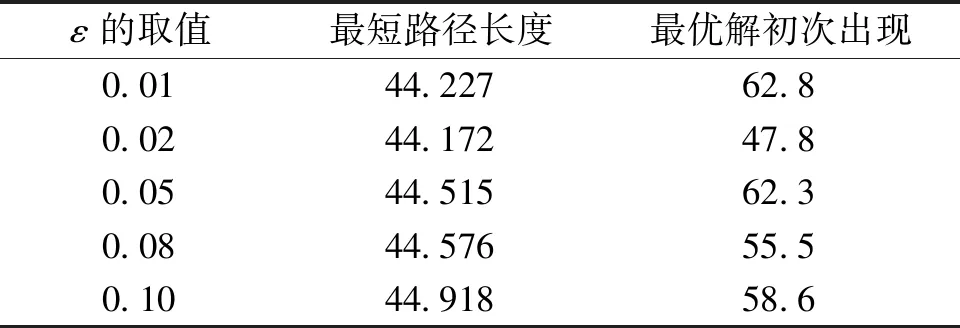
表2 信息素奖励系数算法性能影响Table 2 Pheromone reward coefficient algorithm performance impact
2.1 双向蚁群算法
传统的蚁群算法由于每次进行寻路的蚂蚁都是从固定的起点向终点进行搜索,会导致在算法初期蚂蚁的搜索比较盲目。且在算法的初期,蚂蚁总是在起点附近进行寻找,而距离起点较远的节点却很少有蚂蚁到达,这种情况导致蚁群算法解的多样性较差,且降低了蚁群算法的效率。
文献[11]中采用类似的思想来改进蚂蚁的起始位置,但与本文不同的是,文献[11]将蚂蚁按照编号不同分别放在起点/终点上,再让其向终点/起点进行路径搜索。虽然收敛速度有所降低,但在某些地图中,该算法仍容易使蚁群陷入局部最优而导致其无法获取全局最优解。
针对传统蚁群算法搜索精度不足的问题,本文提出的改进算法对蚂蚁的起始位置进行改进,首先将之前的起点和终点设置为目标点1和目标点2,再将蚂蚁放在栅格地图中的一系列节点所组成的起点集合上,使蚂蚁在起点集合中的不同节点上分别向目标点1或目标点2进行搜索。因此,起始位置的改进不仅增加解的多样性以提高找到最优解的概率,而且还能使每只蚂蚁只搜索半张地图就可以搜索到自己对应的“目的地”,从而缩短蚁群算法的整体时间。
起点集合的选择依据如图1所示,在该栅格地图中,机器人若想从起点到达终点,其可行路线只有包含节点2的A路线和包含节点1的B路线,即不存在一条从起点到终点的路径能够既不包括节点1,也不包括和节点1位于同一行的节点2。同理,大规模的地图上,也不会出现一条从起点到终点的路径能够不包含起点到终点间任意一行或一列中的所有节点。因此在算法中我们只需要将一行或者一列的所有可行节点加入一个集合中,并让蚂蚁从该集合中的点出发向着自己所属的目标节点去寻路,就可以在一次迭代中寻找到从多个起始节点出发的路径,让蚂蚁能在迭代初期就走过一些在蚁群算法中不被考虑的节点,增加解的多样性,从而提高算法的搜索精度和搜索效率。
基于上述起点选择理论,本文所使用的获得起点集合的方法为:对该栅格地图的行和列进行遍历,选择行或列中可行节点最少的一行或一列,将其加入初始节点集合中,在算法的过程中,每只蚂蚁根据自己的编号在起点集合中寻找自己所属的起点,并根据编号寻找自己对应目的地是初始起点还是初始终点。
如图2所示,在进行遍历之后,发现该列是地图中所存在的可行节点最少的一列,因此将该列中的可行节点作为蚂蚁的初始节点结合,开始寻路时,将2只蚂蚁作为蚂蚁1和蚂蚁2放在某一相同起点并开始向各自对应的终点进行路径规划。
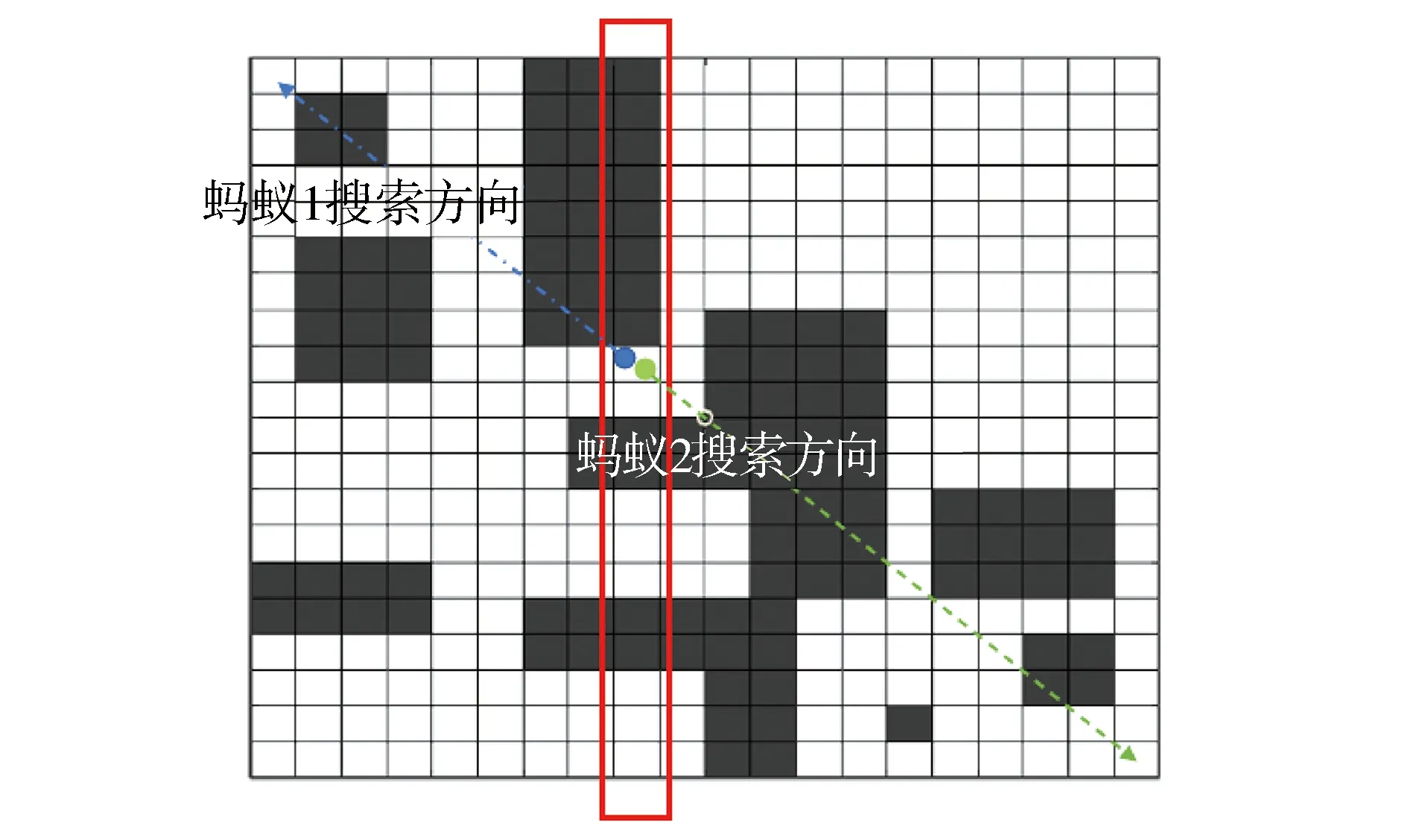
图2 起点集合选择及蚂蚁行走路线Fig.2 Starting point set selection and ant walking route
算法将蚁群需要搜索的地图分为两部分,每只蚂蚁只需要在各自的搜索范围进行搜索。因此,地图两侧的信息素互不干涉,每只蚂蚁只需要维护自己对应搜索范围的信息素矩阵即可。该起点位置改进优势如下:
1)将原本较大的地图分割为2部分较小的地图,使蚂蚁能够更容易搜索到最优解;
2)蚂蚁能够在不同的起点去开始路径搜索,搜索到终点的蚂蚁有权利在自己走过的路径上更新信息素,使得蚁群有全局信息素改变,产生了信息素之间的交流;
3)将地图分为2部分后,各自所持有的信息素相互独立,可以将2部分进行并行计算,相较于传统蚁群算法更加节省时间;
4)让蚂蚁从不同的起点开始进行寻找,增大了解的多样性,提高了获得最优解的概率。
2.2 信息素更新策略的改进
在传统蚁群算法中,信息素的更新策略为只要走到终点的蚂蚁都可以进行信息素更新,并没有体现出走过最短路径的蚂蚁在信息素更新上的优势。因此,本文对信息素更新策略进行了改进,在本次迭代的最短路径上再进行一次信息素更新,以强化最短路径上的信息素以对下一轮迭代的蚂蚁产生影响。
在本文中,向目标节点1和目标节点2进行寻路的蚂蚁分别持有各自的信息素矩阵,并且在本次迭代中所求得的全局最优解的2只蚂蚁未必来源于同一组。因此,本文采取的信息素更新策略为:在本次迭代结束后,先让所有到达自己所属的目标节点的蚂蚁根据所走路径更新信息素,再将从同一起点出发的蚂蚁所获得的路径进行拼接,求出本次迭代中所有蚂蚁所走过的最短路径,并在这些走过最短路径蚂蚁所走过的路径上再进行一次信息素更新,其更新原则:
τij=τij+Δτij(t),i,j∈Lmin
(5)
Δτ(t)=ε*Q*(Lmax-Lmin)/Lmin
(6)
式中:ε为信息素奖励系数Lmax为本次迭代所获得的最大距离,Lmin是本次迭代获得的最短距离;而此信息素更新的值相对比局部信息素更新的差值并不是很大,因此并未在当前迭代次数的最优路径上增加过多信息素以对后来迭代次数的蚂蚁寻路造成决定性的作用,同时也可以在路径上产生一定的信息素增量以给后来的蚂蚁一个引导作用,且随着迭代次数的增加,该增量的值逐渐趋于稳定,不会在后期产生最短路径波动等问题。
在上述信息素更新策略中,不采用信息素挥发系数,因为本策略的目的为在地图上对本次迭代所寻找到的全局最优路径上的信息素给予一定的奖励,如果采取信息素挥发系数对信息素进行处理,则该路径上的信息素浓度相对之前就有所减少,起不到对蚂蚁寻优过程的指引效果。同时在本文的信息素更新策略中,不对走过最长路径的蚂蚁所走过的路径增加惩罚项,因为一旦在初期对其最长路径进行惩罚,就有可能影响获取全局最优路径的概率,从而对算法的效率产生影响。
2.3 融合角度参数的蚂蚁转移概率
为解决蚁群算法的迭代收敛缓慢以及最优解初次出现的迭代次数比较大等问题,本文提出了方向参数并将其加入到蚂蚁转移概率中。在地图中,最容易表示方向的参数就是角度。在机器人寻路过程中,当有多个可行节点供选择时,优先选择与终点更加相近的目标节点,可以使机器人走过更短的路径来到达终点位置。
在机器人的路径规划中,因为机器人的自身问题导致其转弯也需要时间,因此,本文提出的角度参数可以在优先考虑最短距离的同时让机器人走过更小的转角走到终点,可以更有效地减少机器人寻路所需要的时间。
如图3所示,蚂蚁在到达某个节点后,在选择下一个节点时,根据其算法中使用的轮盘赌规则,其节点所对应的概率值越大,则蚂蚁选择该节点的可能性也就越大。同时蚂蚁在当前位置可以沿着①②③④继续寻找下一节点,此时如果使用蚁群算法,则按照轮盘赌的规则,蚂蚁可能选择路径①,则蚂蚁需要在当前位置转弯135°并在路径①上留下信息素,在下一轮迭代中该信息素会继续吸引蚂蚁通过该路径,从而让蚂蚁大概率走过该角度到达终点,而在机器人沿着该路径移动时,在距离相同的条件下,该角度会对机器人的效率造成较大的影响。但在本文算法中采用角度参数来影响蚂蚁的转移概率,即选择和当前节点的连线与当前节点和该蚂蚁目标节点之间的夹角更小的路径去走,这样可以使路径上的总体转弯角度减小。即便当前迭代中,蚂蚁选择了路径①并到达了终点,由于信息素更新规则中的奖励机制使得其除非本次寻找到的是最优路径,否则对下一轮迭代蚂蚁不会造成太大影响。因此,本文提出了角度参数,其具体公式为:

图3 角度参数Fig.3 Angle parameters
(7)
式中a为固定常数,g为自适应参数,根据迭代次数的不同自适应的发生改变,θ为待选择节点和当前节点的连线与当前节点和该蚂蚁目标节点之间的夹角。
由式(1)加入式(7)中的角度参数获得新的蚂蚁转移概率公式为:
(8)
3 仿真实验与分析
3.1 信息素奖励系数的选择
本文设定在不加入角度参数的情况下对信息素奖励系数进行选择,在ε值不同的情况下进行多组对比实验,实验结果如下。
在对ε值进行分析时,当取值为[0.01,0.02]时,算法获得的最短路径长度随着该值的增大而减小,在取值大于0.02后,算法所获得的最短路径长度随着该值的增大而增大,因此,本文将算法的信息素奖励系数设定为0.02,即通过该值对路径上增加的信息素浓度不会对蚂蚁产生决定性的影响,却依旧可以在一定程度上引导蚂蚁选择该较优的路径。
3.2 角度参数的选择
本文在设定g=1的情况下对a值进行选择,因该参数为固定参数,不会在算法进行过程中随着迭代次数的增加而进行改变,因此,该值的选择在一定程度上决定了该角度公式对蚂蚁方向引导的效率。在开放节点较多的地图上进行机器人路径规划时,优先选择偏向目标节点的路径大概率会使机器人走过更短的距离到达目标节点,因此,需要通过该参数来区分出“与目标节点所相近的节点”和那些“偏离目标节点的节点”。
而在实际应用中,通常认为在选择与当前位置和目标节点连线夹角小于90°的路径会使机器人更快到达目标节点,因此应该明确区分出夹角90°以上的路径和夹角为90°以下的路径。
经过一系列Matlab仿真实验的对比,结果如表3及图4所示,在a为1.5时算法的效果最佳,因为当a为1.5的时候刚好能区分出该路径与目标节点和当前节点的连线夹角是否小于90°,当该角度大于90°时,该参数的值小于1,在参数g的作用下,使其能够有效削弱在那些走过与目标节点相反的路径并经过较长路径依然到达终点的蚂蚁在其走过路径上留下的信息素对剩余迭代蚂蚁在路径选择上所造成的影响,而当该角度小于90°时,在真实情况下,走过该条路径的蚂蚁往往能通过更短的路径到达终点。

图4 角度参数中常数a对算法性能影响Fig.4 The influence of the constant a in the angle parameter on the algorithm performance

表3 角度参数中常数a对算法性能影响Table 3 The influence of the constant a in the angle parameter on the algorithm performance
而参数g是根据迭代的过程发生改变的,因此该参数可以对算法前期解的多样性以及算法后期解的收敛性产生较大的影响。
在设定a=1.5的情况下,g值的改变对算法最优解初次出现及收敛速度的影响如表4及图5所示。
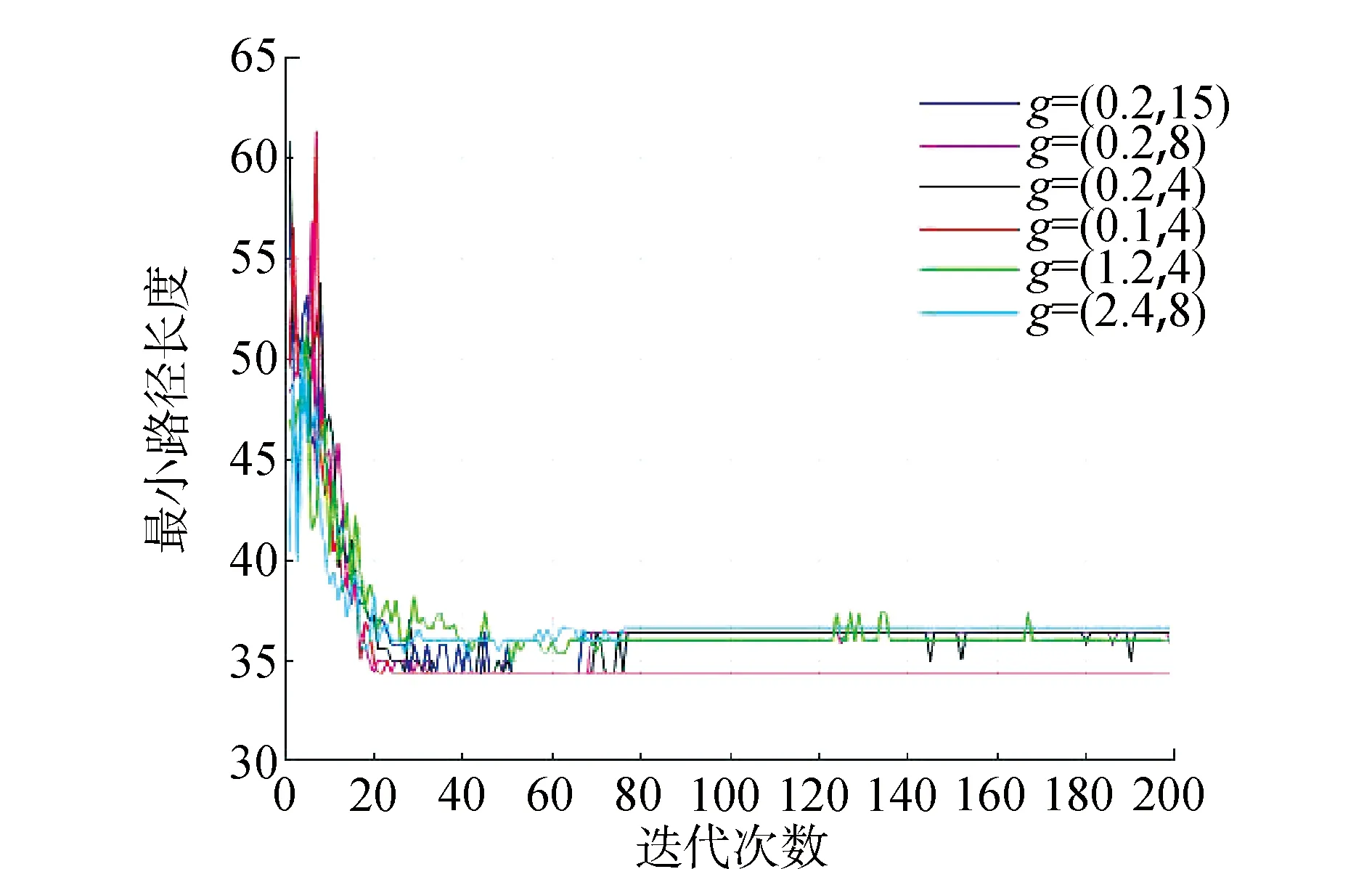
图5 角度参数中参数g对算法性能的影响Fig.5 The influence of the parameter g in the angle parameter on the performance of the algorithm

表4 角度参数中参数g对算法性能的影响Table 4 The influence of the parameter g in the angle parameter on the performance of the algorithm
经过仿真实验的效果对比,最终确定算法初期时将该参数g的取值设置为0来增加解的多样性,在算法进行到中期时将该值设置为1,来加强方向的引导效果,又不会对蚁群对信息素的敏感性造成过多影响,到算法后期,将该值设置为4来加快算法的收敛效果。
如图6所示,在初始条件下,每条路径上初始信息素相等,蚂蚁在角度参数的作用下会优先选择与终点角度相差较小的节点。而某些地图中,这样的节点并不会使的蚂蚁寻找到更好的路径,反而会引导蚂蚁走到一条死路或走过很长的路径到达目标节点,这使得蚂蚁如果从一开始就选择该路径并进行寻找,继而到达目标节点并在该路径下留下信息素,就会造成剩余迭代次数的所有蚂蚁都会被这条较长路径上的信息素影响,无法获得全局最优解。

图6 角度参数可能会产生的影响Fig.6 The possible effect of the angle parameter
在图6所示地图中,第一轮迭代的蚂蚁在角度参数的作用下,会优先选择走到当前节点,继而走到节点1,然后通过一条较长的路径寻到终点并在路径上留下信息素。这样不仅没有提升蚁群搜索的效果,反而降低了搜索的效率,甚至可能在算法初期让蚂蚁走到死路。因此,在算法初期应降低该参数的影响,让蚂蚁能够处于不受其他条件限制的情况下在栅格地图中自由寻找路径,增加了所获得解的多样性,继而增加在算法前期获得最优解的概率。在算法进入中期之后,增大该参数以加强角度的引导,但不能将该值设置的过大,以免对蚂蚁对信息素的敏感性造成影响,从而导致角度的引导性大于信息素的引导性,使算法收敛速度降低的同时影响蚂蚁对最优解的寻找。而在算法后期,则需加大该值以加快算法的收敛速度,若此时在a值相同的情况下该指数不够大,则会对算法的效率产生影响;若该值过大则容易造成信息素和角度参数相互影响,使算法的迭代收敛曲线出现波动且持续不收敛的情况。
3.3 角度算子有效性
在选定了角度公式的参数后,为了验证本文提出的角度参数的有效性,在Matlab仿真环境中且参数相同的情况下做了对比试验。
如图7所示,尽管2种方法均能在多幅栅格地图内找到最小值,但多次试验中,加入角度参数的双向蚁群算法所获得的平均路径长度要更短,且加入角度参数的双向蚁群算法的收敛速度相比于未使用角度参数的双向蚁群算法有着较为显著的提升。因此证明该角度参数的提出及引入是合理且有效的。

图7 角度参数效果对比Fig.7 Comparison of the effect of angle parameters
3.4 算法性能仿真实验
为验证本文改进蚁群算法的有效性,设备条件为:Windows10操作系统,Intel(R) Core(TM) i7-10700F处理器,8 GB内存,在MATLAB R2018仿真环境中分别对蚁群算法,本文算法和文献[11]、文献[12]及文献[14]中的算法在参数相同的情况下,在20×20的地图中和30×30的地图中进行了对比,其中参数设定如表5所示。

表5 对比实验参数设置Table 5 Comparison of experimental parameter settings
算法结果分析如下,其中黑色节点为障碍物节点,白色节点为可行节点,起始坐标均为(1,1)。
从图8、图9及表6中可以看出,在20×20的栅格地图中,本文算法虽与传统蚁群算法转过的平均角度相同,但本文算法求得的最优路径相对蚁群算法却有着较大的改善;本文算法与文献[12]方法相比,在搜索到更短的最短路径的同时,迭代收敛速度也有着明显的增加,转过的平均角度也比文献[12]方法转过的平均角度要低;在本文算法与文献[11]中的算法进行对比时,虽然二者均获得到了相同的全局最优解,但本文算法的平均路径长度、平均转角要远小于文献[11],且收敛速度比文献[11]更快;一系列实验结果证明该改进在小规模地图中是有效的,算法在加入角度参数等改进后,其迭代速度有着明显的提升,且能获得更好的全局最优解,说明其容易陷入局部最优解的问题也得到了改善,同时平均转动角度也有所降低,使得机器人路径规划的总体效率提高。

图8 20×20地图5种算法机器人运动轨迹Fig.8 Robot movement trajectory with five algorithms on 20×20 map

图9 20×20地图5种算法机器人运动收敛趋势对比Fig.9 Comparison of robot movement convergence trends of five algorithms on 20×20 maps

表6 20×20地图6种算法对比实验结果Table 6 Comparison experiment results of six algorithms on 20×20 map
而在与文献[14]中的算法进行对比时,文献[14]中的算法由于在信息素和启发式因子中过多的考虑了待选择节点和目标节点之间的距离,导致其在出现“选择距离目标节点较近的节点会使蚂蚁经过更长的路线到达终点”这类陷阱时,算法的效果较差。而本文算法由于在初期让蚂蚁在不同的起点较为自由的搜索,从而不会出现让其迁移概率过分依赖于与目标节点之间的距离关系这一现象,避免了这种问题的出现。同时,本文方法的旋转角度要比文献[14]中的旋转角度更低,在机器人移动时会更节省时间,提高了机器人移动的效率。在与文献[18]中的算法进行对比时,其收敛速度相对较快,但平均路径长度相对较差,且平均旋转角度相对较多,其原因可能是算法在初期即有方向参数的参与,导致算法在初期就会选择与终点方向夹角小的节点行走,而导致本文3.2中提到的“绕路”现象的发生而造成路径长度增加且转角增多。而本文在对提出的角度参数进行处理时,通过减小其前期对算法的影响,有效的避免了该现象的发生。
如图10、图11和表7所示,在30×30的地图中,本文算法在参数相同的情况下,相较于蚁群算法、文献[11]和文献[12]中的蚁群算法搜索到了更短的全局最短路径,且平均路径及旋转角度相较于其他2种算法也更小;同时由本文算法中所获得的最短路径和平均路径的差值很小可以看出,该方法所获得的解波动不大,从而体现了该方法具有一定的稳定性;且该方法的平均收敛速度相交于蚁群算法也提高了许多。在与文献[14]进行对比时,虽然本文算法与该文献算法都找到了相同的最小路径,但因文献[14]对通过较长路径的蚂蚁所走过的路线设置了惩罚项,导致如果该条路径同时出现在最长路线和最短路线上,其路径上的信息素并没有实质性的奖励,反而可能会减小,从而未能保证每次都能求出最优路线。而本文算法仅对最优路线进行奖励而不对最差路线进行惩罚,使解的多样性得到扩充的同时,减小因惩罚项导致错失最优路径的概率,从而使本文算法的平均路径长度要优于文献[14]。在与文献[18]进行比对时,其结果与20×20类似,其角度参数在初期影响较大而造成一条非最优路径上的信息素过高,导致其结果较差。而本文算法合理的调整了角度参数加入的时机,使算法能寻找到更短的最优路径。且本文算法机器人平均转过的角度相对文献[11-12,14,18]中的要更小,说明该算法能够对机器人路径寻优所走过的角度进行改善,从而提高机器人路径规划的效率。

图10 30×30地图5种算法机器人运动轨迹Fig.10 Robot movement trajectory on 30×30 map

图11 30×30地图中5种算法收敛趋势对比Fig.11 Comparison of convergence trends of five algorithms in 30×30 map

表7 30×30地图6种算法对比实验结果Table 7 Comparison experiment results of six algorithms on 30×30 map
4 结论
1)在蚁群算法的基础上通过将蚂蚁起始位置以及目标位置进行改变并对最短路径上的信息素进行奖励,可以有效提高算法对最优解的搜索。
2)通过加入角度参数,对蚂蚁搜索的过程进行引导,信息素浓度影响蚂蚁对下一节点的选择概率,可以有效解决算法的收敛速度问题。
3)所提出的算法解决了蚁群算法在机器人路径规划中收敛速度慢、容易陷入局部最优解以及精度不足等问题,相比于其他几种改进蚁群算法在机器人路径规划中拥有更好的寻优效果和收敛速度以及更小的转动角度。
如何有效解决动态路径规划问题将成为今后研究的主要工作。

