基于PCA-SSA-PNN 的齿轮故障诊断

陈立爱，俞宏艳，汪佳奇，陈松

安徽建筑大学机械与电气工程学院，安徽 合肥 230601

齿轮作为转速调节和动力传递的常用部件，其是否正常运行将影响机电设备的工作状态［1-3］。齿轮在工作过程中发生故障的概率较高，因此对齿轮进行故障诊断尤为重要［4-5］。

齿轮故障诊断方法主要包括信号处理和机器学习两大类，信号处理方法包括傅里叶变换、谱分析、小波变换、模态分解［6-9］等，机器学习方法包括人工神经网络、支持向量机、深度学习［10-13］等。如有学者研究发现，通过对经验小波方法进行改进，可有效提高滚动轴承和齿轮箱故障检测效率［14-15］。徐甜甜等提出了结合变分模态分解与谱峭度法的齿轮故障诊断方法，并验证了方法的有效性［16］。Lin et al. 提出了一种基于变分模态分解和布谷鸟搜索参数优化概率神经网络（PNN）的齿轮箱故障模型，并利用东南大学齿轮箱数据集进行了验证［17］。陈如清等将改进烟花算法与PNN 融合，确定PNN 的参数最优值，从而实现了齿轮箱的故障分类［18］。传统的PNN 与其他神经网络相比，模型网络学习过程简单，学习速度快，并且具有一定的分类准确性和抗噪声能力［14］，但是其关键参数选择主要根据经验确定，从而影响了模型对故障诊断的识别率。因此，如何优化PNN模型平滑因子，提高对齿轮故障的诊断效率，是PNN 应用的关键问题。

1 数学模型原理概述

1.1 主成分分析与数据归一化

主成分分析（PCA）是一种常见的数据降维方法［19］，韩璞、张洪波等分别应用该方法与贝叶斯网络、PNN 网络相结合，进行汽轮机、模拟电路的故障诊断［20-21］。

PCA 方法步骤如下：

（1）输入样本集D={ x1, x2,… , xm}；

（3）计算协方差矩阵XXT及所对应的特征值和特征向量；

（4）按照累计贡献率达到90%确定数据最佳维数d′；

（5）取最佳d′个特征值所对应的特征向量ω1，ω2，…，ωd′，输 出 投 影 矩 阵W*=（ω1，ω2，…，ωd′）。

1.2 概率神经网络

PNN 是一种以贝叶斯和Parzen 窗函数法为数学基础的前馈神经网络，其网络拓扑结构包括输入层、模式层、求和层和输出层，如图1所示。

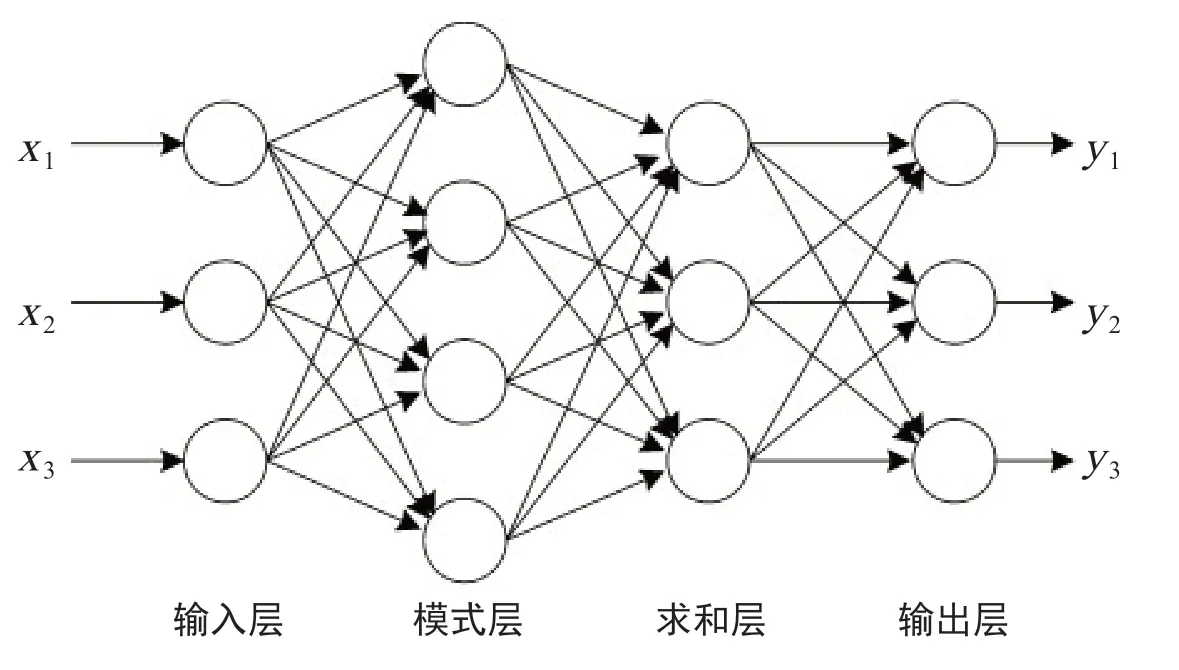
图1 PNN 网络拓扑结构

设有d个网络输入向量，表示为X=［x1，x2，…，xd］T；n个输出向量，表示为Y=［y1，y2，…，yn］T，训练过程如下。

（1）输入层完成训练样本特征向量X 的接收，并将数据向后传递。

（2）模式层采用径向基非线性映射，计算各模式种类与输入向量的匹配度，并将其输出至求和层，该层中第i个类别与第k个神经元所对应的函数为：

式中：i= 1，2，…，d为训练样本特征值个数；ωik为连接模式层和求和层的权值向量；σ为平滑因子，其取值影响着PNN 分类的正确识别率。

（3）求和层把模式层中类别相同的隐含神经元输出，依据Parzen 窗方法得到各类别的概率密度函数估计值，其输出公式为：

式中：fi（x）为第i种标签值的输出；N为第i类神经元的数量。

（4）输出层把从求和层得到的每一类概率密度函数通过竞争神经元做阈值辨别，在所有输出种类中选取出匹配度最高的一个输出，从而完成隶属类别的判定。

1.3 麻雀搜索算法

麻雀搜索算法（SSA）提出于2020 年，主要模拟自然界麻雀寻找食物并躲避猎捕的行为［22］。SSA 把麻雀种群分成发现者、追随者、警戒者三类。发现者的任务是觅食并为整个种群进化提供导向，其数量在整个种群中占比设置为10% ~ 20%。追随者的任务是紧紧跟随在发现者周围进行觅食，发现者和追随者在进化过程中满足进化规则条件时可互换角色。其位置重新计算的公式［23］分别为：

为了种群安全，SSA 会在整个种群中随机选取10% ~ 20%的麻雀作为警戒者，警戒者的任务是作为种群侦察兵，在种群受到外界捕食者威胁时及时提醒其他麻雀［22］。警戒者位置更新公式为：

式中：β为服从标准正态分布的随机数，K∈［-1，1］，η为最小常数，fm为当前适应度值，fg为最佳适应度值，fω为最差适应度值，Xbest为全局最优解。

1.4 PCA-SSA-PNN 故障诊断模型

维度过高的样本数据会增加问题分析的复杂度，并且影响PNN 分类精度。同时，PNN 性能优劣与平滑因子σ选取密切相关，传统做法是根据经验选取，因缺乏理论依据，不能充分发挥PNN的作用，从而使得样本维数较大时PNN 分类器识别率较低。我们的样本数据维数较大，对训练时间和精度影响较大。因此，我们提出采用PCA 方法对数据进行降维，然后利用SSA 对PNN 的平滑因子σ进行优化，形成自适应概率神经网络，改善PNN 的性能以达到最佳的齿轮故障识别率，即PCA-SSA-PNN 故障诊断模型。具体实现流程如下：

（1）将齿轮故障数据导入系统；

（2）利用PCA 进行数据降维；

（3）设置SSA 算法参数，设置种群大小、意识到危险的麻雀数量、最大迭代次数等；

（4）通过公式（4）至（6）迭代计算麻雀种群中各角色位置，并计算在相应位置时的适应度值，以更新全局最优个体；

（5）迭代次数达到最大设定值时，输出全局最优平滑因子σ，将样本数据输入至优化后的模型，并输出齿轮故障诊断结果。

2 齿轮故障诊断实例

2.1 数据来源及齿轮故障特征

案例采用康涅狄格大学齿轮实验平台及其数据集，实验系统及结构如图2 所示［10］。齿轮振动信号由加速度计测量，采样频率为20 kHz。

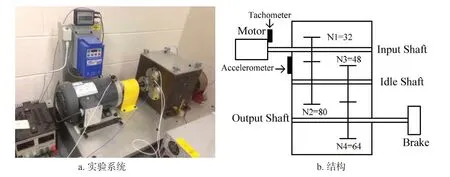
图2 齿轮实验系统及结构

数据集包括两部分：采用时间同步平均处理后的时域齿轮故障数据和角频域同步分析后的频域齿轮故障数据。齿轮故障包括正常（本文将“正常”也视为故障识别的一种结果）、断齿、齿根开裂、剥落、削尖1（最严重）、削尖2、削尖3、削尖4、削尖5（最轻微）。对每种齿轮状态使用实验齿轮箱系统采集104 个信号，一共936 个样本，其中每个样本包含4 个齿轮振动信号的3 600 维角频域数据和3 维时域数据，我们使用的所有数据均在网站https：//doi.org/10.6084/m9.figshare.6127874.v1 上公开。

2.2 模型参数设置

在每组样本中随机选取82 个（共计738 个）样本作为训练集，每组剩下的22 个（共计198个）样本作为测试集。

构建PCA-SSA-PNN 故障诊断模型，对PCA 降维维度，设置不同的维数d'观察主成分的累计贡献率，以得到最佳维数，经测试，当d'=200时累计贡献率为90.6%，因此本文设置d'=200，这样既将数据降维，易于进行故障分类识别，又可减少程序运行时间。降维后数据归一化到0~1 之间，以加快训练网络的收敛性。由于PNN 层数固定，输入层神经元个数与数据维数一致，不需要设计网络层数。我们的样本数据特征原有3 603个，经过PCA 降维后为200 个，因此输入层神经元个数为200。输出层个数对应于齿轮故障状态，故输出层神经元个数定为9。SSA-PNN 网络的其他参数设置如下：种群数量pop＝20，下边界lb＝0.01，上边界ub＝5，适应度函数为为证明PCA-SSA-PNN 网络的有效性，我们同时构建了PNN 模型和PCA-PNN 模型，网络参数设定完成后，通过MATLAB 进行计算。本文所使用的训练环境：CPU 为Intel Core i5_8265U CPU，内存4G。

2.3 PCA-SSA-PNN 模型训练效果

由于SSA 算法最大迭代次数（M）对预测精度和运行时间影响较大，考虑到计算时间，同时为避免陷入局部最优，经测试后设置M为25，适应度寻优曲线如图3 所示。

图3 适应度寻优曲线

由图3 可知，优化后的PCA-SSA-PNN 诊断模型诊断适应度下降很快。在SSA 优化初期，因个体适应度较低，迭代后网络陷入短暂的局部最优，随着种群迭代次数的不断增加，与最优值的差距不断缩小。一般在迭代5 次后网络跳出局部最优，迅速收敛，快速找到PNN 模型的最佳σ。

PCA-SSA-PNN 模型训练结束后，其训练效果和误差如图4 所示，可见其分类训练效果非常好，训练误差为0，说明建立的模型分类识别性能优越。

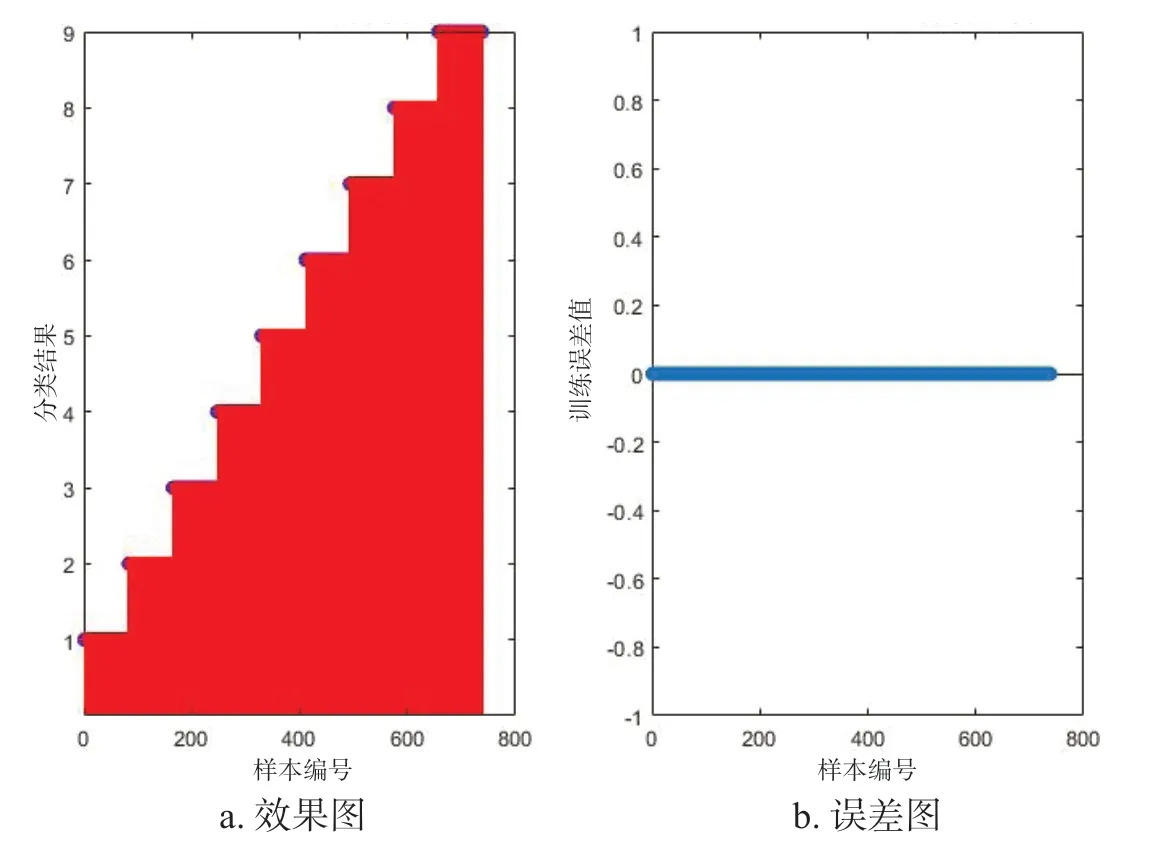
图4 PCA-SSA-PNN 分类训练结果

3 齿轮故障诊断结果分析

3.1 不同模型对齿轮故障分类识别率的影响

由于神经网络运行时存在随机性，因此每种模型均运行8 次进行对比，如表1 所示。

表1 各模型识别率

为加强对比，将表1 中的识别率以图形形式对比（见图5）。

图5 齿轮故障分类识别率对比

由图5 可知，在多次运行中，PCA-SSA-PNN模型的分类正确率均高于其余两个模型。若对所采集的数据不进行任何处理，传统PNN 模型进行故障诊断，其平均识别率仅为74.4%。对数据集基于PCA 方法进行特征提取后，PCA-PNN 模型的平均识别率提升到88.3%。经SSA 优化的PCA-SSAPNN 模型的平均识别率在PCA-PNN 的基础上进一步提高到92.6%，说明了所提出模型的有效性。

每种模型运行时间不同，与标准的PNN 模型相比，优化的PCA-SSA-PNN 比较耗时，平均为93.4s，但在可接受的范围内。若使用计算性能佳的计算机，可有效减少运行时间。

为与PCA-SSA-PNN 故障诊断模型对比，文中同时采用PCA-PNN、PCA-GRNN、PCARBF、PCA-KNN、PNN 模型，训练网络最优后统计8 次运行的平均值，如表2 所示。

表2 六种模型故障诊断识别率 单位：%

由表2 可知，PCA-SSA-PNN 齿轮故障诊断模型诊断结果最佳，优化后的齿轮故障诊断模型正确识别率为92.6%，与PCA-PNN 模型相比故障识别率提高4.3%，且明显高于其他网络模型的识别率。这是因为PCA 方法对数据集有一定的降噪效果，同时，经SSA 优化的PNN 模型能找到最佳的σ，因此故障识别率最佳。

3.2 齿轮故障分类识别可视化结果分析

图6 列出了PNN、PCA-PNN、PCA-SSA-PNN模型8 次运行时最接近平均值的一次可视化诊断结果。

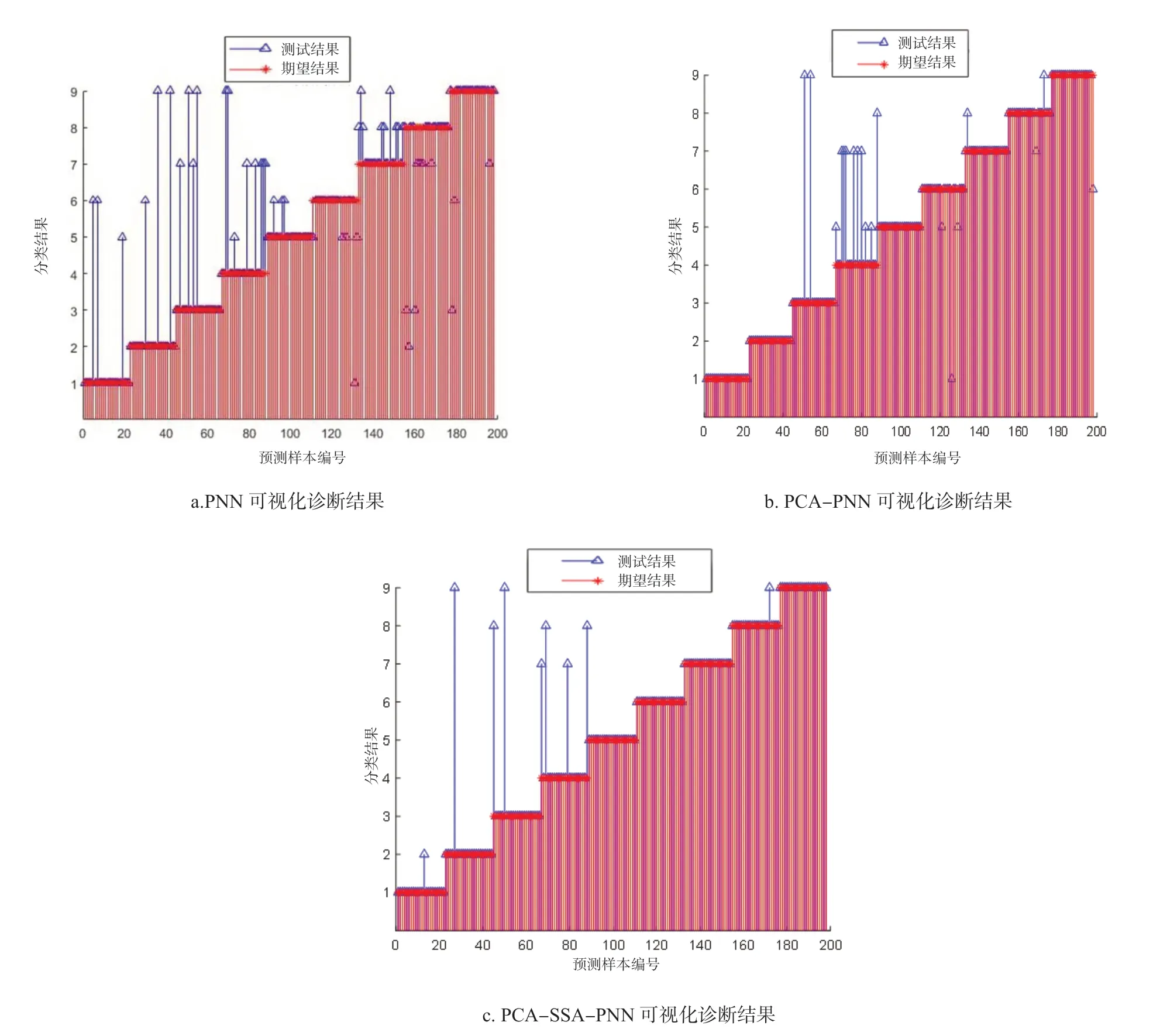
图6 三种模型可视化诊断结果

图6 中，纵坐标1~9 分别对应齿轮正常、断齿、齿根开裂、剥落、削尖1（最严重）、削尖2、削尖3、削尖4、削尖5（最轻微）9 种状态。由图6 可知，PNN 模型错误识别样本明显多于其余两种。PCA-PNN 模型的正确识别率明显提高，即数据经PCA 降维后能有效提升识别率。PCA-SSAPNN 模型的故障诊断正确识别率最高，错误识别样本仅有9 个，可见该模型用于齿轮故障诊断可行度较高。

由于传统PNN 对齿轮故障诊断分类预测效果不佳，后续分析对比仅针对PCA-PNN 和PCASSA-PNN 模型。统计两种模型对齿轮每种故障的识别率，如表3 所示。

表3 两种模型对每种故障的识别率（9 种故障） 单位：%

由表3 可知，PCA-PNN 模型对齿轮各种故障状态正确识别率差别较大，其中正常、断齿、削尖1、削尖4 识别率为100%，齿根开裂和剥落识别率分别为77.2%、59.1%。PCA-SSA-PNN 模型对正常、削尖3、削尖5 的识别率为100%，识别率较低的为剥落和削尖4，分别为77.3%和86.4%。

3.3 样本数量改变对齿轮故障诊断识别率的影响

删除齿轮故障数据集中剥落和齿根开裂的故障样本，以剩余7 种齿轮故障样本基于PCA-PNN和PCA-SSA-PNN 模型按前述步骤重新进行齿轮故障诊断，结果如表4 所示。

表4 齿轮故障诊断识别率（7 种故障） 单位：%

由表4 可知，降低样本集数量后，PCA-PNN模型中识别率较低的故障仍然存在，削尖2 故障识别率由之前的86.3%降为68.1%，削尖4 故障识别率由100%降为86.3%，但总体平均识别率有所提升，达到92.2%。PCA-SSA-PNN 模型的削尖3 故障识别率由100%降为86.3%，削尖5 由100%降为90.9%，总体平均识别率同样提升，达到94.2%。即与之前相比，两种模型诊断正确识别率均有所上升，分别增加了3.9%和1.6%。

3.4 噪声对齿轮故障诊断模型识别率的影响

抗噪能力对齿轮故障诊断模型的性能评价尤为重要，为了测试我们所建立的PCA-SSA-PNN模型的抗噪性能，在数据集中添加随机分布噪声，噪声系数为原有特征的1%、3%、6%、10%。

每种情况运行5 次取平均值，两种模型对齿轮故障分类的识别率如表5 所示。

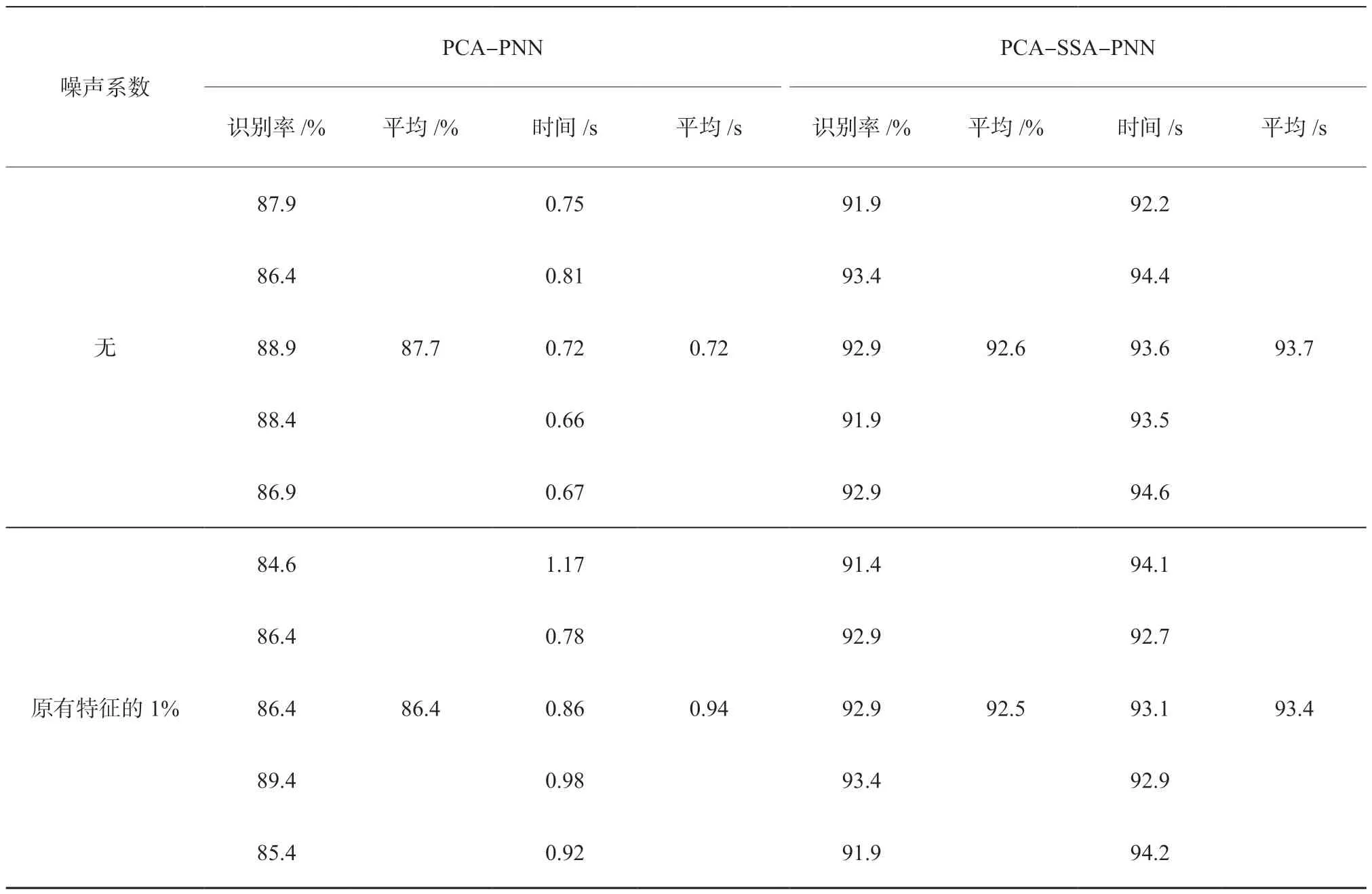
表5 噪声系数改变时故障诊断识别率

由表5 可知，齿轮振动数据集添加随机噪声干扰后，与无噪声相比，两种齿轮故障诊断模型的识别率均有所降低，但噪声程度在10%以下时识别率仍都大于85%，说明均具有一定的抗噪声能力。PCASSA-PNN 模型在噪声系数小于等于3%时，正确识别率基本不变，而未经优化的PCA-PNN 模型，故障识别率下降了2.3%。噪声系数为10%时，PCASSA-PNN 模型齿轮故障识别率为89%。同样噪声系数为10%时，未优化的PCA-PNN 模型齿轮故障识别率下降到85.2%，此时PCA-SSA-PNN 模型故障识别率比PCA-PNN 模型高3.8%。故本文建立的PCA-SSA-PNN 模型在噪声干扰情况下仍具有较高的故障识别率。另外，两种模型的运行时间与噪声系数之间没有明确关系，即有无噪声影响，对程序的运行时间几乎没有影响。

4 结论

我们基于齿轮箱振动信号，对齿轮9 种不同的损伤状态，在根据经验选择PNN 模型平滑因子从而使模型识别率不高的情况下，融合主成分分析法、麻雀搜索算法和PNN 模型，提出一种PCASSA-PNN 模型，用于齿轮箱故障诊断，得出以下结论。

（1）基于PCA 进行数据集降维，引入SSA 优化PNN 模型的平滑因子，建立PCA-SSA-PNN 模型，能有效提升齿轮故障分类的正确识别率，针对齿轮的9 种损伤状态，诊断正确识别率提升到92.6%。

（2）样本数量影响模型正确识别率，文中减少两种齿轮故障的样本数量时PCA-SSA-PNN 模型识别率上升1.6%，达到94.2%。

（3）添加噪声后，模型故障分类识别率有所降低，但在噪声系数为10%时，识别率仍比PCAPNN 模型高3.8%。因此，PCA-SSA-PNN 模型具有较好的抗噪能力。