基于动态角色分配的一致性协同无人机编队控制

姜鸿儒，范云锋，徐亚周，董诗音，赵佳欢

(上海机电工程研究所，上海 201108)

0 引言

随着硬件向微型化、高精度方向快速发展，目前无人机已在军事和民用领得到了广泛地应用，尤其在电子对抗、探测侦察、航空摄影、地质勘定等多个领域占据了一定的使用基础。良好的机动性能、较强的环境适应能力、可观的隐身性能、极高的性价比等一系列优点使得它不但在军事层面有着重大的战略意义，而且在民用领域具有巨大的商业价值。随着无人机的普及，使用者发现在环境复杂的场景下，单一无人机工作能力有限，工作范围也会受到很大限制，致使单一无人机在受到损坏的情况下无法完成目标任务，造成巨大损失，所以多无人机合作协同的需求增加，进而推动了多智能体协同编队控制的研究来弥补单一无人机在执行任务时出现的探索视野存在盲区、作战使用范围受限、区域目标搜索能力差、鲁棒性弱，执行任务周期长等问题。

随着任务难度的提升，无人机协同编队将是未来的军事领域主要发展内容之一。多无人机的协同控制可以很好地弥补单一无人机在执行任务中出现的作战半径有限、巡航时间短、视野残缺、容错率低、鲁棒性差等问题，并且多无人机协同可将任务细化，给不同类型的无人机分配角色，让其各自完成自身较为擅长的子任务，从而提升整体的作战能力和任务完成率。其中，让多无人机可以保持原定队形进行运动，并在突发情况下仍能根据当前环境和自身情况找到适合的编队位置是无人机协同编队的重点和难点，也是目前迫切需要解决的无人机编队问题之一。

在无人机的姿态控制的基础上，美国各高校率先对多无人机编队控制进行研究。宾夕法尼亚大学GRASP实验室通过动作捕捉系统获取各个无人机的位置信息，完成了多架无人机的躲避障碍和编队飞行任务[1]，并在TED上展示了展示了他们的研究成果[2]，使得无人机编队控制得到了更高的关注。麻省理工大学选择了另一种编队方式，通过利用无人机搭载的惯导器件和其他传感器来获取自身的姿态信息和周围环境信息，进而实现轨迹规划，完成目标搜索等任务[3]。伯克利大学的bear实验室设计了非线性模型预测控制方法对多智能体进行便对控制[4]等。

相对国外，国内无人机虽起步晚但发展较快，在编队控制问题上都有了很大的突破和进展[5]。基于一致性算法研究“领航者―跟随者”策略[6]。设计了基于三阶一致性理论设计编队控制器解决某无人机无法工作的情况下其它无人机仍保持队形稳定飞行的问题[7]。基于位置误差和同步误差的同步控制算法来实现对四旋翼无人机的编队控制。在收到干扰的情况下[8]，设计了一种基于信息交互的一致性编队控制方法和基于协同航迹规划和跟踪的编队控制的双模式切换的无人机编队控制方法，来增强编队的抗干扰能力[9]。基于自适应积分滑模控制框架，设计了一种无人机编队控制器方法[10]。利用观测器来对干扰进行补偿，设计了一种基于状态观测器的分布式有限时间编队跟踪控制策略[11]。根据无人机的特点、飞行情况，对一致性变量的边界问题进行平滑设计以及限幅处理，设计了一种改进的一致性编队控制算法，提高了编队控制算法的控制效果和执行效率[12]。提出了一种将基于行为法和虚拟领航者法相结合的混合编队技术编队，设计了奔向目标、队形保持、避碰及避障共4种基本行为解决无人机群体在复杂战场环境下的编队、避障、避碰问题。除此之外，随着人工智能算法领域的发展，一些神经网络、博弈论等算法也被运用在编队控制算法中[13]。提出一种基于博弈的分布式控制算法，利用一致性方法和梯度下降实现纳什均衡点的求解从而实现理想编队[14]。设计了一种新的BP神经网络辅助的自适应PID无人机编队智能控制算法，提高了现有PID算法的计算精度[15]。设计了一种多四旋翼分布式神经自适应动态面协同编队控制方法，实现对四旋翼位置回路和角度回路未知非线性干扰的快速平滑学习与补偿[16]。设计了基于深度强化学习中DDQN算法设计无人机编队控制器，控制速度与航向通道，使僚机能够自学习跟踪长机并保持编队。这些算法对无人机的硬件要求较为苛刻且计算量较大，在实际执行任务中较难实现。此外，大多数算法未考虑无人机编队整体能耗的影响，可能会导致执行任务范围大大缩小，降低其实际的应用价值。

本文的贡献在于在控制多无人机编队的同时考虑了实际复杂环境和无人机整体编队的能量损耗问题，设计了一种基于动态角色分配的一致性协同无人机编队控制方法。无人机获得各自编队中的角色，再得到其他无人机的位置信息和队形信息后通过匈牙利算法得到最优分配并动态更新各自角色信息和位置信息，使多无人机收敛到一致性轨迹跟踪控制下的队形位置，并对相关算法进行了证明。在此基础之上，以5架无人机为例通过仿真实验对所设计的编队方法进行了验证。

本文接下来将从以下几方面进行介绍：第1节将简单介绍无人机的运动学模型及相应的基于扩张状态观测器的反馈线性化姿态控制器；第2节将首先介绍一些的图论知识为后续控制算法设计和证明做支撑，然后介绍所设计的一致性编队控制算法和基于匈牙利算法的动态角色分配模型，并给出相应的理论证明；第3节将以5架无人机为例进行实验仿真并分析仿真结果；最后，在第4节中给出了相应研究结论。

1 无人机运动学模型及姿态控制方法

本节介绍一下，无人机的运动学模型以及其相应的姿态控制算法，为多无人机编队提供基础。本文采用的无人机运动学模型为通用的无人机运动学模型，设计的姿态控制方法为基于扩张状态观测器的反馈线性化姿态控制器。

1.1 运动学模型

我们采用通用的无人机的姿态动力学和运动学模型，如下所示[17]：

其中：χ和γ表示无人机的航向角和航迹角。δ，τ，ΩE分别表示纬度、经度和地球的角速度。α，β，μ分别表示攻角、侧滑角和倾斜角。p，q，r表示无人机的体坐标系。Mx，My，Mz表示攻角，侧滑，倾斜角的气动力矩。f1，f2，f3表示额外干扰。Ixx，Iyy，Izz分别表示机体围绕X，Y，Z轴的转动惯量。

为了从状态过程中分离控制器，以及设置有空气动力学参数的不确定性和其他因素所造成的扰动。从模型中可以看出，由于无人机在飞行过程中姿态角相较于姿态角速度的变化速度慢，往往两者间会差几个数量级，由此可以将姿态角速度和姿态角度两者剥离开来，对两者分别进行控制，因此可以将上式看成两个子系统，分别为状态变量为Ω的角度子系统和状态变量为ω的角速度子系统。

通过简化，可得：

其中：

1.2 姿态控制方法

根据简化的无人机运动学模型，设计了反馈线性化姿态控制方法，并利用扩张状态观测器对扰动进行精确估计和补偿。具体控制器如下，

角度子系统控制器：

其中：k=diag(kα，kβ，kμ)，kα，kβ，kμ都是正常数，用于调节姿态子系统的误差，以此来让系统为渐近稳定。

角速度子系统控制器：

其中：u是反馈控制量，kf=diag{k1，k2，k3}，e=ωc-ω。

角速度子系统扩张状态观测器：

具体的稳定性分析可参考[18]。该方法减少调节参数，大大降低了调节难度，同时利用扩张状态观测器来对扰动进行估计和补偿，提高了无人机姿态控制的精度。

2 编队控制

在上一节无人机姿态控制的基础上，进行多无人机编队控制器的设计。考虑到在实际执行任务时，存在复杂的地理环境飞行损耗、巡航周期和固定能量等能耗问题，本节设计了一种在多无人机执行任务过程中可依据具体的周围环境情况来重新制定编队方案和重新分配各无人机角色、确定自身位置以此来缩小执行任务周期，同时减小整体行径航路和能量消耗的基于动态角色分配的一致性编队控制方法。

以每个无人机知悉周围无人机位置信息和编队信息为前提，通过设计的多无人机编队方法可动态更新每个无人机在编队中的角色和位置，通过匈牙利算法[19]得到最优分配，使得每个无人机收敛到一致性轨迹跟踪控制下的队形位置。在设计编队控制器前，需要介绍一些编队控制的一些基础的图论知识，便于更好的理解无人机编队控制算法。

2.1 基础知识

2.1.1 图论知识

假设一个编队中由n个节点组成，图g是由非空顶点集V= {1，2，…，n}和边集ε⊆V×V组成[20]。在有向图中，边集中的边(i，j)表示节点j可获得节点i的信息，但反之则不一定成立。而在无向图中，边集中的边(i，j)表示节点i和节点j可相互通信得到彼此信息。若存在一个有向树包含图g中所有的点，则称其为有向生成树。有向图包含有向生成树，即有向生成树为有向图的一个子集，则至少存在一个点可通过有向路径指向图中所有其他节点。存在一种特殊情况，若图中任意两个节点间都有边，则称之为完全图。

An=[aij]⊆n×n是图g的加权邻接矩阵，若aij⊆ε，则定义aij>0，否则aij=0。对于无向图来说，加权邻接矩阵是对称矩阵，即aij=aji。

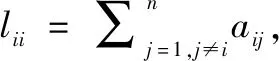
2.1.2 匈牙利算法

匈牙利算法主要是根据二部图匹配将最大流算法进行了简化，通过寻找增广路径以此来求得二分图最大匹配的算法，提高了整体的计算效率。普通的最大流算法一般都是基于带权网络模型的，二部图匹配问题不需要区分图中的源点和汇点，也不关心边的方向，因此不需要复杂的网络图模型。具体内容如下。

1)寻找代价矩阵中所有行中最小的元素，并减掉该行的最小元素，同理，找到所有列中的最小元素并在该列中减掉，使代价函数每一行每一列都有零元素；

2)n阶的代价矩阵需至少有n个独立的零元素，然后将这些独立的零元素设为1，其他的元素都设为0，进而得到代价矩阵的最优解。但可以得到n个独立零元素的情况比较少见，如果无法获得n个独立零元素，需要从只有一个零元素的行(列)中进行标记，将该列(行)中的其他零元素划掉以表示此任务指派于他而其他节点不能完成该任务。如此反复，直到所有零元素都做了相应的标记。若所标记出的零的个数为n个，则表示该代价矩阵得到最优解，否则进行步骤3)；

3)为使代价矩阵能找到最多的独立零元素，即选择最少的直线来覆盖代价矩阵中的所有零元素。做如下操作，对没有标记的行打勾，对已打勾的行中有划掉零的列打勾，再对打勾的列中含标记的行打勾，重复进行上述步骤直到不能再打勾为止。对未打勾的行和列画线，即可得到用最少的直线覆盖所有零元素；

4)从代价矩阵中找到未被直线覆盖的元素中的最小元素，并对每个未被直线覆盖的元素减掉该最小元素，对被直线覆盖的元素加该最小元素，得到一个新的矩阵，再开始从第2步重复进行，直到圈出的零元素等于n为止，则找到最优匹配。

2.2 一致性编队控制算法

由于图g是由一个无人机(领航者)和n个无人机共同组成。

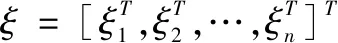
(1)

其中：ui，i=1，2…，n为给定协议，若存在一个平衡点ξ*使得当t→ ∞下，针对任何初始状态都可令ξ→ξ*，则说明了每个智能体能收敛于原定队形或拓扑中。

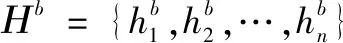
假设1：图g是完全图。

针对每个智能体，其编队的一致性轨迹跟踪算法为

(2)

其中：kij，αi为调节参数。

定理 2.2.1：如上文定义A=[aij]⊆(n+1)×(n+1)，aij和ai(n+1)有信息交流时为1，否则为0，a(n+1)k=0，∀k⊆{1，2，…，n}。 当且仅当A为有向图和ai(n+1)=1时，ξi→ξr+hi，ξj→ξr+hj。

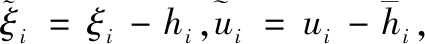
(3)

根据式(2)～(3)，得

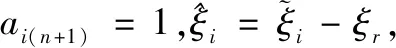
其中：Ln=[lij]⊆n×n且lij=-aijkij(i≠j)，lii=∑i≠jaijkij，∀i，j∈{1，2，…，n}，

2.3 动态角色分配

基于一致性编队控制算法，本小节考虑多无人机在执行任务中的能耗问题。通过采用匈牙利算法来进行对编队无人机的动态角色分配，使得多无人机在遇到复杂环境时根据自身位置和编队信息进行角色转换，从而减少各无人机因维持编队位置的飞行航程，大大的降低了整体编队的飞行能耗。该方法是为给定的代价矩阵找到最优分配的算法。

假设2：将智能体分配到最近的目标位置可以最大限度地降低其能源成本[21]。

首先要选择一个合适的代价矩阵。设计代价函数为：

定义代价矩阵如下：

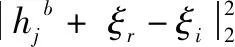
其中：1≤ji≤n，j1≠j2≠…≠jn，即每个ji，i=1，2，…，n相互不在同一行和同一列。

通过选择一组合适的来最大限度地降低成本。组合的选择可通过匈牙利算法得到。

定理 2.3.1：定义矩阵Qn=[qij]⊆n×n，其中若第i个无人机可获得第j个无人机的信息，则qij，反之qij=0。令Hm(t)=[h1(t)，h2(t)，…，hn(t)]，Hm(t)为Ηb元素组成的集合。Hm(t)和Ηb分别为Η(t)和Ηb集合的矩阵形式。令Hm(t)=HbQnT，可有最低成本函数。

证明：

根据Qn所给出的定义，可得如果第i个无人机可得到编队第i个无人机的位置信息，则Qn=In，例如Hm(t)=Hb。通过有限次列变换，可由单位矩阵In导出Qn，使得Qn-1=QnT。所以若Qn≠In，只需将In对Hb做反向转换即可。因此，Hm(t)=HbQnT。

3 仿真结果与分析

针对上述所设计的编队算法和最优分配方法，通过实验仿真来验证基于动态角色分配的一致性协同无人机编队控制方法的可行性和有效性。此次仿真采用5架无人机组成，以1架为领航者，4架为跟随者的编队形式进行实验，主要分为以下两部分内容：

1)验证一致性编队控制算法的可行性。基于“领航者-跟随者”模式，使各无人机实时获取自身位置信息，并各自计算下一时刻的理想位置信息，以此来保持整体编队队形统一，进而验证编队方法的可行性和有效性；

2)验证动态角色分配算法的有效性，使得多无人机在遇到复杂环境时根据自身位置和编队信息进行角色转换，减少各无人机因维持编队位置的飞行航程，大大的降低整体编队的飞行能耗。实验仿真基于“领航者-跟随者”模式，首先确定4架跟随者无人机的角色，在整体编队飞行过程中，通过改动编队中其中2架跟随者节点的相对初始位置，来观察整体编队中各个节点的飞行轨迹，是否降低了整体编队的飞行能耗，以此来验证动态动态角色分配的有效性。

所设计的一致性编队控制算法，控制器的参数如下所示。

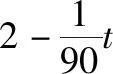
图1 智能体编队

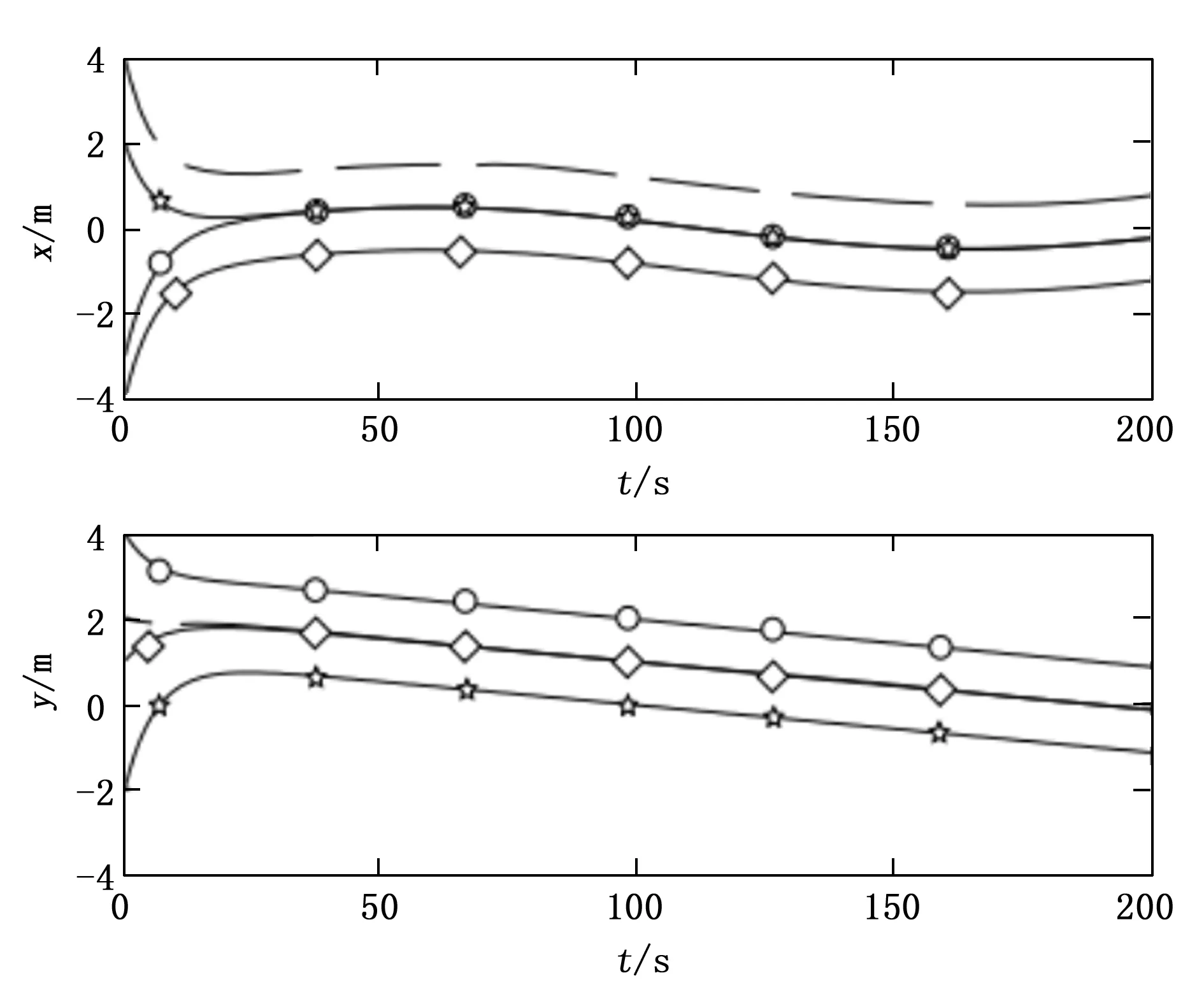
图2 xy轴跟踪情况

接下来，验证动态角色分配算法的有效性。为了进一步验证该编队控制方法具备根据环境来降低整体耗能的能力，在原有队形的基础之上，对其中跟随者的位置进行整体修改，将整体的队形进行180°旋转。

图3为未加入匈牙利算法的一致性编队控制的仿真结果，图4为加入有匈牙利算法的仿真结果。从仿真结果可以看出，未加入动态角色分配算法的编队控制，4个跟随者会根据自身原有的角色按照原来角色的编队理想位置进行移动，大大增加了飞行航程，同时也增加各跟随者在飞行过程中碰撞的风险。而加入动态角色分配算法的编队控制器可以根据环境的变化来更改编队中跟随者的自身身份，从仿真结果中可以看到，4个跟随者在执行任务过程中，1号身份无人机转变为4号身份无人机，2号身份无人机转变为3号身份无人机，3号身份无人机转变为1号身份无人机和4号身份无人机转变为2号身份无人机，使得多无人机在执行任务中减少了整体的行驶路径，从而降低了整体的能源成本，降低了碰撞的风险，大大提高了其实际的应用价值。可以看出通过使用动态角色分配算法可以减少整体编队的飞行航迹，降低能源成本。

图3 改变位置编队(无匈牙利算法)

图4 改变位置编队(有匈牙利算法)

4 结束语

针对多无人机在飞行过程中编队保持快速收敛和复杂环境下队形保持的相关能耗问题，本文设计了一种基于动态角色分配的一致性协同无人机编队控制方法来控制“领航者-跟随者”模式下多无人机的编队位置及动态分配跟随者各自身份。本文所设计的一致性编队控制算法，可以提升编队中各无人机的编队位置精度，缩短收敛时间和提高编队系统整体的鲁棒性。除此之外，本文在编队控制器中加入基于匈牙利算法的动态角色分配方法使多无人机在执行任务过程中可依据具体的周围环境情况来重新制定编队方案动态分配跟随者的角色信息，使得跟随者根据新角色快速收敛到最优的编队位置以此来缩小整体的编队飞行轨迹和任务执行周期，减小整体能量消耗，并以5架无人机(1架领航者，4架跟随者)构成编队为例开展了编队飞行仿真分析，仿真结果也进一步证明了本文所设计的一种基于动态角色分配的一致性协同无人机编队控制算法的可行性和有效性。

综上所述，可以得出本文设计出的基于动态角色分配的一致性协同无人机编队控制算法能够很好的对多个无人机进行编队控制，提升编队中各无人机的编队位置精度，缩短收敛时间和提高编队系统整体的鲁棒性，同时通过动态角色分配算法重新分配各个跟随者的角色使其获得编队中最佳的预期理想位置，从而减少了各节点的行驶路径，降低了编队飞行中的整体能源成本。