突显函数单调性的示范作用 发展学生数学核心素养
广西南宁市第三中学 (530021) 邹信武
1 问题的提出
函数单调性是反映函数变化规律的一个基本性质,由于它的“抽象性”和“应用性”,历来都是高中数学教师研究的重点教学内容.在以往的教学设计中,重点往往在于如何引导学生理解“符号化表示”和“任意性”上,诚然,这是学生学习函数单调性时的认知障碍,但是,从发展数学核心素养的角度,函数单调性还承载着更多的教育教学作用.
2 函数单调性教学作用
2.1 函数单调性是发展数学核心素养的优良载体
函数单调性是发展学生数学核心素养的良好教学素材.函数单调性概念的形成中,学生经历了从图形语言、自然语言再到符号语言表达的过程,从具体到一般,从“定性分析”到“定量刻画”,可以发展学生数学抽象素养;在经历具体函数图象的单调性提炼和函数单调性在具体函数的“直观图象”中,发展学生直观想象素养;在理解函数单调性概念中的“全称量词”、“特称量词”等逻辑用语中,发展学生逻辑推理素养;在利用函数单调性定义解决具体问题中,发展学生数学运算等素养.
2.2 函数单调性是后续学习函数性质的优良“示范”
学生在学习函数概念和函数的表示方法之后,在学生心中可以产生大量的问题,如下一步应该学习(思考)函数的什么呢?什么是函数的性质?如何寻找函数的性质?又应该表达它们呢?这样做有什么作用呢?……这些问题恰恰利于发展学生的“理性思维”.因此,应该把握住这一教学契机,在函数单调性的探求过程中,引导学生逐步明了研究函数性质的基本框架和路径,使数学中发展特有的目标取向、思考结构、思维方式和符号化表达有机的融入系列化数学活动中,形成一个完整的数学研究过程,为后续函数性质研究提供一个“示范”.
3 函数单调性的学习过程
函数的单调性概念的形式化过程,本质上就是数学概念的抽象过程.关于数学抽象,史宁中教授将它分成三个阶段:一是简约阶段,即抓住事物特征,语言表达;二是符号阶段,即抓住事物本质,符号表达;三是普适阶段,即抓住事物关联,模型表达.函数单调性的教学过程应尊重数学抽象的层次性,兼顾学生思维的发展水平,概念形成与概念同化相结合.如图1,将函数单调性的概念学习分为四个阶段:方法与途径、辨别与提炼、表征与定义、完备与应用.
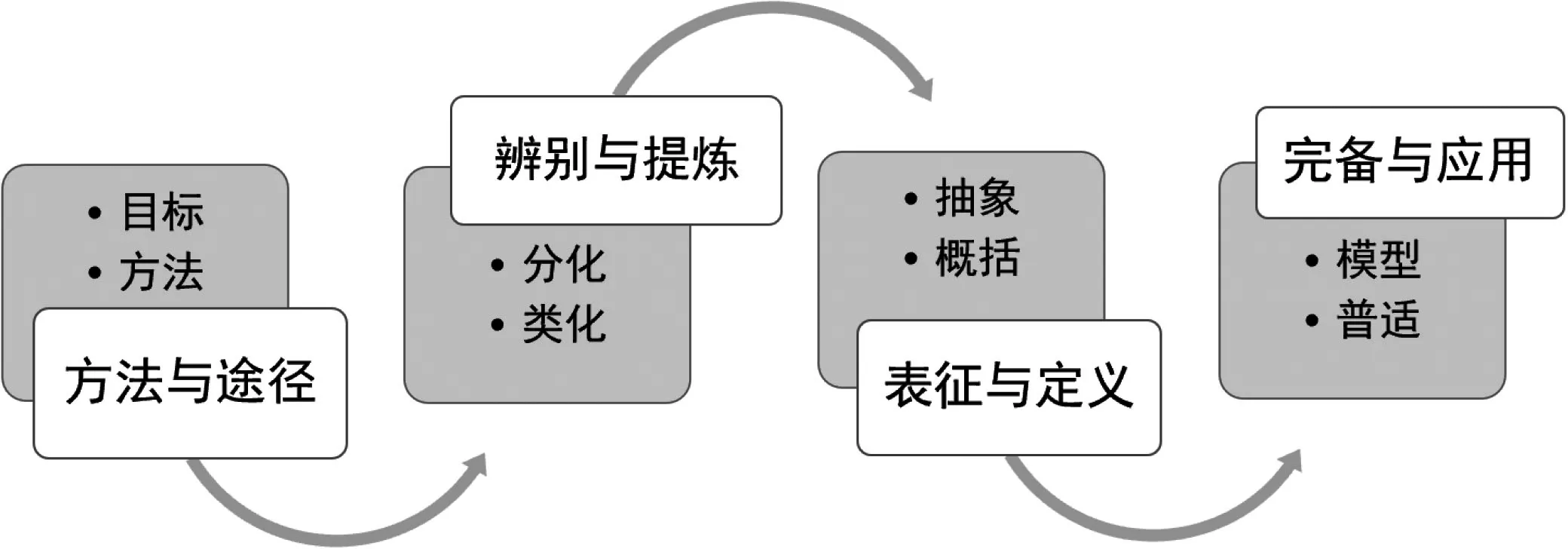
图1 函数-单调性学习过程
4 函数单调性教学设计
4.1 方法与途径
引入:前面我们学习了函数的定义和表示法,知道函数是描述客观世界中变量之间的一种对应关系.这样,我们就可以通过研究函数的变量间的变化规律来把握客观世界中事物的间的变化规律,变化中的不变性就是性质,变化中的规律性也是性质.因此,研究函数的性质,就是研究自变量在变化时,函数值呈现出什么样的变化规律.那么,哪一种函数表示方法可以直观的反映规律性呢?
设计意图:承前启后,交代清楚性质和函数性质的涵义.引出了本节课的主题——研究函数的性质,同时指出了研究的途径:寻找自变量与函数值的变化规律;并且指出研究的出发点:函数的图象.
4.2 辨别与提炼
问题1观察图2中的三个函数图象,你能说说它们分别反映了相应函数的哪些性质吗?哪些是三个函数图象共有的性质?
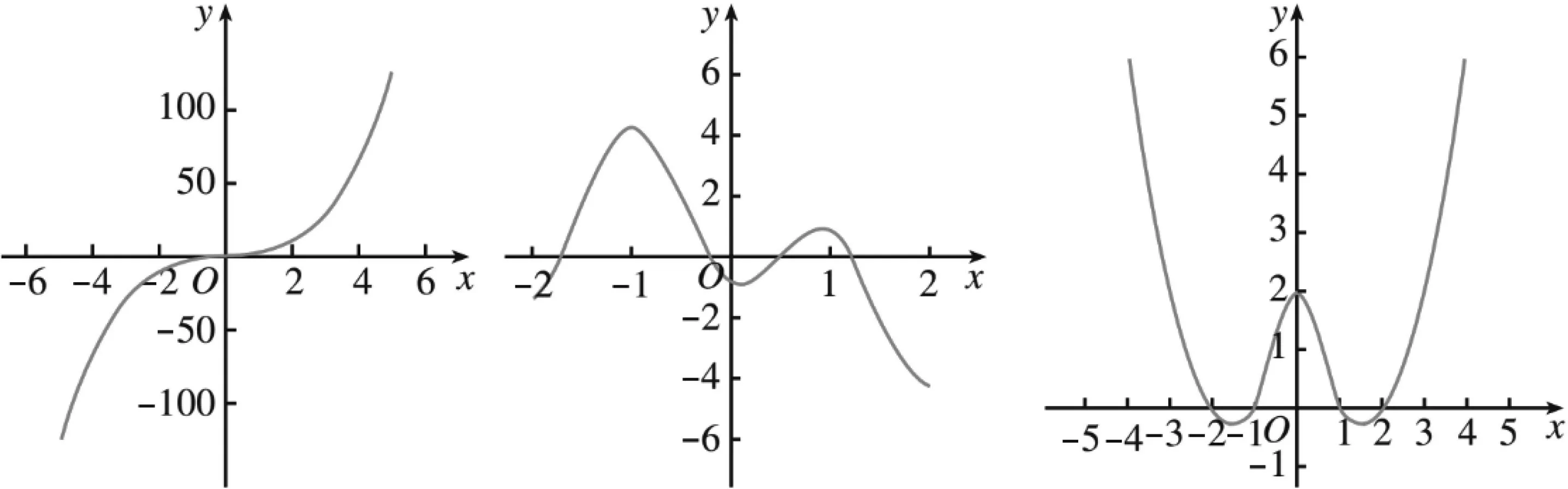
图2
设计意图:这样的处理,既体现了数学抽象中“简约阶段”的特征,又能统摄后续学习内容,体现“大单元”教学观.学生从特殊的三个函数图象中,分析变化规律,并进一步对它们进行提炼和类化,进而得到某些“规律性特征”.这几个图象中,有“上升”、“下降”——单调性,有中心对称和轴对称——奇偶性,有极值和最值,还有变化快慢等特征,这些都是今后要研究的性质.当学生提炼了种种性质之后,再指出“上升”、“下降”这样的图形特征我们称为函数的单调性,本节课的目标就是准确的描述这样的图象特征.
4.3 表征与定义
问题2 我们从简单的函数开始,先研究函数f(x)=x2,g(x)=x3的单调性.请同学们用描点法画出它的图象,并描述出它的单调性情况.
设计意图:这是本节课的关键问题,设计主要从以下几个方面考虑:
(1)从简单到复杂,从特殊到一般,是我们研究问题的一种常见方法.利用特殊函数的图象引导学生进一步明晰单调性的图形直观,并得出图形直观描述:从左往右看,y=g(x)图象在“上升”;当x<0时,y=f(x)图象“下降”,当x>0时,y=f(x)图象“上升”.
(2)此处要求学生使用描点法作图,使学生在列表描点过程中,能直接感受自变量变化时函数值的变化规律,并且把这样的规律与图象变化建立联系,进而实现图象描述向代数刻画转变.
(3)选择f(x)=x2和g(x)=x3的原因还有两个:一是通过对比,让学生体会单调性是函数的局部性质,并且具有普遍性;二是为后面函数奇偶性的研究埋下伏笔.
追问1:函数是自变量与因变量的一种对应关系,对于f(x)=x2,你能用自变量x与函数值f(x)描述刚刚大家得到的函数图象的“上升”和 “下降”吗?
设计意图:学生经历了描点法作图过程,就不难从图形描述转向数学描述性语言:当x<0时,f(x)越小;当x>0时,x越大,f(x)越大.值得注意的是,虽然这样的描述语言在初中已经出现,但是在以往教学实践中,大部分学生依然不能精确地表述,因此这样的复习还是有必要的.
追问2:结合绘制f(x)=x2的过程,请你举例说明:当x>0时,x越大,f(x)越大.
设计意图:函数单调性概念符号化过程中的一个难点就是如何让学生自然地使用区间上两点坐标去刻画变化规律.在这个问题解决过程中,从一般到特殊,随着学生不断列举实例(如1<2,则f(1) 追问3:大家发现了“上升”部分两点间存在大小关系,你能用刚才的发现来描述“当x>0时,x越大,f(x)越大”吗? 设计意图:从特殊到一般,引导学生用符号语言描述“上升”这一性质.这是达成抽象概念的重要过程,虽然描述不完善,但是描述脱离了图象,完成了定性刻画向定量刻画的转变. 追问4:请同学们判断:当x1,x2∈[0,+∞),如果x1 设计意图:引导学生逆向思考,完成函数单调性概念形成过程中的“完备性”.此处是本节课的难点之一,通过设置充分必要条件的判断,使学生意识到“所有点都应满足”,进而体会x1、x2任意性的重要性. 追问5:请同学们用准确的语言刻画f(x)=x2“上升”和“下降”的情况.对于g(x)=x3呢? 设计意图:通过前面的层层铺垫,达成数学抽象符号化.学生在使用严谨的符号语言刻画f(x)=x2的g(x)=x3的单调性情况,体会符号语言的精炼与准确. 追问6:对于函数h(x)=|x|又有怎样的单调性呢?你能描述出来吗? 设计意图:再通过一个特殊函数单调性的判断,深化符号语言表达与理解.让学生再一次体会“图形语言→自然语言→符号语言”这一数学抽象的过程. 问题3如图3,对于一般的函数,你能写出这两种情况的定义. 图3 设计意图:师生一起归纳单调递增(减)、增(减)函数的定义和单调区间的定义.关注学生符号语言的准确性,特别是在区间、任意、取点等地方的细节. 问题4教材中的思考: (1)设A是区间D上某些自变量的值组成的集合,而且?x1,x2∈A,当x1 (2)函数的单调性是对定义域内某个区间而言的,你还能举出在整个定义域内是单调递增的函数例子吗?你能举出在定义域内的某些区间上单调递增但在另一些区间上单调递减的函数例子吗? 设计意图:这是概念同化的过程.因为函数单调性概念的抽象性,可以提供几个问题给学生辨析,增强学生对概念的理解.教材中的两个问题分别从函数单调性中的“任意性”和区间两个方面进一步深化对函数单调性概念的理解. 问题5 例1:根据定义,研究函数f(x)=kx+b(k≠0)的单调性. 设计意图:通过实例使学生体会单调性符号化定义的必要性和实用性,通过例1、例2归纳用单调性定义证明单调性的步骤,例3则是定义法证明单调性的推广和应用. 例1和例2本质上分别是一次函数和反比例函数单调性的判断,在初中我们一般采用图象法进行判断单调性,这样判断的弊端是图像往往只能得到局部的特征,对于“无穷”位置,是无法解释的.因此,引导学生使用定义法证明几个简单函数的单调性,有助于提升代数证明、推理能力,同时也有助于学生理解“无穷”的含义,体会“无穷”的数学处理方法,从中感受数学的美和力量. 例3则是通过一个学生相对陌生的函数,引导学生通过数学运算,进行恰当的变形,进而判断函数单调性,使学生体会定义法判断单调性的强大作用和价值. 问题6请同学们思考并回答以下问题: (1)什么叫函数的单调性?你能举出一些具体例子吗? (2)你认为在理解函数的单调性时应把握好哪些关键问题? (3)利用定义证明单调性的步骤是什么?有哪些注意事项? (4)结合本节课的学习过程,你对函数性质的研究内容和方法有什么体会? 设计意图:通过问题设置,将本节课的知识、方法、技能、过程等进行回顾与提炼,突出函数单调性的概念内涵和外延,归纳函数性质的研究过程,为后续函数性质研究的埋下铺垫. 通过函数单调性教学,我们希望给学生建立一种研究函数性质的“示范”,在这样的“示范”下,后续性质的教学就变成有目的、有方法、有路径的探究学习.学生在学习过程中,得到的不仅仅是函数性质本身,还有探寻和研究问题的思维不断得到锻炼和提升,进而达到“教会学生学习”的教学效果,最终发展学生数学核心素养.
4.4 完备与应用
5 小结

