不同刚度弹性支撑下风力发电机振动响应特性研究

张长春，王 潇，陈建鹏，白聪儿，贾季涛，余清清

(浙江运达风电股份有限公司，浙江省风力发电技术重点实验室，杭州 310012)

0 引言

在全球能源危机和气候变暖的大趋势下，中国提出了碳达峰、碳中和战略目标，清洁能源迎来了跨越式发展；自2021年起的未来5～10年内，风电、光伏发电的年新增装机容量之和将达到1亿kW以上[1]，成为新增能源消费的主体。在风电行业，风电机组是将风能转化为电能的主要装备，而风力发电机是其核心部件之一，其运行状况将直接影响风电机组的使用寿命[2-3]。其中，风力发电机振动问题会引起传动链零部件失效和被破坏[4-5]，造成风电机组故障停机甚至引发安全事故。目前，弹性支撑是风力发电机唯一的减振部件，因此不同刚度的弹性支撑下风力发电机的振动响应特性研究具有重大工程意义[6-8]。

国内外专家针对风力发电机振动问题一直都有研究。刘建勋等[9]研究了减振器与双馈式风力发电机振动的匹配问题；陈纪军等[10]对1.5 MW双馈风力发电机进行模态分析，研究了机座对风力发电机振动响应的影响；Helsen等[11]考虑弹性支撑的影响，将其加入到传动链部件的建模过程，并分析了传动链部件的模态特性；程荣等[12]对风力发电机弹性支撑进行了有限元分析；成臻等[13]基于机械振动学理论，建立发电机弹性支撑系统数学模型和动力学方程，对发电机弹性支撑的减振特性进行设计研究；温斌等[14]在双馈风电机组设计初期，基于ADAMS进行了模态分析，仿真计算出风力发电机运行时可能出现的共振转速区域；晏红文等[15]通过有限元的方法对风力发电机振动问题进行了分析和控制研究；陆超等[16]基于ADAMS建立某一刚度弹性支撑下风力发电机的仿真模型，并通过机组试验数据验证了仿真模型的有效性。

本文针对4、7、15 kN/mm这3种刚度的弹性支撑的风力发电机，利用加速度传感器对风力发电机的驱动端和非驱动端的水平、垂直和轴向的振动响应特性进行实验研究，并利用频谱云图分析风力发电机驱动端和非驱动端在垂直方向的振动响应下的表现。

1 风力发电机振动原理

风力发电机底部通过4个弹性支撑与机座联接，风力发电机驱动端通过联轴器与齿轮箱高速轴输出端相连，进而获得转动力矩。风力发电机和4个弹性支撑可简化成如图1所示的结构模型。图中：x轴表示轴向方向；y轴表示水平方向；z轴表示垂直方向；kx、ky、kz分别为弹性支撑3个方向的刚度；a、b、h分别为x、y、z这3个方向上的重心位置。

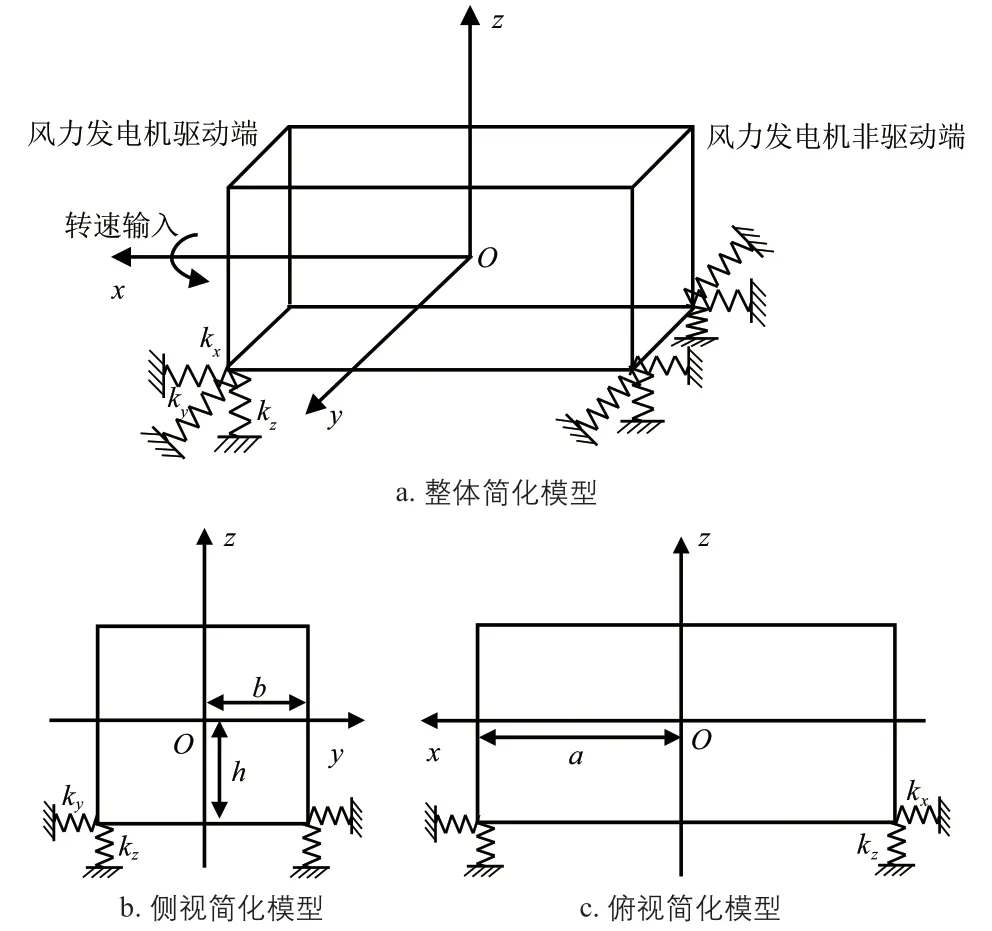
图1 风力发电机和4个弹性支撑的简化模型Fig. 1 Simplified model of wind turbine generator and four elastic support

由于风力发电机属于旋转机械，其所受荷载引起的振动方向主要是沿x轴、y轴和z轴的直线振动，以及绕x轴的扭转振动，这4个方向的固有频率[7]计算公式如下：

沿x轴直线振动的固有频率ωx的计算式为：

式中：Ixx为绕x轴的转动惯量；ωy为沿y轴直线振动的固有频率；m为风力发电机的质量；ωθx为与x轴相关的固有角频率。

其中：

式中：bi为第i阶模态对应的y方向上的重心位置，i=1,2,3…。

沿y轴直线振动的固有频率的计算式为：

式中：Iyy为绕y轴的转动惯量；ωθy为与y轴相关的固有角频率。

其中：

式中：ai为第i阶模态对应的x方向上的重心位置。

沿z轴直线振动的固有频率ωz的计算式为：

绕x轴扭转振动的固有频率ωxx的计算式为：

在风电机组实际运行过程中，通过式(1)～式(7)计算得到4个方向的固有频率，其对应的振动能量主要作用于风力发电机驱动端和非驱动端轴承上，这也使风力发电机轴承成为风电机组故障率最高的部件之一。因此，下文将针对发电机驱动端和非驱动端轴承处的水平、垂直和轴向的振动响应特性进行实验研究。

2 仿真计算

基于风力发电机振动原理，利用动力学仿真软件Recurdyn对发电机转子、发电机外壳体、弹性支撑和轴承进行建模，其动力学模型如图2所示。

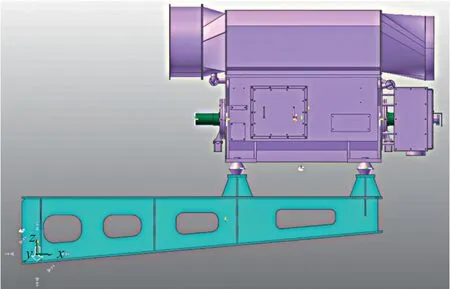
图2 风力发电机的动力学模型Fig. 2 Dynamic model of wind turbine generator

针对4、7、15 kN/mm这3种刚度的弹性支撑，需为发电机转子和外壳体的质量、惯量参数选择合适的参数数值，即：发电机外壳体质量取4685 kg，发电机转子质量取2296 kg，发电机外壳体绕x轴的转动惯量Ixx1取1282 kg·m2，发电机转子绕x轴的转动惯量Ixx2取96.87 kg·m2。

通过仿真计算得到风力发电机在4、7、15 kN/mm这3种刚度的弹性支撑作用下的前5阶振动模态对应的固有频率，具体如表1所示。

表1 不同刚度的弹性支撑下风力发电机前5阶振动模态对应的固有频率Table 1 Natural frequencies corresponding to first five vibration modes of wind turbine generator under elastic support with different stiffness (单位：Hz)

3 风电机组装配厂内的实验情况

针对4、7、15 kN/mm这3种刚度的弹性支撑，在风电机组装配厂内对风力发电机振动响应特性进行实验研究，以便得到不同刚度弹性支撑下风力发电机的振动表现情况。

3.1 测试设备

本次测试设备和用于测试的风力发电机的参数如表2所示。

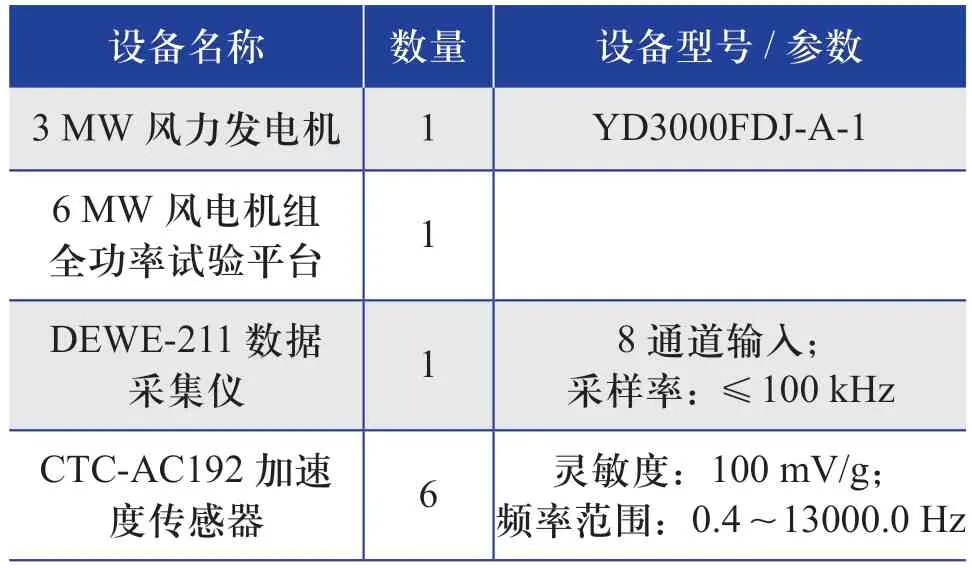
表2 测试设备和风力发电机参数Table 2 Parameters of test equipment and wind turbine generator

3.2 测点分布

测试过程中共使用6个CTC-AC192加速度传感器(编号分别为CH1～CH6)，分别布置在风力发电机驱动端和非驱动端轴承，其中每个轴承上各布置3个加速度传感器，分别采集水平、垂直和轴向3个方向的数据。加速度传感器测点位置分布的模型图和实物图分别如图3、图4所示。图中：CH1布置在风力发电机驱动端轴承水平方向；CH2布置在风力发电机驱动端轴承轴向方向；CH3布置在发电机驱动端轴承垂直方向；CH4布置在发电机非驱动端轴承水平方向；CH5布置在风力发电机非驱动端轴承轴向方向；CH6布置在风力发电机非驱动端轴承垂直方向。

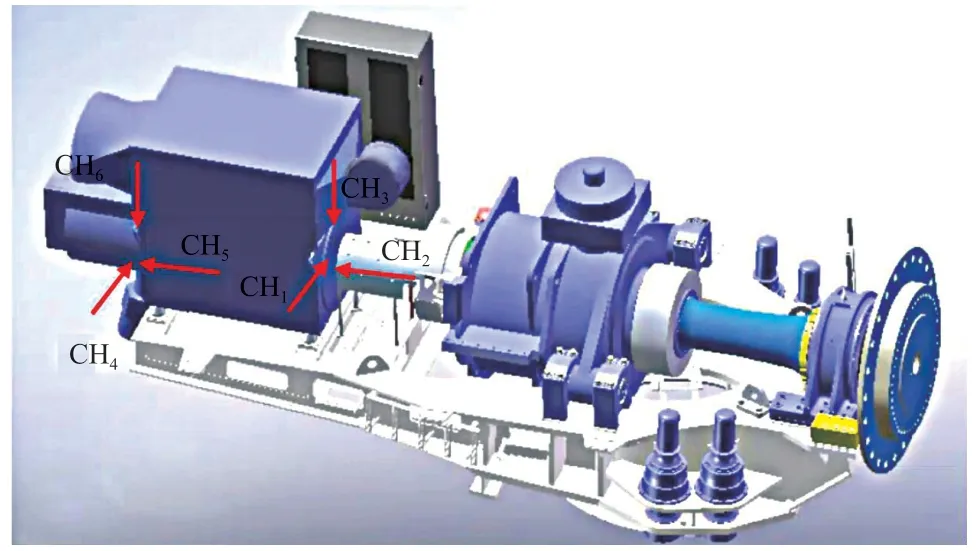
图3 加速度传感器测点位置分布的模型图Fig. 3 Model diagram of distribution of measurement points for acceleration sensors

图4 加速度传感器测点位置分布的实物图Fig. 4 Photos of distribution of measurement points of acceleration sensor

3.3 测试工况

在现场风电机组实际运行过程中，风电机组并网后的各项性能表现尤为重要，所以本文选择了风电机组并网后的18个转速及其对应的输出功率来研究风力发电机的振动响应情况。测试工况具体如表3所示。

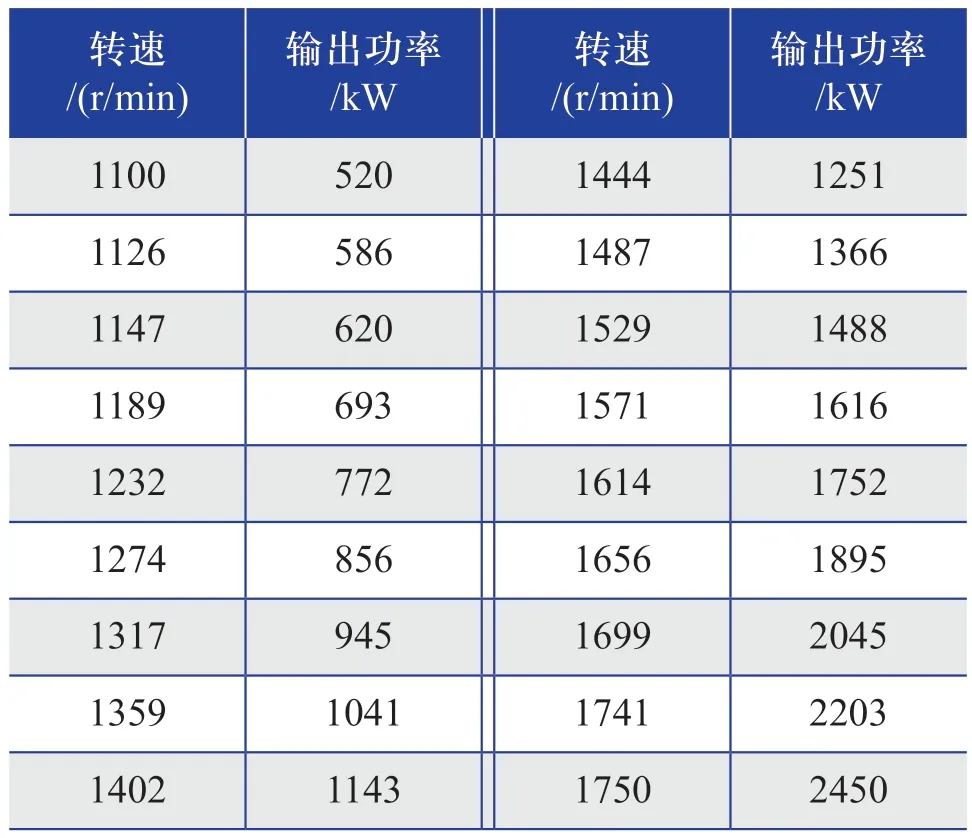
表3 测试工况Table 3 Test conditions

4 实验结果数据分析

4.1 速度有效值分析

针对不同刚度弹性支撑下风力发电机的振动响应特性，使用加速度传感器对风力发电机驱动端和非驱动端轴承在水平、垂直和轴向3个方向的加速度进行测试。通过分析计算得到，风力发电机驱动端和非驱动端轴承水平、垂直和轴向3个方向速度的有效值结果，分别如图5、图6所示。

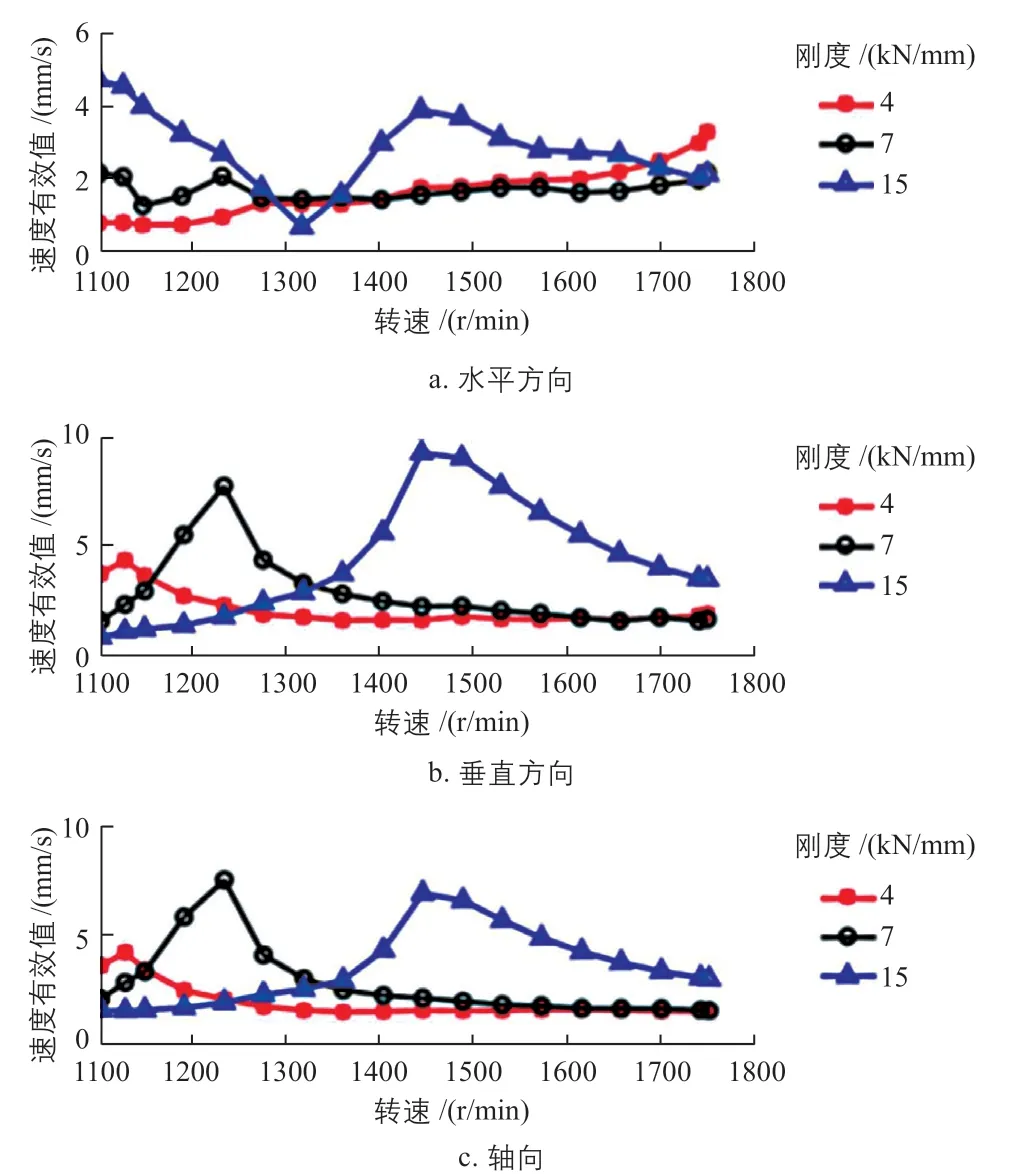
图5 风力发电机驱动端轴承3个方向速度的有效值Fig. 5 Effective values of speed in three directions at the bearing of wind turbine generator drive end

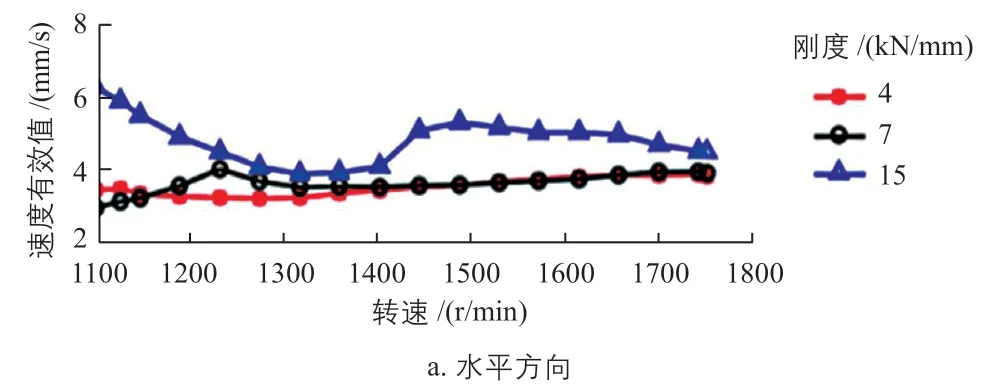
图6 风力发电机非驱动端轴承3个方向速度的有效值Fig. 6 Effective values of speeds in three directions at the bearing of wind turbine generator non drive end

通过观察图5和图6可以发现：在4、7、15 kN/mm这3种刚度的弹性支撑作用下，风力发电机驱动端和非驱动端的速度有效值均存在峰值，该峰值有对应的固定转速，风力发电机在该转速下出现共振，较好地反映了风力发电机在实际运行过程中的振动响应特性。

由于测试工况从风电机组并网后开始，所以本文的实验结果与仿真计算的第3阶模态的固有频率相对应。对实测得到的速度有效值峰值对应的发电机转速进行统计，计算该转速下的转频，即为实验得到的固有频率，并与仿真得到的固有频率结果进行对比，具体如表4所示。

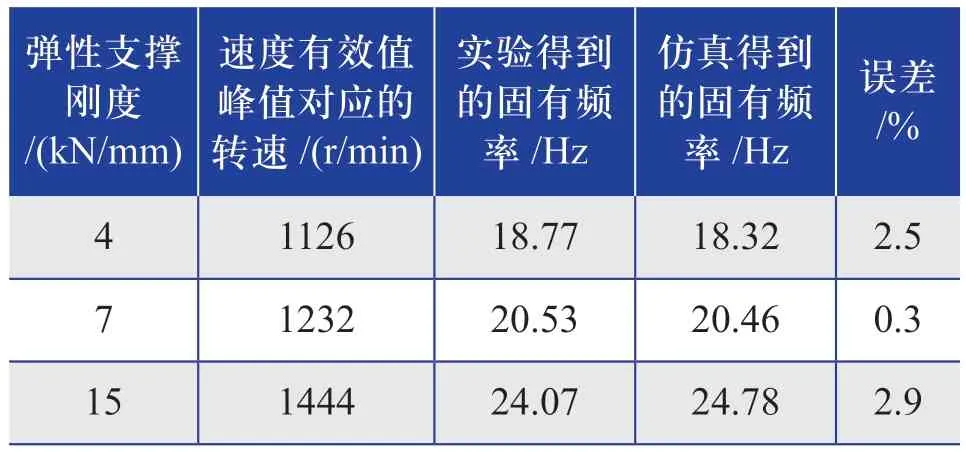
表4 实验得到的固有频率与仿真得到的固有频率对比Table 4 Comparison of natural frequencies obtained from experiment and simulation

由表4可知，在4、7、15 kN/mm这3种刚度弹性支撑下，风力发电机分别在转速为1126、1232、1444 r/min附近出现速度有效值峰值(即共振峰值)，通过其计算得到的固有频率与仿真得到的固有频率的误差均在3%以内。由此可知，不同刚度弹性支撑作用下风力发电机的振动响应特性的实验结果与仿真计算结果基本一致，验证了实验研究的有效性。

4.2 频谱分析

为了全面分析不同刚度弹性支撑作用下风力发电机的振动响应情况，对采集到的风力发电机驱动端和非驱动端的加速度信号进行频谱分析。由于本文研究的是风力发电机的动力学问题，其主要振动频率集中在1000 Hz以下，因此，首先通过对比观察选取了0～200 Hz的振动频率；然后，将同一刚度弹性支撑下不同转速的风力发电机振动频谱放在一起组成三维趋势图，并绘制二维频谱云图；最后，通过分析不同刚度弹性支撑下频谱云图的加速度峰值大小(即云图中颜色深浅)及其所占面积大小，来判断不同刚度弹性支撑下风力发电机振动响应的整体表现情况。

此处仅选取风力发电机驱动端和非驱动端的垂直方向作频谱分析，其他方向的频谱表现结果相似。

4.2.1 风力发电机驱动端垂直方向的频谱分析

4、7、15 kN/mm这3种刚度弹性支撑下风力发电机驱动端垂直方向的三维趋势图和频谱云图分别如图7～图9所示。

图7 4 kN/mm刚度弹性支撑下风力发电机驱动端垂直方向的三维趋势图和频谱云图Fig. 7 3D trend map and spectral cloud map of vertical direction of wind turbine generator drive end under 4 kN/mm stiffness elastic support

图8 7 kN/mm刚度弹性支撑下风力发电机驱动端垂直方向的三维趋势图和频谱云图Fig. 8 3D trend map and spectral cloud map of vertical direction of wind turbine generator drive end under 7 kN/mm stiffness elastic support

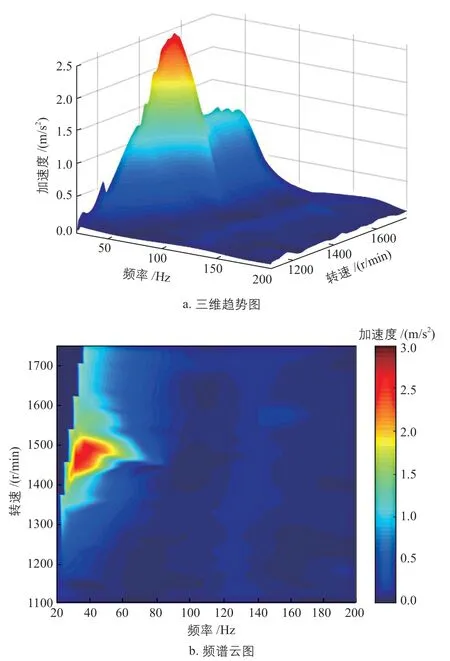
图9 15 kN/mm刚度弹性支撑下风力发电机驱动端垂直方向的三维趋势图和频谱云图Fig. 9 3D trend map and spectral cloud map of vertical direction of wind turbine generator drive end under 15 kN/mm stiffness elastic support

从图7～图9可知：风力发电机驱动端频谱云图中，4 kN/mm刚度弹性支撑下加速度峰值最小且所占面积最小，7 kN/mm刚度弹性支撑下加速度峰值较小，而15 kN/mm刚度弹性支撑下加速度峰值最大。由于4 kN/mm弹性支撑的刚度偏小，在风电机组整体设计时，对联轴器破坏较大，所以不能选用。综上，7 kN/mm刚度弹性支撑下风力发电机振动响应的整体表现更好。

4.2.2 风力发电机非驱动端垂直方向的频谱分析

4、7、15 kN/mm这3种刚度弹性支撑下风力发电机非驱动端垂直方向的三维趋势图和频谱云图分别如图10～图12所示。

图10 4 kN/mm刚度弹性支撑下风力发电机非驱动端垂直方向的三维趋势图和频谱云图Fig. 10 3D trend and spectral cloud diagram of vertical direction of non driving end of wind turbine generator under elastic support with stiffness of 4 kN/mm

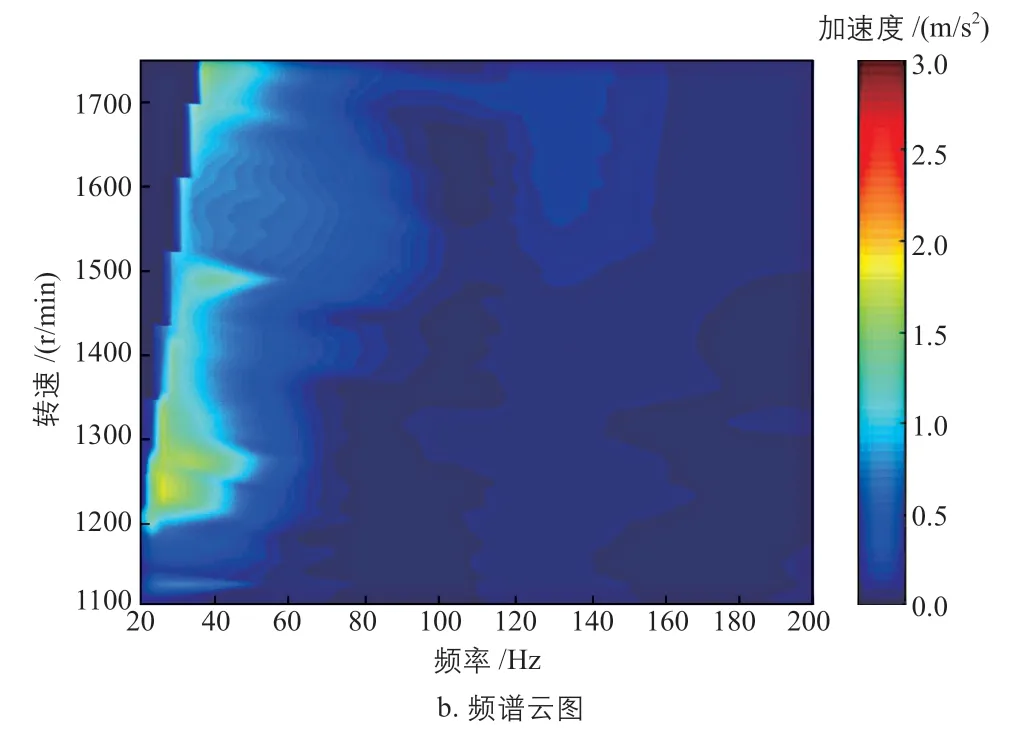
图11 7 kN/mm刚度弹性支撑下风力发电机非驱动端垂直方向的三维趋势图和频谱云图Fig. 11 3D trend and spectral cloud diagram of vertical direction of non driving end of wind turbine generator under elastic support with stiffness of 7 kN/mm

图12 15 kN/mm刚度弹性支撑下风力发电机非驱动端垂直方向的三维趋势图和频谱云图Fig. 12 3D trend and spectral cloud diagram of vertical direction of non driving end of wind turbine generator under elastic support with stiffness of 15 kN/mm

从图10～图12可以看出：在风力发电机非驱动端频谱云图中，4 kN/mm刚度弹性支撑下的加速度峰值最小且占有面积最小，7 kN/mm刚度弹性支撑下的其次，而15 kN/mm刚度弹性支

撑下的加速度峰值最大。由于4 kN/mm刚度弹性支撑在风电机组整体设计中的缺陷问题，所以7 kN/mm刚度弹性支撑下风力发电机振动响应的整体表现更好。

5 结论

本文针对4、7、15 kN/mm这3种刚度的弹性支撑，利用加速度传感器对某型号风力发电机的驱动端和非驱动端水平、垂直和轴向的振动响应特性进行了实验研究，并利用频谱云图分析风力发电机驱动端和非驱动端在垂直方向的振动响应下的表现，得到以下结论：

1)针对不同刚度弹性支撑下风力发电机的振动响应情况进行了理论建模和仿真计算，得到了4、7、15 kN/mm刚度弹性支撑下风力发电机前5阶振动模态对应的固有频率。

2) 通过对测试数据进行有效值和频谱分析可知，4、7、15 kN/mm这3种刚度弹性支撑下风力发电机分别在转速为1126、1232、1444 r/min附近出现速度有效值的共振峰值，由其得到的固有频率与仿真计算结果误差小于3%。

3)通过判断不同刚度弹性支撑下频谱云图的加速度峰值及其所占面积的大小发现，7 kN/mm刚度弹性支撑下风力发电机振动响应的整体表现更好。

本文的研究结果说明了不同刚度弹性支撑下风力发电机振动响应实验研究的有效性，频谱云图的峰值分析方法可为风力发电机弹性支撑选型提供分析依据，具有实际工程意义。