基于可观性分析的捷联惯导快速自对准方法

李晋斐,赵冬青,肖国锐,王栋民,杨朝永,赖路广

(信息工程大学 地理空间信息学院, 郑州 450001)

0 引言

捷联惯性导航系统(strapdown inertial navigation system,SINS)是一种自主式航位推算导航系统,无论是光纤惯导还是MEMS惯导,其提高精度的一个必要条件是获取准确的初始姿态,即进行初始对准。初始对准就是根据惯性器件的输出信息以及外界的参考信息,通过计算机平台的实时运算,不断更新从载体坐标系到导航坐标系的方向余弦矩阵[1]。初始对准误差是惯导系统主要误差源之一,对准精度和速度将直接影响导航系统的工作性能[2]。

捷联惯导系统经过粗对准和精对准2个阶段,粗对准特点是速度快、精度低,不涉及测量误差,只利用惯性器件的输出为下一步精对准提供一个满足要求的初始变换矩阵[3-4]。精对准阶段通过解算惯性器件的输出信息,准确地确定载体坐标系与导航坐标系之间的失准角,从而确定对准结束时刻的准确姿态变换矩阵[5]。通过将二者结合起来,在规定时间里满足系统精度要求。

Kalman滤波降阶模型可以消除不可观测状态量,降低模型阶数,简化滤波器[6-7]。文献[8]建立了10状态变量和以速度为量测信息的滤波模型,有效地估计了失准角精度,但未采取有效措施消除不可观测量的影响;文献[9]在此基础上将加速度计的输出和水平速度误差同时作为观测量,有限地提高了系统的可观测性,但随之而来的就是增加了计算量,并未完全消除不可观测量的影响;文献[10]同样采用以速度为量测信息的滤波模型,为了减小计算量,通过对10状态量模型降阶,从而完全消除不可观测量的影响,结果表明降阶处理对对准精度有明显效果,但在进行可观测性分析中,所用方法相当复杂。

针对上述问题,本文利用重力矢量与地球自转矢量进行解析粗对准,并在此基础上,对由解析计算得到的姿态矩阵进一步修正完成粗对准。由于比力测量与误差间有更少的积分步骤,可以更快地估计姿态和器件误差,故利用加速度计的输出作为量测信息,通过卡尔曼滤波进行精对准。通过可观测性分析,将不可观测状态量舍去得到降阶后的滤波方程,从而建立针对静基座条件下最简化的捷联惯导初始对准模型。

1 粗对准

粗对准是进行精对准的前提,要求短时间内得到一定精度的初始姿态矩阵,对于静基座条件下的初始对准,利用重力矢量与地球自转矢量通过解析法进行粗对准,然后进一步修正粗对准后的姿态矩阵,将粗对准得到的姿态角作为精对准的初始角度。

(1)

(2)

其中,L、g和ωie分别表示当地纬度、重力加速度和地球自转角速度的大小,上标T表示矩阵的转置。

解析式对准主要构建从载体系到导航系之间包含3个线性无关矢量的方程:

(3)

由式(1)和式(2)可知,g和ωie分别包含一个和两个非零分量,所以尽可能多地使用g将使误差角所包含的惯性器件误差更小,有利于模型的准确性[12],故选如下组合方式:

(4)

则有

(5)

2 精对准

精对准在粗对准结束后,通过对陀螺仪和加速度计引起的误差进行分析,利用惯性器件的输出信息代替水平速度作为量测信息建立相关误差模型,通过卡尔曼滤波不断地进行误差修正,以期获得更精确的初始变换矩阵。下面建立误差模型。

2.1 姿态误差分析

(6)

则失准角误差模型为[1]:

(7)

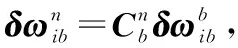
(8)

2.2 系统方程

选取东北天地理坐标系作为导航坐标系,在初始对准中将导航坐标系下加速度计的等效零偏和陀螺等效漂移当做随机常数扩充到状态模型中,即:

(9)

故由式(8)和式(9)可得捷联惯导系统静基座对准的系统方程:

(10)

2.3 量测方程

与陀螺误差对失准角的影响相比,加速度计误差的影响较小,采用基于加速度计的输出信息代替水平速度作为量测信息,更快地估计姿态信息。

(11)

(12)

(13)

则系统的量测方程为:

Z=HX+V

3 可观测性分析及模型简化

卡尔曼滤波器的估计效果依赖于系统的可观测性,因此确定完系统的系统方程和量测方程后,对系统进行可观测性分析是必要的,如果状态变量可观,则其滤波结果是收敛的。在静基座条件下,分析状态变量的可观测性,并根据结果去掉不可观测状态量,也就是对模型进行简化降阶,提高系统的稳定性,从而在未提高模型可观测性的条件下,消除不可观测状态量对整个系统精度和速度的影响。

首先通过判断系统可观测性矩阵是否满秩来测试系统的可观测性,静基座下的初始对准模型可近似为线性定常系统,其可观测性矩阵为[14]:

Q=[HHFHF2…HFn-1]T

(15)

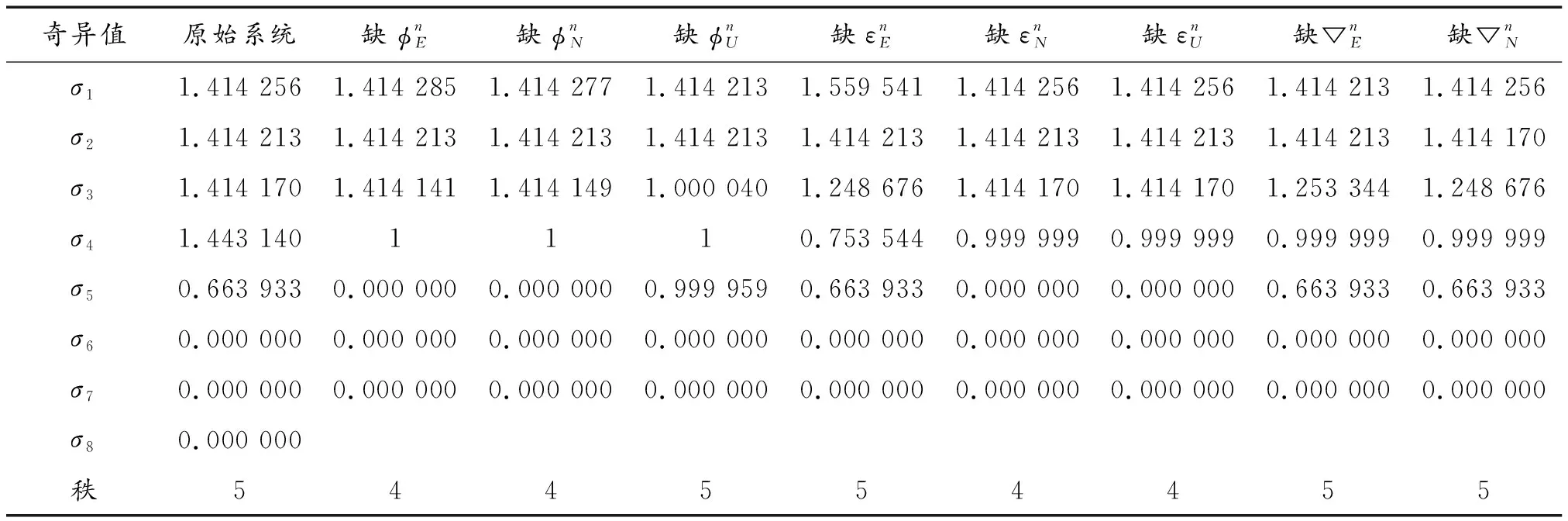
若rank(Q)=n,则说明系统完全可观测,通过计算得本文模型rank(Q)=5,说明系统有5个状态可观测,另外3个状态不可观测,但仅靠可观测阵的秩无法判断哪3个状态不可观测,所以需要进一步去定量分析不可观测状态。

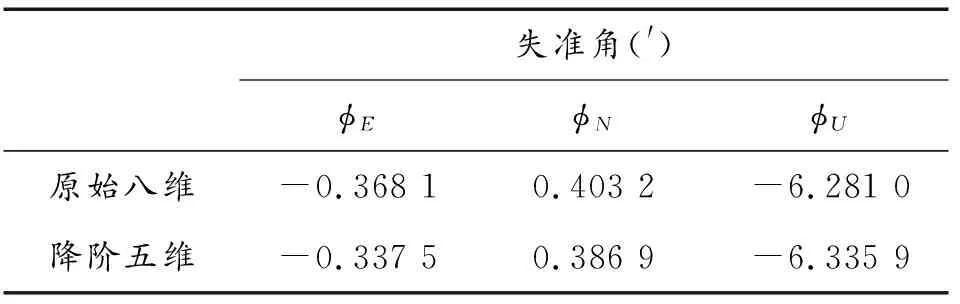
对于一个不完全可观测系统rank(Q)=r(r

根据上述分析,求取原始系统可观测阵的秩与奇异值,以及缺某状态量系统可观测阵的秩与奇异值,结果如表1所示。

(16)

表1 各系统可观测阵的秩与奇异值

4 实验分析

4.1 仿真比较

首先根据双矢量定姿方法进行解析粗对准,从文献[16]中得到失准角的理论极限精度计算方法,并与粗对准所得失准角结果做差,所得结果如表2所示。

通过表2,可以得出以下结论:

2) 通过与极限精度的对比可以发现,对于仿真的纯静基座条件下的捷联惯导初始对准问题,粗对准就可以提供一个完全满足条件的高精度初始姿态角。

表2 粗对准结果

粗对准结束后,进行两组精对准对比实验。第1组为以粗对准得到的姿态角为初始姿态角进行分析,第2组不以粗对准结果为初始姿态角,以所设初始失准角作为姿态角进行分析。以五维降阶模型为例进行精对准,经过计算,捷联惯导的姿态对准过程如图1所示。

图1 静基座捷联惯导姿态对准过程Fig.1 Attitude alignment process of static base strapdown inertial navigation

图1(a)为以粗对准结果为精对准初始姿态角的姿态对准曲线;图1(b)为未经粗对准,直接以初始姿态角为精对准初始姿态角的姿态对准曲线。从图1中可以看出,在精对准前进行粗对准,将使失准角处于小角度,能够使姿态角快速对准,减少对准时间;如果不进行粗对准,则初始失准角为大角度,需要一定时间进行收敛。经精对准后,其失准角结果如表3所示。

由表3可以看出,对于理想状态下的静基座初始对准问题,相比于直接进行精对准,先进行粗对准后再进行精对准,其方位失准角精度更高一些,水平失准角没有差别。

表3 精对准结果

其次,在进行粗对准后,针对可观性分析之后的滤波模型,分别对原始八维滤波模型与降阶五维滤波模型进行初始对准分析,2种情况下的对准过程如图2所示,为方便对比二者对准情况,红色直线为一条简单的参考直线。

图2(a)为原始八维滤波模型对准过程,图2(b)为降阶简化五维滤波模型对准过程,对准结果如表4所示。

表4 各模型得到的精对准结果

从图2和表4可以看出,2种模型的对准精度相当,这是因为降阶模型本质上未改变精对准模型的结构,其估计的极限精度与惯性元件零偏以及所处位置有关[17]。相比于原始八维滤波模型来说,简化降阶后的五维滤波模型的精度基本上没有损失,从水平姿态角来看,降阶五维滤波模型得到的结果略好于原始八维滤波模型;从方位姿态角来看,降阶五维滤波模型得到的结果略差于原始八维滤波模型。因此,可以看出五维降阶模型使得模型大大简化,在减少计算量的同时保证了对准精度,加快了运行速度,说明所提降阶模型是一种相对优化的静基座初始对准方法。

4.2 实测比较

图3(a)为原始八维滤波模型的精对准过程,图3(b)为降阶五维滤波模型的精对准过程。从图3中可以看出:

1) 相比于仿真实验,在实测实验环境下,捷联惯导并不是在纯静态条件下,存在一定的震荡,说明实际应用中环境复杂性对实验结果有一定的影响。

2) 对于光纤级别的惯导,由于其能够敏感到地球自转角速度,因此能够实现包括方位对准在内的快速自对准。

3) 对于水平姿态角,相比于原始八维滤波模型,降阶模型能够使姿态角更快收敛,并且对准曲线更为平滑,说明通过可观测性分析后的降阶模型不但能够减少计算量、加快运行速度,而且能够有效消除不可观测状态量对整个系统的影响。

5 结论

针对静基座条件下的捷联惯导初始对准问题展开研究,提出一种基于可观性分析的快速自对准方法,得到一种改进的完全可观测模型。分别进行仿真和实测实验,主要得到以下结论:通过与初始对准的极限精度相比,在静基座条件下,粗对准阶段就可以提供一个完全满足条件的高精度初始姿态角。降阶使得模型简化,从具体数据上看,2种模型对准精度相当,降阶模型在减少计算量的同时保证了对准精度,加快了运算速度。从实测数据中更能体现出降阶模型对于姿态角的收敛性,总体来说,本文的结果具有普遍性,是一种优化的静基座自对准方法。